一类共振问题周期解的新结果

王少敏， 杨存基

(大理学院 数学与计算机学院，云南 大理 671000)



一类共振问题周期解的新结果

王少敏， 杨存基

(大理学院 数学与计算机学院，云南 大理 671000)

主要目的是研究以下二阶系统

周期解；最小作用原理；二阶系统

引 言

考虑二阶系统

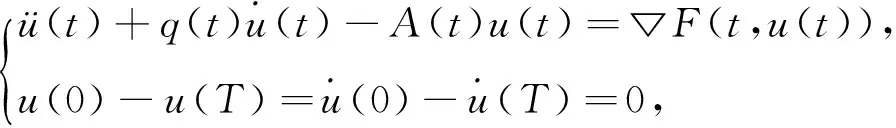
(1)

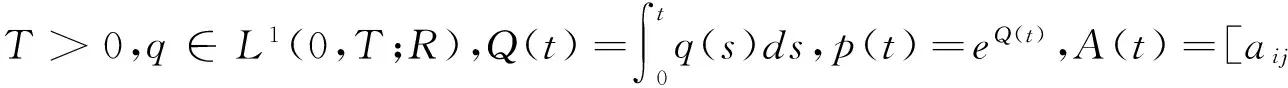
(A)：F(t,x)对于每个x∈RN关于t可测，对于a.e.t∈[0,T]关于x是连续可微的，存在a∈C(R+,R+),b∈L1(0,T;R+)使得

|F(t,x)|≤a(|x|)b(t)，|▽F(t,x)|≤a(|x|)b(t)x∈RN,a.e.t∈[0,T].

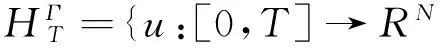
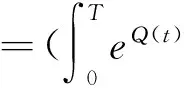
相应泛函

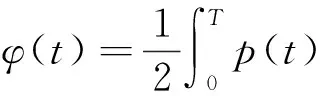
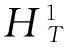
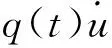
1 主要结果

定理1. 设F满足假设(A)且以下条件成立：

(i)若存在f,g∈L1(0,T;R+)及α∈[0,1)，使得

|▽F(t,x)|≤f(t)|x|α+g(t) ∀x∈RN, a.e.t∈[0,T]

(2)

(ii)存在h,w∈L1(0,T;R+)及β∈[0,2)且2α>β，使得

(A(t)x,x)≥h(t)|x|β+w(t) ∀(t,x)∈[0,T]×RN,

(3)

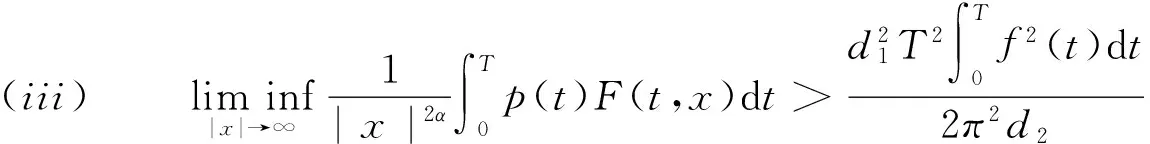
(4)

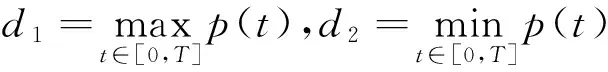
则问题(1)至少存在一个周期解.

定理2. 设F满足假设(A)，使得下面条件成立：

(i)若存在f,g∈L1(0,T;R+)及α∈[0,1)，使得

|▽F(t,x)|≤f(t)|x|α+g(t) ∀x∈RN,a.e.t∈[0,T]

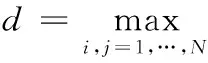
(5)

则问题(1)至少存在一个周期解.

2 定理的证明

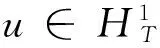
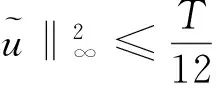
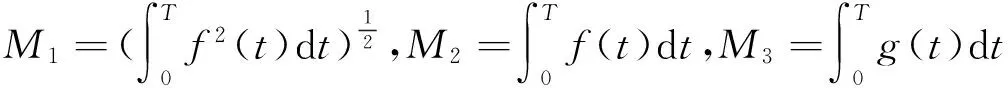
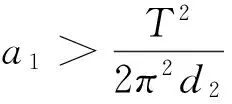
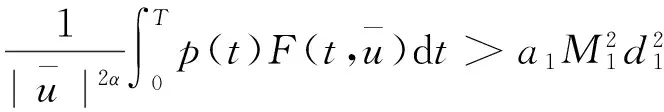
(6)

由(2)式及sobolev不等式得

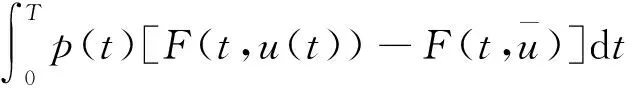
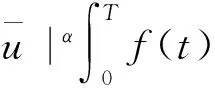
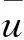
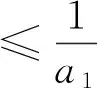
另一方面，有

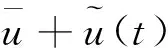
因此，我们有

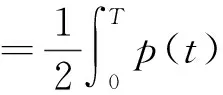
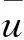
定理2的证明：

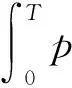
另一方面，由于3d2>2d1dNT2，有

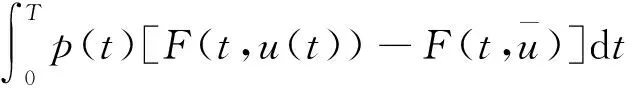
因此，我们有

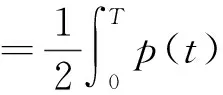
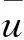
[1]WUX,CHENSHX,TENGKM.Onvariationalmethodsforaclassofdampedvibrationproblems[J]. Nonlinear Anal, 2008,68(1):1432-1441.

[2] FEI G H. On periodic solutions of superquadratic Hamiltonian systems[J]. Electon J Differential Equations, 2002,8:1-12.

[3] SCHECHTER M. Periodic solution of second order non-autonomous dynamical systems[J]. Bound Value Probl, 2006,1-9.

[4] WANG Z Y, ZHANG J H, ZHANG Z T. Periodic solutions of second order non-autonomous Hamiltonian systems with local superquadratic potential[J]. Nonlinear Anal, 2009,70:3672-3681.

[5] TAO Z L, TANG C L. Periodic and subharmonic solutions of second order Hamiltonian systems[J]. J Math Anal Appl, 2004, 293:435-445.

[6] TANG C L. Periodic solutions for non-autonomous second order systems with sublinear nonlinearity[J]. Proc Amer Math Soc， 1998,126:3263-3270.

[7] FARACI F. Multiple periodic solutions for second order systems with changing sign potential[J]. J Math Amal Appl, 2006,319:567-578.

[8] LI X, TANG X H. Existence of periodic solutions to second-order Hamiltonian systems with potential indefinite in sign[J]. Nonlinear Anal， 2008,69:3999-4011.

[9] MAWHIN J, WILLEM M. Critical point theory and hamiltonian systems[M]. New York: Springer-Verlag, 1989.

New Results of Periodic Solutions for a Class of Vibration Problem

WANG Shao-min, YANG Cun-ji

(Department of Mathematics and Computer, Dali University, Dali 671000, China)

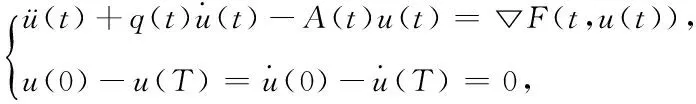
periodic solutions; the least action principle; second order systems

10.14182/J.cnki.1001-2443.2015.03.003

2014-10-08

国家自然科学基金项目(11261002)；云南省科技厅应用基础项目(2011FZ167).

王少敏(1975-)，女，云南大理，副教授，硕士，主要从事非线性分析的研究.

王少敏，杨存基.一类共振问题周期解的新结果[J].安徽师范学学报：自然科学版，2014，37(5)：228-231.

O

A

1001-2443(2015)03-0228-04

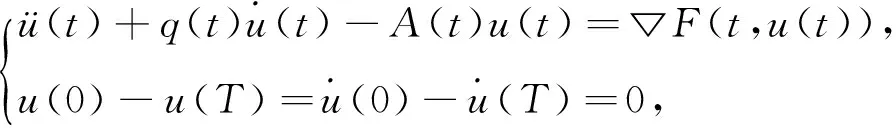
的周期解的存在性.在位势函数具有一定的有界性及A(t)是一个连续的N阶对称矩阵的条件下，通过使用最小作用原理获得了该系统的两个新的存在性定理.