深基坑变形多维度预测研究

贾淑玲

(中铁十八局集团第六工程有限公司，天津 300222)

随着城市地下空间技术的不断发展，深基坑工程的开挖深度愈来愈大，施工环境愈来愈复杂，施工安全问题也愈来愈突出。由开挖引起的变形是造成深基坑施工安全事故的重要原因，所以，必须严格控制施工过程中的变形并做出有效预测。由于岩土体材料的多相性、各向异性和非均质性，现有计算理论很难准确描述变形的影响因素。

人工神经网络是一种智能算法，具有较强的处理非线性问题的能力，在深基坑变形预测等方面得到了广泛应用。但大部分研究者只是针对变形数据本身做了分析预测，并没有考虑影响变形的各种因素。一旦预测出可能会出现超过报警值的情况，即使预报精度很高，由于无法得到造成这一危险的主要影响因素，对施工或设计甚至抢险决策作用并不大。所以必须在较准确预测出动态变形值的同时，还应分析各种主要影响因素，以便在可能出现危险的情况下提前采取相应的措施。本文考虑影响变形的多种因素，采用BP 神经网络方法建立深基坑变形预测模型，并通过实例验证预测模型的可行性，以满足设计与施工的需要。

1 影响深基坑变形的因素分析

(1)工程地质条件。因为工程地质条件的差别，支护结构受到后方土体的土压力差异很大。土压力是导致深基坑支护结构发生变形和位移的最直接原因，影响土压力大小的参数主要有土的重度、粘聚力和内摩擦角。

(2)水文地质条件。影响深基坑变形的水文地质条件主要包括地下水位的变化和土体的渗透系数两个因素。地下水位的变化会引起深基坑本身和周边土体的变形，且地下水位的变化一般不具有明显的规律性，在建立预测模型时要将其作为一个重要因素来考虑。随着地下水位的下降，软土会产生固结沉降，而土的固结和土体的渗透系数密切相关。

(3)深基坑空间尺寸。大量工程实践表明，随着基坑开挖尺寸的增加，支护结构的侧向位移、地表沉降及底面隆起量都会有不同程度的增加。对于某一特定深基坑工程而言，其平面尺寸不会随施工进程变化，但其开挖深度不断增加，深基坑变形也逐步增大。

(4)支护结构。影响深基坑变形的支护结构因素主要包括支护结构的类型、支撑的条件、结构刚度及支护结构入土深度。支护结构通常采用地下连续墙等支护方式，而且往往会在深基坑内设立内支撑。增加墙体厚度或者在一定范围内增加支护结构的入土深度可以减小深基坑的变形量，不过对于特定工程而言，墙厚和入土深度在设计阶段已经提前确定，施工阶段可以不作为能够改善变形的因素考虑。在施工阶段，最有效减小变形量的措施就是设置内支撑或土钉等措施，增大支撑的刚度可以有效减小深基坑的变形。

2 基于各影响因素的变形预测方法

针对深基坑开挖过程中的某一变形量，考虑其影响因素包括以下7 个参数:土的重度、土体粘聚力、土体内摩擦角、地下水位、渗透系数、深基坑开挖深度、内支撑层数，其向量分别记为γ、c、φ、w、K、H、N。在施工过程中可以获得以上各参数的统计值，同时也可以通过监测获得基坑的变形值。将上述参数的变化向量作为输入向量，将现场监测获得的变形值作为目标值，便可建立BP 神经网络。建立的BP 神经网络模型经训练收敛后，就可进行相关变形的预测。

(1)基坑开挖过程中，获取某一特定时刻开挖面以上所有土层重度的加权平均值、土体粘聚力的加权平均值、土体内摩擦角的加权平均值、地下水位、渗透系数的加权平均值、深基坑开挖深度、内支撑层数，即可获得一组训练样本;通过监测获得需要研究变形的实测数据，就得到了一组目标样本。将多个时刻的训练样本和目标值集中，即可获得多组样本，见表1。为了便于函数选择及计算，对训练样本和目标值进行归一化处理。

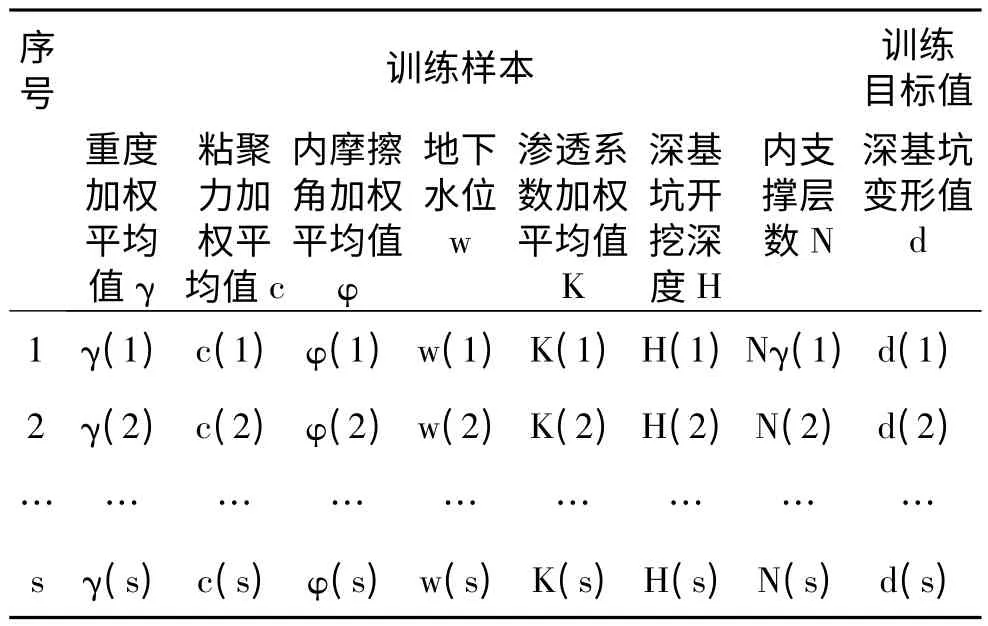
表1 网络训练样本、目标值

(2)进行神经网络模型设计，选择适当的算法，输入训练样本和目标值对网络进行训练，在达到规定的精度后训练停止，得到收敛的模型连接强度。

(3)使用收敛的模型连接强度，将后续某一时刻的影响参数序列γ(s+1)、c(s+1)、φ(s+1)、w(s+1)、K(s+1)、H(s+1)、N(s +1)的归一化数据作为网络输入，使用训练好的网络便可预测出深基坑变形值d(s+1)。

(4)为了增加预测模型的精度，在获取新的监测数据后，将新数据作为样本加入到模型中对模型进行重新训练，模型收敛后可用于后续变形的预测。

3 沉降预测的BP 模型

深基坑周边建筑物沉降变形、深基坑范围内平面位移点的水平位移、开挖区域土体位移孔位移、测斜孔最大位移等都可作为训练目标值建立BP 神经网络预测模型，并对相应变形进行动态预测。本文以周边建筑物沉降变形为例介绍BP 神经网络预测模型。

网络的隐含层层数、输入层、隐含层及输出层之间的传递函数类型、隐含层节点数对模型的预测精度影响较大。如果神经元数目不太多，预测模型只需一个隐含层便能获得比较好的预测效果。模型建立时一个连续等时距的土的重度、土体粘聚力、土体内摩擦角、地下水位、渗透系数、深基坑开挖深度、内支撑层数的归一化数值作为输入层的7 个节点，深基坑周边的测点沉降值作为输出层一个节点，隐含层节点数取为n=8～30 并逐个进行检验，重点考察网络预测误差、网络收敛速度等指标。网络结构取7-n-1(n 待定)，网络结构如图1 所示。

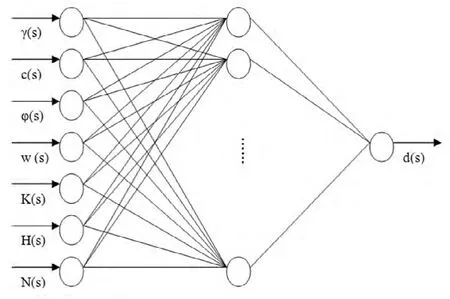
图1 变形发展预测的BP 网络结构

经过检验，采用logsig 函数为传递函数、Levenberg-Marquardt 算法为训练函数可以满足建模的要求，所有模型采用logsig 函数及Levenberg-Marquardt 算法，利用MATLAB 神经网络工具箱编制程序进行计算。

4 基于深基坑变形影响因素的深基坑工程施工期变形预测

4.1 工程概况

某地铁车站为地铁2 号线和3 号线换乘站，上面为3 号线，下面为2 号线。2 号线、3 号线同步施工，在2、3 号换乘节点施做临时封堵桩，将两站分做两个条形基坑，2 号线基坑地下3 层，3 号线基坑地下2 层，采用明挖法施工，基坑开挖深度12～29.5m，基坑地下一层南、北侧采用土钉墙支护，换乘节点处3 号线基坑采用桩+锚支护，地下二层采用土钉墙支护，2 号线基坑地下二、三层采用桩+内支撑支护。结合测区状况及地面建筑物、管线状况和施工顺序，布设较密集的监测点并设置监测主断面进行全面监测。

4.2 建筑物沉降变形预测

以沉降变形观测点C013 为例，取前20 个监测周期实测数据对应的主要影响因素数据，作为训练样本建立BP 神经网络预测模型，样本数据见表2。此时，在建立的预测模型中，当隐含层节点数在8～30 之间变化而其它因素保持不变，隐含层节点数为14 时，模型的网络预测误差最小，收敛速度也很快。

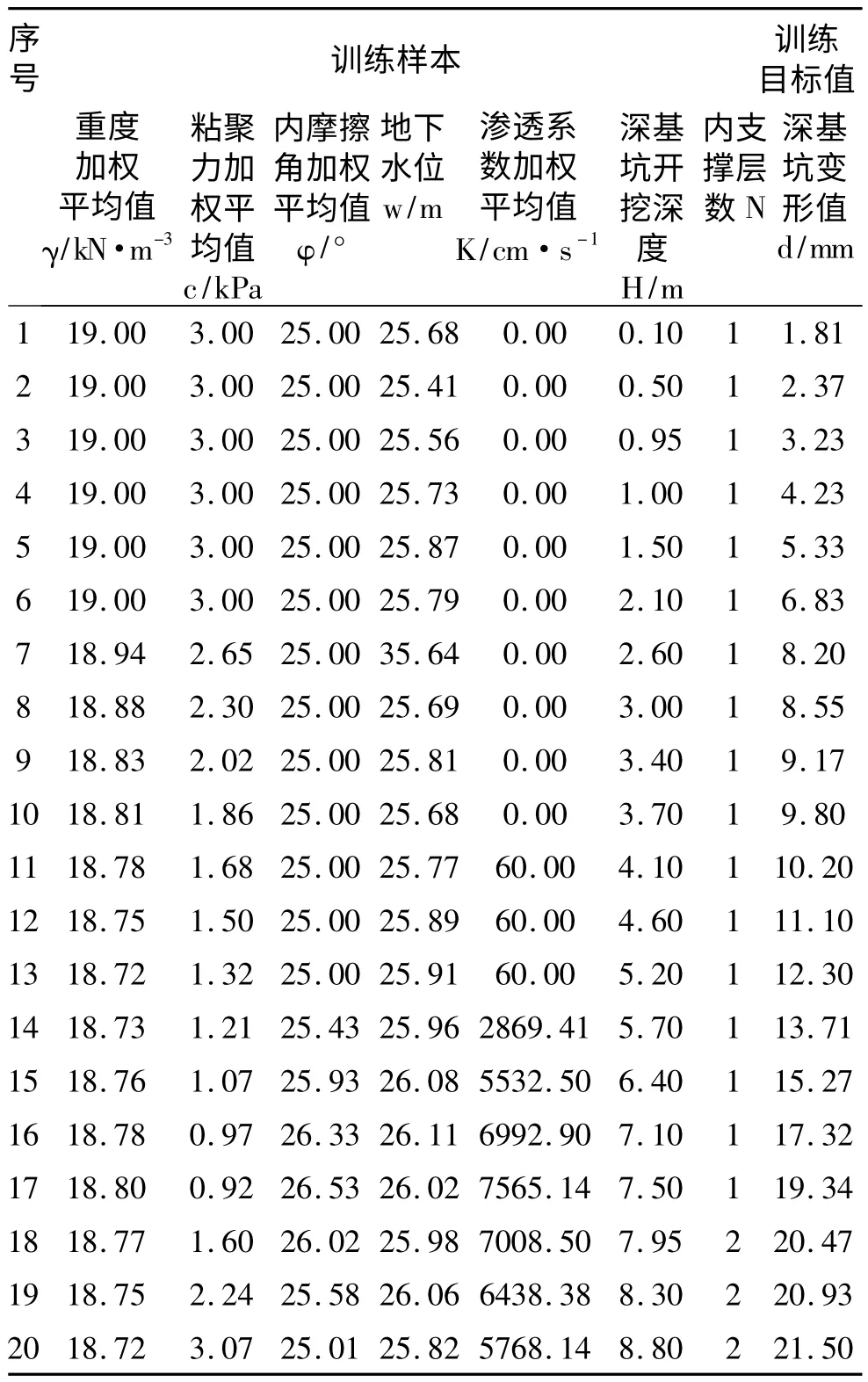
表2 BP 神经网络建模用样本数据

因为编好程序的计算工作都由计算机来完成，并且模型收敛速度都较快，所以在每次模型建立时都对隐含层节点数进行优选，从而保证预测的精度。从误差曲线图2 可以看到，网络收敛速度较快，说明建立的模型及选取的参数质量较好。

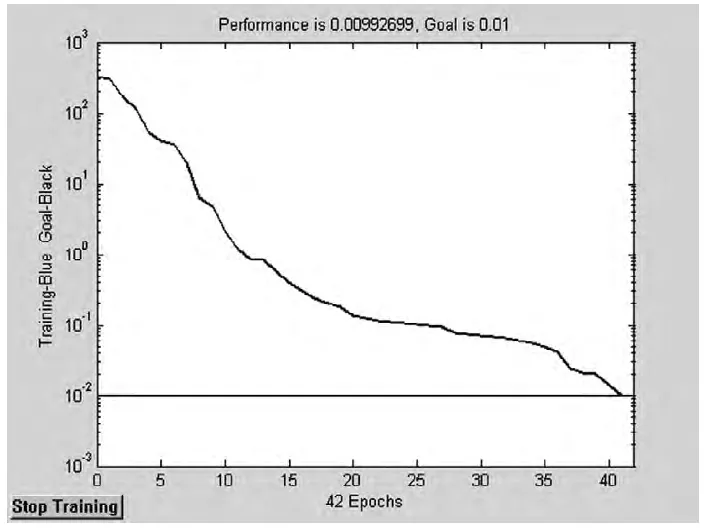
图2 网络预测误差曲线

在建立BP 神经网络模型并采用表2 所列训练样本及目标样本进行训练并收敛后，将表3 所列的各组后续时刻的各项参数作为输入样本输入到训练好的网络模型中，便可得到对应的网络输出。

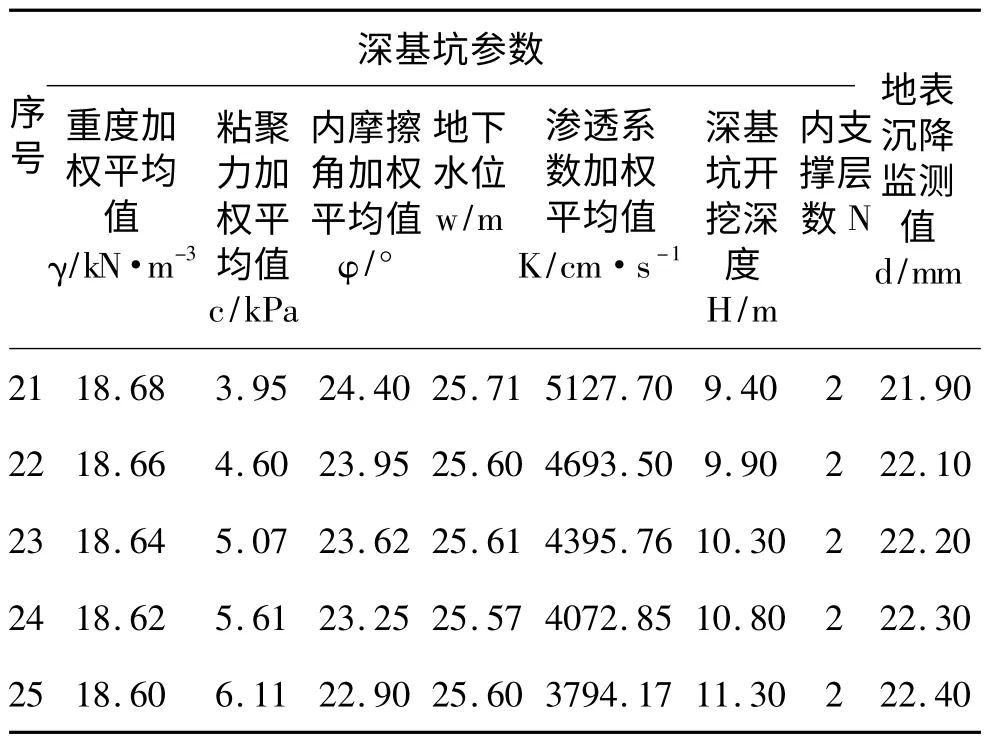
表3 地表沉降BP 神经网络预测

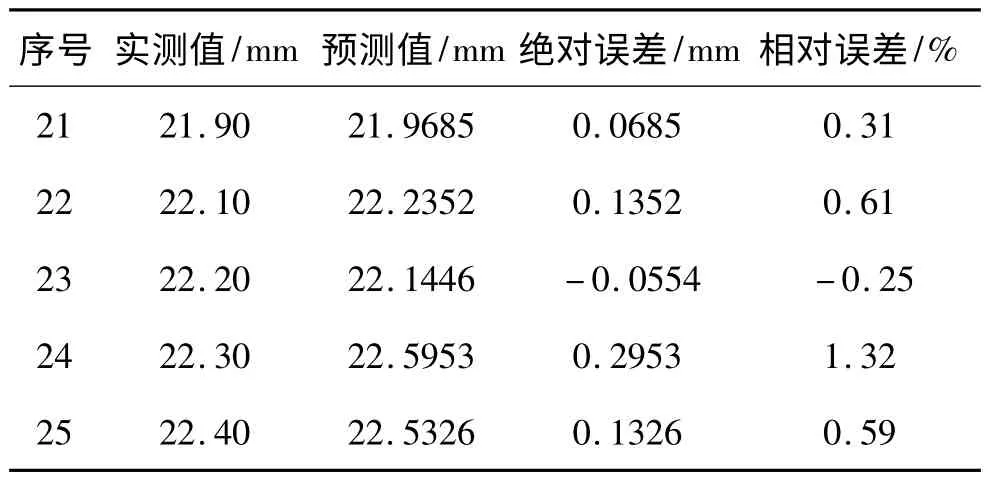
表4 网络预测值及误差分析

预测值与现场监测值及其预测误差均列入表4中。由表4 可见，模型的预测误差较小，相对误差绝对值在1%以内，最大误差也仅1.32%，对于深基坑的变形来说，这样的预测误差值是很理想的，完全满足工程施工及设计的要求。

5 结束语

本文的研究结果表明，结合地质勘查资料、设计文件等，以各施工时段的土的重度、土体粘聚力、土体内摩擦角、地下水位、渗透系数、深基坑开挖深度、内支撑层数等7 个因素值为训练样本，实际观测的深基坑变形值为目标值建立的开挖变形预测BP 网络模型，预测误差非常小，模型精度很高，可以对深基坑施工或设计提供理论参考和支持。

［1］张彬，李洋，于相连，等.地铁深基坑安全优化有限元模拟［J］.辽宁工程技术大学学报(自然科学版)，2015，34(1):21-25.

［2］胡康俊，丰土根，张福海，等.深基坑开挖坑底隆起影响因素有限元分析［J］.施工技术，2014，43(22):116-119.

［3］熊孝波，桂国庆，郑明新，等.基于免疫RBF 神经网络的深基坑施工变形预测［J］.岩土力学，2008，29(S1):598-602.

［4］刘贺，张弘强，刘斌.基于粒子群优化神经网络算法的深基坑变形预测方法［J］.吉林大学学报(地球科学版)，2014，44(5):1609-1614.

［5］马建林.土力学［M］.第三版.北京:中国铁道出版社，2011:195-199.