考虑车辆机械惯性的跟驰模型及其数值模拟分析

周 桐，李雨宣，杨智勇，孙棣华

(1．重庆工程职业技术学院 信息工程学院，重庆402260;2．重庆大学 自动化学院，重庆400044)

0 引言

城市道路交通问题日趋严峻，而驾驶行为与交通拥堵关系密切． 为了认知驾驶行为与交通拥堵之间的关系，众多学者提出了很多交通流模型［1-3］．Bando 等［4］、Helbing 等［5］、姜锐等［6］根据一些典型的交通现象，提出了一系列具有代表性的模型，具有较好模拟效果．但上述模型仅考虑了最邻近车辆的运动状态信息． 随着智能交通系统的发展，车辆信息获取的条件改善，有利于获取道路上其它车辆的信息，为准确地认识驾驶行为与交通拥堵的关系奠定了基础．基于典型的FVD 模型［6］，已有学者通过考虑多辆前导车的相关信息，提出了一系列的扩展模型．其中，既有针对车头距的协同驾驶模型［7］和针对多速度差的跟驰模型［8］，也有综合两者信息的跟驰模型［9-11］． 研究表明，考虑多车作用关系的驾驶行为对拥堵具有抑制作用．

上述模型均能较好地提高车流的稳定性和描述实际的交通现象，却未考虑车辆系统中机械惯性效应对交通流的影响，导致在模拟车队静止启动时，头车的加速度出现瞬间跳跃现象，而这种现象在实际的车流运行中是不可能存在的． 由于车辆机械惯性阻碍车辆运动状态发生变化，导致车辆加速至最优状态需要一段时间，不能瞬间变化．因此，车辆的机械惯性对车辆的驾驶行为具有重要的影响．目前，考虑车辆机械惯性效应的跟驰模型鲜见报道，因此，笔者在FVD 模型的基础上，考虑车辆机械惯性对驾驶行为的影响，提出一种新的跟驰模型，并通过车队静止启动过程和车辆动态演化数值仿真验证了改进模型的合理性和必要性．

1 跟驰模型

1995 年，Bando 等［4］在经典跟驰模型基础上提出优化速度(OV)模型，其运动学方程为

式中:vj(t)，xj(t)，Δxj(t)和adesiredj(t)分别表示第j 辆车在t 时刻的速度、位置、车头间距和期望加速度;k 为司机的敏感系数;V(·)是与Δxj(t)相关的优化速度函数． 应用该模型可以模拟实际交通中诸如时停时走，交通迟滞、交通阻塞的传播等非线性交通现象．

1998 年，Helbing 和Tilch 采用实测数据对OV 模型进行了参数标定，发现该模型存在着过高加速度以及与现实不符的减速度，因此，通过引

式中:Δvj=vj+1-vj为车辆的相对速度;H(-Δvj)是Heaviside 阶梯函数;λ 是对最邻近前车相对速度的反应系数． 尽管该模型避免了OV 模型中出现过高加速度的情况，然而却出现了延迟时间较长的新问题，同时也不能解释Treiber 等［5］指出跟驰车辆速度比前车小很多时，尽管两者距离小于安全距离，跟驰车辆也不会减速的正速度差现象．因此2001 年，姜锐等人基于GF 模型提出了全速度差(FVD)模型，其运动方程［6］:

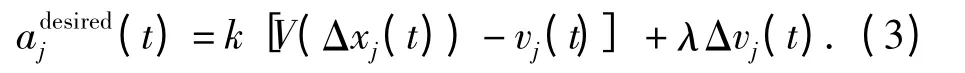
模型中参数k 和λ 的物理意义与文献［5］一致．此后，在FVD 的基础上，一系列扩展模型被相继提出［7-10］．

上述跟驰模型对交通流具有致稳的作用，也能在一定程度上描述驾驶行为与交通拥堵的关系，但这些模型未考虑车辆自身的机械惯性对车流的影响．在实际车辆控制中，驾驶员首先感知车辆周围的环境信息，然后经过驾驶员大脑分析、处理和决策，给定一个期望的加速度控制指令，然后通过手和脚作用于车辆使之加速还是减速，在作用过程中由于受车辆机械惯性的影响，使得给定的期望加速度发生了一定的改变，即为实际的加速度．因此，基于FVD 模型，笔者提出一个考虑车辆机械惯性效应的跟驰模型，其形式为

式中:lc为车辆长度，在数值仿真中lc=5 m．其它参数值V1，V2，C1和C2分别为6． 75 m/s，7． 91 m/s，0．13 m-1，1．57．

2 稳定性分析

为了方便后续模型的稳定性分析，笔者从控制角度对模型(4)进行了重写:

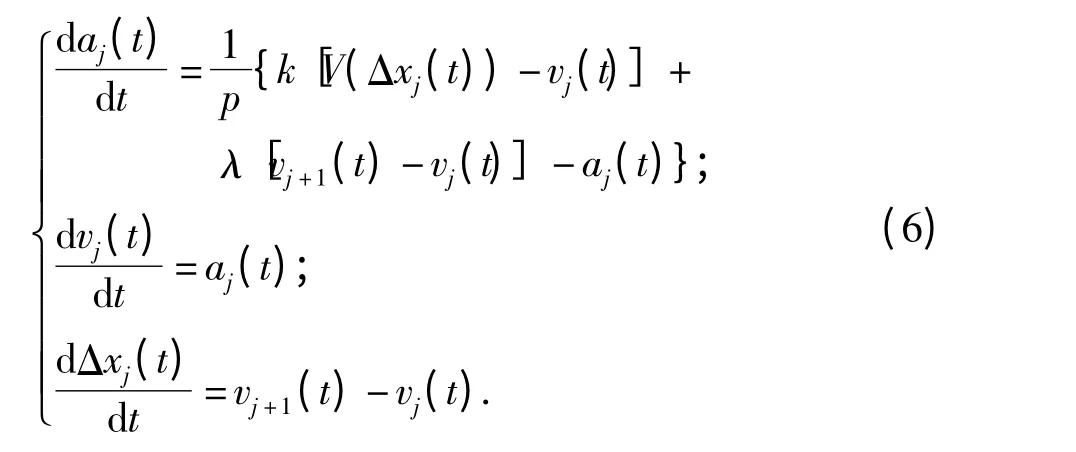
假设车队头车以恒定的速度v0运行，则跟随车的稳定状态为

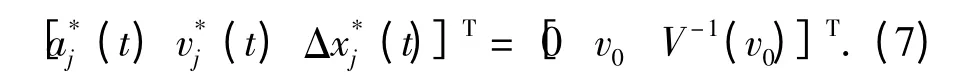
将模型(6)在稳定状态式(7)周围线性化，得到了交通系统(6)在稳定状态附近的扰动模型描述如下:

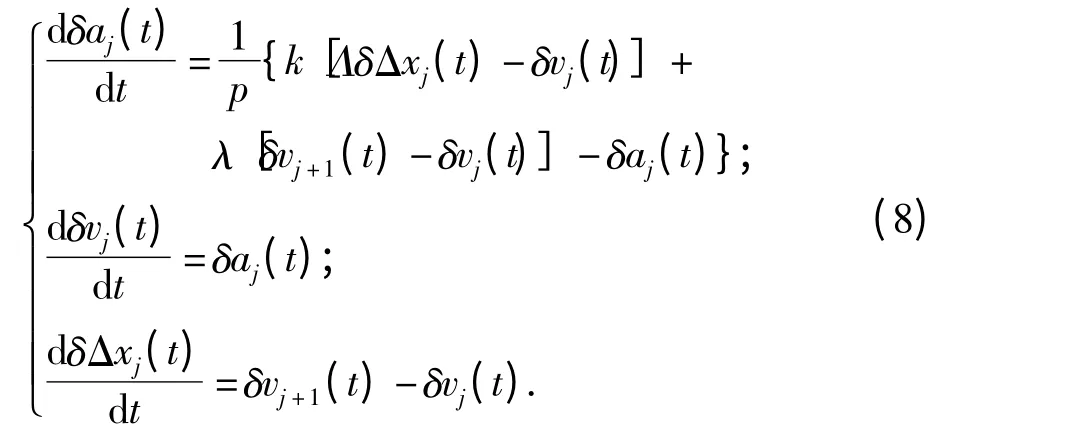
则模型(6)在稳定状态附近的状态空间表达式为:

其中设定τ=1/p，vj(t)=δvj(t)+v0，Δxj(t)=δxj(t)+h0，Λ 为优化速度函数在Δxj(t)=V-1(v0)处的斜率，

考虑跟驰模型中连续两辆车即第j+1 辆车的速度与第j 辆车的速度关系，从频域角度来看，模型(6)可以进一步改写成

Vj(s)=G(s)·Vj+1(s)． (10)

式中:Vj(s)=L(δvj+1(t));Vj+1(s)=L(δvj+1(t))，L(·)代表拉普拉斯变换，这样传递函数G(s)为:

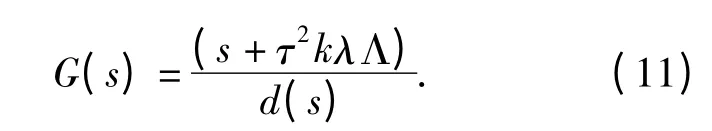
其中，d(s)=τλ(s3+τs2+(τk+τλ)s+τkΛ)．

基于Konishi 等［1］提出的系统稳定性分析方法，给出了一个不出现交通拥堵现象的引理．

引理1 系统(6)不会出现拥堵现象必须满足两个条件:一是特征多项式d(s)是稳定的;二是传递函数G(s)的H∞范数小于等于1，即

根据引理1，对式(11)进行求解得到了交通系统保持稳定的条件

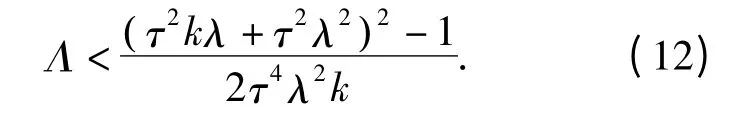
从式(12)中可以看出，系统随着τ 的减小，系统的性能越好． 图1 表示交通系统传递函数G(s)的增益曲线|G(jw)|． 从图中可以看出:当τ=1，0．5，0．4 时，增益曲线|G(jw)|出现一个峰值，但峰值过后衰减速度较快;而当τ =0．25 时，增益曲线|G(jw)|没有出现峰值，但峰值过后衰减速度较慢．可见在笔者提出的模型中在其它参数不变的情况下，随着驾驶员对车辆机械惯性关注程度的增加，有利于改善车辆控制系统的性能．因此，车辆机械惯性对驾驶行为与交通拥堵的关系起着重要作用．

图1 系统传递函数G(s)的增益曲线Fig．1 The gain curve of G(s)

3 数值仿真

笔者通过车队静止启动仿真和车辆动态演化仿真对新模型的动态性能进行验证．

3．1 启动过程对比仿真

下面研究笔者提出的模型在黄灯转向绿灯时交通信号环境下的车辆启动情况，并检验新模型的动态特性． 模拟静止车队的启动过程:在t ＜0时，交通信号为红灯，10 辆车排成一队，每辆车的初始位置为xn(0)=(n -1)d，其中n =1，2，…，10，d =7．4 m，所有车辆初始状态都处于静止状态，即vn(0)=0，(n =1，2，…，10);在t =0 时，黄灯转绿，车辆开始启动．其它边界条件:对于头车n=10，最优速度函数为V10(∞)=14．66 m·s-1，对于跟随车，有Vn(7．4)=0，(n =1，2，…，9)．为了与FVD 模型作对比实验，设置两个模型的参数相同．在模拟中，选取λ =0．5 和k =0．41 s-1，并选取Helbing 和Tilch 用实测数据进行参数辨识得到的OV 函数(5)式，模拟结果如图2 和图3 所示．图2 给出了车队静止启动时新模型与FVD 模型中头车的加速度分布曲线，从图2 中可见FVD模型中头车的加速度出现瞬间跳跃的现象，而新模型中头车加速度没有出现这种现象，而是缓慢变化升至最大值，这符合实际的交通规律．

图2 头车的加速度分布曲线Fig．2 The acceleration distribution curves of unobstructed leading vehicle in two models

图3 为两个模型中车辆启动过程的速度分布曲线．从图中可以看出，FVD 模型车队启动的延迟时间较新模型的启动时间要短．这是FVD 模型由于没有考虑车辆自身机械惯性的影响，所以到达稳态速度的时间较快，而笔者设计的模型由于惯性延迟的作用，到达稳定速度时间要慢．同时，可以从图中可以看出，FVD 模型中速度的斜率较新模型中的斜率大，说明驾驶员期望加速度要大于实际的加速度．根据上述分析，笔者提出的模型在启动过程中，能够克服车队静止启动时头车加速度瞬间跳跃的现象，同时车辆速度加速至最优速度的时间要长于FVD 模型的结果．

3．2 演化过程对比仿真

为了更加直观地分析车辆机械惯性对车流稳定性的作用，现利用数值模拟以验证笔者提出的模型演化特性．设周期边界条件为:L =1 500 m，车辆数N = 100，对头车施加小扰动x1(0)=L/N+1下，敏感系数选取a =0．41 s-1，其它参数λ=0．5，τ=0．5．车辆的初始条件如下:

图3 车辆启动过程的速度分布Fig．3 The velocity distribution of vehicles starting process

x1(0)=1 m，xn(0)=(n-1)L/N(n=2，3，…，N)，vn(0)=V(L/N)(n=1，2，…，N)．

图4 和图5 为FVD 模型和新模型在t=500 s和t=1 200 s 处的速度分布曲线图． 在图中，当p=0时，新模型退化成FVD 模型． 从模拟结果中可以得知:在两个模型中，由于不能满足稳定性条件(12)，这样，初始小扰动随着车队的向后传播放大，最终引起时走时停的交通阻塞现象．但值得注意的是，当t=500 s 时，发现新模型的速度波动幅度较FVD 模型的结果要小，即由于机械惯性的作用，导致实际加速度比期望加速度要小，因此，新模型中的实际速度是小于FVD 模型中期望速度的．而且由于惯性延迟作用导致新模型的速度波动的时间较FVD 模型的结果要相对滞后一小段时间．而当t=1 200 s，由于两个模型中车辆已经出现时走时停现象，所以速度波动的幅度几乎一致，但是新模型的速度波动时间还是滞后于FVD 模型模拟结果的时间．这足以说明在FVD 模型中考虑了车辆机械惯性能更加真实地描述实际的驾驶行为与交通拥堵关系．

图4 时步t=500 s 的车辆速度分布Fig．4 The snapshots of the velocities of two models at t=500 s

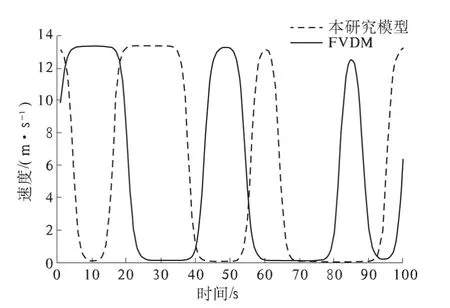
图5 时步t=1 200 s 的车辆速度分布Fig．5 The snapshots of the velocities of two models at t=1 200 s

4 结论

笔者在FVD 模型的基础上，考虑车辆机械惯性的作用，提出了一个新的跟驰模型．通过系统稳定性分析，得到了系统保持稳定的条件．仿真结果表明:与FVD 模型相比，考虑车辆机械惯性的作用能够克服FVD 模型中车队静止启动头车的加速度出现瞬间跳跃现象;同时，新模型较FVD 模型能够更加真实地模拟实际交通现象，从而验证了模型的性能优越性和合理性． 笔者主要研究单车道限制超车跟驰模型的交通特性，下一步将在笔者提出的模型中引入换道规则，研究双车道车流的演化特性．

［1］ ZHOU Tong，SUN Di-hua，LI Hua-min，et al．A new coupled map car-following model considering drivers’steady desired speed［J］． Chinese Physics B，2014，23(5):41 -45．

［2］ 孙棣华，周桐，刘卫宁，等．考虑最近邻前车综合信息的反馈控制跟驰模型［J］． 物理学报，2013，62(17):170503 -170508．

［3］ GUPTA A K，SHARMA S． Analysis of a modified two-lane lattice model by considering the density difference effect［J］． Communications in Nonlinear Science and Numerical Simulation，2014，19 (5):1600-1610．

［4］ BANDO M，HASEBE K，NAKAYAMA A，et al．Dynamical model of traffic congestion and numerical simulation［J］． Physical Review E，1995，51(2):1035-1042．

［5］ HELBING D，TILCH B． Generalized force model of traffic dynamics［J］． Physical Review E，1998，58(1):133 -138．

［6］ JIANG Rui，WU Qing-song，ZHU Zhi-jun．Full velocity difference model for a car following theory［J］．Physical Review E，2001，64(1):017101．

［7］ 孙棣华，李永福，田川．基于多前车位置及速度差信息的车辆跟驰模型［J］． 系统工程理论与实践，2010，30(7):1326 -1332．

［8］ 王涛，高自友，赵小梅．多速度差模型及稳定性分析［J］．物理学报，2006，55(2):634 -640．

［9］ TIAN Jun-fang，JIA Bin，LI Xin-gang，et al． A new car-following model considering velocity anticipation［J］．Chinese Physics B，2010，19(1):010511．

［10］ PENG Guang-han，CAI Xin-hua．，LIU Chang-qing，et al． Optimal velocity difference model for a car-following theory，Physics letters A，2011，375(45):3973 -3977．

［11］廖孝勇，孙棣华，彭光含，等． 双前导车信息对交通流稳定性影响的分析［J］．重庆大学学报，2011，34(8):195 -199．