求解极大相关问题的对偶方法❋

李美然, 刘新国(中国海洋大学数学科学学院，山东 青岛 266100)



求解极大相关问题的对偶方法❋

李美然, 刘新国
(中国海洋大学数学科学学院，山东 青岛 266100)

多组变量间的极大相关问题(MCP)有重要统计应用。目前已有的求解MCP的算法都不能保证获得MCP的全局解。本文通过求解MCP的对偶问题，给出了一种改进的Lagrange对偶方法。最后，数值实验结果说明了新方法能提高收敛到全局解的可能性。

极大相关问题；多元特征值问题；Lagrange对偶；强对偶；全局解；收敛性

0 引言

多组变量的极大相关问题(Maximal correlation problem,MCP)是经典的典型相关分析(Canonical correlation analysis,CCA)[1-2]的自然推广，已被广泛用于聚类分析、数据分析、模式识别、主成份分析以及动力系统的稳定性分析等问题中。

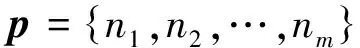
这里，Aii∈Rni×ni，求解

(1)

其中

使用Lagrange乘子法可知，x∈Σm为MCP(1)的解的必要条件为：存在实数λ1,…,λm，使得：

Ax=Λx；

Λ=diag(λ1In1,…,λmInm)。

(2)

式(2)称为多元特征值问题(MEP)[3]。若(Λ,x)满足(2)，则称(Λ,x)为MEP(2)的一个解。Chu和Watterson[3]。

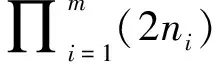
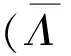
注意到(1)是一类具约束的非线性最优化问题。AVM方法是常用的坐标下降法[12-13]的自然推广。自然地,可以考虑应用其它的最优化方法求解MCP(1)。本文分析求解(1)的对偶方法。本文以下内容组织如下。在第二节，给出(1)的对偶形式,并使用对偶方法求解(1)。由于m≥3时(1)与其Lagrange对偶问题之间不是强对偶的，因此，给出了一种改进的对偶方法；最后，关于对偶方法做了大量的数值实验，结果表明，对偶方法能有效地获得MCP的全局解。

1 对偶方法

首先，将给出MCP(1)的Lagrange对偶问题。注意MCP(1)等价于下述最优化问题(见Sun[6])：

(3)

易知，(3)的Lagrange对偶问题为：

(4)

这里，Λ=diag(λ1I1,…,λmIm)，若令Fi=diag(0,…,0,Ini,0,…,0)∈Rn×n，则(4)可以改写为：

(5)

显然，(5)是标准的半定规划问题，可以使用内点法求解，且已有较好的软件包，例如，Sedumi[14]，SDSP[15]。

(Λ*-A)x=0。

(6)

如果(6)存在解x*∈Σm，那么，由Hanafi和Ten Berge[8]的结果可知，x*就是MCP(1)的一个全局解，此时(5)与(3)是强对偶的，也就是MCP(1)与(5)强对偶。

命题1Λ*-A是奇异的。

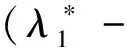
算法1 (Modified Dual Method，MDM)

第二步 计算Λ*-A的最小特征值对应的特征向量

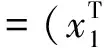
第三步 如果‖xj‖2≥1-ε0(这里ε0为某一给定的小正数)，j=1,2…,m，则x*为MCP的全局解，停机，否则执行下一步；

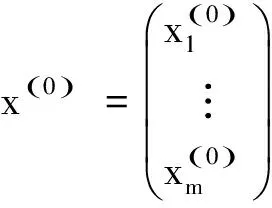
对于上述算法有以下几点说明：

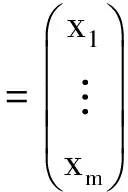
其中vi是Aii对应最大特征值的单位特征向量。

其次，正如引言所指出的，如果m=2或者m≥3且A为正矩阵，那么，Hanafi和Ten Berge[8,Result 5]表明：(3)与(5)是强对偶的，此时算法1中的Step(4)理论上是不必要的，即x*是MCP(1)的全局解。

第三，对于m≥3且A为一般的正定矩阵时，算法1的本质是：若(3)与(5)是强对偶的，则Step(3)结束后即可获得MCP(1)的全局解；若(3)与(5)不是强对偶的，即(6)没有解x*∈Σm，此时对偶方法为对称G-S或AVM迭代法提供一种初始迭代策略。

(7)

令

(8)

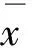
(9)

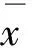
已知，对对称G-S及AVM方法而言目前已有的理论无法保证获得MCP(1)的全局最大点，已有的数值实验表明[16-17]，恰当地选择初始迭代点不但可以提高Horst方法、G-S方法及P-SOR方法的收敛速度，而且可以提高获取(1)的最优解的可能性。

2 数值实验

本文的数值实验是在Matlab7.6.0环境下完的，而且所用的矩阵A按如下2种方式形成：

首先，对上述2种方式形成的矩阵A做了充分的实验，分别统计了MCP与其Lagrange对偶问题强对偶的概率。结果表明：矩阵A=DBTBD对应的MCP与其Lagrange对偶问题都是强对偶的,并且强对偶性与m和整数集p的取值无关(统计应用中常出现这类矩阵)；而对于方式二形成的矩阵并非都是强对偶的(见表1)，只有当m=2时全是强对偶的，而且随着m的增大，强对偶的概率减小；并且随着m和n的增大，平均花费时间增加，即，算法收敛速度变慢。

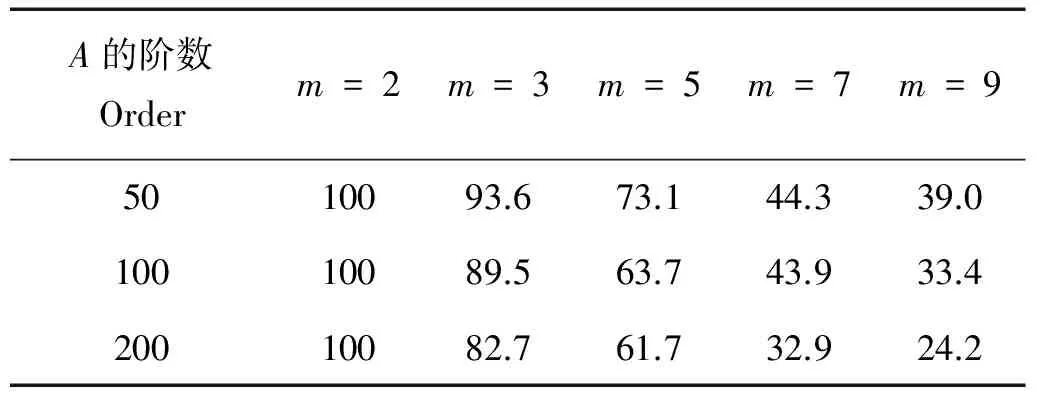
表1 强对偶的概率

由于MCP的Lagrange对偶问题是半定规划，并且已有较好的求解软件，因此，对于方式一中形成的矩阵A，可以通过求解其对偶问题来获得MCP的全局解；而对于方式二中对应的非强对偶的情形，用改进的对偶方法(MDM)进行求解(见表2)，并统计此时获得全局解的可能性。

表2 获得全局解的可能性

表2中的结果表明，改进的对偶方法对于获得MCP的全局解有改进，但对于困难问题仍不保证得全局解。

其次，为了更好的了解对偶方法对获得全局解的改进，给出几个已知全局解的例子进行数值实验。

例1 取自[8]

m=3,p={2,2,2},ρ(x*)=378.9624。

例2 取自Chu和Watterson[3]

m=2,p={2,3},ρ(x*)=14.7302。

例3 取自Xu[17]

m=3,p={3,3,4},ρ(x*)=103.6819。

例4 取自Zhang,Liao and Sun[18]

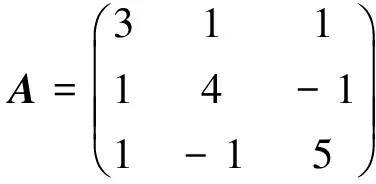
m=3,p={1,1,1},ρ(x*)=14.000。

对上述给定的例子，利用Sedumi软件求解其MCP的对偶问题，比较MCP与其对偶问题的最优值(Table3)。

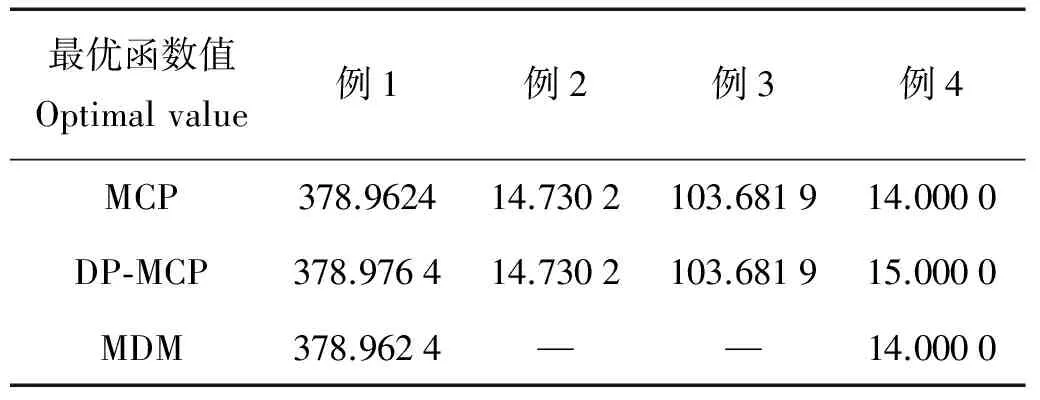
表3 最优值的比较

根据上述结果，可以清楚地看到，例2和3对应的MCP与其对偶问题是强对偶的，那么我们可以通过求解其对偶问题得到MCP的全局最优解；而例1和4的MCP与其对偶问题是弱对偶的，并且此时利用修改的对偶方法(MDM)可获得MCP的全局最优解和全局最优值。

表4 对偶差

若MCP与其对偶问题是强对偶的，则此时μ为零，即对偶问题的解是MCP的解；而当非强对偶时(表4)，μ的值不大，那么在一定的精度下，可以把对偶问题的解作为MCP的近似解；而此时若用改进的对偶方法求解MCP，则可以有效地获得MCP的全局解。

[1] Hotelling H. The most predictable criterion [J]. J Educ Pyschol, 1935, 26: 139-142.

[2] Hotelling H. Relations between two sets of variates [J]. Biometrika,1936, 28: 321-377.

[3] Chu M T, Watterson J L. On a multivariate eigenvalue problem, Part I: Algebraic theory and a power method [J]. SIAM J Sci Comput, 1993(14): 1089-1106.

[4] Horst P. Relations among m sets of measures [J]. Psychometrika,1961, 26: 129-149.

[5] Hu D K. The convergence property of a algorithm about generalized eigenvalue and eigenvector of positive definite matrix [C]. Beijing: China-Japan Symposium on Statistics, 1984.

[6] 孙继广. 多参数特征值问题的一种算法[J]. 计算数学, 1986, 8(2): 137-149.

[7] 秦晓伟. 关于解极大相关问题P-SOR算法的收敛性 [J]. 计算数学， 2011, 33: 345-356.

[8] Hanafi M, Ten Berge J M F. Global optimality of the successive Maxbet algorithm [J]. Psychometrika, 2003(68): 97-103.

[9] Zhang L H, Liao L Z. An alternating variable method for the maximal correlation problem [J]. J Global Optim, DOI: 10. 1007/s 10898-011-9758-2.

[10] Grzegórski S M. On the convergence of the method of alternating projections for multivariate symmetric eigenvalue problem [C]. Chania: Conference in Numerical Analysis, 2010: 15-18.

[11] Liu X G, Wang K. A multigrid method for the maximal correlation problem,Numerical Algebra [J]. Control and Optimization, 2012, 2(4): 785-796.

[12] Nocedal J, Wright S J. Numerical Optimization [M]. New York: Springer, 1999.

[13] Boyd S, Vandenberghe L. Convex Optimization [M]. Cambridge: Cambridge University Press, 2004.

[14] JOS F. STURM,(using sedumi 1.02)A Matlab toolbox for optimization over symmetric cones [EB/OL]. Available online: http: //fewcal.kub. nl/～sturm.

[15] Steven J. Benson, DSDP5 user guide-Software for semidefinite programming [EB/OL]. http: //www.mcs. anl.gov/～benson

[16] Zhang L H, Chu M T. Computing absolute maximum correlation [J]. IMA J Numer Anal, 2011, DOI: 10.1093/imanum/drq029.

[17] 徐莲花. 关于多元特征值问题的数值方法 [D]. 青岛： 中国海洋大学数学科学学院, 2008.

[18] Zhang L H, Liao L Z, Sun L M. Towards the global solution of the maximal correlation problem [J]. J Global Optim, 2011(49): 91-107.

AMS Subject Classification: 62H20

责任编辑 陈呈超

A Dual Method for the Maximal Correlation Problem

LI Mei-Ran， LIU Xin-Guo
(School of Mathematical Sciences, Ocean University of China, Qingdao 266100, China)

The maximal correlation problem aiming at assessing the relationship between sets of variables plays a very important role in many areas of statistical application. Currently, several algorithms for the global maximizer of the MCP have been proposed, but they can not guarantee convergence to a global solution. In the present paper,by solving the dual problem of the MCP, a modified Lagrange dual method is proposed. Numerical experiments demonstrate the new algorithm can increase the probability of finding a global maximizer.

maximal correlation problem； multivariate eigenvalue problem； lagrange dual； strong dual； global maximizer； convergence

国家自然科学基金项目(11371333)资助

2013-10-12；

2014-05-10

李美然(1988-)，女，硕士生。E-mail：limeiran5211314@126.com

O212.4

A

1672-5174(2015)08-128-05

10.16441/j.cnki.hdxb.20130323