爆破动力荷载下边坡稳定性的时程分析

陈鹏辉 楼晓明,2 周文海(.福州大学紫金矿业学院，福建 福州 3506；2.福州大学爆炸技术研究所，福建 福州 3506)

爆破动力荷载下边坡稳定性的时程分析

陈鹏辉1楼晓明1,2周文海1(1.福州大学紫金矿业学院，福建 福州 350116；2.福州大学爆炸技术研究所，福建 福州 350116)

针对露天矿开采过程中，爆破开挖作业对最终边坡稳定的影响问题，采用动力有限元法分析爆破过程中边坡的稳定性随时间变化情况。首先建立矿山边坡的二维有限元模型，利用有限元强度折减法求解，得到边坡的最危险滑动面及折减安全系数；再根据得到的最危险滑动面，重新建立边坡和炸药的三维实体模型，布置爆破孔网参数并设置各个炮孔的起爆时间，通过LS-DYNA大型动力有限元程序，求解边坡在炸药爆炸后30 s时间内的动力响应过程。结合极限平衡法和动力有限元法计算结果，计算边坡在同时起爆方式下每一时刻的安全系数。提出应根据边坡时程安全系数及边坡滑面单元是否同时发生整体破坏等条件综合评价边坡稳定性。数值模拟结果能够动态显示爆破过程中边坡的应力、应变状态，计算结果与极限平衡法计算结果接近，可以为露天矿爆破设计提供参考。

动力稳定 安全系数 时程分析 LS-DYNA 数值模拟

爆破荷载下岩质边坡的动力响应及控制是矿山开发和工程建设中面临的一个亟待解决的课题。边坡稳定是露天矿安全生产的前提，随着露天矿不断进入深凹开采，爆破地震效应对边坡稳定的影响问题日益突出。炸药爆炸过程是一个短暂且复杂的过程，一般认为，爆破动力荷载对边坡稳定性的影响主要是因为反复的爆破振动引起边坡稳定性减弱，岩体结构抗剪强度指标降低而产生的衰减失稳以及爆破振动自身产生的地震惯性力导致坡体整体的下滑力增大，最终引起整个坡体的惯性失稳[1]。

衰减失稳通常采用变形破坏分析法和流动破坏分析法；而惯性失稳主要的分析方法有Newmark滑块分析法、拟静力法、Makidisi Seed法以及有限元法等。现阶段岩质边坡的动力稳定数值模拟中，爆破动力荷载的加载方式大多采用以下几种方法：采用实测或人工合成的爆破振动速度、加速度时程曲线等转换为爆破动力荷载[2-5]，或者采用理论计算的等效爆轰压力施加在孔壁或炮孔连心线所在的平面上等方法进行动力响应时程分析[6-7]。

1 有限元法+极限平衡法

在传统的边坡稳定性分析中，极限平衡法和有限元法一般都是分开分析的。极限平衡法因其原理简单、计算简便，在工程上具有广泛的应用，积累了丰富的实践经验。而有限元法不需要预先假设滑动面，同时考虑了岩体应力-应变关系，能够真实反映岩体的实际情况，更适合分析大型、复杂的地质边坡。利用有限元法得到边坡的最危险滑面，通过有限元软件对滑面进行单元划分。将动力分析后得到的滑动面单元应力结果σxi、σyi、σxyi，结合极限平衡法计算边坡的安全系数[8-9]，如图1及公式(1)。

图1 有限元法+极限平衡法

(1)

式中，σi为作用在弧段上的法向应力(有限元计算以拉为正，压为负)；τi为作用在弧段上的剪应力；σxi，σyi，σxyi为有限元计算得到的应力;θi为弧段Δli与x轴的夹角;τfi为抗剪强度;li为弧段长度。

2 工程实例

在矿山正常生产作业过程中，爆破作业从设计到施工是一个系统工程。在利用有限元软件进行建模分析时，受到模型材料参数、地形地质条件等因素的制约。特别是在建立三维模型的时候，划分单元数量会急剧增加，对计算机的硬件配置提出更高的要求。以青海威斯特铜矿为基础，建立一个台阶的计算模型。岩石密度2.5g/cm3，弹性模量22.5GPa，泊松比0.22，黏聚力0.22MPa，内摩擦角27.4°。首先采用有限元强度折减法[10-13]计算二维平面应变状态下边坡的最危险滑动面，再按照现场爆破参数建立三维实体模型及炸药模型，运用LS-DYNA程序求解爆破过程中边坡滑面上单元的应力应变状态，分析边坡在爆破动力作用下稳定性随时间变化情况。

2.1 数值建模

模型采用cm-g-us单位制，台阶高度24m(并段后)，坡面角70°，台阶尺寸如图2。设计孔网参数为孔距6m，排距5m，孔径150mm，孔深14m，装药长度9m，填塞长度5m，采用耦合装药方式，单孔药量为192kg，共布置3排10个炮孔。台阶模型尺寸根据郑颖人等[10]的研究经验，坡脚至左边界延伸坡高的1.5倍，坡顶线至右边界延伸坡高的至少2.5倍，上下边界距离至少为2倍的坡高建模。以台阶横向为X轴，竖向为Y轴，纵向为Z轴，三维状态下Z轴延伸50 m，即台阶爆破区域长50 m，宽36 m。台阶岩体采用塑性随动强化模型，炸药采用2#岩石乳化炸药，炸药密度0.95 g/cm3，爆速3 600 m/s，填塞材料和台阶岩体材料一致。

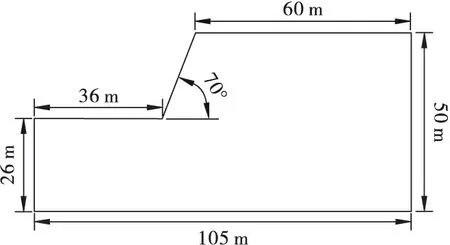
图2 台阶平面模型

在爆炸场的数值模拟中，采用美国劳伦斯·利弗摩尔实验室的Lee等提出JWL状态方程[14]：

(2)

式中,p为状态方程决定的压力；A，B，R1，R2，w为描述JWL方程独立的5个物理常数;V是相对体积；E0为初始内能。炸药及状态方程具体取值如表1所示。

表1 炸药及其状态方程参数Table 1 Explosive and its parameters in state equation

2.2 网格划分及加载约束

如图3，模型网格二维状态下严格按照四边形，三维状态六面体进行网格划分。二维分析模型总共划分4 521个单元，三维模型总共划分170 958个单元。二维模型底部和左右边界施加位移约束，边坡面积坡顶为自由边界；三维模型除台阶面和台阶坡面为自由边界以外，其余边界均施为透射边界(无反射边界)条件。二维模型施加重力荷载，三维模型利用动力松弛加载预应力，在动力求解过程中保持重力加载。

图3 台阶二维和三维网格划分

3 结果分析

3.1 静力求解结果

二维静力计算时，采用二分法不断地折减内摩擦系数和黏聚力，根据台阶坡面广义塑性应变或者等效塑性应变从坡脚到坡顶贯通、计算不收敛、边坡单元或节点位移发生突变等边坡失稳判据[11]判断边坡是否失稳。得到在折减系数取2.750时，边坡塑性区域已经贯通，但边坡并没有破坏，处于临界破坏状态。当折减系数继续增大时，边坡塑性应变区域贯通(见图4)，计算机计算不收敛，节点位移发生突变，同时发生边坡失稳，发生破坏。

图4 塑性区域贯通

利用有限元强度折减法得到静力状态下边坡的最危险滑面(见图5)，结合传统的极限平衡法，计算边坡静态下的安全系数，具体结果见表2。传统的极限平衡法计算结果和有限元计算结果比较接近，相对误差在3%左右。

图5 边坡最危险滑面

表2 极限平衡法和静态有限元法计算结果Table 2 The results of limit equilibrium method and FEM

3.2 动力有限元求解结果

为便于分析，本次模拟第1排3个炮孔同时起爆，同段起爆药量为576 kg，计算时间分别为1 s、5 s、30 s 3种时长。选取边坡坡脚(H2)、坡面(H5738)、坡顶(H5381)及上台阶面单元(H28944)进行分析，各点距离爆心的水平距离分别为10.80、15.53、19.80、52.58 m，如图6所示。

图6 单元位置

(1)边坡应力响应分析。在炸药爆炸过程中，对炮孔中间位置每隔10 ms进行应力云图切片观察。炸药起爆后，孔壁压力迅速上升，炮孔壁上单元的最大应力达49 MPa，达到峰值后快速衰减，在60 ms左右下降到0.2 MPa。而边坡表面的测点有效应力明显小于炮孔周围的单元，坡脚单元有效应力大于其他测点，其最大值达1 MPa。另外，边坡测点的最大主应力，最小主应力以及最大剪应力都在坡脚附近单元出现应力集中现象，但出现的时间都很短暂，在爆炸结束后，基本趋于稳定值。

(2)边坡位移响应分析。由计算结果得知，坡顶位置出现较大的位移波动，波动范围为-0.35～0.25 cm，坡脚及坡面单元基本集中在-0.1～0.1 cm。在测点的Y轴、Z轴位移监测中，最大值均出现在坡顶及其附近单元。边坡内滑面单元X轴位移最大值为5.4 s时的0.019 8 cm，最小值为0.3 s时的-0.029 8 cm；Y轴位移最大值为6.3 s时的0.031 4 cm，最小值为0.6 s时的-0.079 cm；Z轴位移最大值为0.3 s时的0.000 916 cm，最小值为0.9 s时的-0.002 14 cm。虽然最值发生的时间不一致，但是最大值均发生在靠近坡脚的地方。

(3)边坡速度响应分析。由于矿山边坡是一个临时边坡，并且边坡的状态随时可能发生改变，目前尚无一个能够判断边坡稳定性的安全振速统一标准。从图7时程曲线中可知，坡顶单元的振动速度明显高于其他部位单元，出现速度放大效应。坡顶振动速度最大值达到17 cm/s，坡脚振动速度最大值为8 cm/s。测点合速度中，坡顶速度依然大于其他部位，最大值为0.9 s时的18.9 cm/s。

图7 测点Y轴振动速度

3.3 安全系数时程分析

根据程序计算结果，在后处理软件LS-PREPOST中提取出滑面单元在爆炸过程中的X、Y、XY轴应力，利用式(1)进行时程安全系数计算(见图8)。计算结果如表3所示。

图8 边坡三维有限元计算模型

表3 动力有限元计算结果Table 3 The results of dynamic FEM

在爆破动力作用下，边坡内部应力状态时刻在发生变化，其时程安全系数在静态安全系数一定范围内上下波动，随着时间的增加，时程安全系数又趋于稳定。由于3种时长的计算结果在提取时间的间隔上有差异，结果也存在一定差异。从侧面反映了炸药爆炸动力荷载对边坡岩体的瞬时作用特性。爆炸过程中，时程安全系数在个别时刻由于受到爆炸冲击波的作用，个别单元应力发生突变，导致整体安全系数在瞬间会突然增大或减小，最大值达到12.434，是初始值的4.5倍，最小值为0.907，比初始值降低66.68%，但很快均返回到正常范围。刘汉龙等[2]采用最小平均安全系数，即静力下的安全系数Fs0与最小动力安全系数Fs min差值的0.65倍作为安全系数的平均振幅来反应安全系数因振动作用而偏离的幅度，计算得最小平均安全系数

虽然滑面单元在个别时刻应力发生突变，但滑面单元的最大剪应力并没有达到破坏值。模拟结果显示，边坡的有效塑性应变只发生在坡脚的部分单元，边坡的坡面及内部并没有发生失效破坏，边坡整体还是稳定的。当边坡的初始安全系数比较低时，随着这种单元应力突变次数的增加，边坡内部就很有可能因损伤累积效应发生失稳破坏。单元应力状态的突变是边坡失稳的潜在危险因素。因此，采用时程安全系数中的最小值或者最小平均安全系数作为边坡稳定性的判据是不够准确的。应该同时结合边坡滑面单元的塑性应变及位移情况，最大剪应力是否达到破坏等条件综合评价边坡的稳定性。

4 总 结

(1)利用动力有限元法，能直观显示在爆破动力荷载下边坡安全系数随时间的变化情况。同时，在计算精度上与传统极限平衡法相当接近，为边坡稳定性设计及爆破参数优化提供参考。

(2)通过LS-DYNA程序可以直接模拟三维状态下高能炸药爆炸的整个动力作用过程。根据工程实际，建立爆破实体模型，设置任意起爆时间和起爆顺序，简化了爆破动力的加载方式和加载时间。同时，结合有限元强度折减法分析边坡在爆破动力下的时程响应规律，简化了最危险滑动面搜索的工作量。

图9 极限平衡法与有限元法计算结果比较(T=30 s)

(3)为便于模拟分析，本研究没有考虑节理裂隙、孔隙水等因素对岩质边坡的影响。另外，由于炸药爆炸过程时间及其短暂，远小于现实的延期时间和爆破后冲击波对边坡的作用和反应时间，如果要完整计算长时间下边坡的动力响应，可以根据实际情况在不影响实验结果的前提下对模型参数进一步优化，以减少计算机计算时间和对计算机内存空间的占用。

[1] 刘立平,雷尊宇,周富春.地震边坡稳定分析方法综述[J].重庆交通学院学报,2001,20(3):83-88. Liu Liping,Lei Zunyu,Zhou Fuchun.The evaluation of seismic slope stability analysis methods[J].Journal of Chongqing Jiaotong University,2001,20(3):83-88.

[2] 郑颖人,叶海林,黄润秋,等.边坡地震稳定性分析探讨[J].地震工程与工程振动,2010(2):173-180. Zheng Yingren,Ye Hailin,Huang Runqiu,et al.Study on the seismic stability analysis of a slope[J].Journal of Earthquake Engineering and Engineering Vibration,2010(2):173-180.

[3] 刘汉龙,费 康,高玉峰.边坡地震稳定性时程分析方法[J].岩土力学,2003(4):553-556. Liu Hanlong,Fei Kang,Gao Yufeng.Time history analysis method of slope seismic stability [J].Rock and Soil Mechanics,2003(4):553-556.

[4] 许名标,彭德红.边坡爆破振动测试及响应规律ANSYS时程分析[J].岩石力学与工程学报,2012(S1):2629-2635. Xu Mingbiao,Peng Dehong.Blasting vibration tests and analysis time-history analyses of slope responses[J].Chinese Journal of Rock Mechanics and Engineering,2012(S1):2629-2635.

[5] 陈 明,卢文波,舒大强,等.爆破振动作用下边坡极限平衡分析的等效加速度计算方法[J].岩石力学与工程学报,2009(4):784-790.

Chen Ming,Lu Wenbo,Shu Daqiang,et al.Calculation method of equivalent acceleration for limit equilibrium analysis of slope under blasting vibration[J].Chinese Journal of Rock Mechanics and Engineering,2009(4)：784-790.

[6] 赵婉婷,卢文波,杨建华,等.深孔台阶爆破振动模拟中的等效荷载施加边界比较[J].爆破,2012(2):10-14. Zhao Wanting,Lu Wenbo,Yang Jianhua,et al.Comparison of equivalent load in boundaries in deep-hole bench blasting vibration simulation[J].Blasting,2012(2):10-14.

[7] 许红涛,卢文波,周创兵,等.基于时程分析的岩质高边坡开挖爆破动力稳定性计算方法[J].岩石力学与工程学报,2006(11):2213-2219. Xu Hongtao,Lu Wenbo,Zhou Chuangbing,et al.Time history analysis method for evaluating dynamic stability of high rock slope under excavation blasting[J].Chinese Journal of Rock Mechanics and Engineering,2006(11)：2213-2219.

[8] 陈祖煜.土质边披稳定分析——原理·方法·程序[M].北京:中国水利水电出版社,2003:255-256. Chen Zuyu.Soil Slope Stability Analysis：Theory Methods and Programs[M].Beijing:China Water Power Press,2003:255-256.

[9] 王成华.土力学[M].武汉:华中科技大学出版社,2010:346-348. Wang Chenghua.Soil Mechanics[M].Wuhan:Huazhong University of Science & Technology Press,2010:346-348.

[10] 郑颖人,赵尚毅.有限元强度折减法在土坡与岩坡中的应用[J].岩石力学与工程学报,2004,19:3381-3388. Zheng Yingren,Zhao Shangyi.Application of strength reduction fem in soil and rock slope[J].Chinese Journal of Rock Mechanics and Engineering,2004,19:3381-3388.

[11] 赵尚毅,郑颖人,张玉芳.有限元强度折减法中边坡失稳的判据探讨[J].岩土力学,2005(2)：332-336. Zhao Shangyi,Zheng Yingren,Zhang Yufang.Study on slope failure criterion in strength reduction finite element method[J].Rock and Soil Mechanics,2005(2):332-336.

[12] 马建勋,赖志生,蔡庆娥,等.基于强度折减法的边坡稳定性三维有限元分析[J].岩石力学与工程学报,2004,16:2690-2693. Ma Jianxun,Lai Zhisheng,Cai Qing′e,et al.3D FEM analysis of slope stability based on strength reduction method[J].Chinese Journal of Rock Mechanics and Engineering,2004,16:2690-2693.

[13] 郑颖人,赵尚毅.岩土工程极限分析有限元法及其应用[J].土木工程学报,2005(1):91-98. Zheng Yingren,Zhao Shangyi.Limit state finite element method for geotechnical engineering analysis and its applications[J].China Civil Engineering Journal,2005(1):91-98

[14] Livemore Software Technology Corporation.LS-DYNA Version 971 Keyword User′s Manual[M].California:Livemore Software Technology Corporation,2007.

(责任编辑 徐志宏)

Time History Analysis of Slope Stability under the Blasting Loading

Chen Penghui1Lou Xiaoming1,2Zhou Wenhai1
(1.CollegeofZijinMining,FuzhouUniversity,Fuzhou350116,China;2.ResearchInstituteofExplosionTechnology,FuzhouUniversity,Fuzhou350116,China)

For the significant impact of blasting on slope stability during open-pit mining process,the dynamic finite element method is used to analyze the variation of slope stability with the time in blasting.Firstly,the finite element model of mine slope is established,then the finite element strength reduction method is adopted to get the most dangerous sliding surface and safety coefficient of the slope.After that,based on the most dangerous sliding surface obtained,a three-dimensional entity model of slope and explosives was created,the blasting parameters are arranged and the initiation time for each hole is set up.Next,this model is calculated after the initiation.The dynamic response process after slope explosive for 30 s is solved by LS-DYNA large dynamic finite element program.Combining with the limit equilibrium method and dynamic finite element method,the safety factors of slope at every moment under unified detonation are calculated.Slope stability should be comprehensively evaluated by the time-history safety coefficient and whether the elements of the sliding surface are destroyed at the same time.The simulation results can dynamically display the security status of slope blasting process,and the result is very close to that by the limit equilibrium method.This research could make a reference for the blasting design.

Dynamic stability,Safety coefficient,Time history analysis,LS-DYNA,Numerical simulation

2014-10-29

福建省自然科学基金项目(编号：2001J01310)。

陈鹏辉(1990—)，男，硕士研究生。通讯作者 楼晓明(1972—)，男，博士，副教授。

TD235

A

1001-1250(2015)-11-029-05