带援助和伪障碍的Geom/Geom/1休假排队模型
孟 俊
(喀什大学 数学与统计学院,新疆 喀什 844006)
带援助和伪障碍的Geom/Geom/1休假排队模型
孟 俊
(喀什大学 数学与统计学院,新疆 喀什 844006)
在离散时间Geom/Geom/1工作休假排队系统中,同时考虑外来支援与伪障碍两个因素,这个组合丰富了原有的排队论模型.外来援助帮助系统减少顾客,一对一抵销队尾顾客.若系统突然停止工作,则称系统有障碍出现,障碍分为真障碍和伪障碍两类.本文应用拟生灭链和矩阵几何解的方法,得到了模型各状态的稳态分布,队长和等待时间在稳态条件下的随机分解.
援助; 伪障碍;工作休假;矩阵几何解;条件随机分解
0 引言
20世纪中后期,在信息传输系统,电话交换网络和物流传输系统的迅速发展的带动下,休假排队论的研究已经日渐成熟.Neuts[1]等开创的矩阵几何解法成为排队论的核心内容.近些年来,半休假策略被Servi和Finn[2]引入到了排队论中,半休假也称为工作休假此后有关工作休假策略的排队论就大量出现,如文献[3-6].关于Geom/Geom/1排队论模型是源于20世纪提出了到达间隔和服务时间为正整数值随机变量的离散时间排队.后来朱翼隽[7]等将负顾客引入Geom/Geom/1排队论模型中,随之有关负顾客的离散时间工作休假模型也陆续出现,如文献[8-11].但是考虑到一个完善的系统会有备用帮助和取消信号的行为,我们统称这些为外来援助.并且系统中必然存在诱使服务中止的因素存在,我们将这种因素称为伪障碍.因此,本文在前面文献的基础之上,补充研究了带外来援助和伪故障的单服务台Geom/Geom/1工作休假排队模型的平衡条件,各状态的稳态分布,稳态下队长和等待时间的条件随机分解结构.
1 模型描述和记号
(1)顾客和外来援助抵达间隔相互独立,假设顾客和援助能够同时抵达,抵达概率分别为p和q,分别服从G(p),G(q)的分布,其中0 (2)假设ub和uv是忙期和假期中顾客在一个时间间隔内被效劳完毕的概率,在忙期和假期中系统效劳一个顾客的时间分别为Sb和Sv,且Sb▯G(ub),Sv▯G(uv): 其中0 (3)假设休假的起始与结束只出现在n处,n=0,1,…,假设该模型的工作休假策略为:当队长为0时,系统进入一个时长V为的工作休假,且V▯G(θ): 队长为0时,系统启动一个时长为V的工作休假的方式和启动忙期的方式为: 在工作或者休假期间,服务台进入另一次独立同分布的工作休假的情况有:a.效劳完一个顾客后,若队长为0;b.若系统内只有外来援助,则外来援助离开;工作休假期间效劳速率为uν,按到达次序接受效劳.若工作休假结束时系统队长不为0,则效劳速率由uν切换到ub,启动一个正规忙期. (4)伪故障只发生忙期,若发生伪故障,则系统重新进入休假状态,等休假结束进入忙期;若发生故障,则立即进行修理.修理时间R▯G(γ),即: 修复完善后立即启动工作,为效劳完毕的顾客重新效劳. (5)设Ln表示在时刻n处的队长长度,即顾客数,且假设: (6)到达间隔,Sb={忙期服务时间},Sν={工作休假期服务时间},V={休假时间}相互独立,按到达顺序效劳. 各个状态的平稳分布以及稳态条件下队长的随机分解: 将带负顾客和伪故障的离散时间休假排队系统的状态参照系统中的顾客数和系统得状态排列,该模型的转移概率矩阵为: (1) 其中 易知研究该链能够采取Neuts[1]等创造的矩阵几何解方法.因为通过观察(1)的结构发现{(Ln,Jn),n≥0}是不可约,非周期的拟生灭链,可以将(1)看为GI/M/1型结构矩阵的变形. 该模型的稳态分布为: 其中 则稳态队长的随机分解为: 其中 定理1 若α<1且θ>0,稳态条件下等待时间有随机分解: 其中 证明:顾客抵达不需等待的概率是: 如果抵达发生在工作休假期内,队长为k,则会产生下列情况之一: (1) 如果抵达发生在时刻n,时刻n有效劳完毕一个顾客,另外k-1个顾客进入正规忙期,按速率ub效劳; (2) 如果在时刻n没有效劳完毕一个顾客,并且Sν≤V,即剩余休假时间大于或等于按速率uν效劳完毕一个顾客的剩余时间,则按速率uν效劳一个顾客,接下来按速率uν效劳第二个顾客,并再次看工作休假是否中止,如此循环下去,工作休假内的效劳完成后将中止休假系统启动正规忙期: 下面求此差分方程,求出Wk0:设ω<1,记 于是可得 于是 所以 因为W00(z)=P{W=0},所以 因此 其中 在离散时间Geom/Geom/1工作休假排队系统中,同时考虑外来援助与伪障碍两个因素,这个组合丰富了原有的排队论模型,更贴近实际模型的应用,成功模拟了实际的计算机系统,通信工程中如果出现信号取消或者信号中断问题时的稳态条件下队长和等待时间的随机分解.此模型的研究方法同样适用于其它离散时间排队模型,例如Geom/G/1,Geom/Geom/N等.总之,有关离散时间排队论的研究还可以进行更实际更深层次的探索. [1] Neuts M. Matrix-geometric Solution Stochastic Models[M].Baltimore:Johns Hokpins University Press,1981. [2] Servi L D,Finn S G.M /M /1 Queue with Working Vacations( M/M/1/WV)[J].Perform Evaluation,2002,50: 41-52. [3] 朱翼隽,石秀闯. M/G/1工作休假和休假中止排队[J].运筹与管理,2008,17( 4) : 67-71. [4] 汪文飞,李俊平.带单重指数工作休假和休假中断的 GI/M/1的排队系统[ J].数学理论用,2009,29( 3):94 -97. [5] Li,TianN.Analysis of the Discrete Time Geo/Geo/1 Queue with Single Working Vacation[J].Quality Technology and Quantitative Management,2008,5(1):77-89. [6] Li Jihong,Tian Naishuo,Ma Zhanyou. Performance Analysis of GI /M /1 Queue with Working Vacations and Vacation Interruption[ J].Applied Mathematical Modeling,2008,32(12):2715-2730. [7] Zhu Yijun,Zhu Shang,The Geo/Geo/1 Queue with woking vacation andnegative customers and vacation terruption. Journal of HeNan Normal University.Vol.40No.2Mar.2012. [8] 田乃硕,徐秀丽,马占友.离散时间排队论[M].北京:科学出版社,2008. [9] Zhu Y J,Song N,Zhou Z H. Discrete time Geo /Geo /1 queuewith negative customers and multiple working vacations[J].Journal of Jiangsu University: Natural Science Edition,2010,31(4):488-491. [10] 唐学德,朱翼隽,冯艳刚.具有两种服务的负顾客 M~ζ/(G_1/G_2)/1排队系统[J].江西师范大学学报(自然科学版),2007,31(5):500-503. [11] 朱桂仙,徐德举. N策略多重工作休假 Geo /Geo/1离散时间排队[J] . 首都师范大学学报(自然科学版),2009,30(4):1-15. Geom/Geom/1 working vacation queue with assistance and false malfunction MENG Jun (SchoolofMathematicsandStatistics,KashiUniversity,KashiXinjiang844006,China) Takeassistance and false malfunction into discrete time queue with vacation interruptionstrategy.Thiscombinationenrich known queuing model.The assistance offset the positive customers who are being served from the head of the queue one by one.If thesystem suddenly stopped working,thissystem failure.There are true and false failure.This paperuse quasi-birth-and-death process and matrix-geometric solution method, thesteady-state distributions for queue length and the probability generating function are given.Then the stochastic decomposition structure of queue length and sojourn time in the stationary state is gained and obtained the distributionsfor additional queue length and additional waiting timeby this paper. Assistance; False malfunction; Vacation interruption; Matrix-geometric solutionstocha; Stic decomposition 2015-08-15 孟 俊(1987-),女,河南开封人,硕士,助教,研究方向:概率论. 1001-9383(2015)03-0012-05 O211 A


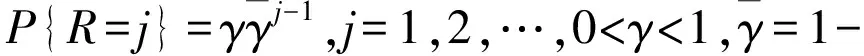
2 状态转移分析

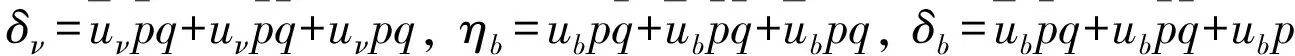
3 稳态条件下等待时间的随机分解
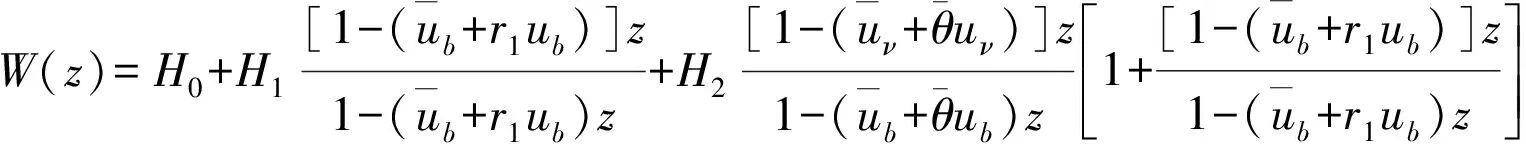


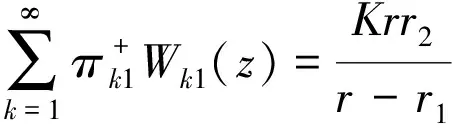


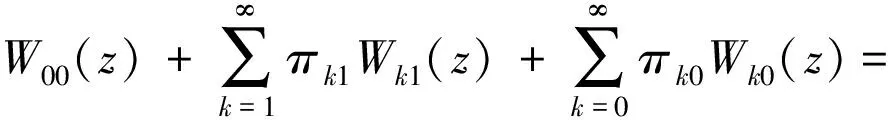

4 结语

