基于频谱能量的材料晶粒尺寸表征方法

黎 敏，周 通，王善超，肖会芳，徐金梧

(1 北京科技大学 机械工程学院，北京 100083；2 北京科技大学国家板带生产先进装备工程技术研究中心，北京 100083)



基于频谱能量的材料晶粒尺寸表征方法

黎 敏1，周 通1，王善超1，肖会芳2，徐金梧1

(1 北京科技大学 机械工程学院，北京 100083；2 北京科技大学国家板带生产先进装备工程技术研究中心，北京 100083)

研究了利用超声频谱能量对材料晶粒尺寸进行表征的方法。通过不同的热处理方式获得了不同晶粒尺寸的奥氏体不锈钢材料，再分别利用衰减系数法、声速法和频谱能量法对材料的晶粒尺寸进行表征。结果表明：频谱能量法得到的衰减系数与平均晶粒尺寸呈非线性关系，晶粒尺寸的预测误差在4%～15%以内，优于传统的分析方法，证明了新方法的有效性。

超声检测；晶粒尺寸；衰减系数；声速；频谱能量

晶粒尺寸是影响材料力学性能(如疲劳、蠕变和屈服强度)的重要参数。对金属材料的晶粒尺寸检测常采用金相法，但该方法需要对材料表面进行打磨，试件的制备过程复杂、周期长，检测结果只能反映材料表层的晶粒大小，无法实现在线检测。超声检测技术是一种无损检测方法，且制样过程简单、检测范围大、具有一定的穿透深度，可以获得材料内部的晶粒结构特征，因此该技术逐渐被应用到材料内部结构的检测中[1-3]。采用的方法主要有超声衰减法、超声声速法和频谱分析法等。在衰减法方面，早期的工作局限于机理研究[4，5]，发现晶粒散射大小主要取决于平均晶粒尺寸，且与晶粒的分布和取向有关，尤其在瑞利散射区内，晶粒散射是超声波衰减的主要因素。随后，进行晶粒尺寸的定量评价工作[6，7]，对碳钢、合金钢等材料的晶粒度进行表征。发现在确定的发射频率下，材料的晶粒平均尺寸增大，超声波的衰减系数也随之增大，与金相法的测量结果相比，衰减法对材料晶粒度表征的误差往往大于20%，最大偏差在35%左右[8]。随着检测设备精度的提高，基于超声衰减法晶粒度表征的准确性有所改善。在声速法方面，发现晶粒尺寸和取向与材料的密度、弹性模量、泊松比有关，而上述这些材料属性又与超声的声速有关。因此，晶粒尺寸和取向间接地影响声速的大小，意味着当材料的平均晶粒尺寸发生变化时，材料中的声速也会相应改变。利用声速法来表征材料晶粒度的误差一般在20%左右，但声速法受材料自身属性的影响极大[6,9,10]。当检测材料不同时，实验结果就发生较大波动，如不锈钢材料的晶粒尺寸增大时，纵波声速减小；而陶瓷-金属复合材料的晶粒尺寸增大时，纵波声速却是增大的。因此，利用声速法来评估材料的晶粒度时很难发现一般规律，通常是与衰减法联合使用，互相验证。随着信号处理技术的发展，将基于傅里叶变换的频谱分析技术引入到了超声检测领域。由于材料内部相邻晶粒间存在声阻抗差，使得超声波的高频部分有明显的衰减，而低频部分的衰减相对较少，因此可以通过对超声回波的频谱分析来研究材料的平均晶粒尺寸的变化[11]。张洪达等[12]研究发现，超声底面回波的峰值频率随着Cr-Mo钢的晶粒尺寸增加而减小。Badidi等[13]发现，采用峰值频率来表征晶粒尺寸的方法对轧制材料更适用。李萍等[14]对304奥氏体不锈钢固溶产物的晶粒尺寸进行了表征，研究表明谱峰高度对晶粒尺寸变化敏感。目前，运用频谱分析法来实现材料的晶粒尺寸评价还处于起步阶段，主要存在如下问题：峰值频率、谱峰高度等频谱特征参数反映的是超声回波信号的基频成分及其对应的能量大小，不能完全代表超声回波的全部特征。此外，单独地只对一次底面回波或二次底面回波的频谱特征参数进行分析时，试件与耦合剂的耦合情况、试件的表面粗糙度、上下表面的平行度以及系统噪声等都会对测量结果产生影响，从而降低了该方法的检测精度和工程中的适用性。

为解决传统频谱分析法存在的不足，本工作提出了基于频谱能量的材料晶粒度表征方法。首先，对超声信号的第一次和第二次底面回波分别进行频谱分析，获得频谱包络面积，此面积的大小反映了超声回波频谱能量强弱；然后，利用包络面积来计算超声波的衰减系数；最后通过衰减系数对材料的平均晶粒尺寸进行表征。新方法的优势在于：频谱能量可以较全面地反映超声回波所携带的信息，且对待测试件的表面粗糙度和上下表面的平行度要求低，受系统噪声干扰小，可以有效提高表征材料晶粒度的准确性。以奥氏体不锈钢材料为研究对象，通过不同的热处理方式获得不同晶粒尺寸的试件，分别对每个试件进行超声检测后，再用衰减法、声速法以及新提出的频谱能量法对试件的平均晶粒尺寸进行表征。

1 方法的原理及步骤

对分析的试件进行超声检测，可以获得如图1所示的超声A-scan信号，分别截取超声一次底面回波x1(t)和二次底面回波x2(t)，然后按照图2所示的流程计算基于频谱能量的衰减系数α1，其中L为试件的厚度。

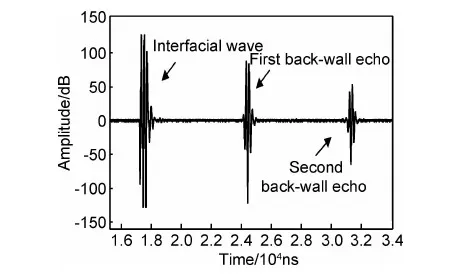
图1 超声A-scan 信号Fig.1 Ultrasonic A-scan signal

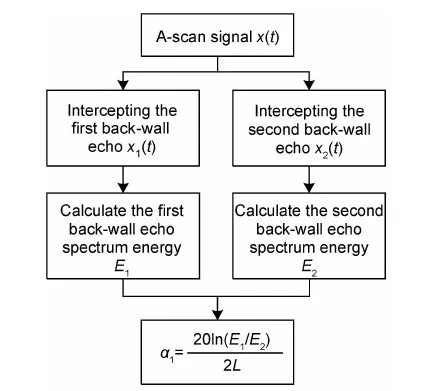
图2 算法流程图Fig.2 Algorithm flow chart

具体的计算流程：

(1)信号时频转换。对超声底面回波信号xi(t)进行傅里叶变换，得到对应的频谱信号Xi(f)。其中，i=1，2表示第一次和第二次的底面回波对应的编号，t1和t2分别为傅里叶变换的积分上下限。

(1)

(2)

(3)

根据Hilbert变换的性质，复信号yi(t)的模即为原信号的包络：

(4)

进一步将时域的包络转换为频域的包络，可表示为：

(5)

(6)

式中f2与f1分别为信号频谱的积分上下限。

(4)计算基于频谱能量的衰减系数。在式(6)中取i=1,2，所得到的E1，E2分别代表第一次，第二次超声底面回波的频谱能量，参照传统衰减法的计算公式，可以得到基于频谱能量的衰减系数α1：

(7)

计算得到的衰减系数α1可以看作是材料晶粒尺寸表征的超声特征参数，通过拟合衰减系数α1与材料平均晶粒尺寸的关系曲线来预测材料的晶粒度。

2 实验与讨论

2.1 制样及金相测量

实验对象为304奥氏体不锈钢，牌号为0Cr18Ni9。该材料在常温下为奥氏体组织，热处理后材料不会发生相变，一般为等轴多边形晶粒。在加热到1000～1200℃过程中，材料的晶粒尺寸不断增大。由于晶粒长大的程度与热处理的温度以及保温时间有关，温度越高且保温时间越长，则晶粒长得越大。制备规格为φ30mm×20mm的奥氏体不锈钢试件11个，利用快速升温箱式电炉分别对试件进行不同的热处理，以期获得不同晶粒尺寸的试件。具体热处理工艺如表1所示。

表1 热处理工艺

将热处理后的各试件去除表面氧化皮，再进行打磨、抛光，然后使用“王水”腐蚀，最后将处理好的试件放在金相显微镜下观察，保存具有代表性区域的金相图。按照GB/T6394-2002《金属平均晶粒度测定方法》对各试件平均晶粒尺寸进行统计，将统计的结果取平均值作为试件最终的平均晶粒尺寸的参考值。2#试样和10#试样的显微组织如图3所示，材料晶粒尺寸的统计结果如表2所示。可以看出，通过不同的热处理过程，试件的平均晶粒尺寸发生了明显的变化，从原来的22.56μm长大到176.08μm。

图3 2#试件(a)和10#试件(b)的显微组织Fig.3 Microstructures of No.2# sample(a) and No.10# sample(b)

SampleNo．1#2#3#4#5#6#7#8#9#10#11#Averagegrainsize/μm22．5657．9678．6983．13107．77120．81137．28153．49140．76167．11176．08

2.2 超声检测

检测设备采用SAM-300水浸超声系统，采样率1GHz，探头为5MHz平探头。为保证表征晶粒度的准确性，对每一个试件都随机寻找30个位置进行超声检测，然后将检测的结果进行平均处理，以此来代表超声检测的最终结果。为与传统方法进行对比，分别按式(8)，(9)计算得到衰减系数α2和声速v:

(8)

(9)

式中：A1和A2为超声信号的第一次和第二次底面回波幅值的最大绝对值；Δt为两次回波的时间差。需要说明的是，新方法所得到的衰减系数α1是通过计算两次底面回波的频谱能量得到的，而传统的衰减系数α2是基于两次底面回波的幅值得到的。分别计算出各试件对应的α1，α2，v三个声学特征参数，统计结果如表3所示。

表3 声学特征参数统计结果

由于对每个试件都进行了30个位置点的超声检测，因此在表3中列出的是声学特征参数的统计平均值。为评价新方法对材料晶粒度表征的适用性，将11个试件分为两组：拟合数据组和预测数据组。其中，4，7，10#试件为预测数据组，分别代表了小、中、大三个不同的晶粒尺寸；剩余的8个试件则作为拟合数据组。

根据前人研究结果可知[15]，在典型的多晶固体中，由波长与平均晶粒尺寸的关系，可将材料内部的散射过程分为如下三种类型：

(10)

(11)

(12)

式中：F为各向异性系数；C2，C3，C4为常数。根据实验条件可知，检测频率为5MHz，试件中最大的平均晶粒尺寸为176.08μm，对于11个试件，波长与平均晶粒尺寸均满足λ≫πD，即满足公式(10)的关系，因此材料内部的散射都属于瑞利散射过程。此外，从公式(10)可以看出，衰减系数与平均晶粒尺寸满足高次非线性关系。因此，在数据拟合的过程中，以金相测量所得到的平均晶粒尺寸为参考值，利用多项式方程来分别拟合α1，α2，v三个声学特征参数与晶粒尺寸参考值D之间的关系，拟合结果如图4和图5所示。

图4 衰减系数-平均晶粒尺寸的拟合结果Fig.4 Fitting results of attenuation coefficient and average grain size

图5 声速-平均晶粒尺寸的拟合结果Fig.5 Fitting results of velocity and average grain size

从图4中可以看出，材料平均晶粒尺寸增大时，超声波衰减系数α1和α2都增大。这是因为，随着平均晶粒尺寸的增大，材料的各向异性程度加大；另外在瑞利散射区，材质晶粒粗大会使散射衰减加剧，因此晶粒尺寸越大，衰减系数越大。利用复测定系数R2[16]来评价曲线拟合的效果。当R2=0时，表示拟合的方程完全不能解释原数据的特征；当R2=1时，则说明拟合的方程与原始数据完全吻合。由此可见，R2越大，则拟合方程具有越强的逼近能力。在图4中，基于频谱能量计算得到的衰减系数α1与晶粒尺寸参考值之间的复测定系数为0.9925，而基于幅值计算得到的衰减系数α2与晶粒尺寸参考值之间的复测定系数为0.9846，说明新方法得到的方程能更好地描述衰减系数与晶粒尺寸之间的关系。

从图5中可以看出，材料平均晶粒尺寸增大，超声波声速有减小的趋势。这是因为奥氏体不锈钢在1000～1200℃的加热过程相当于是固溶处理，此时合金元素铬、镍取代铁原子的位置而形成置换固溶体。随着加热温度升高，或同一温度下，增加保温时间，固溶体增加，引起晶格畸变，使原子之间的结合力下降，弹性模量降低，从而造成声速减小。因此，晶粒尺寸越大，声速越小。此时得到的复测定系数为0.8593。

利用拟合好的方程分别对4，7，10#试件进行晶粒尺寸的预测，结果如表4所示。

表4 晶粒尺寸预测结果

从表4中可以看出，频谱能量法对三个试件晶粒尺寸的预测误差均小于衰减法和声速法的预测误差。具体来说，频谱能量法的预测误差控制在4%～15%以内，而衰减法的误差最大达到17.2%，声速法的预测误差最大为57.25%，说明新方法比传统方法具有更高的检测精度。

2.3 数据波动性的讨论

新方法本质上也是一种衰减法，比较两种衰减法所得到的衰减系数α1和α2对数据的敏感程度，以此来评价方法的鲁棒性。在上述实验中，每个试件都分别取了30个不同的位置点来进行超声检测，因此对于同一个试件，则可以对应获得30个衰减系数，然后再计算这30个衰减系数的标准差。标准差衡量的是样本数据的离散程度，标准差越小，说明数据的稳定性越好，计算结果如图6所示。

图6 标准差比较Fig.6 Comparison of standard deviation

从图6中可以看出，当晶粒尺寸较大时，两种方法的标准差也相对较大，这是因为：材料的平均晶粒尺寸越大，晶粒的不均匀性越严重，散射越剧烈，从而增大了数据的波动性，表现为衰减系数的标准差增大。此外，对于11个试件，基于频谱能量的衰减系数α1的标准差均小于传统衰减系数α2的标准差，说明新方法的鲁棒性更好，抗干扰性更强。这是因为：将超声底面回波转换到频域进行分析，实质是把信号在频域内进行了均值化处理，使得随机噪声在频域内被弱化，在此基础上，再利用频域的包络面积来整体反映超声信号的能量大小，可以进一步减少噪声对计算结果的影响；而传统的衰减法只是关注某个数据点，即超声底面回波时域波形中的最大幅值点，更容易受到噪声等因素的影响。

3 结论

(1)基于频谱能量的材料晶粒度表征方法，是利用两次底面回波的频谱能量的衰减来表征材料的晶粒尺寸大小，可以更全面地反映超声信号所携带的特征，在一定程度上可有效克服系统噪声所带来的影响，数据波动性小，检测结果更可靠。

(2)频谱能量法得到的衰减系数与平均晶粒尺寸呈非线性关系，与传统衰减法相比，新方法得到的拟合关系曲线的复测定系数更高，预测误差可控制在4%～15%以内。

(3)在实际应用过程中，可将频谱能量法与衰减法、声速法有机结合，以得到更优的声学特征参数，将有利于进一步提高材料晶粒度表征的准确性。此外，在对小晶粒尺寸的材料进行预测时，需要提高探头的频率，并增加小晶粒尺寸的试件数来参与建模，以提高预测精度。

[1]SUNDINS,ARTYMOWICZD.Directmeasurementsofgrainsizeinlow-carbonsteelsusingthelaserultrasonictechnique[J].MetallurgicalandMaterialsTransactionsA,2002,33(3):687-691.

[2]MILITZERM,MOREAUA,MAALEKIANM.Laser-ultrasonicaustenitegrainsizemeasurementsinlow-carbonsteels[J].MaterialsScienceForum,2012,715:407-414.

[3] 张婷，刘奎，王婷婷. 复合材料修理结构的缺陷特征与超声信号[J]. 航空材料学报,2015,35(1):66-70.

ZHANGT,LIUK,WANGTT.Defectcharacteristicsandultrasonicsignalofcompositerepairstructure[J].JournalofAeronauticalMaterials,2015,35(1):66-70.

[4]PAPADAKISEP.Ultrasonicattenuationandvelocityinthreetransformationproductsinsteel[J].JournalofAppliedPhysics, 1964,35(5):1474-1482.

[5]KOPECB,HANAKV.Usingultrasonicattenuationmeasurementstoinvestigateanomaliesinthestructureofrailwayaxles[J].NDTInternational,1984,17(5):265-268.

[6]BOUDAAB,LEBAILIS,BENCHAALAA.Grainsizeinfluenceonultrasonicvelocitiesandattenuation[J].NDT&EInternational,2003,36(1):1-5.

[7] ÜNALR,SARPÜNIH,YALIMHA,etal.Themeangrainsizedeterminationofboroncarbide(B4C)-aluminium(Al)andboroncarbide(B4C)-nickel(Ni)compositesbyultrasonicvelocitytechnique[J].MaterialsCharacterization,2006,56(3):241-244.

[8]AGHAIE-KHAFRIM,HONARVARF,ZANGANEHS.CharacterizationofgrainsizeandyieldstrengthinAlSi301stainlesssteelusingultrasonicattenuationmeasurements[J].JournalofNondestructiveEvaluation,2012,31(3):191-196.

[9]PALANICHAMYP,JOSEPHA,JAYAKUMART,etal.Ultrasonicvelocitymeasurementsforestimationofgrainsizeinausteniticstainlesssteel[J].NDT&EInternational,1995,28(3):179-185.

[10] 陈建忠, 史耀武. 低碳钢晶粒尺寸的超声无损评价技术[J]. 无损检测,2002,(9):391-394.

CHENJZ,SHIYW.Ultrasonicnondestructiveevaluationofthegrainsizeoflowcarbonsteel[J].NondestructiveTesting,2002,(9):391-394.

[11]SHARMAGK,KUMARA,RAOCB,etal.ShorttimeFouriertransformanalysisforunderstandingfrequencydependentattenuationinausteniticstainlesssteel[J].NDT&EInternational,2013,53:1-7.

[12] 张洪达，马世伟.Cr-Mo钢平均晶粒尺寸的超声无损评价[J]. 上海大学学报(自然科学版),2006,(2):162-165.

ZHANGHD,MASW.UltrasonicnondestructiveevaluationofaveragegrainsizeofCr-Mosteel[J].JournalofShanghaiUniversity(NaturalScienceEdition),2006,(2):162-165.

[13]BOUDAAB,ALJOHANIMS,MEBTOUCHEA,etal.Characterizationofgrainssizebyultrasounds[J].KeyEngineeringMaterials,2011,(482):49-56.

[14] 李萍，程向梅，李安娜，等. 304不锈钢固溶产物晶粒尺寸的超声无损表征研究[J].材料工程,2013,(6):77-81.

LIP,CHENGXM,LIAN,etal.Ultrasonicnondestructivecharacterizationofaveragegrainsizein304stainlesssteelsolutiontreatmentproducts[J].JournalofMaterialsEngineering,2013,(6):77-81.

[15]PAPADAKISEP.Ultrasonicattenuationcausedbyscatteringinpolycrystallinemedia[J].PhysicalAcoustics,2012,4:269-328.

[16] 王惠文，吴载斌，孟洁. 偏最小二乘回归的线性与非线性方法[M]. 北京：国防工业出版社,2006.

Characterization Method of Materials Grain Size Based on Spectrum Energy

LI Min1，ZHOU Tong1，WANG Shan-chao1， XIAO Hui-fang2，XU Jin-wu1

(1 School of Mechanical Engineering，University of Science and Technology Beijing，Beijing 100083,China；2 National Engineering Research Center of Flat Rolling Equipment，University of Science and Technology Beijing，Beijing 100083,China)

A method to characterize the grain size of the material by the spectrum energy of ultrasonic signals was proposed. In order to study the new method, firstly, some austenitic stainless steel materials with different grain sizes were prepared by different heat treatment regimes. Then the grain sizes of those prepared materials were characterized by using the attenuation coefficient, velocity and spectrum energy, respectively. The results show that attenuation coefficient calculated by the proposed method and the average grain size exhibit nonlinear relationship. The predicted error of the grain sizes is within 4%-15%, which is superior to the conventional methods, and verifies the effectiveness of the proposed method

ultrasonic detection；grain size；attenuation coefficient；velocity；spectrum energy

10.11868/j.issn.1001-4381.2015.12.012

TG115.28

A

1001-4381(2015)12-0069-06

北京高等学校青年英才计划资助项目(YETP0373)；“十二五”国家科技支撑计划资助项目(2012BAF04B02)

2014-09-24;

2015-04-21

黎敏(1980—)，女，副教授，主要研究方向为超声无损检测、信号处理与模式识别，联系地址：北京科技大学机械工程学院(100083)，E-mail:limin@ustb.edu.cn