基于雅克比矩阵的并联机构结构参数优化设计

魏永庚,袁 明,石 勇,盛遵冰,王中鲜

(1.黑龙江大学 机电工程学院，哈尔滨 150080；2.哈尔滨工程大学 动力与能源学院，哈尔滨 150001)

基于雅克比矩阵的并联机构结构参数优化设计

魏永庚1,袁 明1,石 勇2,盛遵冰1,王中鲜1

(1.黑龙江大学 机电工程学院，哈尔滨 150080；2.哈尔滨工程大学 动力与能源学院，哈尔滨 150001)

并联机构作为一种空间机构，其结构参数多，机构设计复杂，而且结构参数的改变会直接影响机构的运动精度，因此设计出合理的结构参数，成为并联机构结构设计的关键问题。以三平动并联机构为研究对象，提出一种基于雅克比矩阵的并联机构结构参数优化设计的方法。首先根据并联机构的结构形式推导出动平台的数学模型并建立雅克比矩阵，然后根据并联机构雅克比矩阵中的条件数性能评价指标，利用MATLAB软件对已知工作空间的并联机构结构参数进行优化仿真分析，最后优化出合理的结构参数。

三平动并联机构；结构参数优化；雅克比矩阵

0 引 言

并联机构一种普遍构型是由可变长度的驱动杆通过运动副将定平台和动平台连接起来的，改变驱动杆的长度，则引起动平台位姿的改变，可以进行各种运动模拟和仿真，三平动并联机构三维模型见图1。并联机构由于其无累积误差、自身负荷小、动态响应好和承载能力大等优点，而被广泛应用于高精度或者高速度场合中[1-3]。在对机构性能的分析中，并联机构的雅克比矩阵是评价并联机构运动性能的基础，也是衡量并联机床工作性能优劣的重要指标[4-6]。由图1可见，要计算动平台中心点的运动轨迹，需要知道定平台和动平台上运动副的铰链点在空间位置，定平台上3个铰链，每个铰链3个参数，动平台上3个铰链，每个铰链3个参数，总计6个铰链点18个参数，因此要测量出18个参数的准确坐标。由于实际加工、制造和装配的误差，18个参数的实际测量值不可能和理论值完全吻合，导致动平台的运动轨迹出现误差，无法保证机构的运动精度。

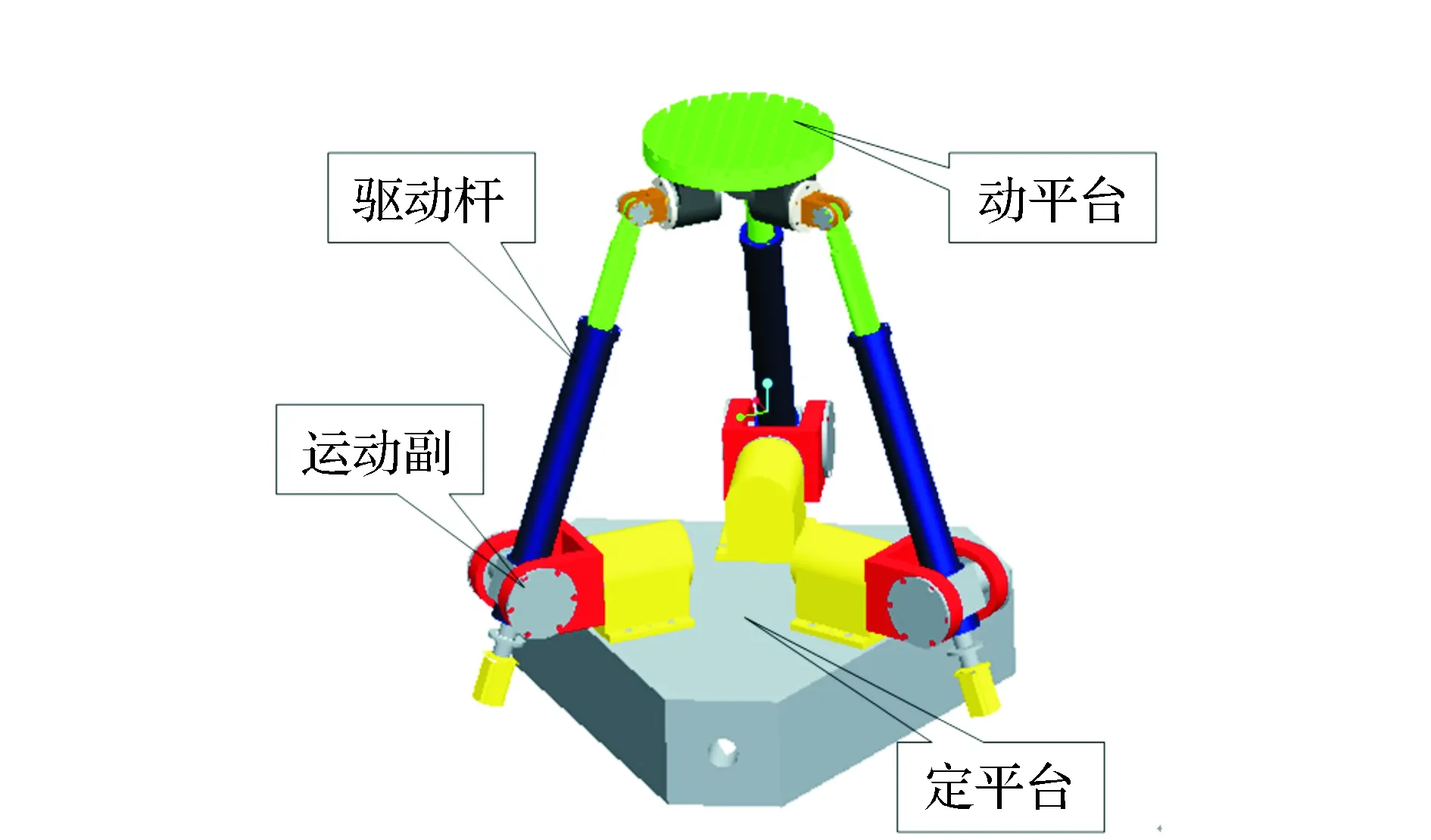
图1 三平动并联机构三维模型Fig.1 Three translation parallel mechanisms 3D model

目前，通常用雅克比矩阵的条件数[7-9]即雅克比矩阵的最大和最小奇异性的比值，作为并联机构精度的评价指标。本文以一种三平动并联机构为研究对象，利用Euler变换求解运动学正逆解，进而求出雅克比矩阵及其逆矩阵，利用雅克比矩阵的条件数指标和MATLAB软件对该机构的运动特性进行仿真分析，最终优化出合理的结构参数[10]。

1 三平动并联机构运动学求解

三平动并联机构的结构简图见图2，其中△A1A2A3和△B1B2B3是相似三角形，固定坐标系为Ob-XbYbZb，运动坐标系为Op-XaYaZa，Ob点为△B1B2B3的外接圆中心坐标，Xb坐标轴的正方向与B1B2同方向，Zb坐标轴垂直于XbOYb面且方向向上。考虑到初始状态，△A1A2A3的中心点Op映射到底面与△B1B2B3的中心点Ob重合，且各坐标轴指向均一致。

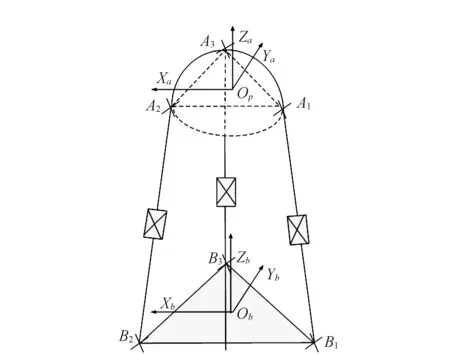
图2 并联机构简图Fig.2 Schematic diagram of parallel mechanism

通过齐次坐标变换推出运动学逆解公式(1)：

(1)

式中Op(px,py,pz)为运动平台中心坐标;R为固定平台半径;r为动平台半径;c=R-r为定动平台的半径之差;L1、L2、L3为3根驱动杆A1B1、A2B2、A3B3的长度。

式(1)描述了已知机构的动平台中心的位置和姿态，求解驱动杆长度变化的过程。通过式(1)又可推导出运动学正解如式(2)：

(2)

2 三平动并联机构的雅克比矩阵

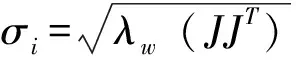
(3)

(4)

由以上可知雅克比逆阵J-1为式(5):

(5)

式(5)可进行并联机构的速度控制、奇异位形的判定、误差分析、轨迹规划以及灵巧性分析等。奇异性是当机构处于特殊位形时，机构的动平台将获得多余的不可控自由度或者失去部分自由度，并导致机构运动失控，这时的雅克比矩阵变成奇异阵，其行列式的值为零。

3 基于雅克比矩阵的并联机构性能分析

并联机构雅克比矩阵中的条件数性能评价指标，它不仅反映了机构离奇异位形的远近，速度方程的可解性，而且反映运动学性能和机构的静刚度特性。

3.1 条件数性能评价指标

机器人学常利用雅克比矩阵的奇异值构造3种评价指标：条件数指标、最小奇异值指标和可操作性指标。

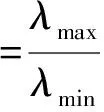
3.2 基于雅克比矩阵的条件数性能评价分析

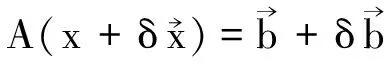
(6)

(7)

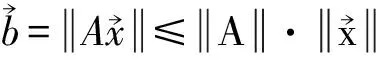
(8)

由式(7)和式(8)联立得出：

(9)

利用其条件数反映到并联机构上来，已知雅克比矩阵表示机构驱动杆输入速度L′到动平台输出速度p′的映射关系，即L′=J-1p′。也就是假设平台输出速度是精确的，当系数矩阵即雅克比矩阵求解发生微小偏差时，相应地导致杆长求解发生变化，进而导致机构运动不准确。

优化设计的基本原理：在给定的工作空间范围内，期望机构处在相对较小的E值范围内，需要对并联机构的结构参数进行优化，给出结构参数一定的取值范围，然后利用目标函数对其进行优化分析，通过在并联机构的工作空间内进行搜索，得到相对于此关键参数在整个工作空间内E的取值范围，得到各参数与E在此工作空间的变化图，查看其趋势，得到合理的参数值。

根据实验要求，已知运动平台的工作空间是直径150mm和高200mm的圆柱型区域，初步给出尺寸约束范围见式(10)，并对目标函数进行优化分析。

(10)

利用MATLAB软件对条件数E在不同关键参数影响下的变化情况进行分析。仿真结果见图3。图3主要分析了定平台半径、动平台半径以及二者之差及动平台中心点和条件数之间的关系。由图3 (a)可见，条件数E随动平台中心点X和Y的变化图像是一样的。在已知的工作空间[-150,150]的范围内，条件数E随动平台中心点X、Y坐标值的增加，先降低后增大且存在最小值。可见每种不同的的半径差对应的图像都是关于横坐标为0的轴线对称，且在x=0,y=0这个时刻条件数取最小。考虑到机构的合理性，这里选取c=600 mm，此时对应的条件数范围为1.58≤E≤1.72。由图3 (b)图可见随着半径差值的不断增大，条件数E关于动平台中心点Z坐标的图像逐渐向右平移，且都存在最小条件数值。通过得出的半径差和条件数范围读出对应的动平台中心点Z坐标值为670.8～870.8 mm。在条件为各杆长L=900 mm和已知动平台中心点Z坐标范围值时得出图3(c)图像。由图3(c)中可见，当动平台半径r和定平台半径R不断变大，其各自对应的条件数成相反趋势变化，但对应的半径差的条件数却不断地减小，最后趋近于稳定。因为第一个图已经知道最小条件数Emin=1.58，由图可见r=300 mm和R=900 mm，此时对应的半径差也为c=600 mm符合图3(a)结论。

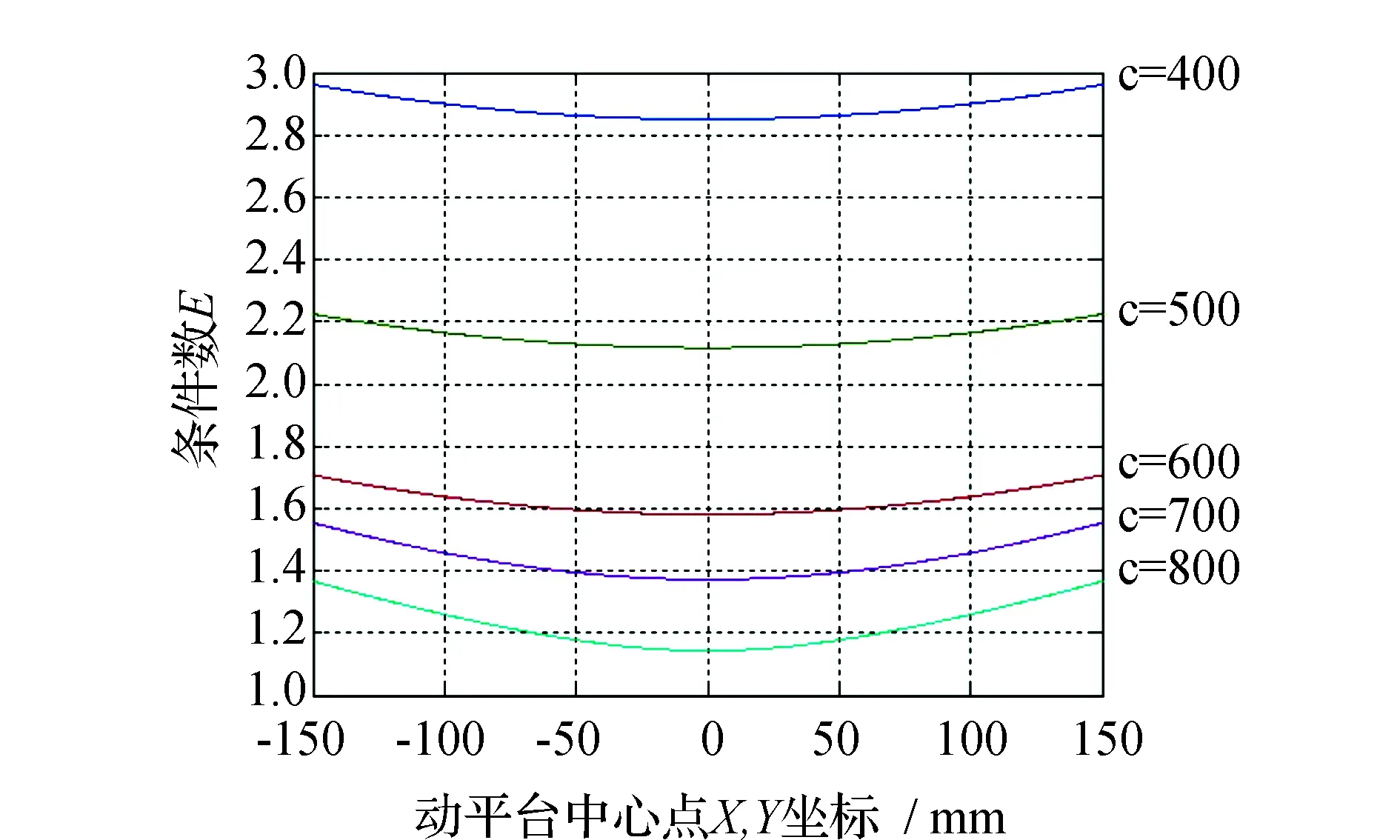
(a)动平台中心点X、Y的坐标与条件数E的关系

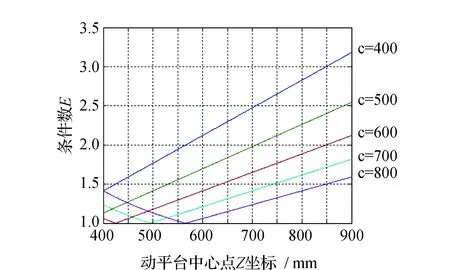
(b)动平台中心点的Z坐标与条件数E的关系

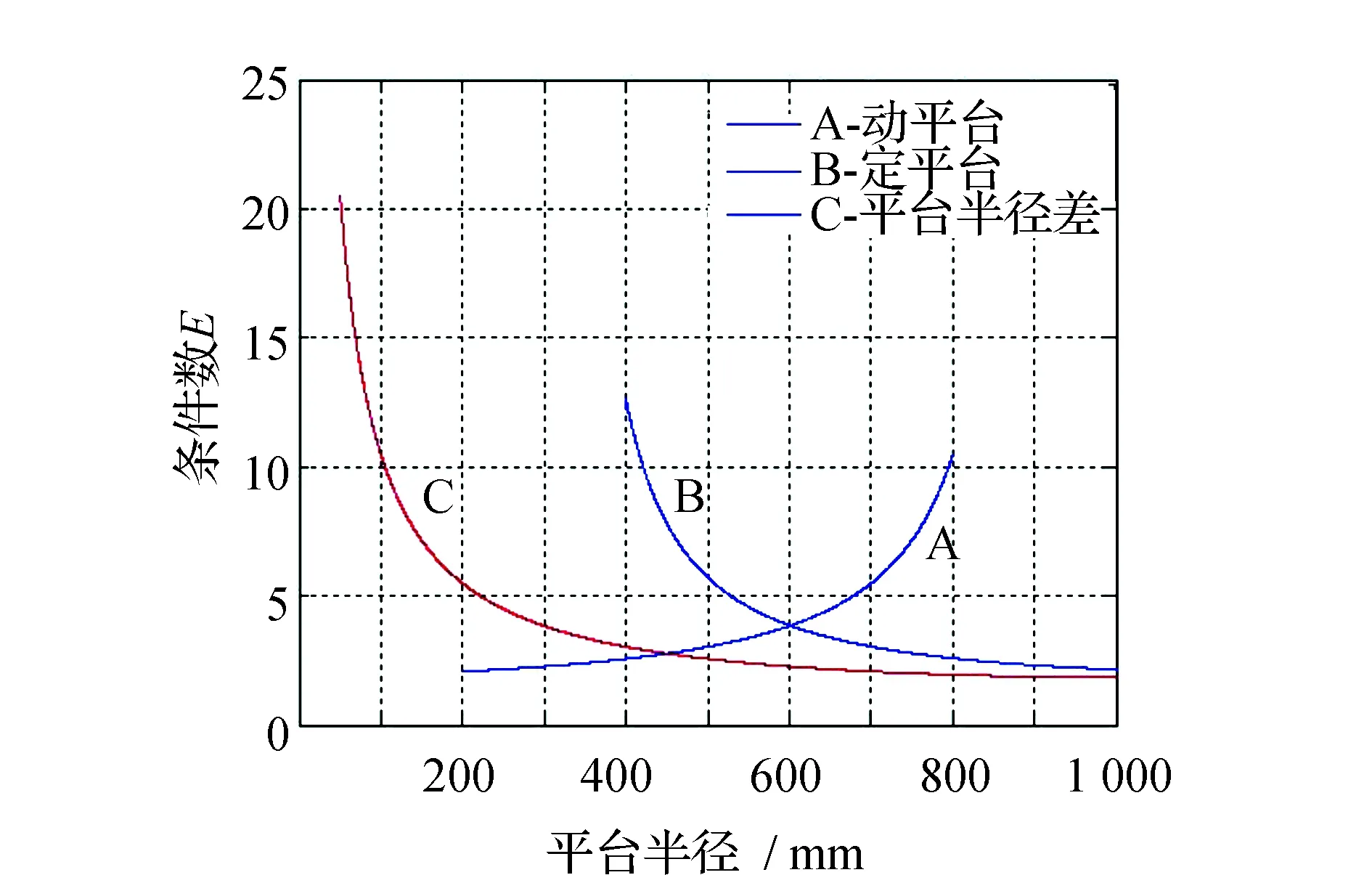
(c) 动平台半径、定平台半径及平台半径差与条件数E的关系图3 条件数分析Fig.3 Condition number analysis

已知机构的动平台△A1A2A3和定平台△B1B2B3为相似三角形，且初始状态△A1A2A3的中心Op映射到底面与△B1B2B3的中心Ob重

合,且各轴的指向均一致，令此时的中心点Op的垂直方向值为pz=670.8～870.8 mm，那么杆长可以表示为，经计算得出的结果与图像得出的完全一致。此时优化后的相关结构参数见表1。

表1 优化后的结构参数

4 结 论

通过对三平动并联机构的运动学性能分析可知，通过欧拉变换建立机构的矩阵模型可以清楚看出参数之间的关系，利用雅克比矩阵的重要性质，来讨论动平台中心点和结构参数的关系。利用Matlab和矩阵条件数性质，对并联机构关键参数进行优化，从中选取合适的条件数E的取值范围，使误差放大倍数在操作范围内值尽量小，最终确定并联机构的结构参数。

[1]高国琴,刘志慧,郑海滨.基于优化RBF神经网络的并联机器人位姿检测[J].机械设计,2012,(29):36-37.

[2]贾晓辉,刘今越.3-PRR柔性并联机构的优化设计[J].机械设计,2014,(31):27-29.

[3]Dallej T,Gouttefarde M,Andreff N,et al.Towards vision-based contril of cable-driven parallel robots[C]// in Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems,San Francisco,USA,2011:3 855-3 860.

[4]孙立宁,楚中毅,曲东升,等.2-DOF平面并联机器人结构参数优化的研究[J].哈尔滨工业大学学报,2004，(36):278-280.

[5]Ceccarelli M, Ottaviano E, Galvagno M.A 3-DOF parallel manipulator as earthquake motion simulator[C]// in Proc.7th.Conf.Control, Automation, Robotics Vision, Singapore, 2002：944-949.

[6]程世利,吴洪涛,王超群,等. 平面平台型Stewart并联机构的奇异性分析[J].机械工程学报,2011,47(9):2-6.

[7]姚 蕊,唐晓强,黄 鹏,等. 高加速度的柔性3-RRR并联机构尺度综合设计[J]. 清华大学学报：自然科学版,2008,48(2):184-188.

[8]Hunt K H. Structural kinematics of in-parallel-actuated robot-arms[J].ASME Journal of Mechanisms, Transmissions, and Automation in Design, 1983，105：705-712.

[9]Stock M, Miller K. Optimal kinematic design of spatial parallel manipulators:application to linear delta robot[J]. Journal of Mechanical Design,2003,125:292-301.

[10]曹 毅,黄 真,丁华锋,等. 6/6型Stewart机构姿态奇异及非奇异姿态工作空间分析[J].机械工程学报, 2005,41(8):50-55.

Structure parameters optimization design of parallel mechanism based on Jacobian matrix

WEI Yong-Geng1, YUAN Ming1, SHI Yong2, SHENG Zun-Bing1, WANG Zhong-Xian1

(1.School of Mechanical & Electrical Engineering, Heilongjiang University, Harbin 150080, China；2.School of Power & Energy, Harbin Engineering University, Harbin 150001, China)

The parallel mechanism’s feature are: a spatial mechanism, many structure parameters, mechanism design complex, and the change of structure parameters will directly affect the motion precision of mechanism. So the reasonable design of the structure parameters becomes a key problem of the parallel mechanism structure design. The structure parameters optimization design method of three translation parallel mechanisms is proposed based on Jacobian matrix. According to the structure style of the parallel mechanism, the mathematics model of the moving platform and the Jacobian matrix are deduced. And then, by the the condition number performance indices of the parallel mechanism Jacobian matrix, using the MATLAB software, optimization simulation analysis of the parallel mechanism structure parameters is conducted as known mechanism space. And finally, reasonable structure parameters are obtained.

three translation parallel mechanism; the structure parameters optimization; Jacobian matrix

10.13524/j.2095-008x.2015.01.017

2014-08-29

http://www.cnki.net/kcms/detail/23.1566.T.20150119.1617.003.html

黑龙江省教育厅科学技术研究项目 (12531520)

魏永庚(1972-)，男，吉林洮南人，副教授，研究方向：并联机构数控编程和结构设计,E-mail:wyg_1972@163.com。

TH122

A

2095-008X(2015)01-0087-05