永磁同步电机直接转矩控制系统建模与仿真

黄捷音，李光升，董今朝，谢永成

（1.装甲兵工程学院，北京100072；2.63978部队，河南 洛阳471099）

1 直接转矩控制的基本思想

直接转矩控制的基本思路［1］是，通过转矩两点式调节器把转矩检测值与转矩给定值作滞环比较，把转矩波动限制在一定的容差范围内，容差的大小由频率调节器来控制，因此，直接转矩控制的控制效果不取决于电机的数学模型是否能够简化，而是取决于转矩的实际情况。本文根据直接转矩控制思想，以永磁同步电机为载体构成一个具有良好动、静态特性的控制系统。永磁同步电机直接转矩控制系统如图1所示。

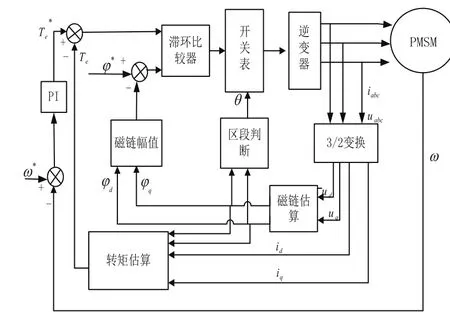
图1 永磁同步电机直接转矩控制系统框图

2 永磁同步电机数学模型

为了方便地得到定子电压、电流均为直流的永磁同步电机的电压方程式，本文对分析永磁同步电机控制过程系统的稳定性和动态性都采用在dq轴坐标系中建立永磁同步电机模型：

（1）电机在dq轴的定子磁链值［2］：

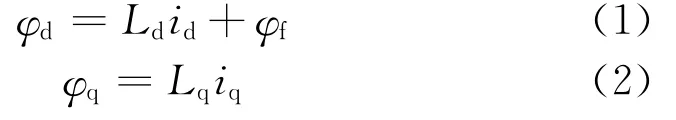
（2）电机在dq轴的电压表达式：

（3）电机的电磁转矩为：

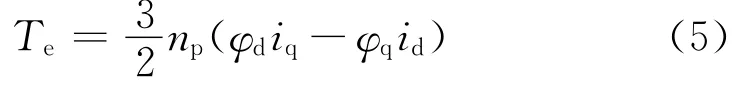
式中，φd、φq为定子磁链d、q轴分量；Ld、Lq为定子绕组d、q轴等效电感；id、iq为定子电流d、q轴分量；ud、uq为定子电压d、q轴分量；φf为转子磁链；Rs为定子绕组电阻；p为微分算子；ωr为转子机械角速度；Te为电磁转矩；np为电机极对数；Tm为负载转矩；J为电机转动惯量；B为粘滞系数。

（4）电机的运动方程：

3 仿真分析

在Matlab／simulink中建立永磁同步电机直接转矩控制系统仿真模型，如图2所示。

图2 PMSM直接转矩控制系统仿真模型

建立电机仿真模型后，对逆变器、磁链计算、转矩计算等建立仿真模型，如图3～图6所示。

图3 电机仿真模型

图4 逆变器仿真模型

图5 磁链计算仿真模型

4 仿真结果

设置电机参数：Ld＝0.641 m H，Lq＝1.952 m H，R＝7.5 mΩ，J＝2.97×10－3，np＝4，φf＝0.538 Wb，Te＝400 Nm，n*＝2 700 r／min，P＝120 kW，直流母线电压DC-BUS：750 V。设置系统初始参数给定转速ω*＝45 r／s，磁链给定值φ*＝1 Wb，开关频率f＝5×105Hz，电机的负载转矩为阶跃信号，进行仿真，得到仿真结果如图7～图9所示。

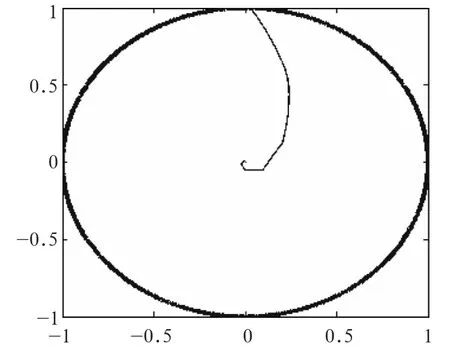
图7 磁链轨迹

图8 转矩曲线

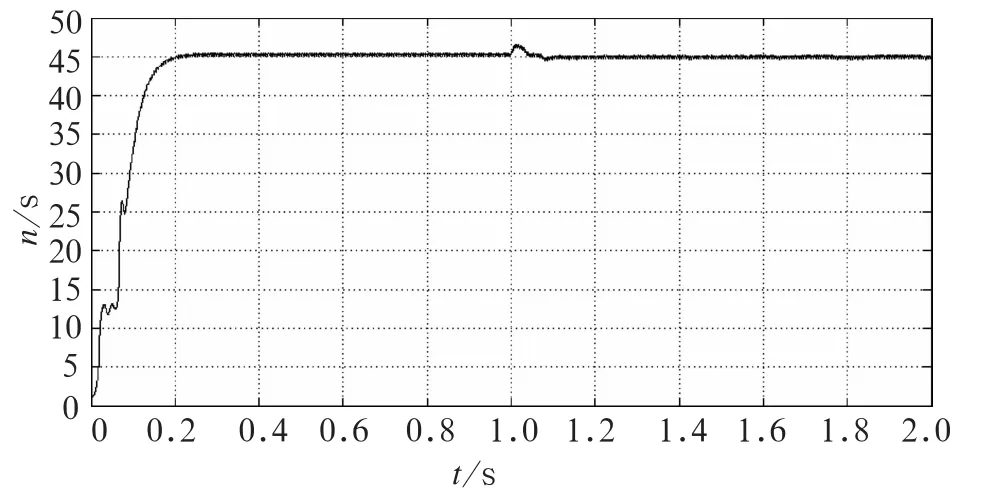
图9 转速曲线

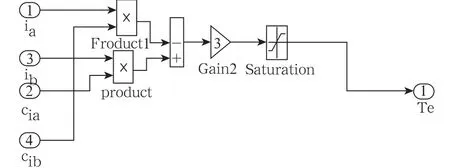
图6 转矩计算仿真模型

由图7可知，磁链轨迹收敛为圆形轨迹，图8可知，在t＝1 s时转矩由400 Nm跃变为300 Nm表现出很好的跟随性。从图9可知，转速响应较快，且超调量小，在恒定转矩下启动，最后转速稳定在额定转速2 700 rad／min，当t＝1 s时转矩由400 Nm跃变为300 Nm，电机转速出现一定的波动，但是最后转速依然稳定在给定转速。该控制系统的转矩响应迅速，表现出很大的抗干扰性，在此过程中磁链始终收敛成圆，负载转矩突变时，磁链已经建立起来了，达到额定之后磁链就保持在动、静上的近似恒定不变。而转矩很快地随动与负载转矩的变换，表现出了良好的动态特性和稳定性。

5 结束语

本文研究分析了永磁同步电机直接转矩控制系统在Matlab／simulink中的仿真模型，对某型电动车辆电机模型及其所需各模块模型进行仿真，通过仿真实验结果分析，验证了该方法结构简单、响应迅速、驱动状态稳定，具有一定实际意义。

［1］ 韩宝林.基于DSP的直接转矩控制系统研究与实现［D］.西安：电子科技大学硕士学位论文，2008.

［2］ 马小亮.高性能变频调速及其控制系统［M］.北京：机械工业出版社，2011.