功率因数可调的单相PWM整流器建模及控制系统设计

陆志杰，易映萍

（上海理工大学光电信息与计算机工程学院，上海200093）

0 引 言

随着电力电子技术［1］的飞速发展，电力电子变流装置已经广泛地应用于各行各业。目前，这些变流装置大都通过整流环节来获得稳定的直流母线电压。传统的整流技术［2］一般采用不控整流或相控整流方式，功率因数很低，会给电网带来大量的电流谐波和无功功率。为了满足功率因数、谐波及无功的标准，需要对电网谐波进行治理。目前谐波和无功功率治理的方法主要有无源电力滤波（PF）、有源电力滤波（APF）、静止无功补偿装置（SVC）、静止无功发生器（SVG）、PWM整流器等。与其他谐波抑制和无功补偿装置相比，PWM整流器是从源头上减少电网污染，因而是一种更好的谐波抑制和无功补偿方法。在中小功率场合，与一般PWM整流器相比，单相PWM整流器依靠相对低的成本及同样优异的性能，更具有竞争优势。本文采用一种新的建模方法——开关模型＋大信号平均模型，来对单相PWM整流器建模仿真。

1 单相PWM整流器建模

单相PWM整流器拓扑及开关模型如图1所示，四个IGBT单元在调制波高频调制下轮换导通。

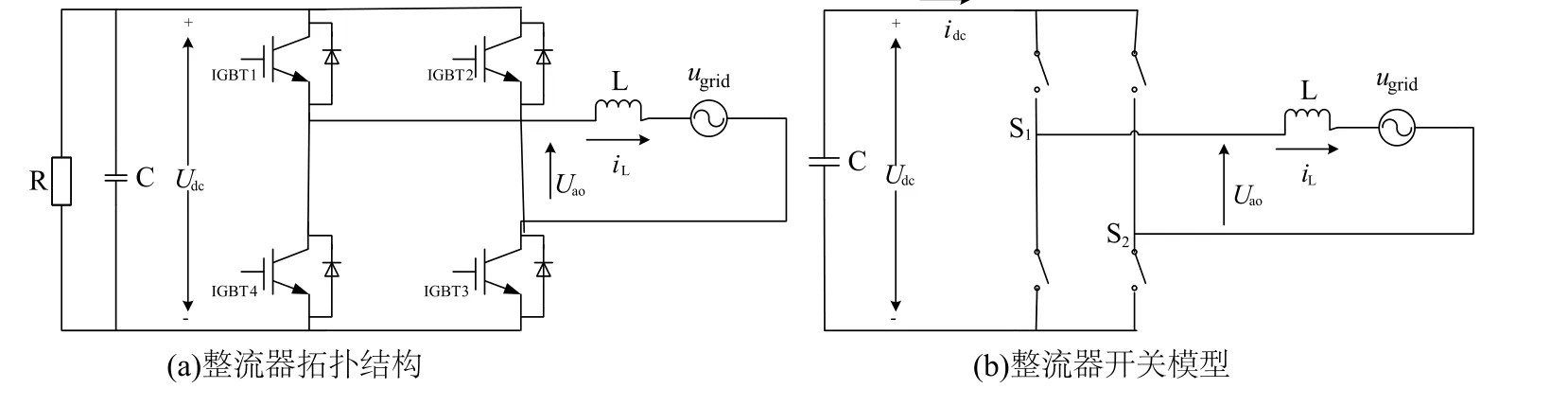
图1 单相H桥PWM整流器拓扑结构图及开关模型

设开关S1、S2在上桥臂导通时值为1，下桥臂导通时值为0，则其开关状态组合如表1所示。

根据表1可得：

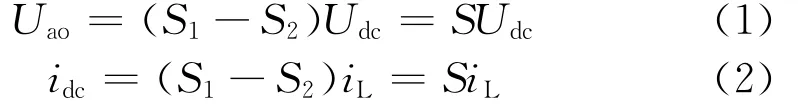
表1 S1、S2开关状态组合

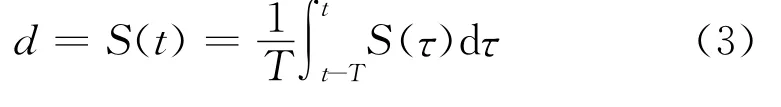
假设在一个开关周期中H桥整流器的直流电压Udc、交流输出电流iL均保持不变，则对式（1）、式（2）在一个开关周期进行平均，可得平均值为：

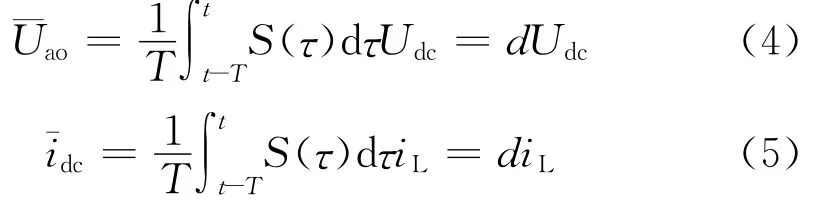
对开关函数S在一个开关周期中进行平均，由此可得平均值为：

对图1，由KCL、KVL及式（4）、（5）可得平均模型等效模型［3］如图2所示。由于逆变器输出为与电网同频、同相的交流信号，不存在稳态直流工作点，只有等效大信号平均模型，因此可直接根据图2所示大信号平均模型进行控制环路设计。

图2 大信号平均模型

2 单相PWM整流器控制器设计

整个H桥整流器控制系统由直流母线电压外环、电感电流内环［4］构成，控制环设计应遵从先内环，后外环的设计原则进行。控制框图如图3所示。

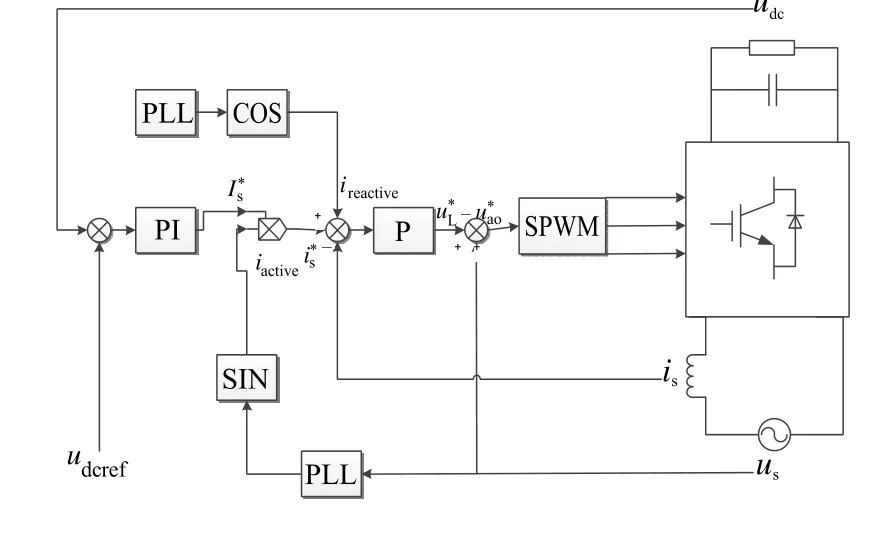
图3 功率因数可调的单相PWM整流器控制框图

不考虑无功功率控制，电感电流内环控制器控制目标为将电感电流控制为与电网电压同频、同相，在幅值上与指令值一致（即幅值上不能衰减）。为此可供采用的策略有三种：P调节器＋电网电压前馈控制；基于虚拟dq旋转坐标系下的PI调节器控制；PR调节器控制。综合考虑单片机或DSP资源、控制效果的快速性以及跟踪精度、控制算法的易实现性等因素，采用P调节器＋电网电压前馈控制为最优控制方案，电网电压前馈控制可抵消电网扰动，有利于提高电网瞬变扰动下整个系统的稳定性、同时降低电网谐波含量较大条件下受控电流的THD，P调节器则仅需微调电感电压。

因为PI调节器对正弦信号无法实现无静差控制，即整个系统是有差系统，且积分项的引入会导致控制量滞后，整流器交流端口输出电压与电网电压之间存在相位差，在电感上同时存在有功电流与无功电流，无法实现单位功率因数运行，故通常在单相PWM整流器控制系统中电流环较少采用PI调节器。而当采用电网电压前馈后，控制量不经过调节器延时，端口电压与电网电压几乎同相位抵消，P调节器则仅需微调电感电压，从而实现单位功率因数控制，故采用P＋电网电压前馈控制。

2.1 电感电流内环控制器设计

由图2所示大信号模型可得到采用P调节器＋电网电压前馈控制的等效控制结构图如图4所示。

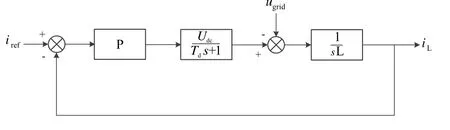
图4 电感电流内环控制结构框图

图中，Udc为H桥整流器直流母线电压；Td为控制系统等效延时；ugrid为电网电压扰动项。

由图2交流大信号平均模型可得受控电流对占空比的传递函数为：

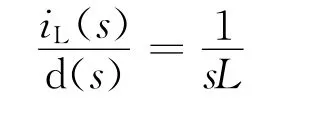
式中，L为滤波电感。

PWM最大延时为一个开关周期，等效传递函数为：

P调节器为：

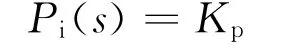
综合考虑延时环节后，由图4可得加入P调节器后开环增益函数为：

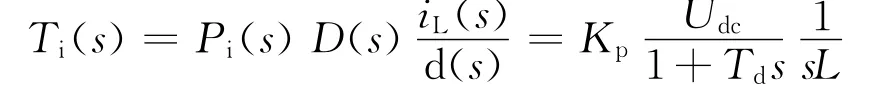
当考虑电流内环需要获得较快的电流跟随特性时，假设系统延时为半个开关周期，可以按照典型I型系统［5］设定参数：

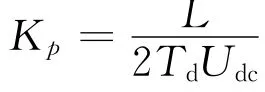
电网电压前馈控制只需实时采集电网电压，并将该值转换为调制度与电感电流环P调节器叠加即可（主要原因为电流环调节器输出进行了归一化处理，其范围为-1～1），具体在软件算法上，可将电网电压采样值与直流母线电压相除实现，即：

2.2 直流母线电压外环PI调节器设计

将电流内环闭环后的传递函数作为电压外环受控对象一部分，可近似等效为一阶惯性环节，根据功率平衡得到：

经近似处理后电压外环等效结构图如图5所示。

由于单相电路存在100 Hz功率波动，不可避免地会引起直流母线电压100 Hz波动，为对该电压2倍频成分进行衰减，避免引起并网电流中很大的三次谐波成分，可将电压采样信号延时1／4工频周期，再与延时前的相加，即可滤除100 Hz波动。

为保证对直流母线电压实现无差控制，电压环采用PI调节器。可得到电压环PI调节器参数如下：

电压外环控制环带宽设计为电流环的1／10。根据系统的开环传递函数可以计算在截止频率处系统的开环增益为1：

|Gvo（jw）|＝1，即可求得Kpu的值。

按照典型II型系统即可整定积分系数τu的值。

经PI校正后的电压环增益函数为：

3 功率因数的调节

为实现单相PWM整流器功率因数调节［6］，需要对无功电流进行控制，实现方式如下：

（1）首先通过过零比较电路得到电网相位信息，在单片机或DSP中生成正弦表，电网正向过零时触发捕获中断，将正弦表首地址也拉至与电网相位一致；

（2）功率因数为1时，交流电流相位与电网相位一致，无功电流指令为0；

（3）功率因数不为1时，将正弦表移相90°，再与给定无功指令电流幅值相乘即可得到无功电流；

（4）根据当前有功功率和需要调节的功率因数确定需要给定的无功电流幅值，如下式：

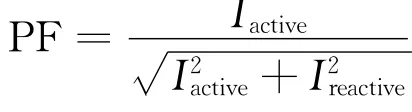
4 仿真及结果分析

为了验证本系统的控制策略，采用了Matlab／simulink对系统进行仿真［7］。仿真参数：电网频率50 Hz，直流侧电压Udc＝500 V，交流侧电压Ugrid＝220 V，直流母线电容C＝2 mF，交流侧滤波电感L＝2 m H，开关频率6.4 k Hz。

为了验证单相PWM整流器的性能指标，分别进行了电流内环仿真和电压外环仿真。simulink系统仿真如图6所示。

图6 simulink系统仿真图

4.1 电流内环仿真

电流环是双环控制的核心，也是整个系统设计的关键。为充分保证受控电流动态响应速度及在50 Hz处有足够的低频增益，同时兼顾对高频开关纹波的衰减特性，将电流内环带宽设置为1／6开关频率，即1 k Hz。在Matlab中利用sisotool工具对P调节器进环增益函数Ti（s）的Bode图如图7所示。由图7可知，在频率为1 k Hz处，相角裕度为81.1°，即电流内环是稳定的。

图7 经P调节器校正后电流环开环增益Bode图

在电流环稳定的情况下，不给无功电流指令时功率因数应为1。在0.3 s处给无功指令电流使功率因数为0.8。如图8所示，可知在0.3 s之前，电压电流波形同频同相，功率因数为1；在0.3 s时给无功电流指令后，电压电流波形错位，此时功率因数为0.8。从图8中可以看出，电流内环控制器使系统交流侧电流跟踪性能好，满足系统要求。

图8 交流侧电流电压波形（功率因数从1调到0.8）

4.2 电压外环仿真

电压外环的作用之一是稳定直流侧电压，在Matlab中利用sisotool工具对PI调节器进行设计，此时，Kpu＝0.32，τu＝0.1，经PI调节器校正后开环增益函数Bode图如图9所示。由图可知，此时相角裕度为77.7°，幅值裕度为58.7，即电压外环是稳定的。

图9 经PI校正后直流母线电压环开环增益函数Bode图

为了验证单相PWM整流器的电压外环设计的合理性，直流侧电压指令500 V，图10所示即为直流侧电压输出波形，可以看出响应时间以及超调都很小，电压很稳定，验证了电压外环设计是合理的。

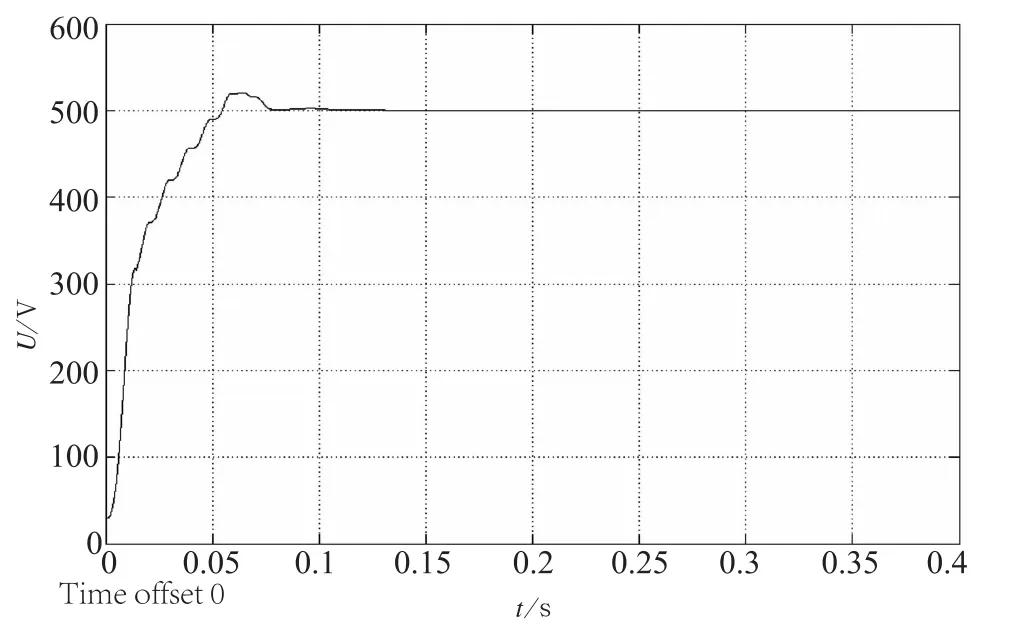
图10 直流侧电压波形

5 结 论

本文主要建立了单相PWM整流器的数学模型，设计了系统控制器，最后通过仿真进行了验证。可以看出，电压外环能够有效稳定直流侧电压；并且电流内环实现了单位功率因数整流，功率因数可调；实现了电网电流正弦化。

［1］ 林渭勋.现代电力电子技术［M］.北京：机械工业出版社，2005.

［2］ 王兆安，黄 俊.电力电子技术［M］.北京：机械工业出版社，2000.

［3］ 张 阳，张军明，杜韦静.基于回转器的Buck变换器大信号建模［J］.电工技术学报，2011，（S1）：50-55.

［4］ 贺 博.单相PWM整流器的研究［D］.武汉：华中科技大学，2012.

［5］ 胡寿松.自动控制原理［M］.北京：科学出版社，2007.

［6］ Mokrytski B.Pulsewidth modulated inverters for AC motor drives［J］.IEEE Transaction 1967 IGA，1967，3：493-503.

［7］ 王忠礼，段慧达，高玉峰.Matlab应用技术——在电气工程与自动化专业的应用［M］.北京：清华大学出版社，2007.