黏塑性流体运动的二维浅水方程模拟

杨小宸，张庆河

(天津大学水利工程仿真与安全国家重点实验室，天津 300072)



黏塑性流体运动的二维浅水方程模拟

杨小宸，张庆河

(天津大学水利工程仿真与安全国家重点实验室，天津 300072)

摘 要：利用垂向平均浅水方程模型描述黏塑性流体的运动，并基于剪切流动区切应力分布与明渠均匀层流切应力分布相等的假定，推导了浅水方程中切应力项的摩阻系数表达式.建立了黏塑性流体运动平面二维非结构化网格数值模型，空间离散采用有限体积法显式求解，时间积分采用具有二阶精度的Runge-Kutta格式求解.数值模型模拟结果与已有黏塑性流体流动实验结果进行了比较，二者有较好的一致性.

关键词：黏塑性流体；二维浅水方程；摩阻系数；有限体积法；非结构化网格

淤泥质河口海岸地区，常常会在近底部形成一层具有流动性的高浓度含沙水体，当其浓度达到一定程度时就会形成浮泥.浮泥的存在对于港口航道淤积、河口海岸环境和港口管理等方面都有重要影响.因此，通过数值模拟描述浮泥的流动对于预测航道淤积和港口航道整治具有重要的意义.合理描述浮泥流动需要建立水体-浮泥双层运动模型，而其中的关键之处是如何描述底部浮泥的流动过程.

由于浮泥往往可以看作黏塑性流体[1]，因此，建立黏塑性流体运动模型来模拟近底部浮泥的运动具有实际意义.目前对于黏塑性流体的模拟包括求解N-S方程[2-8]、求解浅水方程[1,9-13]及其他方法[14].从浮泥运动的空间尺度看，由于浮泥主要集中于床面附近，其平面尺度远大于垂向尺度，因此，采用浅水方程求解浮泥运动是一种比较合理的方法.

采用浅水方程来描述黏塑性流体运动，需要通过方程中的摩阻项来体现黏塑性流体复杂流变特性的影响.Laigle和Coussot[1]、Martinez[12]通过相对剪切率和流变参数求解摩阻项.Odd和Cooper[9]、Winterwerp等[10]、Wang等[11]和Canestrelli 等[13]都是通过引入摩阻系数表示摩阻项，但其中摩阻系数的取值则往往由经验确定.因此，在采用二维浅水方程求解黏塑性流体运动的数值模型中，如何合理地确定摩阻系数仍是目前有待解决的问题.

为此，本文将在一定的假定条件下，依据黏塑性流体的流变方程，推导二维浅水方程中黏塑性流体层流运动的摩阻系数，以避免摩阻系数确定的经验性.在此基础上利用有限体积法，建立黏塑性流体运动平面二维数值模型，并进一步采用已有黏塑性流体流动实验数据对建立的模型进行验证.

1　黏塑性流体运动的平面二维浅水方程模型

1.1控制方程

黏塑性流体平面二维浅水方程模型的控制方程为质量守恒方程和动量方程，即

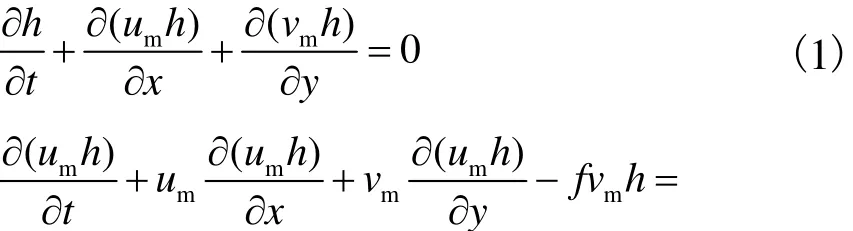
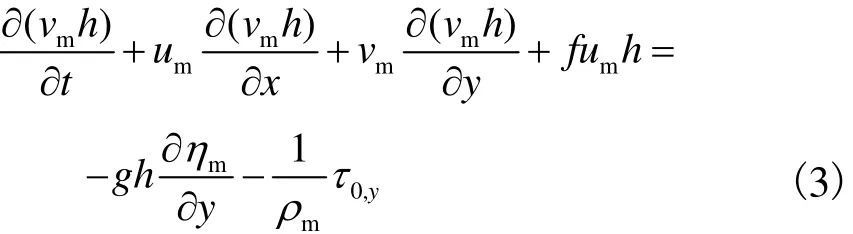
式中：um和vm分别为x和y方向流体的垂向平均流速；f为科氏力系数；g为重力加速度；hm为流体表面高程，hm=Z+ h ，其中Z为底床高程，h为流体厚度；rm为流体密度；t0,x和t0,y分别为x和y方向的底部摩阻应力，其表达式为

式中fm为摩阻系数.

如何合理地确定黏塑性流体的摩阻系数fm成为求解上述模型的关键.

1.2边界条件

黏塑性流体二维浅水方程模型的边界条件包括开边界条件、闭边界条件和动边界条件.开边界处可设定一定的流体厚度及施加一定的流量.岸线或建筑物边界可视为闭边界，流体可沿切向自由滑移，则闭边界的边界条件可表示为

式中：um为流体的速度矢量；n为固壁边界的外法线方向.

对于动边界的处理，采用干湿网格处理技术，干湿网格判断标准定义为：对于节点，h>0为湿节点，h≤0为干节点；对于三角形单元，max(hi,hj,hk)> 0为湿单元，max(hi,hj,hk)≤0为干单元，其中i、j和k分别为三角形单元的3个节点的编号.

1.3黏塑性流体摩阻系数的推导

已有研究表明，具有屈服应力的黏塑性流体在明渠中流动时，其流速分布在垂向存在整体向前均匀流动、没有相对剪切率的“流核区”，即在切应力等于屈服应力的屈服表面以上，为非剪切流核区，而屈服表面以下则为剪切流动区[15-16].为了推导黏塑性流体摩阻系数与平均流速的关系，这里近似假定剪切流动区切应力分布与明渠均匀层流切应力分布相等.

Herschel-Bulkley型黏塑性流体的流变方程为

式中：t为切应力；tB为屈服应力；K为黏度系数；n为流动指数；u为流体在各高度z处的速度；¶um,zm,z¶z代表剪切率.明渠均匀层流切应力分布为

式中J为水力坡度.则位于底部摩阻应力t0及位于屈服表面的屈服应力tB分别为

式中hB为屈服表面的高度，即切应力等于屈服应力的高度.根据剪切流动区切应力分布相等的假设，可推求剪切流动区流速沿垂向的分布为

在流核区，流动速度不随垂向高度变化，均为z=hB时的流速，即

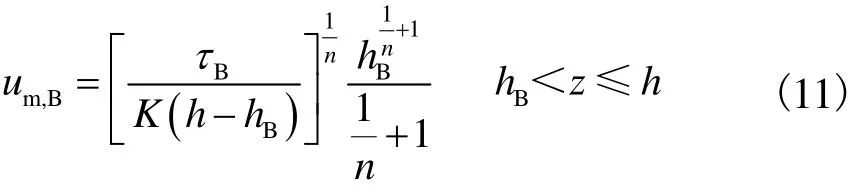
将流核区和剪切流动区的流速沿垂向积分，即得到沿垂向的平均流速um的表达式为

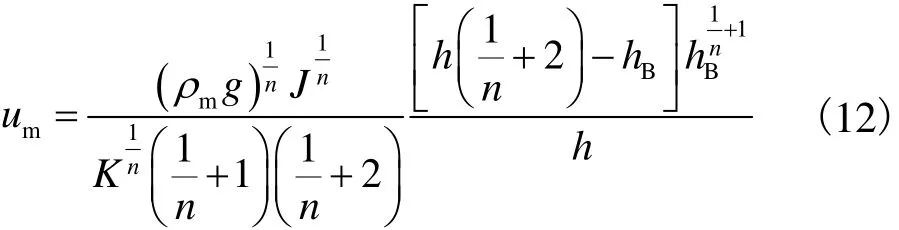
令Ne=tB/t0=(h- hB)/η ，则

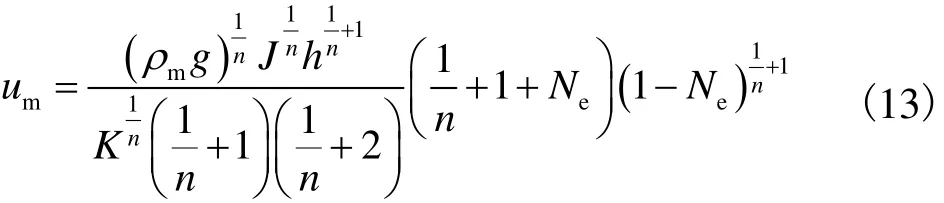
引入摩阻系数fm与底部摩阻应力0t的关系，又由式(8)可得

则可建立水力坡度与摩阻系数的关系为

根据，可得到

因此，当已知流变参数和平均流速时，通过式(16)和式(17)迭代求解，即可获得黏塑性流体的摩阻系数.

以上推导是以Herschel-Bulkley流变模型为例进行的，当黏度系数K取为宾汉体黏性系数h、n1=时，为宾汉流体，代入式(16)可获得宾汉体摩阻系数计算式

式中ReB为宾汉雷诺数，ReB=(rmumh )/η.式(18)与张道成[17]的宾汉体摩阻系数结果相同.

进一步，当屈服应力tB=0、K取为水的黏性系数m、n=1时，该流体变为牛顿流体.由于tB=0，则Ne=tB/t0=0，代入式(16)得到牛顿流体摩阻系数

式中Re为雷诺数，Re=(ρmumh )/μ.式(19)与文献[18]中的明渠水流层流摩阻系数公式吻合.

2　模型的数值离散

平面二维黏塑性体运动数值模型基于非结构化网格建立，空间离散采用有限体积法显式求解，时间积分采用Runge-Kutta格式求解.计算区域划分为若干无重合的三角形单元，如图1所示，每个三角形单元由3个节点(·)、3条边和一个单元中心(Å)组成.流体厚度h和表面高程mh等变量定义在节点上，流体流速um和vm等变量定义在单元中心上.

图1　三角形单元网格示意Fig.1 Illustration of triangular element mesh

首先对浮泥模型的质量平衡方程离散求解，在给定的三角形区域内积分，式(1)可写为

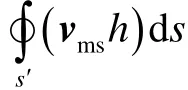
下面对动量方程(2)和(3)离散求解，在给定的三角形区域内积分，得到

将等式右侧各通量合并记为Ru和Rv，式(24)和式(25)可简写为

同样采用Runge-Kutta时间积分求解，得到

式中，XADV和YADV，PSTXM和PSTYM，CORX 和CORY，TAUX和TAUY分别为与式(24)和式(25)对应的对流项、流体表面压力梯度项、科氏力项和切应力项在x和y方向的分量.下面分别介绍各项的计算过程.对流项在x和y方向的分量分别表示为

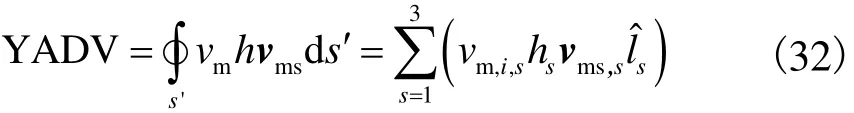
式中：um,i , s和vm,i , s分别为三角形单元边s中点处流体流速在x和y方向的分量；vms, s为垂直于该边的流体流速值，方向向外为正向；hs为该边中点处流体厚度值；为该边的长度.

流体表面压力梯度项在x和y方向的分量分别表示为

式中：Z为三角形单元边s中点处的底部高程；

sNi(j1)和Ni(j2)分别为边s的两端点的节点号.

科氏力项在x和y方向的分量分别表示为

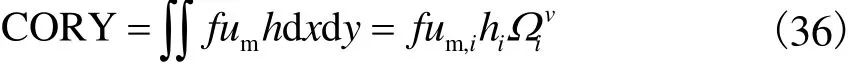
切应力项在x和y方向的分量分别表示为

式中t和t为流体摩阻切应力在三角形单元i中

0,x , i0,y , i心处的值，由式(4)计算得到.

3　模型验证

采用Cochard和Ancey[19]的黏塑性流体流动实验验证第2节建立的平面二维黏塑性流体运动模型.实验在可调节坡度的底坡上进行，底坡长5.5,m，宽1.8,m，顶端有长51,cm、宽30,cm的贮存池，对由不同浓度的卡波树脂U10(一种聚丙烯酸聚合物，具有增稠和流变改性作用)、NaOH和水组成的黏塑性流体进行了溃坝流动实验，采用CCD照相机测量流体自由表面的变化过程.实验所用的黏塑性流体的流变特性采用Herschel-Bulkley模型描述，并通过流变实验确定了参数.本文选取卡波树脂U10质量分数为30%、底坡坡度为6°的一组实验进行模拟，流体密度为811,kg/m3，实验布置[19]如图2所示.

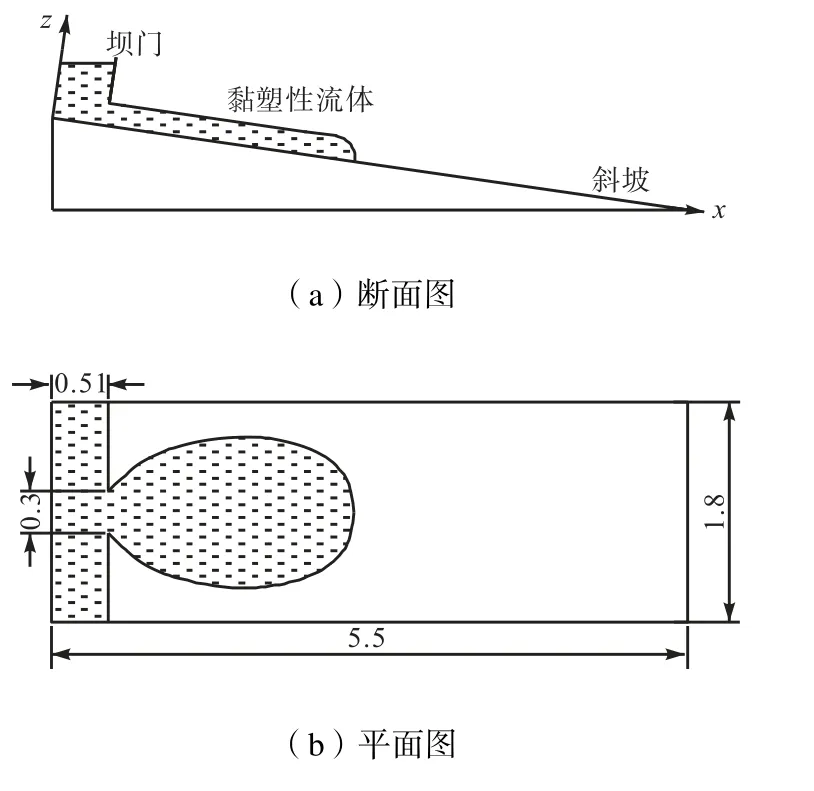
图2　实验布置图(单位：m)Fig.2 Lay-out of experiment(unit：m)

数值模拟计算区域长5.5,m，宽1.8,m，采用非结构化网格，最小网格尺度为0.05,m，计算时间步长为0.002,s.计算区域左右两侧设置为开边界，左侧入口边界根据实测数据设定不同时刻流体的高度并根据流入体积施加一定的流量，右侧为出流边界.流变实验确定的流变参数为tc=89 Pa ，K=47.68 Pa/sn，n=0.415，代入式(16)计算各时刻的底部摩阻系数，并应用本文建立的黏塑性流体运动模型模拟实验流体的运动.模拟得到的实验流体在各个时刻的流动厚度和流动边缘与实测数据的对比见图3和图4.模拟结果与实测结果较为接近，但由于本文的数值算法暂未模拟实际的溃坝间断问题，因此通过在左侧入口开边界施加不同时刻的流体高度以及根据实验时不同时刻的流入体积估算出的流量来设定入口边界，这与实验入口初速度不一定完全相同；另外，在实际流动中流体的表面张力可能也起到一定的作用，本文的模型中暂未考虑，因此计算结果与实测结果仍有一定的差异.

模拟中由式(16)计算得到的底部摩阻系数的值是随着实验流体的流动状态而变化的，本次计算中fm的值介于5～80之间.为了体现出本文所提出的底部摩阻系数确定方法的合理性，将本文的计算结果与fm取为定值(分别为fm=5、fm=60和fm=80)的情况进行对比.不同摩阻系数取值情况时实验流体前端位置及流动宽度与实测数据的对比分别见图5和图6.由图5可见，对于摩阻系数较小的fm=5情况，流体在2,s前基本能够符合实际流动结果，但之后流动较快，甚至在200,s时已达到计算域末端，与实测结果有较大差异.对于摩阻系数较大的fm=80情况，流动前沿位置始终小于实测结果；而摩阻系数fm=60的情况下，虽然在200,s时流动前沿位置基本与实测结果相符，但前期流动与实测结果相比仍较慢，只有摩阻系数由式(16)计算的情况下才能够较准确地描述出流体前端的位置.图6中流体宽度对比结果显示，除fm5=情况下流体宽度过大外，其他几种情况下流体宽度与实测结果均比较接近，可见摩阻系数对沿斜坡长度方向的流动的影响更明显.

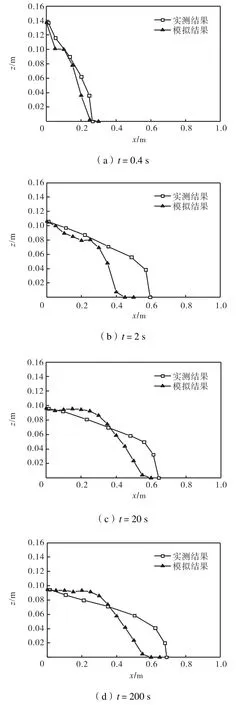
图3　不同时刻实验流体流动厚度模拟结果与实测数据对比Fig.3 Comparison of the simulated flow-depth and the measured data at different time

图4　 不同时刻实验流体流动边缘模拟结果与实测数据对比Fig.4 Comparison of the simulated flow-edge and the measured data at different time

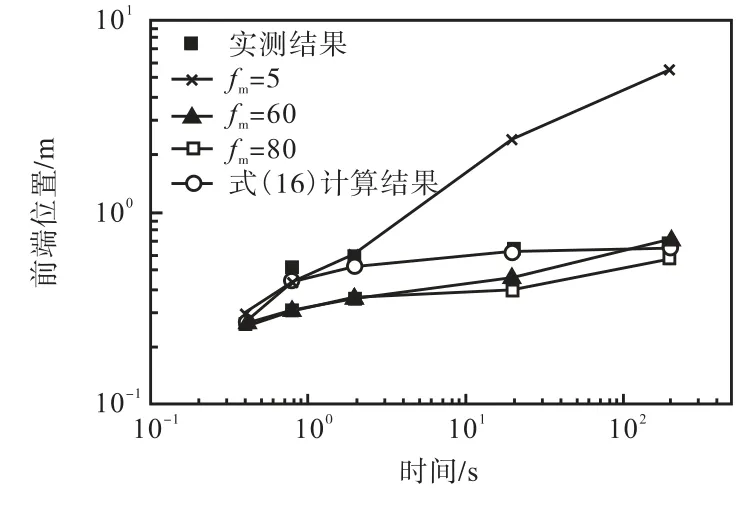
图5　不同摩阻系数时实验流体前端位置模拟结果与实测数据对比Fig.5 Comparison of the simulated front positions of the fluid and the measured data with different friction coefficients

图6　不同摩阻系数时实验流体流动宽度模拟结果与实测数据对比Fig.6 Comparison of the simulated widths of the fluid and the measured data with different friction coefficients

以上结果表明，本文的摩阻系数推求方法与摩阻系数经验性地取为定值相比，能更合理地描述黏塑性流体运动，同时模拟结果与实验结果的对比表明本文所建模型能够较合理地描述黏塑性流体的运动过程.

4　结 论

本文提出了一种黏塑性流体摩阻系数近似推求方法，并将其引入黏塑性流体的浅水方程中，建立了黏塑性流体平面二维运动模型.模型的求解基于非结构化网格，采用有限体积法进行数值离散.数值模型模拟与黏塑性流体流动实验结果比较表明，模拟结果与实测结果总体较为吻合，只是由于入口边界和表面张力等的影响在模型中尚未能充分合理考虑，二者相比还有一些差异.本文提出的摩阻系数近似推求方法与摩阻系数经验性地取为定值相比，模拟结果更接近实测结果，能够更合理地描述黏塑性流体的运动.

此外，需要指出的是，由于推导黏塑性流体摩阻系数时假设切应力与均匀层流切应力相符，本文模型一般仅适用于底坡较缓、黏塑性流体处于层流流动状态的问题.但总体来看，本文所提出的黏塑性流体摩阻系数推求方法避免了摩阻系数取值的经验性，可以进一步应用于河口海岸浮泥流动问题的研究中.为了进一步扩大模型应用范围，在以后的研究中将针对紊流情况进行改进，并与水流模型结合建立水流-浮泥双层模型，以期合理地描述河口海岸地区的浮泥运动.

参考文献：

［1］ Laigle D，Coussot P. Numerical modeling of mudflows[J]. Journal of Hydraulic Engineering，1997，123(7)：617-623.

［2］ Yan Y. Laterally-Averaged Numerical Modeling of Fluid Mud Formation and Movement in Estuaries[D]. Clemson：Department of Civil Engineering，Clemson University，1995.

［3］ Le Hir P，Bassoullet P，Jestin H. Application of the continuous modeling concept to simulate highconcentration suspended sediment in a macrotidal estuary[J]. Proceedings in Marine Science，2000，3：229-247.

［4］ Watanabe R，Kusuda T，Yamanishi H，et al. Modeling of fluid mud flow on an inclined bed[J]. Proceedings in Marine Science，2000，3：249-261.

［5］ Guan W B，Kot S C，Wolanski E. 3-D fluid-mud dynamics in the Jiaojiang Estuary，China[J]. Estuarine，Coastal and Shelf Science，2005，65(4)：747-762.

［6］ 马宗源，廖红建，张 骏. Bingham型黏性泥石流流体的三维数值模拟[J]. 西安交通大学学报，2008，42(9)：1146-1150. Ma Zongyuan，Liao Hongjian，Zhang Jun. Three dimensional numerical simulation of Bingham viscous debris flow fluid[J]. Journal of Xi’an Jiaotong University，2008，42(9)：1146-1150(in Chinese).

［7］ Knoch D，Malcherec A. A numerical model for simulation of fluid mud with different rheological behaviors[J]. Ocean Dynamics，2011，61(2)：245-256.

［8］ Minatti L，Pasculli A. SPH numerical approach in modeling 2D muddy debris flow[C]//Italian Journal of Engineering Geology and Environment，5th International Conference on Debris-Flow Hazards Mitigation，Mechanics，Prediction and Assessment. Padua，Italy，2011：467-475.

［9］ Odd N M V，Cooper A J. A two-dimensional model of the movement of fluid mud in a high energy turbid estuary[J]. Journal of Coastal Research，1989(SI5)：185-193.

［10］ Winterwerp J C，Wang Z B，van Kester J A Th M，et al. Far-field impact of water injection dredging in the Crouch River[J]. Proceedings of the ICE-Water and Maritime Engineering，2002，154(4)：285-296.

［11］ Wang L，Winter C，Schrottke K，et al. Modelling of estuarine fluid mud evolution in troughs of large subaqueous dune[C]//Proceedings of the Chinese-German Joint Symposium on Hydraulic and Ocean Engineering. Darmstadt，Germany，2008：372-379.

［12］ Martinez C E. Eulerian-Lagrangian Two Phase Debris Flow Model[D]. Miami：College of Engineering and Computing，Florida International University，2009.

［13］ Canestrelli A，Fagherazzi S，Lanzoni S. A massconservative centered finite volume model for solving two-dimensional two-layer shallow water equations for fluid mud propagation over varying topography and dry areas[J]. Advances in Water Resources，2012，40：54-70.

［14］ Hsu T J，Ozdemir C E，Traykovski P A. Highresolution numerical modeling of wave-supported gravity-driven mudflows[J]. Journal of Geophysical Research，2009，114(C05014)：1-15.

［15］ Mei C C，Yuhi M. Slow flow of a Bingham fluid in a shallow channel of finite width[J]. Journal of Fluid Mechanics，2001，431：135-159.

［16］ Yuhi M，Mei C C. Slow spreading of fluid mud over a conical surface[J]. Journal of Fluid Mechanics，2004，519：337-358.

［17］ 张道成. 宾汉流体在明渠均匀层流中的流变参数和阻力规律研究[J]. 成都科技大学学报，1990(1)：89-96. Zhang Daocheng. Preliminary study on the rheological parameters of Bingham fluid in laminar and uniform open channel flow[J]. Journal of Chengdu University of Science and Technology，1990(1)：89-96(in Chinese).

［18］ 李佳星，赵振兴. 水力学[M]. 南京：河海大学出版社，2001. Li Jiaxing，Zhao Zhenxing. Hydraulics[M]. Nanjing：Hohai University Press，2001(in Chinese).

［19］ Cochard S，Ancey C. Experimental investigation of the spreading of viscoplastic fluids on inclined planes[J]. Journal of Non-Newtonian Fluid Mechanics，2009，158(1/2/3)：73-84.

(责任编辑：樊素英)

Simulation of Viscoplastic Fluid Motion Through Two-Dimensional Shallow Water Equations

Yang Xiaochen，Zhang Qinghe
(State Key Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，Tianjin 300072，China)

Abstract：The motion of viscoplastic fluid was simulated using vertically averaged two-dimensional shallow water equations. The friction coefficient of the shear stress term in the equations was derived based on the assumption that the shear stress distribution of viscoplastic fluid in shear flow region equals to that of uniform laminar flow of Newtonian fluid in the open channel. A two-dimensional，unstructured-grid shallow water numerical model for viscoplastic fluid was developed. The explicit scheme of finite volume method was employed for the spatial dispersion，and the time integration was performed by the second order Runge-Kutta schemes. The model was validated by an experiment of viscoplastic fluid flow and the numerical results exhibit reasonable agreement with measured data.

Keywords：viscoplastic fluid；two-dimensional shallow water equations；friction coefficient；finite volume method；unstructured-grid

通讯作者：张庆河，qhzhang@tju.edu.cn.

作者简介：杨小宸（1986— ），女，博士研究生，daisy_yxc@126.com.

基金项目：国家自然科学基金创新研究群体科学基金资助项目(51321065)；教育部高等学校博士学科点专项科研基金资助项目(20120032130001).

收稿日期：2013-10-21；修回日期：2014-03-24.

DOI:10.11784/tdxbz201310056

中图分类号：TV148.1

文献标志码：A

文章编号：0493-2137(2015)06-0520-07