电力通信网络边扩充二分算法

杨 挺，袁 博，赵承利，吴 成，盆海波

(1. 天津大学电气与自动化工程学院，天津 300072；2. 天津市航海仪器研究所，天津 300131)



电力通信网络边扩充二分算法

杨 挺1，袁 博1，赵承利2，吴 成1，盆海波1

(1. 天津大学电气与自动化工程学院，天津 300072；2. 天津市航海仪器研究所，天津 300131)

摘 要：随着智能电网的发展，电力通信系统自动交换光网络(ASON)的网架结构日趋复杂，拓扑优化方法成为保证可靠通信、提升网络健壮性的首要关键技术.为此，对电力通信ASON网络拓扑优化问题建模，并提出一种以代数连通度为测度的网络边扩充优化二分算法.通过理论证明赋权图的拉普拉斯矩阵对应特征方程式的单调性，进而采用二分算法快速求解该单调非线性特征方程式的根，确定最优边扩充策略.仿真结果表明在链路失效时，网络边扩充优化二分算法能够以O(4mn lb(x/d))低复杂度找到精确解，降低端到端通信路径长度，提升网络效能函数.

关键词：电力通信网络；边扩充；二分算法；网络效能函数

网络出版时间：2014-03-24. 网络出版地址：http://www.cnki.net/kcms/doi/10.11784/tdxbz201401040.html.

电力通信网络是一个集多种业务子网的复杂网络系统，其传统组网方式采用同步数字传输(synchronous digital hierarchy，SDH)环网，而非通信逻辑上的网状结构，其优势在于SDH环网的高速自愈性能[1].随着分布式电源以微网形式接入，智能电网从结构到功率传输都发生了根本改变[2]，为满足高效可靠系统控制要求，电力通信网格形成了大量的SDH跨环业务，传统技术难以实现有效的QoS保证.自动交换光网络(automatic switched optical network，ASON)[3]以其特有的快速业务配置能力和抵抗网络故障等优点，成为解决当前SDH环网固有缺陷的有效方法.目前电力通信网络已经逐步建设形成以SDH环网为主、核心层采用ASON的融合网络.

ASON核心网络为网状结构，通过强劲的自动光路由技术实现不同类型业务的快速传输[4].因此网络结构的合理性直接决定了核心网络的健壮性、抗毁性和最大交换能力.如何在已有的网络结构基础之上进行最小代价的光纤建设，实现最大化网络收益，即最大化提升网络健壮性和抗毁性，成为当前智能电网通信建设中亟需解决的问题.对该问题进行理论研究并提出算法加以解决将对当前我国智能电网建设具有重要的意义.本文将电力ASON进行图论建模，抽象为赋权图，以代数连通度作为网络健壮性的测度，通过理论证明了赋权图的拉普拉斯矩阵对应特征方程式的单调性，进而提出一种适用于赋权图的二分边扩充算法实现快速求解该单调非线性特征方程式的根，确定最优边扩充策略.

本文分析了代数连通度作为测度对网络健壮性描述的准确性，并建立了ASON及其健壮性优化的数学模型；详细阐述了所提出的针对赋权网络边扩充二分算法，并采用不同规模的AOSN进行仿真分析，以评价算法的有效性和较优性.

1　相关工作

为实现光网络的智能化，ITU-T提出在光传送网中引入控制平面以实现网络资源的按需分配，ASON的概念应运而生[3].并随即开展了ASON的标准化工作，提出ASON的主要架构以及其演进策略——在SDH技术中逐步引入ASON技术.国家电网公司也在智能电网建设规划中指出：电力通信网的建设以SDH传输技术为主，同时积极跟踪和研究ASON等技术，构建ASON与SDH相融合的电力通信网络[5].

国内外学者对ASON在电力系统通信中的相关研究已经表明ASON的引入将有力提升SDH环网的可靠性和抵御故障能力.同时也提出了ASON在电力通信网络中仍然存在拓扑优化的核心待解决问题[6-13].Ma等[6]分析了ASON和SDH融合网络分层结构在安全和路由控制等方面的脆弱性情况，并且讨论了ASON的整体连通性问题.Albert等[7]建立了随机失效模型和恶意攻击模型，并分析了随机图模型网络在受攻击情况下的健壮性.这两种攻击模型成为研究网络健壮性常用的攻击模型.

针对网络中存在的健壮性问题，Beygelzimer等[8]发现网络可以通过修正或者增加一定的边来优化随机网络的健壮性，提升网络遭受攻击后的自愈能力.他们提出了6种策略，其中有2种边扩充策略，即随机节点对边扩充和最小度节点对边扩充方法，并以网络最小路径作为评价指标.

Kim等[9]提出了使用代数连通度作为动态网络提升健壮性的测度.Ghosh等[10]提出了利用贪婪式算法通过逐条加边的方式来找出具有最大代数连通度的边，直到满足实际性能要求的限制条件.Ibrahim 等[11]提出用半定规划技术来找到最优化的边.随后，Kim[12]提出了基于代数连通度的无权网络二分算法，该算法循环利用二分算法的思想来找出使得代数连通度最大化的边，实现拓扑网络的加边优化.然而，以上工作均是针对无权图的边扩充方法.当考虑到电力通信网络中每个通信节点的重要性差异，以及链路的费用、光衰耗、路径长度等因素，ASON应抽象为赋权图，因此本文主要研究赋权图的边扩充问题.

2　电力通信ASON模型及其健壮性

2.1ASON数学模型

本节利用图论理论建立电力通信ASON模型.鉴于电力通信ASON的双向传输性以及网络中不同路径的传输代价不相等的特点，本文选用无向赋权图描述ASON.在模型中，ASON设备抽象为图G的节点V＝{v1，v2，…，vn}，连接站点设备的光缆链路抽象为图G的边E＝{e1，e2，…，em}，形成赋权连通图G(V，E，wij).图G连接关系可用邻接矩阵A(G)表示，如果节点vi和vj之间存在光缆的直接连接边eij，则邻接矩阵A(G)中对应的元素aij的值为两节点之间连接边的权值wij，否则为零.与传统网络传输相同，ASON中节点之间业务的传输仍然以最短路为基础.对于赋权图中边的权值，本文采用每条边两端节点度之和作为该边的权值.对网络健壮性优化而言，每条边的权值需表述出该边在保证整个网络业务可靠传输的重要程度，而网络中通常采用链路长度、实际光纤传输衰耗等作为权值的方法仅表征了实际链路传输代价，不能表征该条链路在网络中的重要程度. 网络中，节点的度是经过该节的链路数量，表征了该节点在ASON业务配送时的重要程度.用两端节点的度之和表示与该链路连接的链路数量，可以有效表征该链路传输ASON业务的多少，也就有效表征了该链路在网络健壮性分析中的重要程度.

2.2网络健壮性评价测度

传统图论中评价简单图静态连通性的参数有点连通度κ(v)和边连通度κ(e)，定义为使图G不连通所需删除的最少点或边的数量，但其并不能准确刻画网络通信的健壮性.

如图1所示两拓扑都包含n个节点和n-1条边，图1(a)为链状拓扑结构，图1(b)为星状拓扑结构.由图可知两拓扑的点连通度和边连通度κ(v)＝κ(e)＝1.但两网络在数据传输层面的健壮性存在明显差异：设网络中任意两节点之间均存在通信需求，则当任意一链路断裂时，图1(a)网络受影响通信为n1n2项，其中n1、n2为两连通子图的节点个数，n1＋n2＝n；而图1(b)网络中仅有n-1项业务被中断.通常n1n2n-1，因此图1(b)网络结构具有更高的健壮性.

图1　2种典型拓扑结构Fig.1 Two kinds of typical topology

Fiedler[13]提出一种新的连通度概念——代数连通度，表示动态网络稳定性和健壮性的测度.图G的代数连通度定义为图G的拉普拉斯矩阵L(G)的第2小特征l2(G)[9].拉普拉斯矩阵定义为L(G)：L(G)＝D(G)-A(G)，其中D(G)、A(G)分别是图G的对角矩阵和邻接矩阵.L(G)的元素lij可以表示为

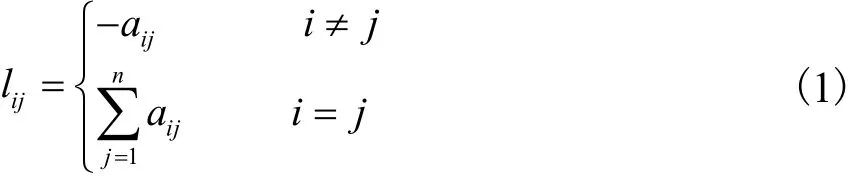
式中aij为图G的邻接矩阵A(G)中的元素.

重新计算图1(a)、(b)的代数连通度，当n＝4时，l2(Ga)＝0.588，l2(Gb)＝1，因此代数连通度可更好地判定网络通信健壮性.鉴于上述分析，本文采用代数连通度作为健壮性边扩充优化的测度.

2.3拓扑优化模型

本文使用代数连通度作为网络拓扑的基本测度，考虑到电力通信ASON光网络的业务传输偏好性，将所研究的问题数学建模表述为：对给定的赋权图G＝(V，E，wij)，如何增加r条边，使得新图的代数连通l2(G′)最大，即最大化加强网络的健壮性.用Er表示增加的r条边，Ecand和Ebase分别表示增边候选边扩充集和原图边集，该模型的数学表达式为

拓扑优化模型关键环节是最优代数连通度的求解，代数连通度的计算过程可以简要地概括为：①计算图G的邻接矩阵A(G)和对角矩阵D(G)；②计算图的拉普拉斯矩阵L(G)＝D(G)－A(G)；③计算拉普拉斯矩阵L(G)的特征值l；④代数连通度即为拉普拉斯矩阵L(G)的第2小特征l2(G).

若将边扩充候选集中每条边依次加入原图计算代数连通度，则计算成本较高.利用以代数连通度为变量的特征方程式在闭区间内的单调有界性，本文将所研究的边扩充优化问题化简为求解单调非线性方程根的问题，提出了赋权网络二分算法以快速求解.

3　网络边扩充优化二分算法

3.1二分算法求解优化模型

前面已经阐述了代数连通度能够更准确地区分网络通信健壮性，对无权图G，文献[14]还证明了其具有良好的区间有界性.

性质1 (代数连通度区间有界性)对于连通图G1＝(V，E1)和连通图G2＝(V，E2)，若E1E2，则有2(G1)(G2).即增加边后新图G′的代数连通度增加且新图G′的代数连通l2(G′)一定在l2(G)，(G)]之间l2(G)l3(G)为原图G的拉普拉斯矩阵的第2小和第3小特征值.

但由分析可知，当考虑电力通信传输业务的偏好性，ASON具有赋权图特征.本文针对非负赋权图，首先证明了其具备单调性，并基于该结论，提出网络边扩充优化二分算法.

文献[15]给出n个节点的赋权图G的拉普拉斯矩阵的特征方程式为

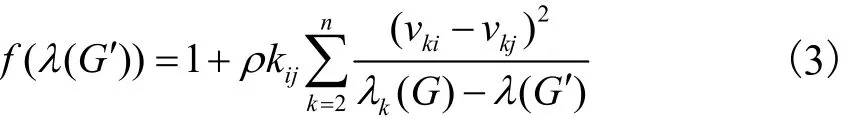
式中：ρ＝1表示在图中扩充边eij，ρ＝－1表示在图中删除边eij；kij为对应修改边eij的权值lk(G)为图G的拉普拉斯矩阵L(G′)的第k个特征值；vki和vkj为第k小特征lk(G)对应的特征向量vk中的第i和第j个元素l2(G′)为图G加边eij后新图G′的拉普拉斯矩阵L(G′)的所有特征值.

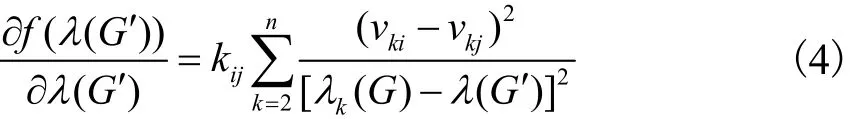
在实际电力通信ASON模型中，所有链路传输代价非负，即图G的边权值kij为非负.在式(4)中，求和部分的分子、分母均为平方项，且(n－1)项分子不可能同时等于零.因此，f((G′))对(G′)的导数值大于零.即赋权图G加边后得到新图的特征方程式f((G′))是在区间l2(G)l3(G)]上以(G′)为变量的单调递增函数.

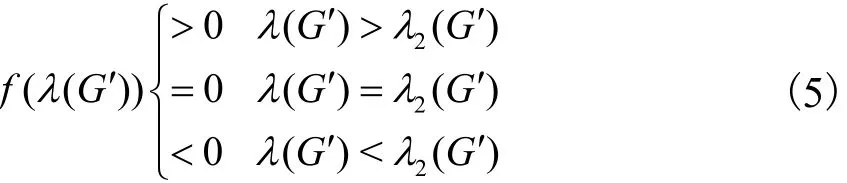
从式(5)可以得到二分算法进行拓扑边扩充实现代数连通度最大化的基本思想：选定初值(G′)，多次循环不断更新(G′)和它的取值上下限及其候选边扩充集St，当St中只含一个元素或(G′)的取值上下限小于某一精度时，结束循环，此时(G′)为最优代数连通度.对于每次循环，首先根据上次循环更新的(G′)，判定候选边扩充集中的所有元素依次向原图中添加边eij后f((G′))的极性.若f(G′))＞0，扩充边eij得到新图的代数连通度在l2(G)l3(G)]之间，则边eij归类到S＋集合；若f((G′))＜0，扩充边eij得到新图的代数连通度l2(G)l3(G)]之间，则将该边归类到S－.根据S＋和S－的情况，剔除候选集中不可能使代数连通度最大化的边，缩小候选集合St，同时更新变量(G′)的取值上下限，重新选定(G′)，进行下一次循环.

赋权图边扩充二分算法如下.

步骤1 输入.原图G的邻接矩阵A(G)、G的拉普拉斯矩阵L(G)以及L(G)的特征l2(G′)和3(G′)；候选集Ecand.

步骤3 循环.第t(t≥1)次循环

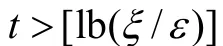
(3) 对St中每个元素进行二分运算：

(4) 更新候选集和区间上下限：

(5) M=(L+ U)/2；

(6) t＝t＋1，并跳转至(1).

步骤4 输出.最优加边的结果eij＝St；加边后新图的代数连通l2(G¢ )=M .

3.2二分算法计算复杂度分析

二分算法的本质可以描述为随着循环次数t的增加，St中元素数量逐渐减小，直至代数连通度的取值上下限|U-L|＜，循环结束.因此算法需要经过[lb(/)]+ 1次循环后输出结果.每次循环前的代数连通度取值上下限满足

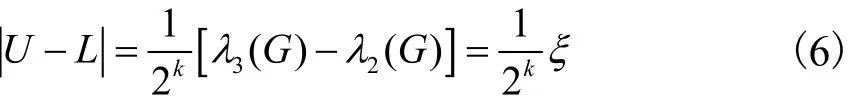
边扩充优化中最优代数连通度选取常用穷枚举法，可表述为：候选扩边集中的边依次加入原图求其代数连通度，进行代数连通度最大化筛选.二分算法的迭代计算在每次循环过程中，同样需要对候选集中每个元素进行操作，看似其复杂度类似穷举法，但实际上却大大降低了复杂度.穷举法在矩阵操作过程中，添加任意一条边都需要修改邻接矩阵A(G)、度对角矩阵D(G)、拉普拉斯矩阵L(G)以及L(G)的特征值等过程.若候选边中有m个元素，则整个穷举法则需要3m次矩阵的修改计算，经过m次特征值的求解.而在二分算法矩阵操作中，仅仅需要计算原图G的邻接矩阵A(G)、对角矩阵D(G)、拉普拉斯矩阵L(G)以及L(G)的特征值和特征向量v.因此，对于候选集中有m个元素时，二分算法的矩阵运算则只需要一次矩阵的计算以及一次特征值和特征向量v的求解，将这一次计算得到的结果作为二分算法的初始化输入.穷举法需要经过重复的矩阵计算，其复杂度为；而二分算法则仅仅需要一次矩阵计算，每条边的计算则是计算各边对应的特征方程式的值，其复杂度为.由于矩阵计算仅需1次，复杂度为，数值相对于循环过程运算复杂度较小.因此，二分算法的计算复杂度为O(4 mnlb(/))，比穷举法降低了O(n2)倍.

4　算法仿真和性能评价

图2　G1～G4网络拓扑Fig.2 Topology of network G1—G4

电力通信ASON是承载配电系统核心交换业务的骨干网络.网络部署遵循电力生产需求，受到电力生产需求，所形成网络具有高连通度特性.对实际电力ASON拓扑分析，平均节点度d(G )Î [3,5].为验证本文提出二分算法的有效性和可行性，仿真依循实际电力ASON拓扑特性，依次生成4种规模的电力ASON.即G1网络：40个节点，86条边，候选边集为694条边；G2网络∶60个节点，128条边，候选边集为1,642条边；G3网络∶80节点，256条边，候选边集为2,904条；G4网络∶160节点，731条边，候选边集为11,989条边.各拓扑连接关系如图2所示.

对上述不同规模网络采用本文提出的网络边扩充二分算法(BA)进行优化，并与GPH(greedy perturbation heuristic)算法[10]、随机边扩充(RE)、弱-弱边扩充(W-W)[8]、强-强边扩充(S-S)和强-弱边扩充算法(S-W)进行优化性能对比.

4.1性能评价指标

在电力通信网络中，多以链路光衰或跳接点为光路选择量度，则端到端路径总长度可与传输延迟相映射，由此仿真中选用路径总长度La作为边扩充网络拓扑承载通信业务能力的评价量度.La定义为网络中所有节点对(i，j)间最短路径和，即为

但当网络由于故障而解列为不连通图时，路径总长度La＝∞，存在局限性.为衡量网络在链路失效时的失健壮性，计算网络效能函数为

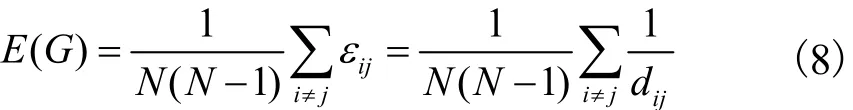
式中εij为节点vi与vj之间的通信效率，εij＝1/dij，当节点vi与vj无可达路径时，dij＝∞，εij＝0，0≤E(G)≤1，因此效能函数E(G)的值越高，网络的健壮性越强.

4.2ASON边扩充优化分析

图3给出不同算法对G1～G4网络进行1边扩充后网络代数连通度.可以看出，较之其他边扩充方法，本文方法和GPH方法的优化效果使网络的代数连通度提升显著.在G2和G3网络中，本文提出的边扩充方法比GPH方法优化后的代数连通度高，这是因为本文算法找到的是最优代数连通度的精确解，而GPH使用贪婪算法，存在局部最优解的干扰.

对优化后的ASON G1～G4网络分析其在链路失效时的健壮性，比较各种边扩充方法的性能，选用网络总路径和效能函数作为评价指标，以介数之和作为链路失效的选择依据，结果见图4和图5.

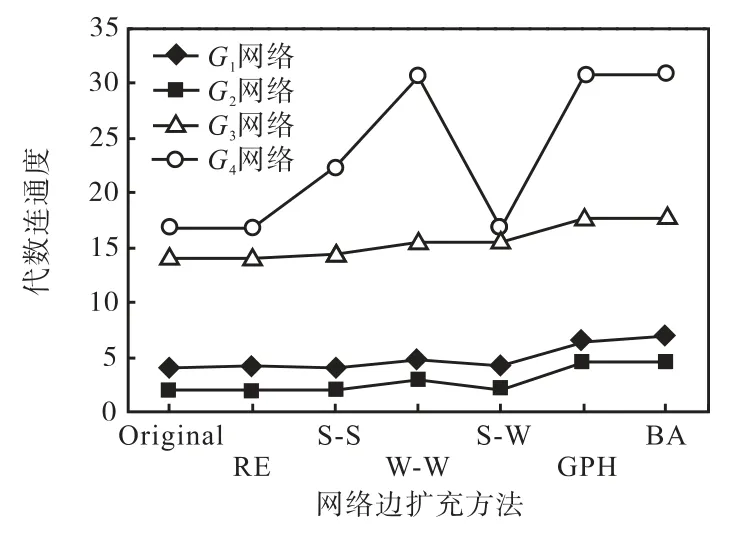
图3　G1～G4网络优化后的代数连通度Fig.3 Algebraic connectivity of optimized network G1—G4

图4　链路失效时网络总路径距离比较Fig.4 Comparison of total length of network path when links fail

边扩充后的网络在链路失效情况下，效能函数增加而网络总路降低，即网络的健壮性提升.本文提出的二分方法和GPH方法均是以代数连通度为测度的，可见本文选用代数连通度测度明显优于其他方法，代数连通度测度方法的网络总路径和效能函数均优于其他方法50%左右.在非代数连通度为测度的4种加边方案中，强-弱和弱-弱策略对健壮性的提升较好.当节点数目较多时，强-弱策略的优化效果优于弱-弱策略；而当网络规模较小时，弱-弱策略的效果较好.

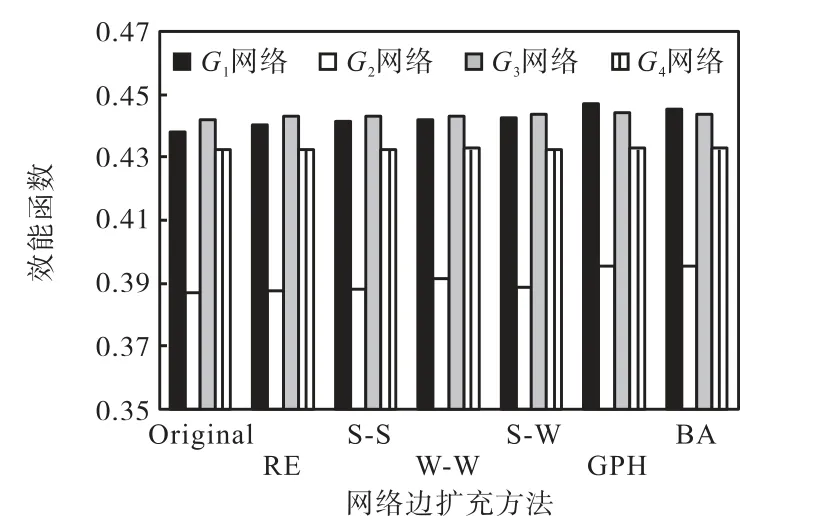
图5　网络效能函数比较Fig.5 Comparison of network’s efficiency function

G1～G4网络优化分析表明本文提出的算法可以精确找到最优代数连通度，提升网络健壮性.此外，还分析了某城区真实配电系统电力通信ASON G网络：8个节点，16条边，候选边集为12条边，其网络拓扑结构如图6所示.依据实际需求，对该网络进行r＝2的边扩充计算.其代数连通度为增加1条边时E(G′)＝20.18和增加2条边的E(G′)＝26.51，均为所有候选集12条边中最优解.因此，边扩充二分算法具有准确寻优且低复杂度的优势.

图6　某城区电力通信ASON G网络Fig.6 Power communication ASON network G

5　结 语

为实现可再生能源高效利用，提升电能供给质量，智能电网需要更准确的电气量测和控制信息.健壮的电力通信网络成为承载复杂信息流的重要底层构建.先进的ASON技术具有动态交换和光网络自动恢复功能，已成为下一代电力通信核心支撑网络.本文利用图论对ASON边扩充优化问题进行建模，采用代数连通度作为边扩充的测度，使用二分方法实现最优代数连通度候选边的选取，设计出一种用于加权网络的边扩充优化二分算法，并分析了算法的计算复杂度.在仿真实验中，依循实际电力ASON拓扑特性，对5种规模网络进行边扩充，并与已有GPH算法等进行比较.结果表明，以代数连通度为测度的加边策略比其他策略加边优化在链路失效情况下，其效能函数和网络总路径的性能提升50%左右.

参考文献：

［1］ Ebenhag S C，Hedekvist P O，Jarlemark P，et al. Measurements and error sources in time transfer using asynchronous fiber network[J]. IEEE Transactions on Instrumentation and Measurement，2010，59(7)：1918-1924.

［2］ 王成山，聂 耸，徐瑞林，等. 分布式电源接入对配电网络重构影响分析[J]. 天津大学学报：自然科学与工程技术版，2014，47(3)：189-194. Wang Chengshan，Nei Song，Xu Rulin，et al. Analysis on the impact of DG on distribution network reconfiguration[J]. Journal of Tianjin University：Science and Technology，2014，47(3)：189-194(in Chinese).

［3］ Ong L Y，Roch E，Shew S，et al. New technologies and directions for the optical control plane[J]. Journal of Lightwave Technology，2012，30(4)：537-546.

［4］ 杨 挺，张倩倩，阎彦含，等. 物联网无线通信传输层动态通道保障机制[J]. 天津大学学报，2012，45(9)：779-784. Yang Ting，Zhang Qianqian，Yan Yanhan，et al. Dynamic transmission channel guarantee mechanism in wireless internet of things[J]. Journal of Tianjin University，2012，45(9)：779-784(in Chinese).

［5］ 常 宁. 国家电网公司 “十一五” 通信规划发展综述[J]. 电力系统通信，2006，27(168)：4-6，16. Chang Ning. Summarization on the 11th five-year telecommunication plan of state grid corporation of China[J]. Telecommunication for Electric Power System，2006，27(168)：4-6，16(in Chinese).

［6］ Ma J，Zhang L，Zhang S，et al. Vulnerability analysis of the optical network NMS[C]//2012 Second International Conference on Instrumentation，Measurement，Computer，Communication and Control(IMCCC). Harbin，China，2012：1185-1187.

［7］ Albert R，Jeong H，Barabási A L. Error and attack tolerance of complex networks [J]. Nature，2000，406(6794)：378-382.

［8］ Beygelzimer A，Grinstein G，Linsker R，et al. Improving network robustness by edge modification [J]. Physica A：Statistical Mechanics and Its Applications，2005，357(3)：593-612.

［9］ Kim Y，Mesbahi M. On maximizing the second smallest eigenvalue of a state-dependent graph Laplacian [J]. IEEE Transactions on Automatic Control，2006，51(1)：116-120.

［10］ Ghosh A，Boyd S. Growing well-connected graphs [C]//45th IEEE Conference on Decision and Control. San Diego，USA，2006：6605-6611.

［11］ Ibrahim A S，Seddik K G，Liu K J R. Improving connectivity via relays deployment in wireless sensor networks[C]//Global Communications Conference. Washington，DC，USA，2007：1159-1163.

［12］ Kim Y. Bisection algorithm of increasing algebraic connectivity by adding an edge[J]. IEEE Transactions on Automatic Control，2010，55(1)：170-174.

［13］ Fiedler M. Algebraic connectivity of graphs[J]. Czechoslovak Mathematical Journal，1973，23(2)：298-305.

［14］ Boyd S. Convex optimization of graph Laplacian eigenvalues[C]//Proceedings on the International Congress of Mathematicians. Madrid，Spain，2006：1311-1320.

［15］ Kim Y，Zhu G，Hu J. Optimizing formation rigidity under connectivity constraints [C]//49,th IEEE Conference on Decision and Control. Atlanta，USA，2010：6590-6595.

(责任编辑：孙立华)

Bisection Algorithm of Edge Augmentation for Electrical Power Communication Network

Yang Ting1，Yuan Bo1，Zhao Chengli2，Wu Cheng1，Pen Haibo1
(1. School of Electrical Engineering and Automation，Tianjin University，Tianjin 300072，China；2. Tianjin Navigation Instruments Research Institute，Tianjin 300131，China)

Abstract：With the development of smart grid，the structure of electrical power communication automatic switched optical network(ASON) is getting increasingly complex. Topology optimization becomes one of the key technologies to guarantee the transmitting reliability as well as improve the robustness of network. In this paper，ASON’s topology optimization problem was modeled and a bisection algorithm of edge augmentation for weighted network was proposed，in which the algebraic connectivity was defined as counting measure. The monotonicity of the characteristic equation corresponding to Laplace matrix for weighted graph was theoretically proved. Therefore，the bisection algorithm was employed to rapidly solve this monotone nonlinear characteristic equation and the optimal edge-expansion strategy was obtained. Simulation results show that when links fail，the bisection algorithm of edge augmentation can present exact solutions with low complexity of O(4mn lb(x/d))，which can effectively reduce point-to-point communication path length and also improve the value of network’s efficiency function.

Keywords：electrical power communication network；edge augmentation；bisection algorithm；network efficiency function

通讯作者：杨 挺，yangting@tju.edu.cn.

作者简介：杨 挺（1979— ），男，博士，教授.

基金项目：国家国际科技合作专项资助项目(2013DFA11040)；国家自然科学基金资助项目(61172014)；天津市自然科学基金资助项目(12JCZDJC21300).

收稿日期：2014-03-15；修回日期：2014-03-18.

DOI:10.11784/tdxbz201401040

中图分类号：TM73；TP393

文献标志码：A

文章编号：0493-2137(2015)06-0481-07