基于聚类分析法的公共自行车服务系统研究

周素静，徐宝林，刘冬华，郭文秀

(郑州铁路职业技术学院，河南 郑州 450052)

0 引言

本文的案例来源于2013 年全国大学生数学建模竞赛的D 题。

公共自行车作为一种环保、节能、健康的出行方式，正在全国许多城市推广与普及。在公共自行车服务系统中，自行车租赁站点的位置及锁桩和自行车数量的配置，对系统的运行效率与用户的满意度有重要的影响。

题目附件1［6］为浙江省温州市鹿城区公共自行车管理中心提供的某20 天借车和还车的原始数据，所给站点的地理位置参见附件2［6］。在搞清楚公共自行车服务模式和使用规则的基础上，根据附件提供的数据，建立数学模型，讨论以下问题:

(1)找出合计用车次数最大的一天;定义两站点间的距离并计算已知站点中每两站点间的距离。

(2)统计用车次数最多的一天各站点的借车高峰时段和还车高峰时段，在地图上标注或列表给出高峰时段各站点的借车频次和还车频次，并对具有共同借车高峰时段和还车高峰时段的站点分别进行归类。

根据公共自行车服务模式和使用规则以及温州市鹿城区公共自行车服务指南，结合实际情况，作出如下假设:

(1)附件1［6］中的数据能够反映该城区公共自行车服务系统的现状;

(2)附件1［6］中借出车站号和还车车站号相同，且用车时长小于等于1 分钟的记录为无效记录，建立模型时不予考虑;

(3)附件1［6］中还车车站号为0 的记录，认为该车丢失或损坏，统计借车频次时有效，而统计还车频次时无效;

(4)每次用车时长不超过24 小时(即1440 分钟)的数据为有效数据;

(5)各站点所提供的自行车型号相同，且每位用车人的车速基本相同，为12km/h。

根据以上假设，首先对附件1［6］中借车和还车的原始数据进行预处理，把借出车站号与还车车站号相同且用时小于等于1 分钟的记录以及每次用车时长超过24 小时的记录删除，得到20 天数据的预处理表。

对于问题(1)，找出用车次数最大的一天，定义两站点间的距离，并以该天的数据计算出已知站点中每两点间的距离，根据计算的结果分析目前该区站点的设置是否合理。

对于问题(2)，利用spss 统计出用车次数最多的一天各站点的借车最高时段和还车高峰时段及频次，并对具有共同借车高峰时段和还车高峰时的站点分别根据借、还车频次进行聚类分析。然后利用聚类分析的结果评价各站点的自行车数量和锁桩数配置是否合理，并给出高峰时段站点间自行车的调配方案。

1 两站点距离模型的建立与求解

(1)数据的预处理

由假设2 和假设4 可知，每次用车时长超过24小时，以及借出车站号与还车车站号相同且用车时长小于等于1 分钟的为无效租车记录，所以要对附件1［6］中借车和还车的原始数据进行预处理。将20 天的数据表导入软件spss，利用数据筛选功能，删除上述两类记录，得到20 天借车与还车数据的预处理表，并将它们导入spss，建立spss 数据文件。

由数据表统计可知:20 天中每次用车时长不超过30 分钟的占98%;第13 天的合计使用公共自行车次数最多，为38800 次。

(2)计算两站点之间的距离，并求出最长距离和最短距离

由于实际城市交通中两站点间有不同的路线，为了更好地与实际交通情形一致，两站点的距离可以用一定时段内(比如一周或有代表性的一天)两站点间的平均用车时长与车速的乘积来计算。记自行车的平均车速为v;第13 天两站点间所有有效借车记录中的用车时长的平均值为¯t;两站点间的距离记为d;两不同站点之间所有有效借车记录中的用车时长分别为t1，t2，…，tm，则有

其中，v 根据假设5 取为12m/h。

利用第13 天借车、还车数据，按定义(1)，利用matlab 编程求任意两不同站点之间的距离及平均距离，得到平均距离为3.5349km，各站点间的距离如表1 所示。

表1 不同站点间的距离 (单位:km)

从表1 可以看出，站点号为123 的杏花路十七中路口与站点号为5 的星河广场之间的距离最长，为74.8km;最短距离为0.2km，对应的站点号有两对，分别为98 的市公安局与106 的金桥路桃源、34的广信大厦与174 的信河嘉会里路口站。

根据国内外调查研究，出行距离为200～300m时，人们通常会选择步行方式;出行距离为0.5～5.5km时人们会选择公共自行车方式。所以为了方便市民出行和提高公共自车服务系统的效率，两公共自行车站点的距离以0.3～5.5km 比较合理。由前面的计算可知，温州市鹿城区公共自行车服务系统中所有站点间的平均距离为3.5349km，在合理距离范围内，这说明该系统站点的设置是基本合理的。对于距离较大的站点，可再结合附件2 所给站点的地理位置及周边自行车站点的具体情况，适当增加一些站点。例如，站点号为118 的上陡门住宅公交站和站点号为149 的均瑶宾馆对面的距离为20.2km，且中间站点比较少，可以在这两点间合适的位置增加新站。

2 借车与还车高峰时段分析模型的建立与求解

首先，将第13 天数据表中的借车时刻和还车时刻进行整点处理(例如，17:00:00-17:59:59 转换成17 点，按17-18 时段统计)，然后利用spss 的交叉列联表功能对第13 天各个站点借车和还车的时段进行统计分析，得到各站点的借车高峰时段和还车高峰时段，及相应时段的借、还车频次(如表2 所示)。

表2 各站点的借车和还车高峰时段及相应的借车频次和还车频次(按各站点借车高峰时段的借车频次排序)

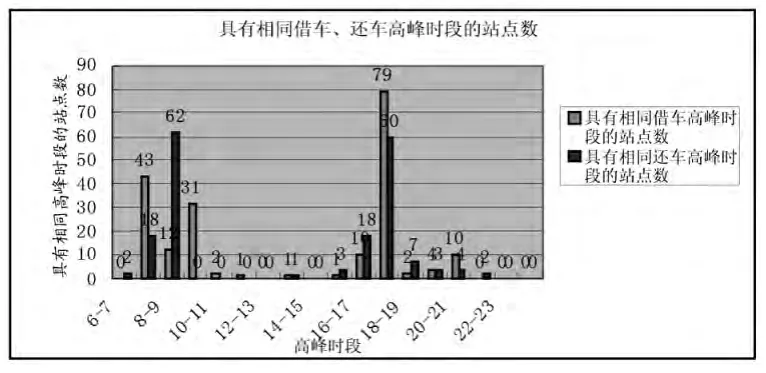
图1 具有相同借车、还车高峰时段的站点数

对表2 进一步分析，统计出各借车高峰时段和还车高峰时段的站点数，如图1 所示。可以看出借车高峰时段在7-8、17-18 和9-10 时段的车站较多;还车高峰时段在8-9 和17-18 时段的车站较多。将各站点借、还车高峰时段的借车频次和还车频次标注在该区的交通图上，如图2 所示。将这些数据和图上传到网上，可以方便市民出行时选择合适的路线，避开高峰站点，及时租到自行车。另外，从借车高峰时段的借车频次来看，街心公园和五马美食林的借车频次分别为154 次和119 次，远远大于该站自行车的锁桩数40 个，即使按每次用车时长不超过30 分钟，仍然不能满足需求，需要增加自行车和锁桩数或者在高峰时段从相邻的用车频次较低的车站调运车辆;用车频次在50～70 次的站点(如开太百货等)，高峰时段的用车频次与配备的自行车和锁桩数基本相符，说明这些站的设施基本满足需求。

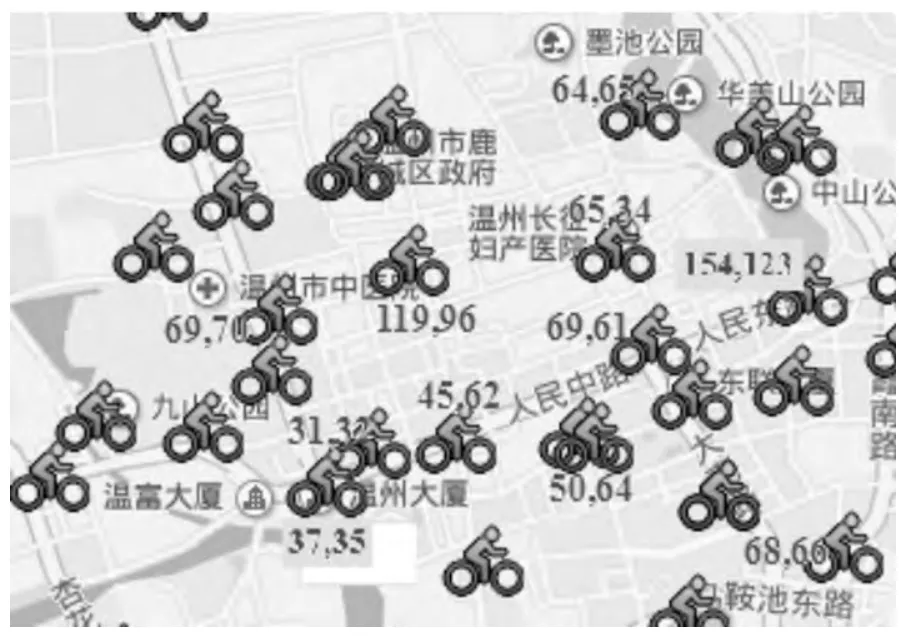
图2 各站点借、还高峰时段的借车频次和还车频次

3 具有相同借车高峰时段、还车高峰时段的站点的聚类分析模型

为了研究各站点的自行车数量和锁桩数等设施设置是否合理，以及如何在高峰时段合理调度自行车，下面用聚类分析法对几个主要借车高峰时段和还车高峰时段的站点进行聚类分析。

设具有相同借车(或还车)高峰时段的站点数为n，利用spss 的交叉列联表分析功能，统计出借车高峰时段在该站点的借车频次和还车频次，分别记为xi，yi(i=1，2，…，n)，则两站点的欧式距离为:

定义两站点的“亲疏程度”用它们的欧式距离表示。

(1)借车高峰时段为7-8 时的站点的聚类分析

利用spss 统计出7-8 时借车高峰时段的43 个站点的借车频次和还车频次，利用K-Means 聚类分析法得到的聚类分析结果如表3 所示。

表3 借车高峰时段为7-8 时的站点的聚类分析结果

从表3 可以看出，这一时段类型1 和类型2 的借车频次均不超过40，如果每次用车时长按30 分钟计，这两类中的站点配置20 辆自行车和30 个锁桩即可基本满足需要，对照目前的锁桩数，可以看出这些站点目前的设施基本满足需求;类型1 中的站点借车频次明显高于还车频次，容易造成无车可借的情形，实际运行中可以适当从其它站点调运车辆以满足这一时段的需求;类型3 中借、还车频次均不超过20，说明这些站点不是用车繁忙的站点，配置10辆自行车和锁桩数基本可以满足需要，而目前这些站点的锁桩数均不小于20，因此这些站点的设施即使是在高峰期也是富余的，在这一时段可将多余的车辆调往附近用车量大的站点。

(2)借车高峰时段为17-18 时的站点的聚类分析

利用spss 统计出17-18 时借车高峰时段的78个站点的借车频次和还车频次，利用K-Means 聚类分析得到的结果如表4 所示。

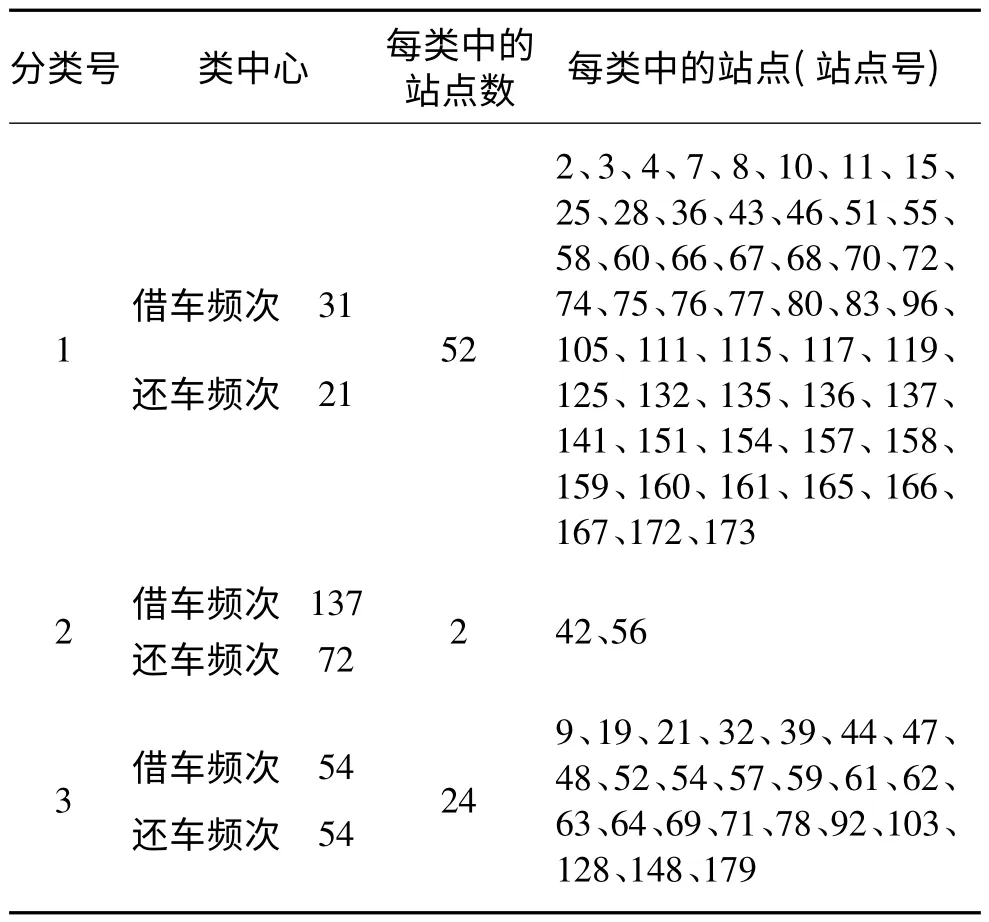
表4 借车高峰时段为17-18 时的站点的聚类分析结果

从表4 可以看出，类型3 中的站点借车频次和还车频次基本相同，借车和还车的频次均不超过60，如果每次用车时长按30 分钟计，这些站点合理的自行车数量和锁桩数应为30，对照目前的设施大部分站点的锁桩数为30 或40，基本满足要求，对于一些锁桩数为20 的站点，需要适当增加一些车辆和锁桩数或将附近站点的车辆调度到这些站来满足这一时段的需求;类型2 中的站点借车频次远远高于还车频次，且用车频次均高于70，即使每次用车时长按30 分钟计，合理的自行车数量和锁桩数应不少于40，这一数值高于绝大部分站点目前的设施数，说明目前的设施不能满足要求，需要适当增加一些车辆和锁桩数;类型1 中的站点借车频次略高于还车频次，且均为30 左右，合理的设施配置和目前的基本相同，可以认为这些站点的设施基本能满足要求。

(3)还车高峰时段为8-9 时的站点的聚类分析

利用spss 统计出8-9 时还车高峰时段62 个站点的借车频次和还车频次，利用K-Means 聚类分析得到的结果如表5 所示。

表5 还车高峰时段为8-9 时的站点的聚类分析结果

从表5 可以看出，三个类型在这一时段的还车频次均大于借车频次。类型2 和类型3 中的站点借车频次均不超过40，合理的自行车的数量和锁桩数应为20～30，对比目前这些站点的锁桩数，可以认为这些站点的设施是基本满足用车需要的;类型1 中的站点借车频次虽然高于50，配置自行车的数量应不少于30，且由于还车频次明显高于借车频次，所以这些站点需要适当增加锁桩数以满足这一时段的需求。

(4)还车高峰时段为17-18 时的站点的聚类分析

利用spss 统计出17-18 时还车高峰时段60 个站点的借车频次和还车频次，利用K-Means 聚类分析得到的结果如表6 所示。

表6 还车高峰时段为17-18 时的站点的聚类分析结果

从表6 可以看出，三个类型在这一时段的还车频次均大于借车频次。类型1 中各站点的借车频次均不超过40，合理的自行车数量和锁桩数应为20，对照目前的设施，可以认为这些站点的设施是基本满足用车需要的;类型2 中的站点借车频次和还车频次基本相当，且借车频次高于50，说明这些站点配置30 辆自行车和锁桩数比较合理，所以对于部分锁桩数为20 的站点需要适当增加车辆数和锁桩数来满足这一时段的需求;类型3 中的站点借车频次小于20，说明目前这些站点的设施在这一时段是富余的，可以将车辆调到临近用车紧张的站点去。

［1］韩中庚.数学建模实用教程［M］.北京:高等教育出版社，2012.

［2］薛薇.SPSS 统计分析方法及应用(第二版)［M］.北京:电子工业出版社，2009.

［3］李黎辉，陈华，孙小丽.武汉公共自行车租赁点布局规划［J］.城市交通，2009(7):39-44.

［4］姚遥，周杨军.杭州市公共自行车系统规划［J］.城市交通，2009(7):30-38.