对比，在认知冲突中引入新知——以人教版七年级上册“1.2.2数轴”为例

☉江苏省如皋市搬经镇高明学校 孙瑜华

对比，在认知冲突中引入新知
——以人教版七年级上册“1.2.2数轴”为例

☉江苏省如皋市搬经镇高明学校 孙瑜华

数轴，是初中数学的一个重要概念，是学生学习有理数的运算、平面直角坐标系的基础.人教版教材将数轴安排在七年级上册第一章有理数之中，这节内容的学习将使学生第一次接触到数形结合思想，体会其在数学问题解决中的价值.因此，我们要高度重视从实际情境中抽象出数轴的过程的设计，创造出利于认知冲突生成的情境，让学生体会到数轴出现的必要性和适时性.

一、“1.2.2数轴”教学片断

问题：在一条东西向的马路上，有一个汽车站牌，汽车站牌东3m和7.5m处分别有一棵柳树和一棵杨树，汽车站牌西3m和4.8m处分别有一棵槐树和一根电线杆，试画图表示这一情境.

教师呈现上面的“问题”后，要求学生自己尝试“画图表示这一情境”.在此过程中，教师在学生中间走动，巡视其作图状况.6分钟后，学生完成作图，教师将“问题”撤去，将学生画出的图1—图4同时投影展示.

图1

图2

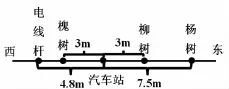
图3

图4

接下来，请学生在小组中交流各幅图是如何“描述”问题情境的，还有什么不足的地方，怎么“补救”.根据老师的要求，各小组进行了5分钟热烈的交流，每一名同学都积极地发表自己的见解.在最后的全班交流中，教师让学生面向全班交流组内互动的成果.每一个小组均派出代表，对本组探讨的成果进行了充分展示.有小组认为，四幅图都都清晰地呈现出了“问题”中的汽车站、柳树、杨树、槐树和电线杆的位置，但图1、2中不能一下子就读出它们之间的距离，在这一点上，图3、4是优于前两幅图的.有小组认为，图3和图4不仅能看出位置关系，还按比例给出了“问题”中的距离，让人一目了然，但两者相比，图4的简洁程度是优于图3的.还有小组提出，图4中标注的“3m”、“4.8m”和“7.5m”都是与汽车站的距离，在标注了“东”和“西”之后，数字的意义才明晰了，根据前面刚刚学习的正负数的意义，可以用正负数来表示“东、西”这对相反意义的量.

最后，教师进行了总结：对比这四幅图，我们不难发现，想要清晰而又简洁地向别人描述“问题”情境，我们可以在一条直线上选择一个分界点表示汽车站，并将向右的方向规定为正方向（在图4中投影“箭头”，如图5，下同），在这个分界点的两侧分别用正、负数来表示柳树、杨树、槐树和电线杆的位置和它们与分界点间的距离（在描述过程中，先投影“0”表示出汽车站，然后分别将图4中的两个“3m”、“4.8m”和“7.5m”隐去，并用“-3”、“3”、“7.5”和“-4.8”投影替代）.这就是我们今天要学习的数轴.（板书课题）

图5

二、片断简析

让学生直接作图描述“问题”情境，不仅要唤醒学生数形结合的意识，还要梳理前学段学过的比例尺、方位、距离等知识.图1至图4都是教师预料之中的成果，通过学生解答时的巡视，最终教师将这四种图形同时投影展示，“有对比才有鉴别”，学生面对差异明显的图形，自然会有所感悟.在探究与交流中，主动生成的“如何才能更好地描述‘问题’情境”，自然成为了小组交流和个体思考的重要话题，对这一话题的不断深入的探讨，会让数轴的引入变得越来越顺利.当然，在现有认知水平下，想要让学生自己说出数轴的作法并给出图5，是不太可能的.所以教师用学生之间的交流和面向全班的交流，让学生脑海中原本含糊的“分界点”“方向”“距离”等变得清晰了.最后的总结，就是“锦上添花”，梳理了学生交流的成果，顺利地引出了数轴，是一举两得的好事.

三、几点感悟

1.对比是制造认知冲突的有效手法

对比是“一种行之有效的教学手法”，对比资源的呈现，激活了学生辨明“是非”的欲望.由不同的资源间的差异所引发的思辨，让学生的认知产生了激烈的冲突.思维的碰撞，梳理了知识，激活了技能，为新的知识的出现奠定了坚实的基础.数轴是学生进入初中后的第一次数与形的结合，这对学生的后续学习十分重要.为了引导学生顺利获得这一知识，教师将学生作出的四个不同层次的图形同时投影展示，形成了较为强烈的对比，图1中的点“有序”但“距离无差别”，对情境的“描述”显然是不到位的；图2中看似距离有了区分，但问题情境的“撤离”，学生是看不出具体的数值的；图3和图4有了很大进步，但两者又各有不足，图3的“描述”略显烦琐，图4较为简洁，但文本的参与度还较高，尤其是两个“3m”陈述并不容易.自此，认知冲突形成.接下来的教学，我们应让学生充分解读给出的这四幅图，让他们在对比与辨析中努力实现认知的平衡，扫清新知出现的“障碍”.

2.多维交流让对比教学成效凸显

“话越说越清，理越辩越明”.在形成激烈认知冲突后，教师设计的小组交流与全班交流活动，会让学生的思维产生碰撞，从而生成符合教学需求的交流成果.由于个体认知的差异，无论是组内交流，还是全班交流，都可能会出现众多的交流成果.在对比教学中，教师展示的差异明显的资源会让学生的交流成果多样化、具体化.本文中基于图1至图4组内和全班的“双重”交流，让每一名学生都有了阐述自己对图形的理解的机会.通过不同维度的交流，学生在图形的反复解读中，明晰了图形间的差异、各个图形“描述”的不足及相应的“补救”措施.这些都是学习数轴的基础，一直潜藏在学生的知识网络中，有的放矢的多维交流既起到了唤醒旧知的作用，又实现了梳理铺垫的作用，对比教学的价值被凸显无遗.

3.新知引入要顺应学生的认知规律

任何一个新知识的出现都非“无源之水”，在教学中我们都应理清其来龙去脉，让新知教学在符合学生认知规律的状况下有序推进.可见，新知的引入应是对学生既有基础的一种顺应，是一种知识、能力的自然延续，而不是为了教学而教学的强行“切入”.以数轴的学习为例，这是对前学段线段图的更进一步认知，是比例尺、线段图和正负数的一次有效融合.因此，数轴教学就应从梳理学生的这些知识基础入手.用好教材给出的“问题”，让学生自主作图，并进行多维交流.很显然，本文案例中的学生活动带来了丰硕的成果，学生对作出的图形的辨识交流，让数轴的建构基础得以清晰呈现，而这些知识间能够相互附着的“生长点”也在交流中得以全盘出现.应该说，这样的教学历程，顺应了学生的认识需求，完全符合循序渐进获取数学知识、形成数学技能的教学规律.

1.印冬建.对比：一种行之有效的教学手法［J］.中学数学教学参考（中），2014（1）.

2.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

3.陈浩.理清基本经验，为新知探究夯实基础——以“数轴”为例［J］.中学数学（下），2015（4）.Z