基于工况传递路径分析的挖掘机座椅振动研究

庞晓柯， 周以齐， 唐 伟， 王 丽,2， 米永振

(1.山东大学 机械工程学院 高效洁净机械制造教育部重点实验室，济南 250061; 2.齐鲁工业大学 机械与汽车工程学院，济南 250353)

基于工况传递路径分析的挖掘机座椅振动研究

庞晓柯1， 周以齐1， 唐 伟1， 王 丽1,2， 米永振1

(1.山东大学 机械工程学院 高效洁净机械制造教育部重点实验室，济南 250061; 2.齐鲁工业大学 机械与汽车工程学院，济南 250353)

以某挖掘机新产品试验车为对象，研究发动机到驾驶室座椅的振动传递情况。应用奇异值分解技术对工况传递路径分析方法进行了改进，并采集运行工况试验的振动数据，建立了从发动机振动到驾驶室座椅振动的工况传递路径分析模型。对比座椅安装位置加速度的模型合成信号与实测信号的频域特征，研究发现两者吻合较好，从而验证了模型的正确性。对模型合成的输出信号进行频域分析，可以直观的研究需要关心的频率。结合各路径的振动贡献频谱图与矢量图，找出特定频率处需要改进的路径。最后利用传递率函数频谱图和输入加速度频谱图，提出具体的改进方法，为解决振动噪声传递类问题，提供了工程参考。

工况传递路径分析；奇异值分解；振动贡献；传递率函数

挖掘机的振动不仅是影响结构零部件疲劳破坏、机器使用寿命的主要原因，也是影响操作人员使用舒适性重要因素。为了研究和改善某挖掘机新产品座椅的振动问题，本文对该产品样车座椅的振动传递路径进行分析。挖掘机座椅的振动是由多个激励源，通过各自不同的路径传递至座椅后叠加而成。传递路径分析(TPA, Transfer Path Analysis)是研究振动噪声传递特性的经典方法[1-3]。通过它可以分析激励通过各自传递路径对目标位置振动噪声的贡献量，并能确认是激励还是系统本身(传递函数)主导了路径贡献，通过控制和改进路径贡献，将目标位置的振动噪声控制在预定的范围之内[4-7]。

传统TPA方法是一种研究振动噪声十分有效的方法，通过它可以获得系统激励、传递函数的详细信息。然而，传统传递路径分析模型的建立，测试过程中需要拆除动力系统，并且需要大量繁琐的频率响应函数测试工作。因此近几年工程师们提出来一种简单快捷的方法：工况传递路径分析(OTPA,Operational Transfer Path Analysis)[8-10]。该方法只需要测试工况下的振动噪声数据，即可建立分析模型，消除了传统传递路径分析方法的缺陷。但是由于测试数据存在一定的信号噪声、系统输入之间存在部分相关性和相互串扰，此时利用OTPA方法可能会出现较大误差[11]。奇异值分解是一种重要的矩阵处理技术，工程上常被用来去除数据中的干扰噪声和相关性，提高数据的有效性[12-14]。Reninger等[15]应用奇异值分解技术，对空气中的时域电磁信号进行处理，去除了电磁信号中的信号噪声。付俊涵[16]应用奇异值分解技术，消除了多声源通道信号之间的相互串扰。

本文应用奇异值分解技术对OTPA方法进行改进，对挖掘机的工况振动测试数据进行处理，研究发动机激励对驾驶室座椅的振动传递。

1 工况传递路径方法原理

在传统TPA方法中，假设系统是线性时不变的，系统的输出是系统的输入沿各自的传递路径传播至输出位置后叠加而成。系统传递特性可以用式(1)表示。

(1)

式中：Yj为系统第j(j≤m)个输出(振动加速度、声压等)；Xi为系统第i(i≤n)个输入(力、加速度、声压等)；Hij为输入Xi到输出Yj的传递函数(振动传递函数、噪声传递函数等)。

将式(1)写成矩阵形式为：

Y=XH

(2)

OTPA方法用工况测试条件下的激励处响应信号代替式(2)中的输入，用传递率函数矩阵代替式(2)中的传递函数矩阵，即：

Y=XT

(3)

T=(XTX)-1(XTY)=G-1xxGxy

(4)

式中：T为传递率函数矩阵(其中的元素Tij表示Xi到Yj的传递率函数)；Gxx为输入变量的自功率谱矩阵；Gxy为输入变量与输出变量的互功率谱矩阵。

由式(4)可知，传递率函数矩阵T是通过工况测试输入输出数据计算得到，避免了拆除动力系统和繁琐的频率响应函数的测量(锤击试验)，极大地减少了测试工作量。但是不可避免的是，测试信号存在一定的信号噪声、路径之间存在一定的相互串扰、输入之间存在部分相关性，此时使用式(4)、(3)描述的OTPA模型计算出的结果可能出现较大误差。

为了克服工况传递路径方法的缺点，本文应用奇异值分解对OTPA方法进行改进。首先对输入变量矩阵进行奇异值分解：

X=U∑VT

(5)

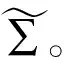
由式(5)和(4)可得路径的传递率矩阵为：

(6)

将式(6)代入式(3)可得OTPA模型的合成输出信号为：

(7)

各路径的传递贡献为：

(8)

2 挖掘机座椅振动分析

2.1 OTPA模型建立与验证

挖掘机座椅的振动来源比较复杂，发动机、传动系统、液压系统、路面不平衡等引起的振动通过各自的传递路径传递到座椅。建立OTPA模型的时需结合实际情况做适当的简化，在定制试验条件(额定转速空载稳态)下，座椅的振动主要来自于发动机的竖直振动，因此本文主要研究发动机的竖直振动对挖掘机座椅的振动传递，以发动机减振后在机架上4个安装位置的竖直方向振动加速度作为输入变量x1,x2,x3,x4，以座椅安装位置的竖直方向振动加速度作为输出变量y，建立OTPA模型，如图1所示。

图1 OTPA模型示意图Fig.1 Schematic of OTPA

为了提高传递率函数的计算准确性，需要确保激励数据不重复，并且工况试验次数大于等于系统输入个数。本文结合实际情况取4个试验工况，分别对应从低到高4个不同转速。详细的试验测试如表1所示，测试现场及测点布置如图2所示。

图2 试验现场及测点布置Fig.2 Test field and acceleration measuring point

表1 OTPA试验方案

依据以上应用奇异值分解技术改进的OTPA理论，对测试得到的数据进行处理。定制试验条件即额定转速2 390 r/min工况下，模型合成的座椅安装位置加速度输出信号，可由式(7)可求得，将模型合成的输出信号与实测的输出信号进行对比，结果如图3所示。

图3 合成的输出信号与实测的输出信号对比Fig.3 Comparison of output signal and synthesized signal

由图3可知，OTPA模型合成输出信号在大部分频段内与实测输出信号近似重合，本文建立的OTPA模型的正确性得到了验证；在个别频率处仍存在一定的误差，这些误差主要是由模型假设和简化造成的，具体包括：① 建立模型的时候主要考虑了发动机的竖直振动激励，忽略了其他激励源，如传动系统振动、液压系统振动等；② 由于测试条件等限制，导致系统输入的测试信号与真实信号有一定误差；③ 真实系统具有一定的非线性。

分析图3可知，路径总传递贡献在20 Hz、80 Hz、221 Hz、441 Hz处的振动幅值比较大，对挖掘机座椅的振动影响显著，需要重点研究。

2.2 OTPA结果分析

2.2.1 路径振动贡献分析

使用上述OTPA模型，由式(8)即可计算出各路径的振动贡献，各路径的振动贡献频谱图如图4所示。

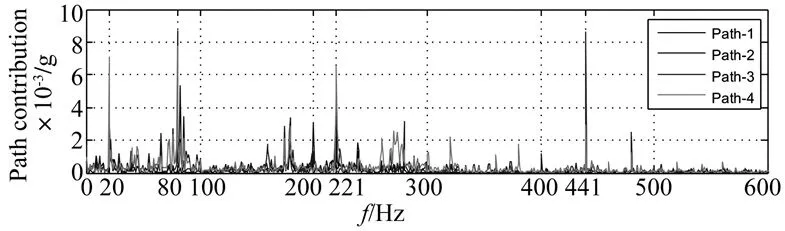
图4 路径振动贡献频谱图Fig.4 Spectrum of path vibration contribution

由图4可知：在20 Hz处，各路径的振动贡献大小为：Path-4>Path-2>Path-1>Path-3；在80 Hz处，各路径的振动贡献大小为：Path-2>Path-4>Path-3>Path-1；在221 Hz处，各条路径上的振动贡献大小排序为：Path-4>Path-1>Path-2>Path-3；在441 Hz处，各路径的振动贡献大小为：Path-3>Path-4>Path-2>Path-1。由于振动的叠加不是简单的相加减，而同时考虑幅值和相位，因此将20 Hz、80 Hz、221 Hz、441 Hz处各路径的振动贡献以矢量图的形式表示，如图5～8所示。

图5 20 Hz振动贡献矢量图Fig.5 Vector of path vibration contribution at 20 Hz

图6 80 Hz振动贡献矢量图Fig.6 Vector of path vibration contribution at 80 Hz

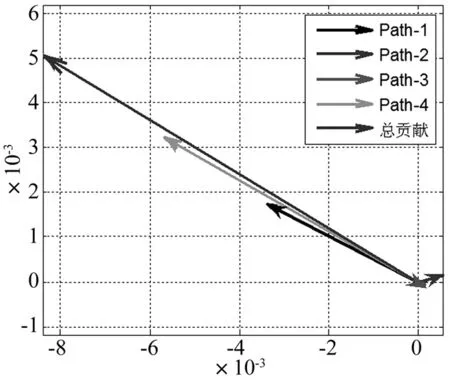
图7 221 Hz振动贡献矢量图Fig.7 Vector of path vibration contribution at 221 Hz

图8 441 Hz振动贡献矢量图Fig.8 Vector of path vibration contribution at 441 Hz

由图5可知，在20 Hz处，各路径振动贡献的相位各不相同，其中Path-4、Path-2的振动贡献与振动总贡献的相位差为锐角，对振动总贡献的叠加效果为正，Path-1、Path-3与振动总贡献的相位差为钝角，对振动总贡献的叠加效果为负。由于Path-4有效振动贡献即在总贡献上的投影明显大于其他三个路径的贡献，因此降低20 Hz振动总贡献的有效方法是降低Path-4即发动机右前振动的传递贡献。

由图6可知，在80 Hz处，各路径振动贡献的相位相同，对振动总贡献的叠加效果为全为正，由于Path-2、Path-4的有效振动贡献明显大于Path-3，Path-1，因此降低80 Hz振动总贡献的有效方法是降低Path-2、Path-4即发动机左前、右前振动的传递贡献。

由图7可知，在221 Hz处，Path-4、Path-1的振动贡献与振动总贡献的相位基本相同，对振动总贡献的叠加效果近似全为正，Path-2的振动贡献与振动总贡献的相位差为钝角，对振动总贡献的叠加效果为负，Path-3的振动贡献近似为零。由于Path-4、Path-1的有效振动贡献远大于Path-2，因此降低221 Hz振动总贡献的有效方法是降低Path-4、Path-1即发动机右前、左后振动的传递贡献。

由图8可知，在441 Hz处，各路径振动贡献的相位相同，对振动总贡献的叠加效果全为正，Path-3、Path-4的有效振动贡献明显大于Path-2，Path-1，因此降低80 Hz振动总贡献的有效的方法是降低Path-3、Path-4即发动机右后、右前振动的传递贡献。

2.2.2 传递率函数与激励输入分析

各输入激励经各自的传递路径传递到目标位置处形成各自的贡献信号，系统的传递率函数T是工况传递路径分析的重要系统动力学参数，它描述了在频域中贡献信号与输入信号的幅值比和相位差。本文的系统振动传递率函数可由式(6)求得，其幅值谱结果如图9所示。各路径加速度激励输入如图10所示。

图9 路径传递率函数Fig.9 Path transmissibility function

图10 系统输入Fig.10 System input

分析图9可知，各路径在300 Hz之前的一些频率处传递率大于1，说明对应频带激励沿着相应路径传递的过程中振动被放大了；300 Hz之后，传递率函数比较小，说明这些频带的加速度激励经过各个路径传递到座椅都有较大的衰减。由图10可知，300 Hz之前除80 Hz之外，各路径的加速度输入激励均较小，反映了此频带的发动机振动激励经减振器减振之后，振动加速度明显被衰减；80 Hz和大于300 Hz的一些频率处的输入加速度较大，可以考虑进一步降低这些频带的振动激励。

在20 Hz附近，各路径的加速度输入激励均比较小，而各路径的传递率函数均大于2.8，振动加速度输入经过各路径传递之后均被放大了，最大Path-4的振动被放大约5.3倍，由此可知该频率很可能是系统的共振频率。此工况下的发动机转速为2 390 r/min，挖掘机的发动机为4冲程柴油发动机，通过计算得到发动机的1/2阶振动频率恰为20 Hz。因此须考虑采取措施使该共振频率避开发动机的1/2阶振动频率。

在80 Hz处，各路径的传递率函数均较小而加速度输入激励均较大。挖掘机的发动机为4缸4冲程，通过计算得到发动机的发火频率恰为80 Hz。说明经减振器减振之后，输入位置在发火频率80 Hz的振动加速度分量仍然较大。由此可知，发动机减振器在发火频率的减振效果仍不理想，因此需要改进发动机在发火频率的减振性能。

在221 Hz处，各路径的加速度输入激励不明显，但是Path-4和Path-1的传递率均大于0.5，因此，Path-4和Path-1即发动机右前、左后的振动传递率存在一定的改进空间。

在441 Hz处，各路径的传递率函数均较小而加速度输入激励均较大，因此减振器在该频率处的减振性能也需要改进。

3 结 论

本文应用奇异值分解技术改进的OTPA方法，建立了从发动机到驾驶室座椅的OTPA模型，研究了挖掘机座椅振动的工况传递路径，得出以下结论：

(1) 模型合成的输出信号与实测的输出信号吻合较好，说明应用奇异值分解的OTPA方法能够有效地分析振动传递问题。

(2) 利用模型合成的座椅安装位置加速度信号频谱图，可以定位需要重点研究的频率；利用路径的振动贡献频谱图与矢量图，能够分析出特定频率处需要改进的路径；利用传递率函数频谱图和输入加速度频谱图，可以研究具体的改进方法。

(3) 20 Hz很可能是系统的共振频率，而发动机的1/2阶振动恰为20 Hz，应采取措施使这两个频率错开；80 Hz、441 Hz的加速度激励较大，考虑改进减振器在这些频率处的减振性能；221 Hz处，优先考虑降低发动机右前、左后的振动传递率。

[1] 庞剑，谌刚，何华．汽车噪声与振动——理论与应用[M]．北京：北京理工大学出版社，2006．

[2] Lei Liu. A frequency response function-based inverse substructuring approach for analyzing vehicle system NVH response [D]. Tuscaloosa: The University of Alabama, 2002.

[3] Koners G. Panel noise contribution analysis: An experimental method for determining the noise contributions of panels to an interior noise [C]//SAE Technical Papers：SAE International, 2003-01-1410.

[4] Dubbaka K R, Zweng F J, Haq S U. Application of Noise path target setting using the technique of Transfer Path Analysis [C]//SAE Technical Papers：SAE International, 2003-01-1402.

[5] 刘东明，项党，罗清，等．传递路径分析技术在车内噪声与振动研究与分析中的应用[J]．噪声与振动控制，2007,27(4)：73-77． LIU Dong-ming, XIANG Dang, LUO Qing, et al.Applying transfer path analysis to automotive interior noise and vibration refinement and development [J]. Noise and Vibration Control, 2007,27(4): 73-77.

[6] 慕乐，周鋐．基于传递路径分析的怠速工况下转向盘振动路径识别及改进[J]．汽车技术，2011(4)：15-17． MU Le, ZHOU Hong.Identification of steering wheel vibration paths and improvement in idle condition based on transfer path analysis [J]. Automobile Technology,2011(4):15-17.

[7] 赵彤航．基于传递路径分析的汽车车内噪声识别与控制[D]．长春：吉林大学，2008．

[8] Maia N M, Silva J M, Ribeiro A R. The transmissibility concept in multi-degree-of-freedom systems [J]. Mechanical Systems and Signal Processing, 2001, 15(1): 129-137.

[9] Gajdatsy P, Janssens K, Desmet W, et al. Application of the transmissibility concept in transfer path analysis [J]. Mechanical Systems and Signal Processing, 2010, 24(7): 1963-1976.

[10] Sitter G D, Devriendt C, Guillaume P, et al. Operational transfer path analysis [J]. Mechanical Systems and Signal Processing, 2010, 24(2): 416-431.

[11] 郭荣，裘剡，房怀庆，等．频域传递路径分析方法(TPA)的研究进展[J]．振动与冲击，2013,32(13)：49-55． GUO Rong, QIU shan, FANG Huai-qing, et al. Advance in studying on transfer path analysis methods in frequency domain [J]. Journal of Vibration and Shock, 2013,32(13): 49-55.

[12] Kakarala R, Ogunbonna P O. Signal analysis using a multiresolution form of the singular value decomposition [J]. Image Processing, IEEE Transactions on, 2001, 10(5): 724-735.

[13] Kohavi R. A study of cross-validation and bootstrap for accuracy estimation and model selection [C]//IJCAI-95. Proceedings of the Fourteenth Internatio．Montreal, Que., Canada, 20-25 Au, San Mateo, CA, USA：Morgan Kaufmann Publishers, 1995: 1137-43.

[14] De Klerk D. Dynamic response characterization of complex systems through operational identification and dynamic substructuring [D]. Delft: Technische Universiteit Delft, 2009.

[15] Reninger P, Martelet G, Deparis J, et al. Singular value decomposition as a denoising tool for airborne time domain electromagnetic data [J]. Journal of Applied Geophysics, 2011, 75(2): 264-276.

[16] 付俊涵．传递路径中声源串扰消除问题研究[D]．北京：北京交通大学，2012．

[17] Klerk D D, Ossipov A. Operational transfer path analysis: Theory, guidelines and tire noise application [J]. Mechanical Systems and Signal Processing, 2010, 24(7): 1950-1962.

Excavator seat vibration investigation based on operational transfer path analysis

PANG Xiao-ke1, ZHOU Yi-qi1, TANG Wei1, WANG Li1,2, MI Yong-zhen1

(1. Key Laboratory of High Efficiency and Clean Mechanical Manufacture, Ministry of Education, School of Mechanical Engineering Shandong University, Jinan 250061, China;2. School of Mechanical and Automotive Engineering, Qilu University of Technology, Jinan 250353, China)

The vibration of a new type of excavator prototype was inspected, and the vibration transmission from the engine to the cab seat was analyzed. The singular value decomposition (SVD) technique was applied to improve the method of operational transfer path analysis (OTPA). With the vibration test data under working condition, an OTPA model of vibration from the engine to the cab seat was built. The frequency domain features of the synthesized output signal agree well with those of the test output signal, so the model is proved valid. The key frequencies were revealed by analysing the synthesized output signal. The path necessary to be improved was identified in the light of all paths’ vibration contribution spectrum and vector diagrams. Some specific improvements were proposed in accordance with the spectrum analysis of transmissibility function and acceleration. The research provides an efficient engineering reference to noise or vibration transmission control.

OTPA; SVD; vibration contribution; transmissibility function

2013-12-19 修改稿收到日期：2014-04-30

庞晓柯 男，硕士生，1986年3月生

周以齐 男，博士，教授，博士生导师，1957年1月生

TB533+.1

A

10.13465/j.cnki.jvs.2015.09.031