大型商用飞机撞击刚性墙及核电屏蔽厂房的撞击力分析

林 丽， 陆新征 ， 韩鹏飞 ， 岑 松 ， 刘晶波

(1.清华大学 航天航空学院 工程力学系，北京 100084; 2. 清华大学 土木工程系，北京 100084)

大型商用飞机撞击刚性墙及核电屏蔽厂房的撞击力分析

林 丽1， 陆新征2， 韩鹏飞2， 岑 松1， 刘晶波2

(1.清华大学 航天航空学院 工程力学系，北京 100084; 2. 清华大学 土木工程系，北京 100084)

建立一个综合考虑了真实质量分布、刚度分布和材料模型的Boeing767-200ER模型，利用LS-DYNA程序对其撞击刚性墙进行数值模拟，获得了飞机撞击荷载时程曲线，并分析了不同初始速度及内部结构对飞机撞击力的影响；将该飞机有限元模型用于撞击核电站屏蔽厂房的数值模拟中，分析了靶体形状及相对刚度对飞机撞击力的影响，为飞机撞击核电站问题的深入研究奠定了基础。

核电站厂房；飞机撞击；数值模拟

自2001年“9.11”事件之后，核电站抵御飞机撞击的问题已引起了国际上的重视。例如，2009年6月12日，美国核管会颁布了新的联邦法规10CFR50.150“Aircraft Impact Assessment”，使抵御大型商用飞机撞击成为新建核电厂安全性评审的一项重要内容，该法规于当年7月13日正式开始生效[1]。然而飞机撞击核电站的过程十分复杂，涉及多个学科，目前仍有很多问题有待解决。其中，确定飞机撞击荷载函数就是一个至关重要的问题。

1968年Riera[2]提出著名的冲击力方程，为研究飞机撞击核电站问题提供了理论指导。该方程假设被撞击的混凝土结构变形相对飞机是非常小的，可以认为飞机撞击的是刚性体，将飞机看作一维模型，仅考虑飞机沿轴向的质量分布和压碎力，从而将飞机撞击刚性结构的撞击荷载分为惯性力和屈曲荷载两部分。

1993年，日本的Kobori研究中心、日本电能工业中心研究院和美国的Sandia国家实验室进行了鬼怪F4战斗机原型机对靶体的撞击试验[3]，撞击速度215 m/s，机身重量19 t。文献[3]公开了鬼怪战斗机的质量分布及压碎力。基于试验，得到了飞机对靶体的冲击力时程曲线，验证了Riera方法对于总撞击力计算的可靠性，并由此对Riera冲击力方程进行了修正。

然而，由于飞机撞击的全尺寸模型试验耗资大，实施困难，文献[3]是目前唯一公开的全尺寸模型试验。随着计算机的普及和有限元技术的发展，目前数值模拟成为研究该问题的主要手段。

数值模拟方法主要有两种：

(1) 非耦合方法：直接将荷载时程曲线加载到安全壳的假定作用截面上进行结构动力响应的数值模拟；

(2) 耦合方法：同时建立安全壳和飞机模型，对其撞击的全过程进行数值模拟。

无论采用哪种方法，飞机撞击力的获取都是一项重要的研究内容。一些常见商用客机的撞击力时程曲线已通过理论推导或数值模拟得到，如Boeing 707-320[2]、Boeing 747-400[4]、Airbus A320[5]，Boeing 767-400[6]，其撞击力时程曲线如图1所示。

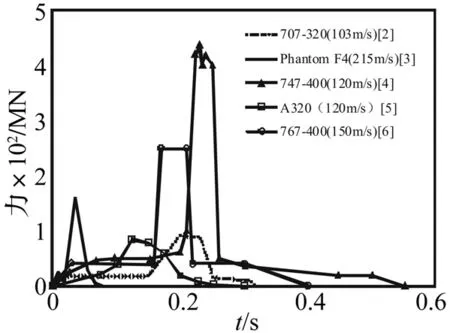
图1 不同型号飞机的撞击力时程曲线Fig.1 Impact force-time history of different aircrafts

然而，这些曲线仅针对某型飞机在某一特定速度下而言，实际飞机的结构、荷载分布情况千差万别，即便是同一类飞机，不同型号、不同使用用途下结果也会有所不同，一条撞击力曲线无法综合考虑这些问题，故应当对撞击力时程曲线的特点及影响因素等进行研究，掌握其内在规律。

本文建立了一个考虑真实质量分布、内部结构和材料模型的Boeing767-200ER模型，首先通过对刚性墙的撞击模拟，获得了飞机撞击荷载时程曲线，并以此验证了该有限元模型及碰撞模拟方法的合理性；之后对飞机撞击核电站安全壳的过程进行了数值模拟，进一步对撞击力进行分析。

1 飞机有限元模型

本文所采用的飞机模型为Boeing767-200ER，该飞机载客量224人(2级客舱布局)，是具有代表性的大型商用客机，在2001年的911事件中，撞向纽约世贸中心南北双子塔的两架飞机即为此型号。

本文所建立的飞机模型，主要参考波音公司对外公开的数据[7]、911事故分析相关文献以及飞机设计手册[8]：

(1) 几何外形与实际相符，如图2所示；

(2) 质量分配与实际相符，如表1所示。单边机翼重量24.12 t，发动机型号为通用CF6-80C2，重量4.366 t，机身(包括尾翼)总重为56.96 t[9]，考虑了内部设备而不考虑燃油的情况下，飞机重量为113.4 t；

(3) 考虑了飞机的主要结构，其结构尺寸按照真实情况或类似型号选取。除了机身蒙皮，还考虑了内部主要结构如机翼翼肋、尾翼翼肋、机身框、机身桁条及地板梁。

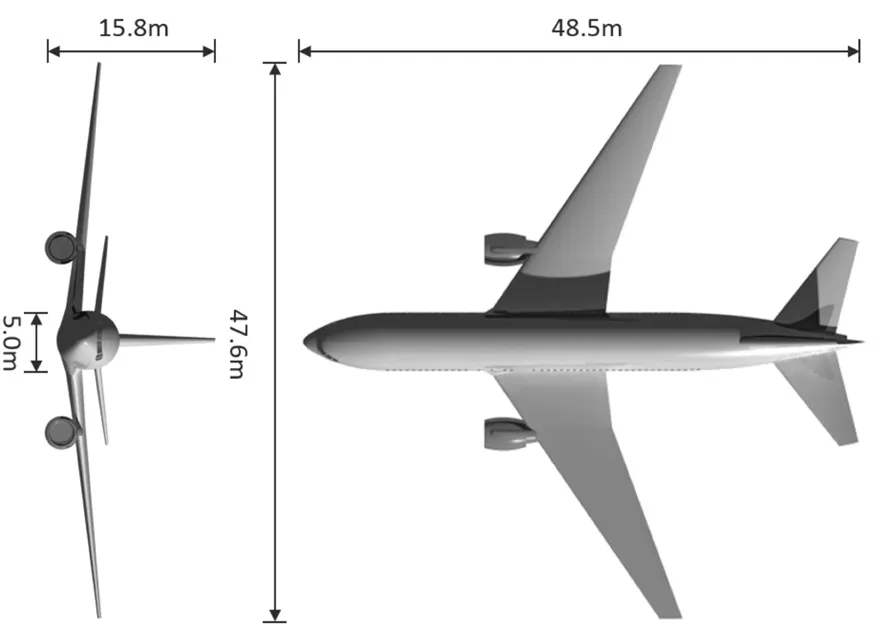
图2 Boeing767-200ER外形尺寸Fig.2 Overall dimensions of Boeing767-200ER

本文计算采用显式动力学软件LS-DYNA进行，飞机全局网格尺寸约为250 mm，壳单元和梁单元采用共节点建模：其中壳单元总数约5万，单元类型为SHELL163，采用Belytschko-Tsay单元算法，使用沙漏控制可进行一点积分，各部分壳单元厚度如表1所示；梁单元总数约为2.2万，单元类型为BEAM161，采用默认的Hughes-Liu截面积分，梁截面尺寸如表2所示。建立的飞机有限元模型如图3所示，其中图3(a)是飞机外部蒙皮壳单元，图3(b)是飞机内部结构的壳单元和梁单元。

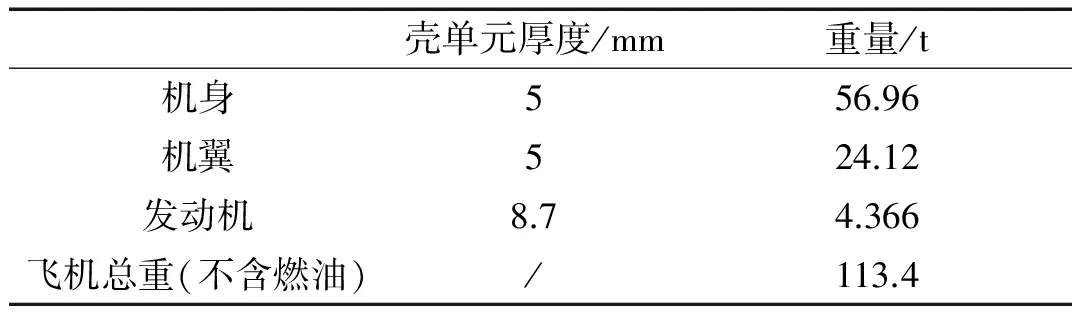
表1 飞机有限元模型参数

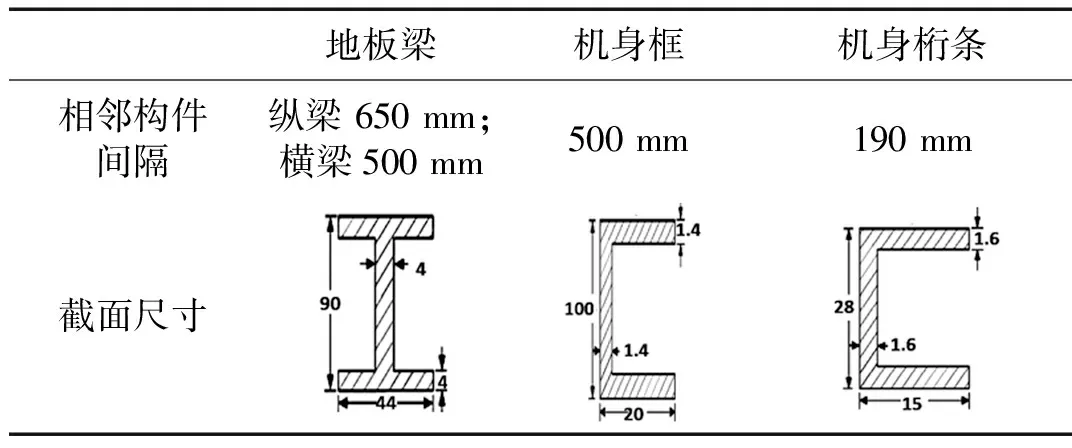
表2 内部梁结构参数

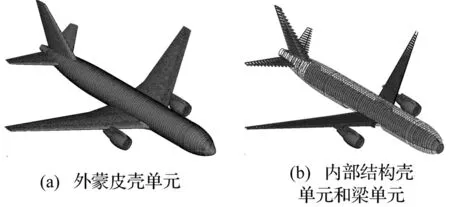
图3 飞机精细有限元模型Fig.3 Detailed aircraft finite element model

2 材料模型

2.1 JOHNSON_COOK模型(MAT015)

无论是飞机机身的铝合金材料还是发动机的钢材，在碰撞的情况下材料的率效应都是不可忽略的。对于金属碰撞问题，现在使用最为广泛的是JOHNSON_COOK模型(LS-DYNA中的MAT015)，很多文献均对该本构模型的参数进行了详细的研究。

JOHNSON_COOK是一个能反映应变硬化、应变率强化效应和温度软化效应的理想刚塑性强度模型。这个模型是由Johnson与Cook[10]在1983年提出来的，适用于描述金属材料在大变形、高应变率和高温条件下的本构模型(尽管本文尚未考虑爆炸火灾作用对碰撞过程的影响，但是采用JOHNSON_COOK模型为后续的考虑高温效应时的研究奠定了基础，这也是采用该模型的主要原因之一)，其表达式如下：

(1)

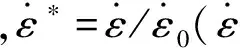
JOHNSON_COOK模型的断裂失效通过以下累积损伤法则确定:

(2)

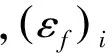
(3)

钢材和铝合金的材料属性如表3所示，JOHNSON_COOK模型参数如表4所示，采用的一致性量纲系统为长度(mm)、力(N)、质量(t)、时间(s)、应力(MPa)[9]。

表3 钢材及铝合金的材料属性

表4 MAT015参数

然而，LS-DYNA中JOHNSON_COOK模型不能用于梁单元，因此，本研究对壳单元使用JOHNSON_COOK模型，而对梁单元采用PLASTIC_KINEMATIC模型。

2.2 PLASTIC_KINEMATIC模型(MAT03)

PLASTIC_KINEMATIC模型对应LS-DYNA中的MAT03模型，也是常用的考虑了塑性流动、率效应和失效的金属本构模型，采用Cowper-Symonds模型来表示应变率效应对屈服函数的影响，其动态屈服函数如式(4)所示：

(4)

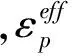
表5 MAT03参数

与MAT015的断裂失效法则不同，MAT03模型通过直接设定失效应变Fs来判断材料是否失效，因此MAT03模型需要输入的参数远少于MAT015模型，计算效率高，但是其失效应变如何选取缺乏相关的实验验证。为此，分别选取梁单元失效应变为0.05/0.1/0.2/0.4，比较其对飞机撞击力的影响(飞机初始速度设为200 m/s)，结果见图4。

由图4可见，梁单元材料失效应变的选取对撞击力影响很小，其撞击力曲线几乎重合，当失效应变取为0.05时，撞击力略大于其它三种情况，考虑到撞击的最不利情况，本文中取失效应变为0.05。

3 飞机撞击刚性墙的撞击力分析

3.1 初始速度对撞击力的影响

Boeing767-200ER飞机正常巡航速度为236 m/s，最大巡航速度为292 m/s，另外，考虑到飞机降落时的速度较低，最终我们选取了100 m/s、150 m/s、200 m/s、250 m/s及300 m/s这五种不同的速度下的撞击力进行比较。

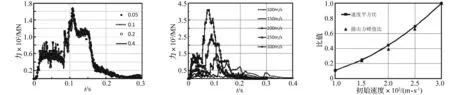
图4 梁单元选用不同失效应变时撞击力比较(200m/s)Fig．4Impactforceofdifferentfailurestrain(200m/s)图5 不同初始速度下飞机撞击力时程曲线Fig．5Aircraftimpacttimehistoriesofdifferentinitialvelocities 图6 撞击力峰值与初始速度平方的关系Fig．6Relationshipbetweenimpactforcepeakandinitialvelocity

从图5可以看出，初始速度越大，则撞击力峰值越高，且峰值出现时间越早，当初始速度为最大值300 m/s时，撞击力峰值达到410 MN。

为进一步说明撞击力峰值与初始速度之间的关系，令速度平方比RV2=(V/Vmax)2，撞击力峰值比Rpeak=P/Pmax。其中V是初始速度，Vmax是最大初始速度，即300 m/s;P是撞击力峰值，Pmax指初始速度300 m/s时所对应的撞击力峰值410 MN。图6中撞击力峰值比与初始速度平方比十分接近，说明撞击力峰值与初始速度的平方近似呈线性关系。

3.2 飞机结构对撞击力的影响

为分析飞机内部结构对其撞击力的影响，本文在原有限元模型的基础上进行简化得到了两个简化模型，分别命名为模型1、模型2，原模型则命名为模型3。三个模型各部位的重量分布情况一致，只是内部结构精细程度有所不同，其中模型3为最精确的模型(图3)，包括所有的梁单元和壳单元；模型2相对模型3，只建立了所有壳单元的模型，而没有相应的梁单元模型；模型1对模型2进一步简化，只有外层蒙皮的壳单元，而没有内部翼肋、地板、隔断舱板等结构的壳单元(见图7)。

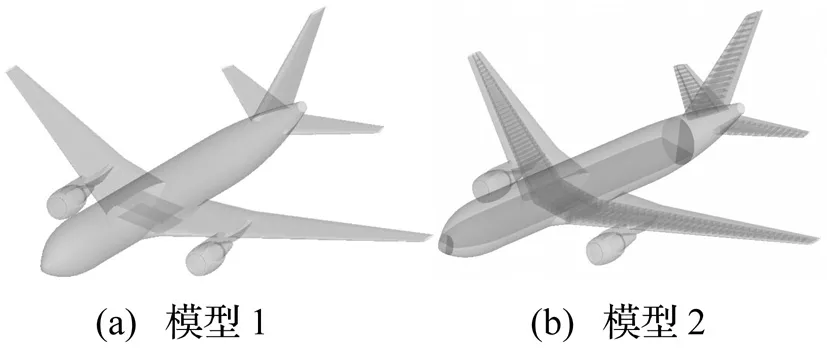
图7 不同精细程度的飞机模型Fig.7 Aircraft models with different level of details

本文针对100 m/s及150 m/s这两种初始速度下的三个模型的撞击力及冲量进行了比较，结果分别如图8及图9所示。

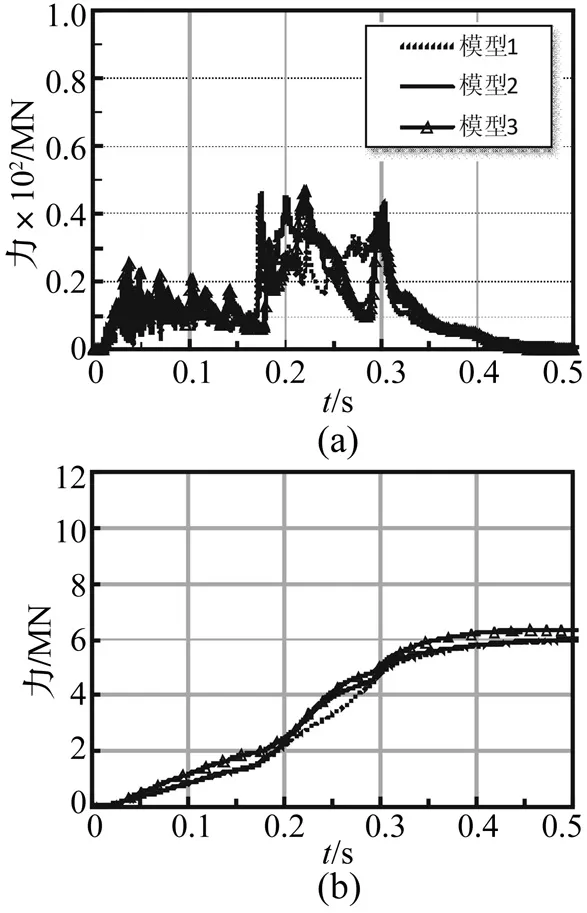
图8 模型1、2、3的撞击力及冲量时程曲线(100 m/s)Fig.8 Impact and impulse time histories of model 1/2/3 (100 m/s)

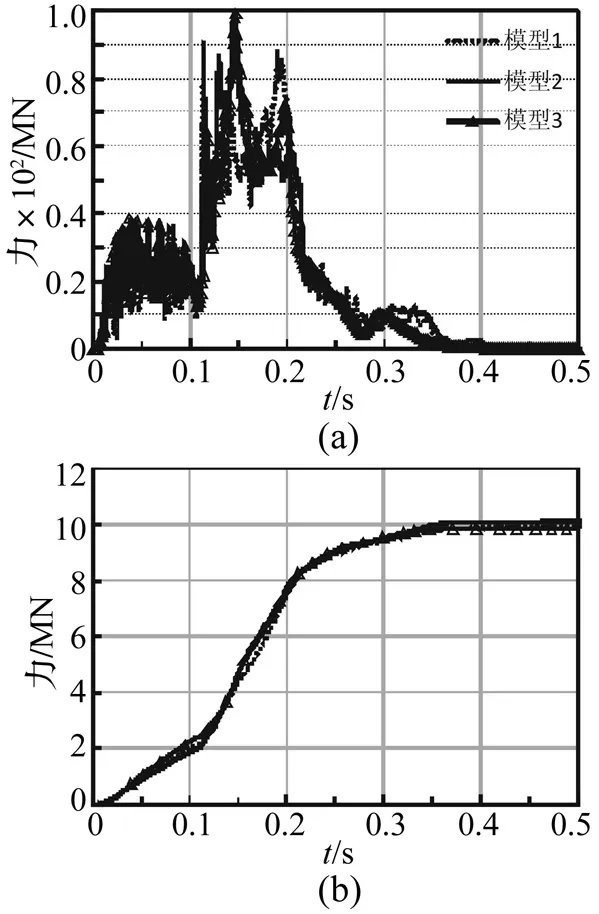
图9 模型1、2、3的撞击力及冲量时程曲线(150 m/s)Fig.9 Impact and impulse time histories of model 1/2/3 (150 m/s)

不同模型之间的撞击力时程曲线形状虽有一定差别，但峰值基本相当，而利用撞击力对时间进行积分得到对应冲量，可发现在初始速度为100 m/s时，模型1的冲量最小，模型3的冲量最大，相差约5%(见图8)，而当撞击速度增大至150 m/s时，这种差别变得很不明显，三个模型的冲量几乎一致(见图9)。

此组对比说明在较低的速度下，飞机结构对撞击力的影响较高速情况更为明显，而飞机袭击核电站时，离地高度很低，低速飞行的情况更有可能发生。因此，飞机内部结构对于撞击破坏的影响有必要给予考虑。实际上，在靶体是核电站安全壳而不是理想刚性墙时，飞机结构对撞击力的影响更为明显，这在下文中会进行详细的叙述。

4 飞机撞击核电站屏蔽厂房的撞击力分析

4.1 核电站有限元模型

本文建立了一个顶部为半球壳形，主体为圆筒形的核电站安全壳，混凝土厚度为1 m，两边均包裹了13 mm厚的钢板，其外形尺寸如下图所示。有限元模型采用共节点建模，即认为钢板和混凝土间具有可靠连接，忽略其相对滑移，全局网格尺寸为500 mm。

图10 核电站有限元模型Fig.10 Finite element model of NPP

钢板的材料模型为JOHNSON_COOK，具体参数同表3及表4中钢材的材料参数，混凝土采用Concrete_Damage_Rel3本构模型，混凝土单轴抗压强度为48 MPa。

4.2 靶体形状及刚度的影响

安全壳与飞机的接触面为一圆柱面，而不是刚性墙那样的平面，这将减小动量沿接触面法向的分量,并推迟发动机撞上安全壳的时间。为便于比较靶体的形状效应，先不考虑安全壳的变形，假设其与刚性墙同为刚性体。

如图11所示，对于撞击刚性墙工况，当T=0.09 s时，飞机发动机已撞击到刚性墙上，导致撞击力的忽然增大，而此时刚性安全壳还未受到发动机的撞击；类似的，对于撞击刚性墙工况，到T=0.15 s时，飞机的机翼已完成与刚性墙接触，这时撞击力突降，剩余的撞击力已经很小，而对于撞击刚性安全壳的情况，此时飞机机翼还有一大部分未与安全壳接触，撞击力下降趋势较缓。

靶体的这一形状效应也在图12的撞击力时程曲线中得以体现：

(1) 圆柱形靶体减小了动量沿接触面法线方向的分量，使得撞击力峰值下降；

(2) 圆柱形靶体推迟了发动机与其接触的时间，从而使撞击力峰值后移；

(3) 整个接触过程变得较为平缓，因此撞击力时程曲线的上升段和下降段均没有撞击刚性墙时那么“陡峭”。

而实际的安全壳并不是刚性体，其在飞机撞击下发生的大变形不可忽略。为分析靶体刚度对撞击力的影响，采用4.1节中建立的可变形安全壳与刚性安全壳承受的撞击力进行比较，在同样的飞机撞击条件下，其撞击力时程曲线如图13所示。

图11 靶体形状对撞击过程的影响 (200 m/s)Fig.11 Target shape effect on impact process (200 m/s)

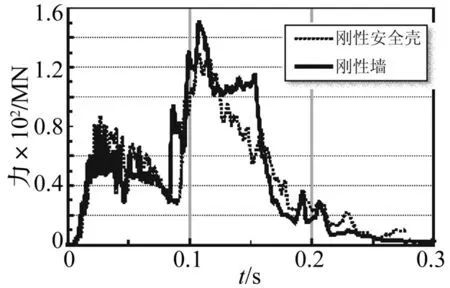
图12 靶体形状效应对撞击力时程曲线的影响 (200 m/s)Fig.12 Target shape effect on impact time history (200 m/s)

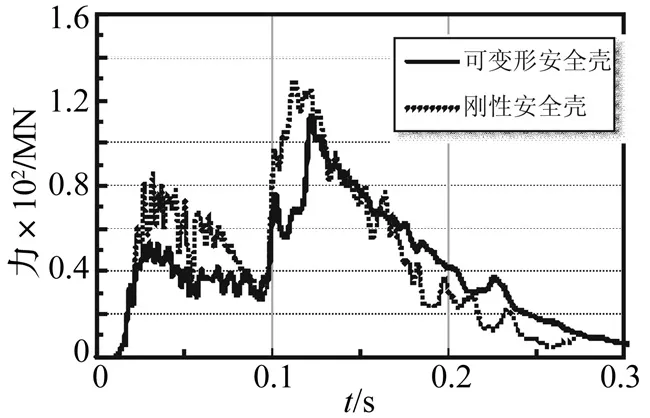
图13 靶体刚度对撞击力时程曲线的影响(200 m/s)Fig.13 Target stiffness effect on impact time history (200 m/s)

由图13可以看出，当靶体为刚性体时，两个撞击力峰值明显大于靶体为变形体的情况，说明靶体的刚度越大则撞击力峰值越高。

4.3 相对刚度的影响

3.2中比较了三个模型在撞击刚性墙时的撞击力差异，其差距大约为5%。这是因为，在撞击刚性墙的数值模拟中，由于墙体的刚度非常大，飞机的结构刚度变化显得很不明显。然而实际的核电站安全壳并不是理想刚性体，这时飞机结构刚度将对撞击力的产生更大的影响。

根据3.2中的结论，在初始速度较低时，飞机结构对撞击力的影响更明显。因此选取一个较低的初始速度100 m/s，分别对模型1、模型2、模型3撞击核电站安全壳的过程进行数值模拟。在T=0.45 s时刻，混凝土塑性应变如图14所示(由于定义了混凝土失效时的最大主应变，因此图中可以看到撞击区域混凝土由于发生大应变导致单元删除的现象)，可明显看出，随着飞机自身结构刚度的增加，安全壳受破坏的严重程度也增加，模型3撞击造成的破坏最为严重。

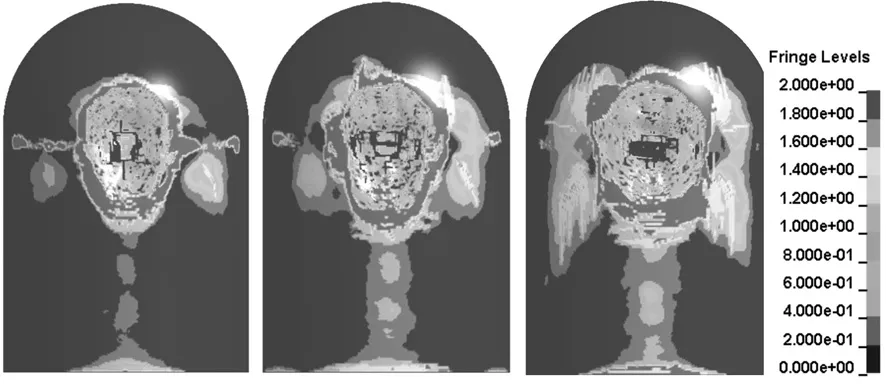
图14 T=0.45 s时混凝土的塑性应变(飞机初始速度为200 m/s;从左至右，依次是模型1、模型2、模型3撞击的结果)Fig.14 Concrete plastic strain atT=0.45 s (the initial velocity is 200 m/s; from left to right are model1/model2/model3)

图15比较了不同模型撞击力及冲量时程曲线，可见，模型2与模型3对安全壳的撞击力峰值明显大于未考虑内部结构的模型1；而从冲量来比较，模型1、2、3的冲量是逐步增加的，考虑了所有主要内部结构的模型3的冲量最大，与只考虑了外部蒙皮结构的模型1相差将近30%。

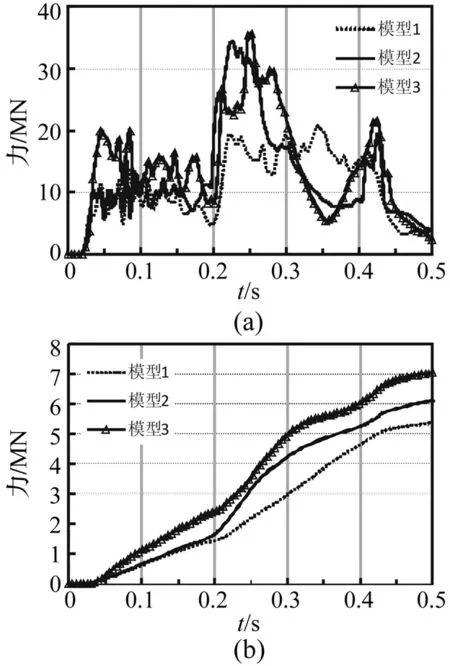
图15 模型1、2、3对安全壳的撞击力及冲量时程曲线Fig.15 Impact and impulse time histories of model 1/2/3

上述比较证明，撞击力确实与飞机自身刚度密切相关，当飞机结构刚度越大时，对安全壳的撞击破坏越严重。出于安全保证，在飞机撞击核电站的耦合计算研究中，建议采用模型3这样综合考虑了质量分布、刚度分布和材料模型的精细飞机有限元模型。

5 结 论

(1) 本文利用LS-DYNA程序对大型商用飞机撞击刚性墙进行了数值模拟，验证了飞机有限元模型及撞击模拟方法的合理性；说明了撞击力峰值大小与初始速度的平方近似呈线性关系；以及飞机结构对撞击力的影响在较低的速度下更为明显。

(2) 飞机撞击核电站安全壳的数值模拟结果说明了靶体的形状和相对刚度对撞击力有明显的影响：圆形靶体能够减小飞机动量的法向分量，因此能有效减小撞击力峰值；靶体刚度越大，则撞击力峰值越高；飞机相对于安全壳的刚度越大，则撞击力峰值和冲量也越大——由此也说明建立一个考虑内部结构的精细飞机有限元模型是十分必要的，文中关于飞机有限元模型建立的详细介绍及撞击力的分析结果旨在为今后此类问题的进一步研究提供参考。

致谢 感谢基金项目：大型先进压水堆核电站国家科技重大专项CAP1400安全评审技术及独立验证试验(编号：2011ZX06002-10)及国家自然科学基金(编号：51222804)和清华大学自主研究项目(2011THZ03)对本文工作的支持。

[1] 汤搏. 关于核电厂防大型商用飞机撞击的要求[J]. 核安全, 2010, 3(3): 1-16. TANG Bo. Discussion on the impact of large commercial airplane to nuclear power plant [J]. Nuclear Safety, 2010,3(3):1-16.

[2] Riera J D. On the stress analysis of structures subjected to aircraft impact forces [J]. Nuclear Engineering and Design, 1968, 8(4): 415-426.

[3] Sugano T, Tsubota H, Kasai Y, et al. Full-scale aircraft impact test for evaluation of impact force [J]. Nuclear Engineering and Design, 1993, 140(3): 373-385.

[4] Iliev V, Georgiev K, Serbezov V. Assessment of impact load curve of Boeing 747-400 [J]. MTM Virtual J.1,2011:22-25.

[5] Siefert A, Henkel F O. Nonlinear analysis of commercial aircraft impact on a reactor building[J]. Transactions, SMiRT, 2011, 21: 6-11.

[6] Jin B M, Lee Y S, Jeon S J, et al. Development of finite element model of large civil aircraft engine and application to the localized damage evaluation of concrete wall crashed by large civil aircraft [J]. Transactions of the 21stSMiRT, 2011.

[7] Boeing Commercial Airplanes. http://www.boeing.com

[8] 飞机设计手册总编委会.飞机设计手册[M].北京: 国防工业出版社, 2000.

[9] Karim M R, Fatt M S. Impact of the Boeing 767 aircraft into the world trade center [J]. Journal of Engineering Mechanics, 2005, 131(10): 1066-1072.

[10] Johnson G R, Cook W H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures [J]. Engineering Fracture Mechanics, 1985, 21(1): 31-48.

Analysis of impact force of large commercial aircraft on rigid wall and nuclear power plant containment

LIN Li1, LU Xin-zheng2, HAN Peng-fei2, CEN Song1, LIU Jing-bo2

(1. Department of Engineering Mechanics, School of Aerospace, Tsinghua University, Beijing 100084, China;2. Department of Civil Engineering, Tsinghua University, Beijing 100084, China)

A refined finite element model of Boeing767-200ER was developed, considering actual mass distribution, structural stiffness, and material properties. The rigid wall aircraft impact simulations were performed by using LS-DYNA program, to obtain the impact and impulse time histories, and analyze the effect of different initial velocities and airframes. The analysis of the aircraft impact on the concrete containment building shows that, the impact force and impulse by the aircraft are influenced according to the sectional shape and relative stiffness of the target. The analyses are necessary for further research on aircraft impact threats to NPP.

nuclear power plant (NPP); aircraft impact; numerical simulation

大型先进压水堆核电站国家科技重大专项CAP1400安全评审技术及独立验证试验(2011ZX06002-10);国家自然科学基金(51222804);清华大学自主研究项目(2011THZ03)

2014-01-08 修改稿收到日期：2014-04-25

林丽 女，硕士生，1989年生

陆新征 男，教授，博士，1978年生

O313.4

A

10.13465/j.cnki.jvs.2015.09.029