测力轮对状态估计计算方法研究

任 愈, 陈建政

(西南交通大学 牵引动力国家重点实验室,成都 600031)

测力轮对状态估计计算方法研究

任 愈, 陈建政

(西南交通大学 牵引动力国家重点实验室,成都 600031)

对轮轨间相互作用力的准确测量是监测列车运行安全状况的前提和基础。分析了测力轮对间断测量和连续测量方法，通过研究轮轨接触状态的变化特征，建立了轮轨接触力估计状态空间模型，提出基于状态估计的测力轮对轮轨力计算方法；在此基础上进行了仿真计算验证了算法的有效性，并在线路试验中以简单的间断测量测力轮对实现了轮轨力的连续测量。

测力轮对；状态估计；间断测量；连续测量

脱轨是列车运行中最危险的安全事故，也是列车提速中需要研究的关键问题之一。由于轮轨系统的实际运行行为复杂，影响脱轨的因素众多，至今对脱轨机理尚未完全掌握。但可以肯定的是，轮轨力变化是引起脱轨的直接原因。高精度的轮轨力检测，可以为脱轨机理研究、车辆动力学研究和列车安全检测提供重要的基础信息，对轮轨间相互作用力的准确测量是监测列车运行安全状况的前提和基础。

目前，最直接、最准确的轮轨力测量技术就是测力轮对方法，它以车轮作为轮轨力的检测传感器，在车轮辐板有限点处位置贴片组桥，通过测量应变信号实现轮轨接触力的检测。列车运行过程中，由于车轮和轨道间时变、非平稳的轮轨作用力和轮对转动对辐板应变信号的调制作用，使得辐板应变信号较为复杂。不同的组桥方式对应的计算方法也有所不同，从测量方式来看，主要分为间断式测量和连续式测量两种。

1 测力轮对测量方法

1.1 间断测量方法

间断测量实现方式和计算方法都相对简单，并且可以最大程度的避免横向力、垂向力和轮轨接触点位置三者之间耦合对应变信号的影响。目前在国内测力轮对实测试验中使用较多的是间断式的测力轮对。

间断式测量通过特殊的轮对制作方法，使特定电桥输出只受横向力或垂向力影响。其中，垂向桥输出如图1所示。

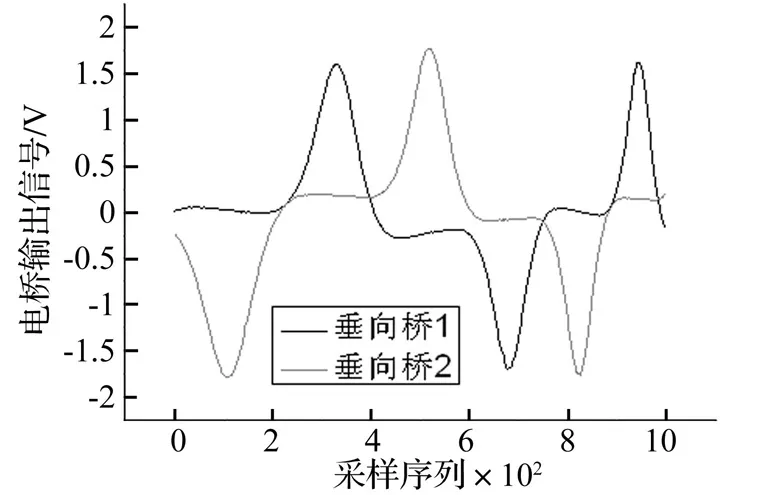
图1 垂向桥输出Fig.1 P-Force bridge output by discontinuous measurement

垂向桥输出波形中波峰和波谷交替出现，每个波峰和波谷之间轮对相位差为180°；同一辐板上两组垂向桥之间相位差为90°。通过搜索轮对旋转过程中数据的峰值，可以得到间隔角度为90°间断测量的间断点时间坐标，从间断点时间坐标取得间断点的横向桥和垂向桥输出，代入参数方程进行计算，得到间断点的轮轨横向力和垂向力。

间断测量方法实际上是一种近似的空间采样方法，采样频率为车轮转速的1/4，决定了其采样频率较低，其主要作用是用于评估列车运行中的一些关键参数(脱轨系数、轮重减载率等)，对于轮轨间的高频冲击很难进行有效测量；另外，如果频率较高的冲击发生在靠近实际间断点位置，很容易导致间断点位置判断不准确，从而影响间断测量计算结果精度。

1.2 连续测量方法

连续测量方法可以有效克服间断测量的弊端，是测力轮对技术的发展趋势。早期连续测力轮对方法是通过仿真和试验选择合适的组桥半径，分别建立横向桥、垂向桥和作用点位置桥，近似的认为轮轨接触力对车轮辐板应变的影响不耦合，其存在的问题是针对不同的轮对，需要设计不同的组桥方案，并且很难找到特别合适的贴片半径。

目前常用的方法是建立特定的应变桥，使电桥输出波形近似正余弦波形或三角波，通过特定方程进行计算[1-2]。如果不能得到良好的输出波形，一般利用三角函数关系式的性质将复杂的非线性方程组简化为线性方程组，通过计算得到轮轨作用力[3-4]。这种方法的问题是应变组桥方法繁琐，并且计算过程相对复杂，对检测精度和可靠性存在一定影响。

2 采样数据滤波分析

一般情况下，采用解方程组方式的测力轮对轮轨接触状态计算方法都是假设采集得到的应变桥输出信号即为应变信号真值。但是实际上，采集到的信号都叠加了相对高频的测试噪声，而噪声的来源包括多个因素，很难通过改进某一具体环节对其进行消除。

常规消除噪声干扰的方法是对测试信号进行选频滤波，以滤波后的数据进行计算。实际上，对于测力轮对这一特殊的应用环境，辐板电桥信号不仅受到轮轨力影响，也被轮对转动所调制，见图2。

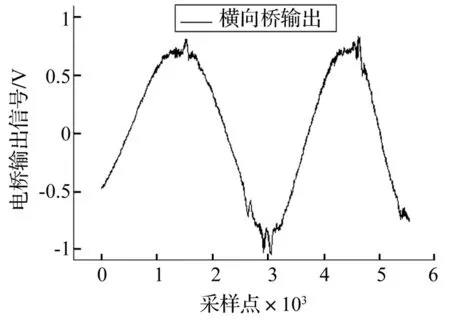
图2 间断式测力轮对横向桥信号Fig 2 Q-Force bridge output by discontinuous measurement

假定车轮辐板应变信号经过组桥后输出载波信号为较简单形式，即仅含有一次谐波z(t)=acos(ω0t)，同时将轮轨力描述为傅里叶级数形式：

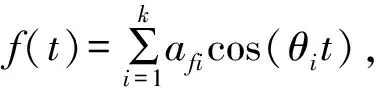
(1)

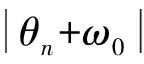
(2)

其中:k2>k1>k。由于ci为不可知量，其取值情况由车辆实际运行状态决定，滤波过程所产生误差是不可控制也不可量化的。设计采集设备时，也应将其选频截止频率设置为一个较高的频率。针对这种情况，考虑引入利用采样数据概率统计特性类的方法对测试数据进行处理。

3 轮轨状态空间处理方法

从信号测试的角度分析，轮轨接触力的变化是由车辆在行驶过程中受到随机激励引起的，而随机激励在任意不同时刻的取值之间都是无关的。而从微观的角度分析，在车辆行驶阶段的任意间隔较短时间内，轮轨接触状态在时间上存在一定的延续性。也就是说，在正常行驶状态下，只要保证采样频率相对于需要检测的轮轨力的频率足够高，则可以认为当前状态是在前一时刻状态基础上有一些规律性的变化。

3.1 状态空间方法

状态空间法(State-space Techniques)是现代控制理论中建立在状态变量描述基础上对控制系统分析和综合的方法[5-9]。状态变量是能完全描述系统运动的一组变量。如果系统的外输入为已知，那么由这组变量的现时值就能完全确定系统在未来各时刻的运动状态。状态空间模型是动态时域模型，以隐含着的时间为自变量。状态空间模型包括两个模型：一是状态转移模型，反映动态系统在输入变量作用下在某时刻所转移到的状态，如式(3)；二是量测模型，描述输出变量与状态变量和输入变量间的变换关系，如式(4)。两者构成了状态空间模型。

xk=f(xk-1,uk-1,vk-1)

(3)

yk=h(xk,vk)

(4)

3.2 测力轮对状态空间参数的确定

通过分析辐板应变输出与轮轨接触状态的关系，可以认为导致轮对应变桥输出改变的作用因素包括横向力Q、垂向力P、作用点位置X和轮对旋转角度θ，即可设轮轨接触状态向量为x=[Q,P,X,θ]T。设uk为状态的激励变化量，wk为状态转移噪声。在常规条件下，可以近似地假设轮轨接触状态变化为：

xk=xk-1+uk-1+wk

(5)

确定状态向量后，需确定各成员变量的递推规律进行统计和推导。

图3为在西南交通大学滚振试验台上进行的测力轮对滚动试验中的轮轨力输出，从图中可以看出在极短的时间内(一个采样周期)，每个采样点得到的轮轨力值相对于其前一个采样点有微小变化。由于轮轨力受未知轨道激励等各方面不确定因素的影响，其变化情况呈现出一定的随机性，一般考虑其服从高斯分布。

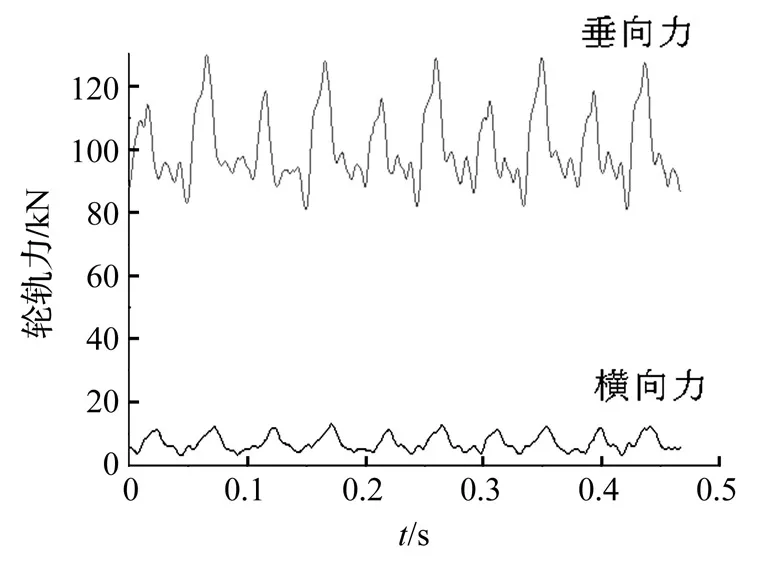
图3 滚振台试验轮轨力Fig.3 Wheel/rail force tested on the rolling and vibration rig

同样的，认为在较短的采样周期内，轮轨接触作用点在原作用点基础上发生一个随机变化。根据经验，在车辆正常运行时，作用点位置在名义滚动圆附近20 mm以内摆动，一般认为其变化服从高斯分布。

在较短的时间(轮对转动一周)内车速不会发生明显变化，即短时间内轮对转动角速度不会发生明显变化。可以将应变片组成间断测量的方式来取得轮对转动零角度时刻Ts和终止角度时刻Te，推导出在这段时间内轮对角速度ωθ，从而得到轮对转动角速度的估计ωθ=2π/(Te-Ts)。实际运行工程中车辆在运行过程中车速的变化(加速、减速过程及速度随机变化量)导致轮对转动角速度存在一个随机变化，设其模型如下:

θk=θk-1+ωθt+0.5aθt2+vθ

(6)

其中：ωθ是轮对转动角速度，aθ是轮对在车辆加减速行驶过程中的估计加速度，t为采样周期，vθ为服从高斯分布的随机变化量。根据实测试验，列车即使是在紧急制动的情况下，角加速度项的数量级远低于角速度项，一般可以忽略角加速度项的影响。

4 算法实现及验证

4.1 测力轮对仿真分析

辐板应变电桥的组桥输出是由上述四个状态因素的改变引起的，表示为：

sk=h(xk,vk)

(7)

其中：xk是当前状态向量，vk为量测噪声。对于组桥后的辐板应变信号，表示为：

si=gQ(θ)+gP(θ)+gX(θ)+wi

(8)

其中：gQ(θ)、gQ(θ)、gQ(θ)分别为横向力、垂向力和作用点位置对应变桥输出的影响。

式(7)和式(8)构成了测力轮对轮轨力检测的状态空间计算模型，测力轮对非线性方程组的计算问题转化为对于轮轨接触状态向量的估计问题。一般采用卡尔曼滤波类方法或粒子滤波类方法，卡尔曼滤波类方法一般处理线性或弱非线性估计问题，因此考虑采用粒子滤波类方法处理。

对于测力轮对轮轨力估计，观测方程对于最终估计结果精度有较大影响，而观测方程与组桥方式是对应的。另外，组桥方式的复杂程度也关系着测力轮对测试系统的复杂程度和可靠性；不同的观测方程意味着不同的测力轮对制作的复杂程度、可靠性和测试精度。通过仿真试验对比，在车轮辐板上的应变组桥方案中，最简单的组桥方式是对称片桥，但其输出的谐波成分较为复杂，估计轮轨接触状态结果精度最低；而谐波成分较为简单的信号估计结果精度较高，但其往往则对应着复杂组桥方式。

本文采用文献[3]中提到的保留一次和七次谐波的组桥方案对某动车组轮对进行有限元仿真，并通过标准粒子滤波(PF)、卡尔曼粒子滤波(EKPF)、无迹粒子滤波(UPF)三种方法对仿真应变桥输出进行状态估计计算，其结果如图4所示。

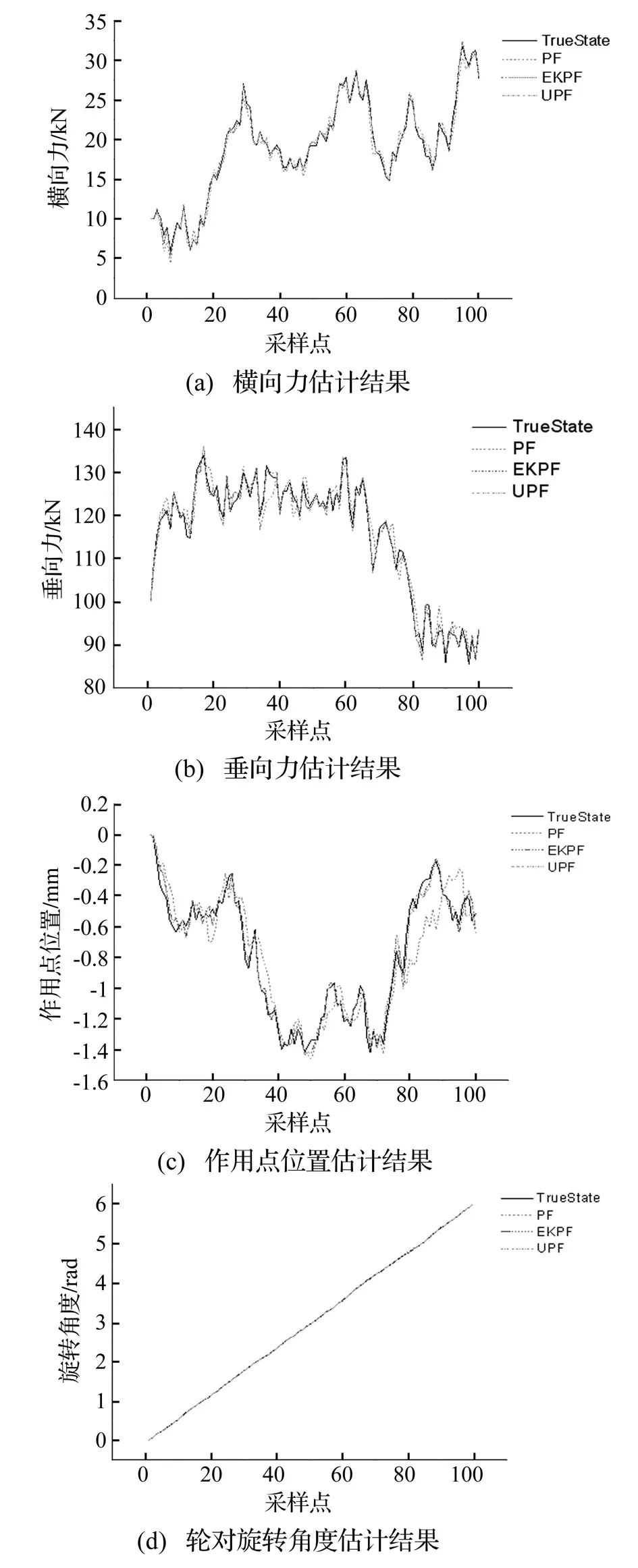
图4 仿真数据估计结果Fig 4 Estimation results

上述计算结果对应的均方根误差见表1。

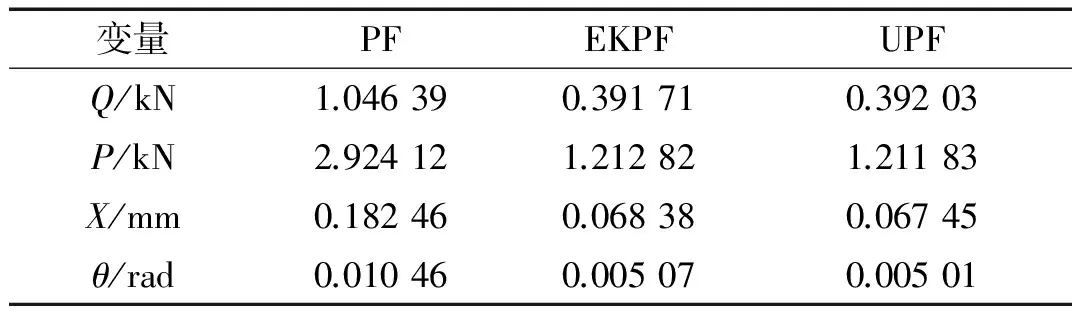
表1 仿真计算均方根误差

通过多次仿真计算，证明粒子滤波类方法能有效处理测力轮对轮轨力计算问题，其计算精度受设定参数和计算模型影响。在相同设定情况下，采用扩展卡尔曼粒子滤波方法和无迹卡尔曼粒子滤波方法优于标准粒子滤波算法，但计算复杂程度更大。

4.2 冲击信号跟踪

在车辆实际运行过程中，受到轨道不平顺激励及其它因素的影响(轨缝的冲击、经过道岔等)，轮轨力在受激的短时间内会产生剧烈变化，从而导致轮轨力状态转移过程不满足状态转移方程式中对力信号变化参数的假设，对含有垂向冲击信号的仿真数据计算结果误差见表2。

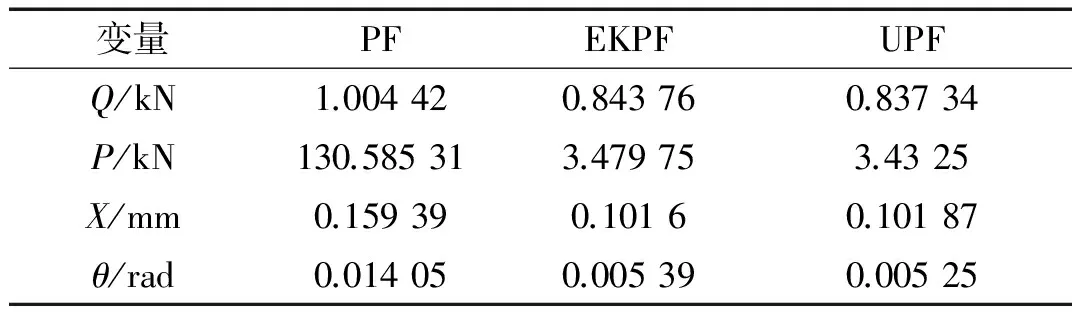
表2 冲击信号仿真均方根误差

可以看出，标准粒子滤波算法完全没有突变状态跟踪能力，垂向力计算产生了较大误差，而EKPF和UPF的估计结果明显优于标准粒子滤波算法，但估计结果的均方根误差值也有所增加。

在测力轮对轮轨力测试系统实际应用时，除了上面提到系统状态发生剧烈变化的问题，还存在着其它一些导致系统模型与实际情况产生误差的因素，如轮对不均匀、实际应用参数与标定数据产生误差、检测设备性能发生变化等。这些因素都会引起模型预测值和传感器测量值间的残差增大，需要相应提高滤波增益以提高估计精度。而EPF和UPF中的主要参数在运行前预先设置好，滤波增益完全通过EKF和UKF来求取，不能在线进行调整。文献[10]中周东华等提出正交性原理，证明通过在线选择一个时变的滤波增益阵，可形成一个具有算法鲁棒性、强跟踪能力和适中计算复杂性的强跟踪滤波器。

其核心特点为：① 在系统状态模型有一定的不确定性时，仍然具有较强的鲁棒性；② 在系统达到平稳状态时，对于突变和缓变状态都有极强的跟随能力。这对于前文提到的测力轮对检测中存在的问题有积极意义。

根据定义，强跟踪滤波器一般结构如式(9)：

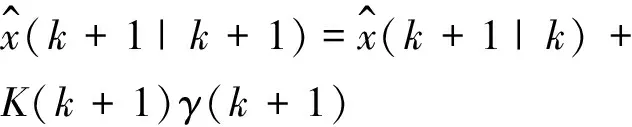
(9)

当存在一个满足式(10)和式(11)的时变增益矩阵K(k+1)时，滤波器(式(9))就成为一个强跟踪滤波器。

(10)

E{γ(k+1+j)γT(k+1)}=0,
k=0,1,2…;j=1,2,…

(11)

正交性原理通过条件式(11)表现出来，即要求不同时刻的残差序列处处保持相互正交。由于模型不确定性的影响，造成滤波器的状态估计值偏离系统的状态时，必然会在输出残差序列的均值与幅值上表现出来。这种情况下，通过实时调整增益矩阵，强迫式(10)仍然成立，使得残差序列仍然保持相互正交，则可以强迫强跟踪滤波器保持对实际的系统状态的准确估计。

采用强跟踪算法对上述含有垂向冲击信号的仿真数据进行计算，其垂向力误差如图5所示。

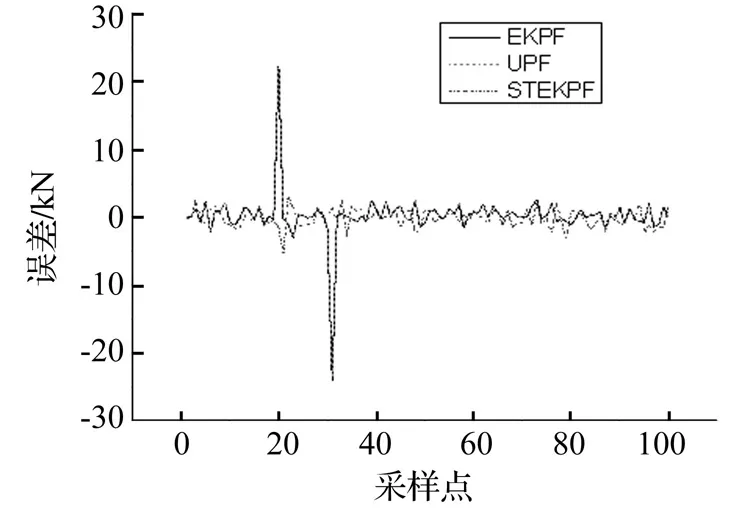
图5 垂向力估计误差Fig.5 P-Force estimation error

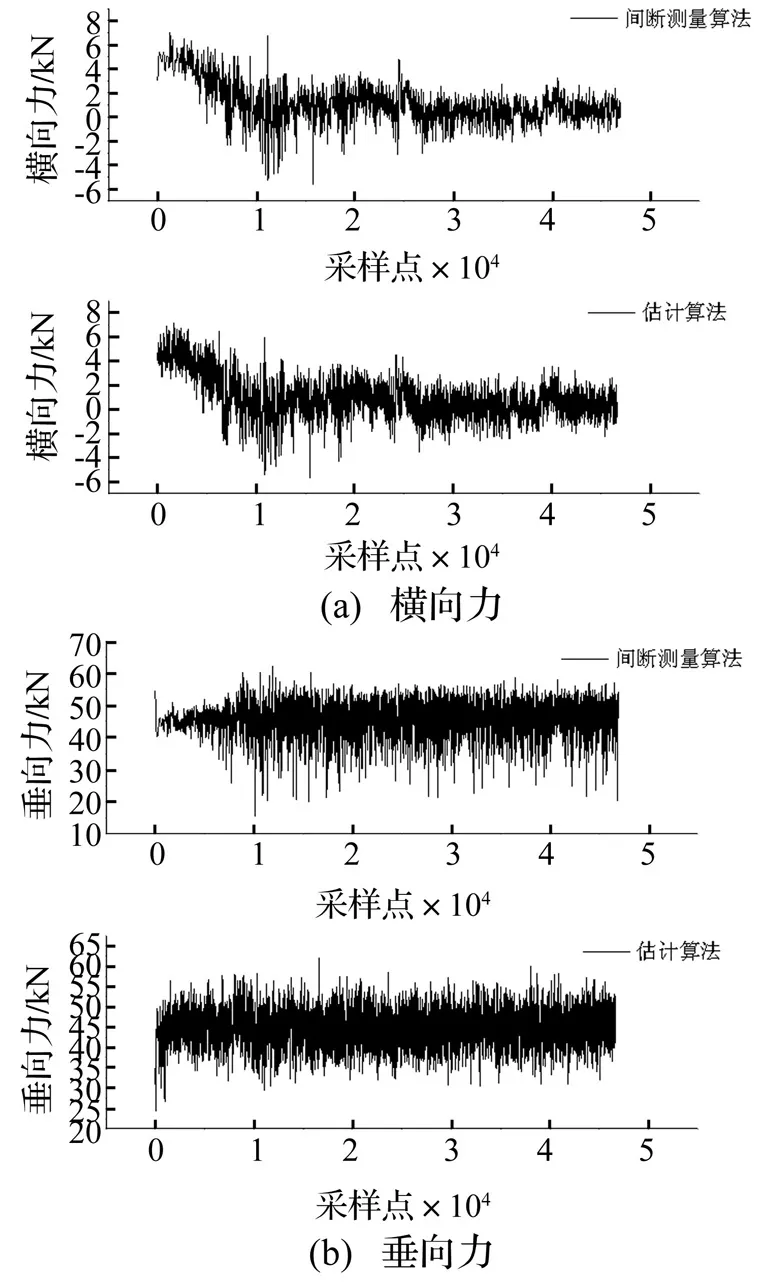
图6 线路试验计算结果Fig.6 Results of actual test

从图中对比可以看出，EKPF和UPF在状态突变的瞬间，计算结果产生了较大误差，而强跟踪算法可以迅速跟踪垂向力的变化，将误差控制在较小的范围。

4.3 线路实测试验验证

从前文所述可知，测力轮对状态空间估计算法的优点是无需建立复杂的三角函数方程组，对组桥方式也无特殊要求。在某动车组线路实测试验中，本文使用了组桥方式较为简单的间断测量测力轮对。图6为试验结果，分别通过间断测量和状态空间估计算法进行计算，并对其结果进行了比较。

从图6对比可以看出，间断测量结果和状态空间算法计算结果基本吻合。相对于插值得到间断测量结果，状态空间算法能利用所有采样数据，其计算输出频率远高于间断测量方法，有效扩展了间断测量测力轮对的检测频率。

5 结 论

本文根据轮轨接触力及其对应的辐板应变特点建立了测力轮对检测系统关于时间的离散递推模型，提出了测力轮对状态空间估计计算方法；通过对有限元仿真数据计算和线路实测试验对其进行了验证。试验结果表明，线路试验中以简单的间断测量测力轮对实现了轮轨力的连续测量，本文所提出的方法可行且易于实现。另外，间断式测力轮对仍需对辐板进行加工，给测力轮对的制备带来一定的困难，笔者将在组桥方式和数据处理方法上做进一步的研究。

[1] Modransky．Instrumented locomotive wheels for continuous measurements of vertical and lateral loads[J]．ASME Publication,1980,79-RT-8.

[2] 曾宇清，王卫东，甘郭文，等. 测力轮对连续测量的理论与实践[J]．铁道学报,1998, 20(6):28-34. ZENG Yu-qing, WANG Wei-dong, GAN Dun-wen, et al. Theory of high accuracy load measuring wheelset[J]. Journal of the China Railway Society,1998, 20(6):28-34.

[3] 陈建政. 轮轨作用力和接触点位置在线测量理论研究[D].2008.

[4] 侯卫星，王卫东，曾宇清. 高精度高速连续测量轮轨动态作用力的研究[J].铁道学报, 2010, 32(1): 24-29. HOU Wei-xing, WANG Wei-dong, ZENG Yu-qing. Research on high-precision,high-speed and continuously measured dynamic wheel-rail forces[J]. Journal of the China Railway Society, 2010, 32(1): 24-29.

[5] Nrgaard M. Developments in state estimation for nonlinear system[J]. Automatica, 2000, 36(11):1627-1638.

[6] Julier S J, Uhimann J K, Durrant-Whyte H F. A new method for nonlinear transformation of means a and estimators[J]. IEEE Trans Automatic Control, 2000, 45(3):477-482.

[7] Christophe B, Laurent T, Jean G. EKF and particle filter track to track fusion:a quantitative comparison from radar/lidar obstacle tracks[C]. In Proceedings of 8th International conference on Information Fusion, Philadelphia, PA, 2005 July, 2:1303-1310.

[8] Wan E, Merwe R V D. The unscented kalman filter for nonlinear estimation [A]. In: Proc of the Symposium 2000 on Adaptive System for Signal Processing, Communication and Control(AS-SPCC) [C]. Lake Louise, Alberta, Canada, October,2000, 1: 489-494.

[9] Merwe R V D, Doucet A, Freitas N D, et al. The unscented particle filter[R]. Cambridge University Enginnering Department, England Cambridge University press, 2000: 1-45.

[10] 文成林，周东华.多尺度估计理论及其应用[M].北京：清华大学出版社,2002.

Wheel/rail force calculation method based on state estimation

REN Yu, CHEN Jian-zheng

(Traction Power State Key Laboratory, Southwest Jiaotong University, Chengdu 610031, China)

Accurate measurement of wheel/rail force is the premise and basis of monitoring the train operation status. The discontinuous and continuous measurement methods of instrumented wheelset were analysed, the variable characteristics of wheel/rail contact state were studied, the space model for wheel/rail contact force state estimation was established and the wheel/rail force calculation method based on state estimation was proposed. The algorithm was verified by simulation calculations. Moreover, a continuous measurement was achieved in actual track test by using a simple discontinuous instrumented wheelset.

instrumented wheelset; state estimation; discontinuous measurement; continuous measurement

国家自然科学基金青年科学基金项目(51405404)

2014-01-08 修改稿收到日期：2014-05-20

任愈 男，博士，助理研究员，1981年生

U270.7;U216.3;TH721

A

10.13465/j.cnki.jvs.2015.09.020