塔式容器新型扰流减振方法研究

谭 蔚, 李晓琳, 吴 皓

(天津大学 化工学院，天津 300072)

塔式容器新型扰流减振方法研究

谭 蔚, 李晓琳, 吴 皓

(天津大学 化工学院，天津 300072)

基于塔式容器发生横风向振动的原理，设计了适用于防止塔式容器横风向振动的声波扰流器和喷射扰流器。利用有限元分析软件ANSYS Workbench14.0 建立三维流固耦合数值模型对比分析了两种扰流器在不同扰流速度和扰流频率情况下对塔体周围边界层的干扰效果。结论是速度取一阶临界风速，频率取剪切层不稳定流的脉动频率时，两种扰流器的扰流防振效果最好；同样的扰流参数情况下，喷射扰流器的扰流防振效果比声波扰流器的好。此研究结论为塔器防振措施中扰流器的设计与工程应用提供参考和依据。

横风向振动；扰流器；有限元分析；流固耦合

钢制塔式容器是石油化工行业常见的一种的高耸结构，具有刚度小、外形细长等特点。在生产应用中，塔式容器多安装在室外，非常容易受到环境风载荷的作用，在两个方向上产生振动：一种是顺风向的振动，振动的风向与风的流向一致；另一种是横风向的振动，振动的方向与风的方向垂直，也称风的诱发振动，后者往往在塔式容器的风致振动起主导作用[1]。

随着工业需求的提高和科学技术的进步，塔式容器日益向着更高、更轻、更柔的方向发展，使其对风荷载的敏感性进一步增强。近几十年来，塔振动的事故频繁发生。我国的炼油化工厂中曾发生塔顶振幅高达1.4 m的塔设备振动事故[2]！塔设备振动事故对于整个流程的产品生产和质量保证等方面有很大的影响。因此风诱发振动和防振的研究受到各国工程界与学术界的重视。应用于工程设计的减振对策已被提出，其中添加扰流设备是非常重要的一种减振措施[3]。

传统的扰流设备如外围框架、螺旋式或轴向式翅片，用以干扰或破坏塔体周围卡门涡街的形成，从塔体横风向振动的源头上减振或防振。已经纳入应用的是翅片扰流法，即在塔器外壁上段1/3高度内安装螺旋式或轴向式翅片，但塔式容器通常有外保温层并有多种附件，所以不便工程实施[4]。本文提出两种新型的扰流防振装置，并用数值模拟的方法对二者的扰流防振效果进行了对比分析，对于防止塔式容器风诱发振动的新的扰流措施的探索和研究具有一定的借鉴和指导意义。

1 声波扰流器的设计

1.1 声波扰流器的设计原理

声波是一种传递在弹性媒介(例如空气)中的振动形式。声波的传递过程附带有能量的传递，根据声源振动速度和振动频率的不同，其所传递的能量也不同。声波的传递过程在组成媒质的分子的杂乱运动中增加了一个有规律的运动，使组成媒质的微元体的压力、密度和质点速度等有所改变，从而改变媒质在空间和时间上的能量分配。从上个世纪60年代，国外学者们就发现圆柱绕流的分离边界层对于外加扰动，例如机械振动或声刺激，是敏感的。所以当固定于塔体上的声波扰流器作用于塔设备周围的空气场时，会影响其分离剪切层中空气微元体的能量分配，造成分离剪切层内部不稳定流的扰动，进而破坏了塔体下游尾流的规则性涡街，改变旋涡脱落频率使其远离“共振点”。

1.2 声波扰流器的设计

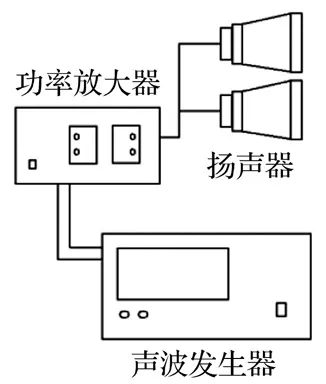
图1声波扰流器的结构Fig.1 Structure of the acoustic turbulator

声波扰流器由三个部分组成，其结构图如图1。

声波发生器，发出与所设定声波信号相对应的交流电信号，并将信号通过连接线传递到功率放大器。通过调节输出电压的大小和频率可以改变声波的声压幅值和频率。 功率放大器，在给定失真率条件下，能产生最大功率输出以驱动下游的扬声器发射所需声波，是声波发射器和扬声器之间的“桥梁”。 扬声器，将功率放大器传递过来的交流电信号转化成声波并将其发射，是声波扰流器的直接功能部件。其数量可以根据实际需要作调整。

声波发生器发射出的周期性声波信号可以用声压方程表示为：

(1)

其中：Z代表声阻抗，kg·m-2·s-2；Ua代表声波的振速，m/s；ωa代表声波的振动角频率，ωa=2πfa，fa是声波的频率，Hz；u是声波在空气中的传播速度，m/s。

2 喷射扰流器的设计

2.1 喷射扰流器的设计原理

塔器的诱导振动在本质上还是曲面物体外部绕流的问题。绕流边界层的分离导致旋涡的交替性产生和脱落，由此产生横风向周期性的升力。在升力的作用下塔体发生横风向受迫振动。当旋涡脱落频率和塔体的固有频率相同时，振幅达到最大值，系统便发生共振，即塔的风诱导振动；而当旋涡脱落频率和塔体的固有频率差值增大，塔体振动的振幅减小，振动减弱。 对于钝体绕流减振的研究，重点就是对边界层分离的控制。本文提出的喷射扰流器，是在塔体壁面的特定位置设置喷头，喷射出周期性变化的脉冲气流以改变边界层内流体的能量分配从而干扰边界层的分离，进而改变旋涡脱落频率，使得旋涡脱落频率远离塔体的固有频率，达到减弱或防止塔设备风诱导振动的目的。

2.2 喷射扰流器的设计

喷射扰流器大致可分三个部分，其结构图如图2。

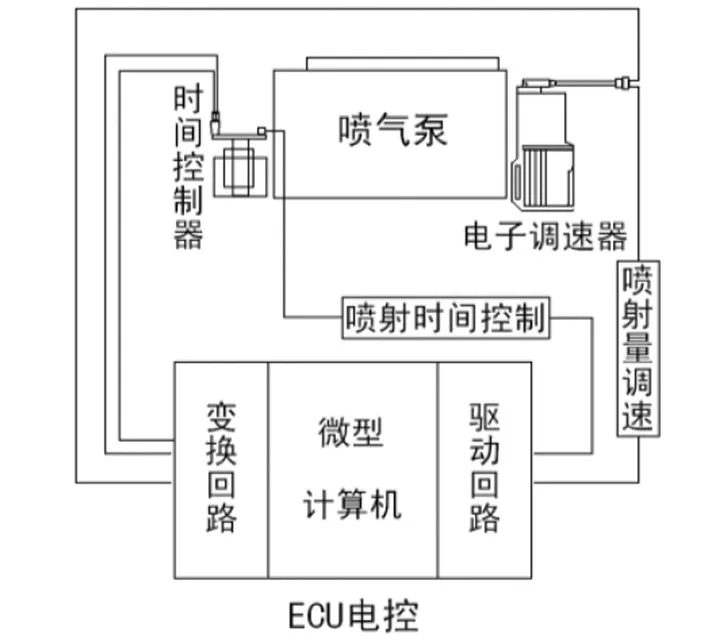
图2 喷射扰流器结构Fig.2 Structure of the eject turbulator

ECU电控单元，内设连通驱动回路和变换回路的微型计算机，根据负荷指令和设定的脉冲信号，确定相应控制参数，通过驱动回路传达信号至连接着喷气泵的电子调速器和时间控制器，从而控制喷气泵的气流喷射，获得所需要的喷射扰流效果。

喷气控制装置，包括电子调速器和时间控制器。电子调速器采用ECU控制电动机，电动机控制供气齿杆，从而控制喷气量；时间控制器内设轴向布置的气压活塞，活塞带动后续传动系统改变喷气泵的驱动轴，同时时间控制阀通过电磁阀受控于ECU，从而控制了喷气时间。

喷气泵，在喷气控制装置的控制下从周围大气中吸气与喷气，实现脉冲式气流喷射。

喷射扰流器发出的周期性脉冲气流可以表示为周期性的矩形脉冲速度激励，在一个周期(0，Tm)内的时域表达式为：

(2)

其中，Um代表的是周期性脉冲信号的速度幅值，m/s；Tm代表脉冲周期，s；对应的脉冲频率为fm=1/Tm，Hz。

3 扰流防振的数值模拟

本文利用ANSYS Workbench14.0软件对某二甲苯塔[5]进行扰流防振的数值模拟，以期分析两种扰流器的防振效果。考虑到塔式容器的扰流防振涉及到流体域和固体域的相互耦合作用，所以选择三维ANSYS-CFX耦合。本文模拟的塔式容器绕流问题的雷诺数为5.67×106，属于超临界区范围，此时的绕流场具有明显的三维特征，需要考虑复杂的湍流涡动影响，所以湍流模型选用大涡模型(LES)。采用的亚格子尺度模型为wale模型，其中常数Cw为0.325。

3.1 模型几何和边界条件

塔在空塔工况下最容易发生诱导振动，所以本文的防风振模拟是以空塔状态进行分析的，流固耦合模型的主要参数如表1，几何结构及边界条件设定如图3。声波扰流器在数值模拟中已被证实可以简化为余弦速度激励[6]，而喷射气流可以简化为脉冲速度激励，在软件中可以通过CEL语言编入。

表1 模型的基本参数 (单位：m)

图3 计算模型结构及边界设置Fig.3 Computation model structure and boundary conditions

图4 塔体壁面声波扰流器布置图Fig.4 Position of turbulators on column surface

图5 网格划分Fig.5 Meshing

本文设计三组六个扰流器分别被安置在塔体表面0.93、0.85和0.77塔高处来激励柱体周围的分离剪切层。每组扰流器在横截面的位置如图4所示，扰流器与来流方向的夹角为90°，该方向被证实是最优扰流方向[7]。

3.2 网格划分

数值计算

的网格划分如图5所示，模型全部采用六面体结构化网格以保证精度，并对塔周边网格进行了局部细化。网格总数118万。

4 结果与讨论

为了考察增加扰流器前后的扰流效果，数值模拟对设置扰流器前后塔体绕流场的旋涡脱落频率fv、塔体壁面压力系数分布Cp和边界层分离角θs这三个主要流场特征量进行了对比和分析。边界层分离角θs对应塔壁面摩擦系数为0的分布角的值。

(3)

其中:Ff是塔体所受的壁面摩擦力，N；p为流场静压，Pa；p0为入口来流静压，Pa；A为塔体的参考特征面积，一般取A=H×d，m2；H为塔体的高度，m；fv，旋涡脱落频率，Hz；St为斯特罗哈数，在Re=5.67×106时接近0.27；U为来流速度，m/s。

为了描述方便，定义声波频率或脉冲频率与不设扰流器时绕流场旋涡脱落频率的比值为扰流频率比fr，扰流频率比的取值是由Bloor、Wei & Smith、Kourta、Norberg等实验回归曲线总结的剪切层频率经验公式[8]确定；声波振速或脉冲速度幅与来流速度的比值为扰流速度幅值比Vr，考虑扰流速度幅值比太大会影响扰流器稳定性，速度比控制在0～1的范围内。

由JB4710-2005《钢制塔式容器》[9]中相应的公式计算可知塔顶处的最高风速为52.3 m/s。模态分析可得塔的一阶固有频率为0.443 Hz，塔的二阶固有频率为2.69 Hz，其对应的临界速度分别为12 m/s和72.8 m/s。塔可能受到的最大风速小于二阶临界风速，所以计算中只考虑一阶共振。数值模拟设置来流分别为0.692*12*z0.16(按JB4710中B类地面风速设定)和均匀来流12 m/s，设置时间步长0.001 s，总模拟时间34 s。其中，z为离开地面的高度，m。对比两种进口速度条件下的三个主要流场特征量，可知两者的旋涡脱落频率、压力系数和分离角分别只相差0.05%、2.19%和1.65%。由于本文研究的塔器高度较高，总体而言塔上部速度变化不大，所以设置进口速度为均匀来流已可以反映绕流场特征。

4.1 设置扰流器前后的旋涡脱落频率

来流速度为12 m/s时，在塔体表面增设频率比fr固定为522.54，扰流速度幅值比变化的两种扰流器。图6是未增加扰流器和在塔体分别增加不同速度的声波扰流器升力系数的功率谱分析图，由图可知随着扰流速度比从0增大到1，旋涡脱落频率降低，减振效果增强。在塔体分别增加不同速度的喷射扰流器升力系数的功率谱分析图和不同频率比的声波扰流器和喷射扰流器的功率谱分析图与图6类似，不予赘述。图7是综合功率谱分析所得的不同速度比情况下旋涡脱落频率对比图。

图6 不同速度比工况的功率谱密度Fig.6 Comparison of power spectral density for cases with different Vr

图7 不同速度比工况的旋涡脱落频率Fig.7 Comparison of vortex shedding frequency for cases with different Vr

同样来流速度，增设速度幅比值Vr固定为0.75而扰流频率比变化的两种扰流器。图8是综合频谱分析和功率谱分析所得不同频率比情况下旋涡脱落频率对比图。

图8 不同频率比工况的旋涡脱落频率Fig.8 Comparison of vortex shedding frequency for cases with different fr

未设置扰流器时，由本文流固耦合模型计算所得的绕流场旋涡脱落频率为0.439 5，与塔体的固有频率是非常接近的，本文数值模型可以准确模拟绕流情况。

分析图6～8可知，设置两种扰流器能够有效减小绕流场旋涡脱落频率。并且随着扰流速度比和扰流频率比的增加，设置两种扰流器的情况下旋涡脱落频率的变化规律是一致的。扰流速度比增大，旋涡脱落频率减小；频率比fr为771.11时旋涡脱落频率最小。同样，对于特定的一个工况，设置喷射扰流器比声波扰流器情况下旋涡脱落频率更小。

4.2 设置扰流器前后绕流场的摩擦系数分布

图9是来流速度为12 m/s时不设置任何扰流装置的塔体外壁面的摩擦系数分布曲线。由摩擦系数分布曲线计算得分离角为138.3°。

图9 设置扰流器前摩擦因数分布Fig.9 Distribution of friction coefficient without disturbances

来流速度为12 m/s时，在塔体增设扰流频率比fr固定为522.54，扰流速度幅值比变化的两种扰流器。未增加扰流器和在塔体分别增加不同速度的声波扰流器和喷射扰流器的分离角对比如图10所示；同样来流速度，在塔体增设速度幅比值Vr固定为0.75而扰流频率比变化的两种扰流器。未增加扰流器和分别增加不同频率比的声波扰流器和喷射扰流器的分离角对比如图12所示。由图10、11分析可知，扰流器干扰了塔体周围流场，导致边界层的提前分离。分离角随扰流速度比和扰流频率比的变化规律与绕流场旋涡脱落频率的相同。

4.3 设置扰流器前后绕流场的压力系数分布

来流速度为12 m/s时，在塔体表面增设频率比fr固定为522.54，扰流速度幅值比变化的两种扰流器。未增加扰流器和在塔体分别增加不同速度的声波扰流器和喷射扰流器的压力系数分布对比如图12所示；同样来流速度，增设速度幅比值Vr固定为0.75而扰流频率比变化的两种扰流器。

未增加扰流器和在塔体分别增加不同频率比的声波扰流器和喷射扰流器的压力系数对比如图13所示。

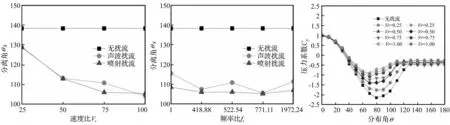
图10 不同速度比工况的分离角对比Fig．10ComparisonofseparatedangleforcaseswithdifferentVr图11 不同频率比工况的分离角对比Fig．11Comparisonofseparatedangleforcaseswithdifferentfr图12 不同速度比工况的压力分布对比Fig．12ComparisonofpressurecoefficientforcaseswithdifferentVr

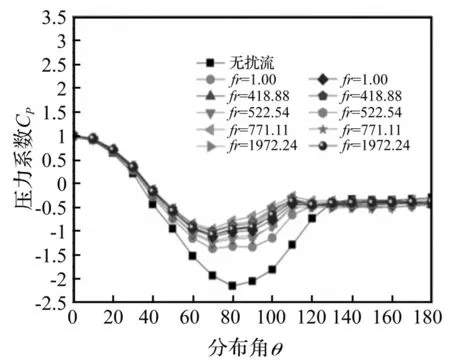
图13 不同频率比工况的压力分布对比Fig.13 Comparison of pressure coefficient for cases with different fr

由图12、13分析可知，扰流器的干扰作用使得塔体周围流场的压力差减小。压力系数分布随扰流速度比和扰流频率比的变化规律与前两个流场特征量的相同。

综合以上三个流场特征量的变化来看，设置声波扰流器和喷射扰流器后塔体绕流场的边界层分离角、塔体表面压力差和旋脱脱落频率都减小，这说明扰流器对塔体绕流场有显著的干扰作用。且扰流速度幅值比为1，扰流频率比为711.11时，扰流效果最佳；速度比和频率比取同一值时，喷射扰流器的扰流作用强于声波扰流器。

5 结 论

本文在对塔式容器的风诱发振动理论和工程实践防振措施进行研究分析的基础上，提出两种新型的扰流防振方法，并且设计了声波扰流器和喷射扰流器的结构。在此基础上建立了三维双向流固耦合模型来对比分析两种扰流器在塔式容器防风振的作用，得到以下结论：

两种新型扰流器都能够有效扰流防振，塔体绕流场边界层分离角越小，旋涡脱落频率越小，距离塔体的固有频率就越远，则引发共振的可能性也越小。同时，设置扰流器以后塔体表面的压力差也有明显的减小，这样会使得塔体壁面的合力减小，阻力系数和升力系数也相应地减小。

在一阶临界风速范围内，扰流速度增大，声波扰流器和喷射扰流器的扰流振效果都加强。所以在实际应用中，扰流器的扰流速度取一阶临界风速时，防风振效果最好。在本文确定的频率比范围内，扰流器的扰流频率取771.11倍的无扰流旋涡脱落频率时的扰流防振效果最佳，这是因为此时扰流频率最接近塔体分离剪切层中不稳定流的脉动频率。

总体来看，在扰流速度和扰流频率相同的情况下，喷射扰流器比声波扰流器的的防振效果好。首先，气流扰动和声波扰动对于塔体分离边界层的作用原理是不同的；其次，扰动信号的不同对于扰流防振效果也有影响。工程应用中应根据实际情况选用合适的扰流器和合适的参数。

[1] Dennis R M. Pressure vessel design manual [M]. Gulf Professional Publishing, 2004：244-245.

[2] 高文彦.化工装置中塔器的风诱导振动[J].化工设备与管 道，2001，5(38)：29-33. GAO Wen-yan. Wind induced vibration of column in chemical industry[J]. Process Equipment & Piping， 2001，5 (38)：29-33.

[3] 高鸿海, 姜锦玲. 塔振动与卡曼旋涡的解决办法[J].甘 肃科技， 2005，21(6)：35-37. GAO Hong-hai，JIANG Jin-ling. The methods for the induced vibration of towers and Kaman vortex[J].Gansu Science and Technology， 2005，21 (6)：35-37.

[4] Henry H, Bendar P E. Pressure vessel design handbook [M]. Krieger Publishing Company, 1991：107-121.

[5] 任晓蕾. 二甲苯塔振动分析[D]. 北京：北京化工大学，2008.

[6] Hiejima S, Nomura T,Kimura K, et al. Numerical study on the suppression of the vortex-induced vibration of a circular cylinder by acoustic excitation [J]. Journal of Wind Engineering and Industrial Aerodynamics,1997, 67: 325-335.

[7] Fujisawa N, Takeda G. Flow control around a circular cylinder by internal acoustic excitation[J]. Journal of Fluids and Structures, 2003,17: 903-913.

[8] Anil P, Charles H K.The instability of the shear layer separating froma bluff body [J]. Journal of Fluid Mech,1997, 333: 375-402.

[9] JB4710-2005《钢制塔式容器》[S].

Vibration suppression of towers by using new types of turbulators

TAN Wei, LI Xiao-lin, WU Hao

(Tianjin University, Tianjin 300072, China))

Acoustic turbulator and eject turbulator were designed based on the mechanics of vibration to suppress the across-wind vibration of towers.3D numerical models were set up to analyse the effect of the two new turbulators with varying parameters in wind field around the tower. It is found that under the turbulent velocity equaling to the first critical velocity and the turbulent frequency corresponding to the instability criterion of shear layer, the two new types of turbulators can get the most anti-vibration effect and the eject turbulator with the same parameters as the acoustic turbulator is proved to be more effective. The conclusions provide reference and gist to the design and application of the turbulators.

across-wind vibration; turbulator; finite element analysis; fluid-structure interaction

2013-11-08 修改稿收到日期：2014-04-10

谭蔚 女，博士，教授，1965年1月生

TH113.1；TH122

A

10.13465/j.cnki.jvs.2015.09.013