基于振源识别的高速微铣削机床状态研究

孙 岳， 于占江， 许金凯， 于化东

(长春理工大学 机电工程学院，长春 130022)

基于振源识别的高速微铣削机床状态研究

孙 岳， 于占江， 许金凯， 于化东

(长春理工大学 机电工程学院，长春 130022)

对介观尺度下三向正交的高速微铣削力混合信号提出一种有效的分离算法，从而获得高速微铣削力的真实信号及机床振动信号并基于此对机床状态进行分析。算法首先以信息量为处理标准将观测信号初步分离，再将分离得到的各分量信号作为行向量构造矩阵,最后对该矩阵进行以高斯性最大为度量的分离，逐一得到各激励源信号，并对其快速傅里叶变换得到频谱，结合机床结构及介观尺度下高速微铣削加工特点，识别微铣削力信号及机床状态信息。实验结果分析表明：该方法可成功对介观尺度下高速微铣削加工中主要激励源和机床状态进行有效识别。

高速微铣削；介观尺度；矩阵构造；信号分离；机床状态

在机械加工领域，介观尺度定义为介于宏观和微观尺度之间，几何特征尺寸在0.01 mm-1 mm之间的零件。高速微铣削作为高精度三维精密微小零件加工的一种主要方式受到越来越多的关注。而高速铣削力信号包含了丰富的微铣削加工状态信息和机床状态信息，因此对微铣削力混合信号的分析成为研究高速微铣削加工的重要途径。由于高速加工中铣削力较小，反映在信号中即为能量较弱的力信号，极易受机床部件所产生的机械噪声、环境噪声等影响。通过切削力测力计采集到的观测信号均为小信噪比的铣削力混合信号，仍然按照对常规铣削所得的大信噪比混合信号的分析方法进行分析显然是不适合的，因此对高速微铣削力混合信号进行分离是非常必要的[1-2]。

目前，盲源分离理论在信号处理中的应用已经受到极大关注。在发动机故障诊断、爆破信号分离、刀具磨损检测等领域得到广泛应用[3-6]，但将其应用在高速加工领域还鲜有人进行研究。Zhu，Hong等[7-8]利用盲源分离中的独立分量分析理论实现微铣削力混合信号去噪，为ICA应用于微铣削力混合信号分离的后续研究奠定了一定的基础。胥永刚等将盲源分离理论引入到机械设备振动信号的分离中，为机械设备的状态信息分析和故障诊断提供了新方法。赵学智等[9]先对机床主轴箱故障诊断、轴承振动信号调幅特征提取和铣削力信号处理与铣床状态信息分离进行了研究，在铣削力信号处理和机床状态信息分离方面虽然效果明显好于小波变换方法，但是由于采用的是单一铣削力信号进行分离并且未提及铣削过程中常见的高斯性噪声信号，所以激励源的识别率有待进一步提高。

实验利用本文提出的算法对测力计采集到的三向正交的微铣削力混合信号进行分离，并基于此对机床状态进行研究，证明该方法具有激励源识别率高和可同时分离非高斯信号与高斯性信号的优点。

1 实验条件

实验装置如图1所示，选用SECO905002-MEGA-T双刃立铣刀，铣刀直径0.2 mm、钝圆半径约为2.63 μm。以安装于Z向滑台上的300 W的高速电主轴驱动刀具旋转，由水平方向上的X、Y向滑台带动工件水平移动，X、Y、Z向滑台均为最小进给量2.5 μm，滑台滚珠丝杠齿距4 mm的精密滑台。实验过程中，通过安装于工件和滑台之间的Kistler9256CQ01测力计对高速微铣削力进行测量，采样频率为3 333 Hz，在X，Y，Z三向各采集了1 667个数据,并以其为对象运行算法。主轴转速40 000 r/min，进给速度30 mm/min，单齿进给量为0.375 μm/z，铣削深度为5 μm。实验流程如图2所示。

图1 实验装置Fig.1 Experimental equipment

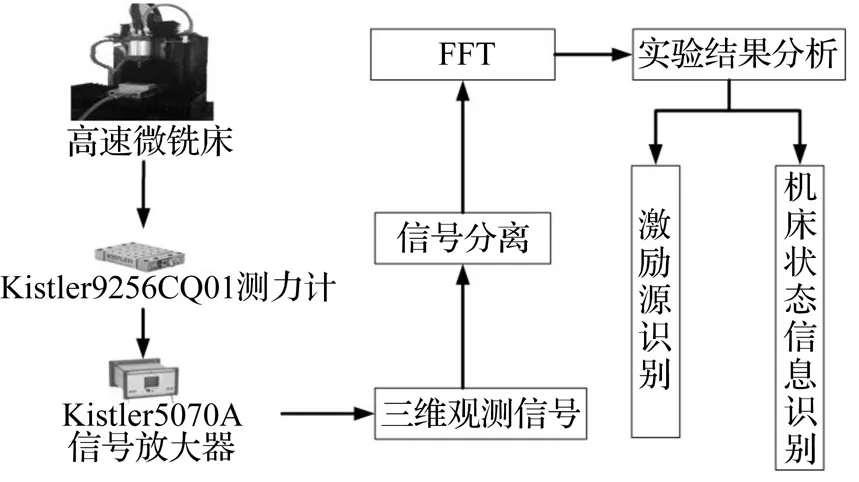
图2 微铣削力混合信号分离流程图Fig.2 Flowchart of micro-milling force mixed-signal separation

2 算法模型

根据中心极限定理，源信号的非高斯性必大于观测信号非高斯性，可通过对三维观测信号高斯性的考察来判断激励源的高斯性。为防止由于观测信号中存在多个高斯信号混叠现象引起分析偏差，首先利用式(1)峭度对不同工况下的一维观测信号X=[x(1),x(2),…,x(N)]的高斯性进行度量。

kurt(x)=k4=E{x4}-3{E{x2}}2

(1)

当随机变量为高斯分布时，其峭度值kurt(x)=0，为超高斯分布时，其峭度值kurt(x)>0，为亚高斯分布时，峭度值kurt(x)<0。

明确激励源高斯性后，利用观测信号序列X=[x(1),x(2),…,x(N)]构造算法分解对象矩阵A：试取的一系列行数m构造矩阵A，对X进行截取，每次n个点连续截取m段，并计算矩阵各奇异值σ，再根据式(2)计算各奇异值所对应的信息量，并观察信息量变化趋势，若无论在试取过程中m取何值，从某信息量ηi开始后续各信息量值均无明显变化且趋向于0，则确定矩阵A的行数m=i，列数n可由m根据式(3)求得，其中，m≥2,n≥2。构造m×n矩阵A如下：

(2)

n=int(N/m)

(3)

对于已构造的矩阵A必定存在正交矩阵U=[u1u2…um]∈Rm×m和正交矩阵V=[v1v2…vn]∈Rn×n，使得

A=USVT

(4)

其中:S=[diag(σ1,σ2,…,σp),O]或者其转置，这取决于mn，S∈Rm×n，O为零矩阵p=min(m,n)，且矩阵A的奇异值有如下关系：σ1≥σ2≥…≥σp≥0。

将式(4)写作列矢量ui和vi形式：

(5)

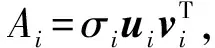
但是，高速微铣削力混合信号具有信噪比低、激励源多、耦合现象显著和可能混有高斯性信号等特点，高斯变量的熵最大。针对这些特点将s1,s2,s3，…，si(i=1,2,…,p)做进一步分离，使变换后的各信号间尽可能统计独立。

将S=[s1,s2,s3,…,sp]视为第二步分离过程中的观测向量，在第二步分离之前对其进行预处理，预处理过程如下：

①s′=s-E(s)

②s←s′

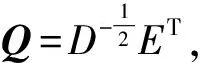
④z=Qs

⑤s←z

预处理后即进入第二步分离过程，第二步分离基本模型可表示为

s=Bd

(6)

其中:d=[d1,d2,d3,…,dq]T是q个独立信号源，S=[s1,s2,s3,…,sp]是p个混合信号，B为p×q维混合矩阵。该步算法期望得到如式(7)所示的分离矩阵W，

Ws=WBd

(7)

由式(7)可知，当W=B-1时可得到理想分离结果。具体步骤如下：

(1) 根据前面信息量分析结果，估计独立分量的个数q，令i←1;

(2) 随机选择初始化向量wi，保证‖wi‖=1;

(3) 迭代求wi：

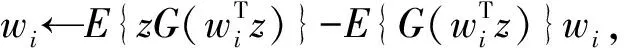
(5) 归一化处理wi：wi←wi/‖wi‖;

(6) 如果至此wi未收敛，则返回(3)。直至收敛结束。

(7) 置i←i+1，如果i≤q，返回步骤(1)。

3 实验结果

由于高速铣削信号周期极短，点数较多时不利观察时域信号，因此在对完整的1 667个点长度的信号分离之前，先截取500个数据点对混合信号时域进行观察，并对其进行傅里叶变换，其时域和频域如图3所示。

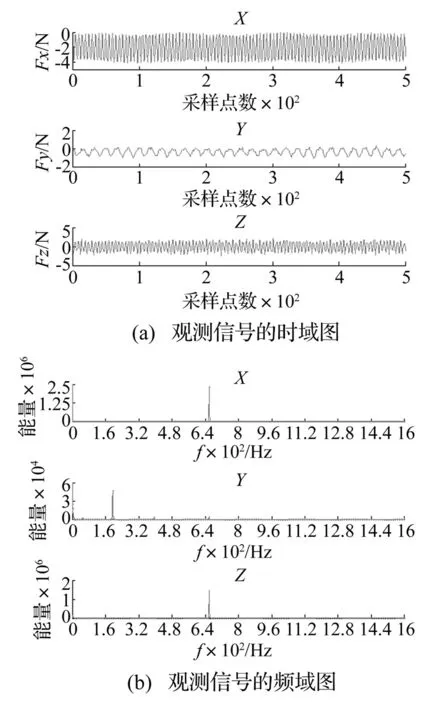
图3 测力计输出的观测信号Fig.3 The dynamometer output of observed signals

3.1 源信号高斯性与独立性判别

将如表1所示不同工况下的混合信号进行初步处理并代入式(1)，求得峭度如图4所示均大于0，说明各分量信号均具有非高斯性。而根据中心极限定理，源信号的非高斯性必大于观测信号的非高斯性，因此在此高速铣削加工中的源信号必为超高斯性信号。

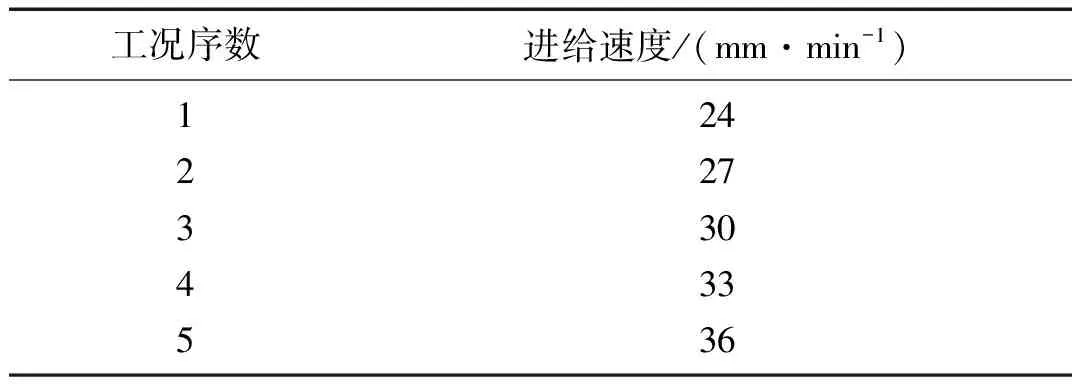
表1 工况详情

实验中，与主轴回转及滑台进给有关的激励源都具有各自的空间分布，并且有不同的传播路径和时间周期甚至特定的频率范围，因此可以近似认为各激励源之间是相互独立的。

3.2 矩阵A结构的确定

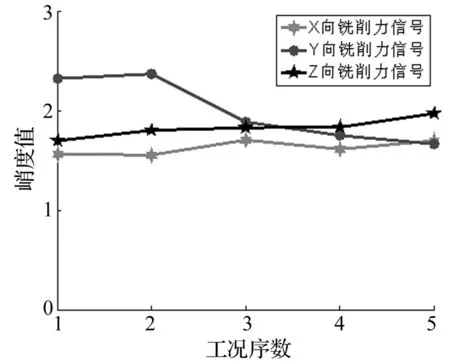
图4 五种不同工况下三向信号的峭度值Fig.4 Kurtosis of three dimensional signals under the five working conditions

算法中首先要确定X、Y、Z三向上的矩阵A(即Ax、Ay、Az)的行数，在X向分别取行数m=1,2,3,…,10。利用观测信号X=[x(1),x(2),…,x(N)]构造矩阵并对其进行奇异值分解，得到10个奇异值。再根据式(2)和式(3)可算得10个信息量S1，S2，…，S10，如图5所示，X向信号信息量在S5之后已无明显变化并基本趋于零，可见当m增大后，虽然可得到的分量信号个数增加，但信息量较大的分量信号始终只有5个。因此多余的分量信号没有考察价值。取行数m=5，X向信号的矩阵Ax结构为5×333矩阵。即将X向信号分为5个分量信号。

同理可确定，Y向信号的矩阵Ay结构为4×416矩阵。即将Y向信号分为4个分量。Z向信号的矩阵Az结构为8×208矩阵。即将Z向信号分为8个分量。

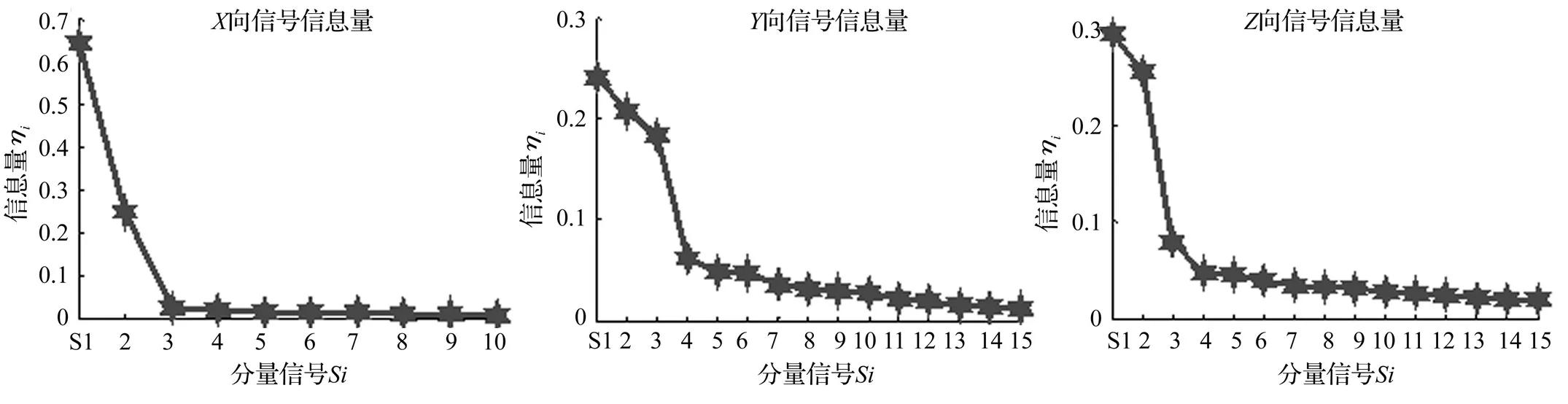
图5 三向信号信息量趋势图Fig.5 Information trend of 3-direction signals

为了在信号来源复杂的加工过程中保持对激励源的高识别率，采用控制变量法将实验设计为两阶段：第一阶段采集相同工况下只开启电主轴和同时开启电主轴与滑台进给时的信号。第二阶段采集加工中的铣削力混合信号。图6为同工况下只开启机床主轴采集到的信号的频谱。图7为同工况下同时开启机床主轴和滑台采集到的信号的频谱。图8为经本文算法分离后得到的各分量信号的频谱。

图6 机床主轴开启时x、y、z三向信号的频域图Fig.6 Frequency domain of x, y, z signals when spindle is working

图7 主轴和滑台开启时x、y、z三向信号的频域图Fig.7 Frequency domain of x, y, z signals when spindle and slipway are working

4 实验结果分析

综合考察图6、图7可见，第一阶段以只开启主轴和同时开启主轴和滑台时采集的观测信号为研究对象。只开启主轴时，X向主能量峰在667 Hz附近出现，而实验中主轴转速为40 000 r/min，其转动频率为40 000÷60=667 Hz恰好与X向能量峰所在位置吻合，由于微铣削加工中均采用精密主轴，其空转过程中振动课忽略不计，但此处采集到的信号能量值却较高。参考以往对传统铣削加工中主轴对中性不良的[10]判断，推测该铣床存在主轴对中不良情况，对本实验机床校验表明该样机确实存在此现象。对照图6、图7，同时开启主轴和滑台后在Y、Z向均捕捉到主能量在158 Hz处的信号，在未开启滑台的情况下，如图6所示，未捕捉到此频率信号，由于滑台中除运动部位螺旋副外均已紧固，因此结合实验及设备信息判断该频率处信号来自X向滑台运动过程中滚珠丝杠背隙引起的微小振动。图6、图7中，在529 Hz处均有能量峰出现，由于工件由四个角上的螺栓固定于传感器之上，工件底面与传感器存在微小间隙，主轴以40 000 r/min在封闭环境下高速旋转，极易引起工件和传感器间出现微小振动，由此判断此频率处的信号由工件和传感器间的振动引起的，此类噪声在高速加工中属于常见类型，K. ZHU等在加工过程中同样发现此类状况。

第一阶段分析表明，机床在实验工况下由于工件与传感器之间存在间隙、滑台滚珠丝杠存在背隙和主轴轴承对中误差三方面原因，产生了主能量在158 Hz、529 Hz和667 Hz的三个信号。

第二阶段分析,以实际加工中采集的X、Y、Z三向铣削力混合信号为研究对象。在0～200 Hz的较低频段内，由图8(b)可见，Y向在50 Hz处出现能量峰，考虑其能量和频率较之Y向采集到的其他分量信号均较低且属于公频频段，因此判断其为加工过程中的低频扰动成份属环境噪声范畴。由于沿X向槽铣时工件存在X、Y向的振动且X、Y向两滑台的装配结构导致X和Y方向在195 Hz附近均出现较强能量峰。沿X方向切削时Y滑台整体随动两方面原因，导致X和Y方向在195 Hz附近均出现较强能量峰。因此判断195 Hz是Y向滑台与X滑台装配间隙与加工过程中的振动现象共同引起的振动信号的主频率。

图8 算法分离结果频谱Fig.8 Spectrum result of ICA separation

在200～600 Hz频段内，图8(a)中,X3处在430～510 Hz 频段内有少量能量分布，判断为其他分量信号残余。X5分量能量集中在430～510 Hz附近，主能量峰出现在465 Hz处。在图8(b)中所有分量在400～500 Hz处均出现能量分布，Y4在320～480 Hz的频率范围有能量分布，而Y2、Y3分量在393 Hz处出现主能量峰，由此可断定Y方向上有频率在393 Hz附近的振动信号，由X、Y两方向X3、X5、Y3、Y4综合分析，判断在X、Y两个方向上捕捉到的465 Hz与392 Hz处的两个能量信号应来源于同一激励源，由于加工过程中X向滑台处于直线运动状态，丝杠副向前顶紧程度较高不易出现振动，而Y向滑台始终处于锁紧状态，丝杠副内存在间隙。因此，Y向滑台受背隙的影响大于X向滑台，根据上述实验分析可判断此频率为Y向滑台丝杠背隙所加工中引起的振动。

在600～1 000 Hz频段内，X1、X2、X3、Z1、Z6、Z8六个分量在667 Hz处均出现了能量峰，结合第一阶段分析再次验证了以667 Hz为主能量的信号为轴承对中性误差引起的振动信号。由图8(c)易见，分量Z2、Z3、Z7在860 Hz处均出现明显能量峰，且只有Z向捕捉到此处能量信号，由于主轴固定于Z向滑台上，由滚珠丝杠和步进电机控制进给和位置锁紧，因此判断为铣削过程中Z向滑台丝杠背隙引起的振动信号。

1 000～1 200 Hz频段内，只有Y、Z两个方向捕捉到信号，在Y4和图8(c)中的Z向各分量中此频段内均有能量峰出现，Z向个分量信号中此频段内的能量较强，在Z4中能量峰值较为突出。从图8(b)和图8(c)中的分布情况可判断此信号对应的激励源在Z方向上作用效果明显，由于实验中加工表面经过初加工，表面形貌特征存在一定分布规律，而Z向只有5 μm的铣削深度使得工件表面形貌对Z向作用力的影响较为明显，因此判断此频段内与铣削力信号频率接近的高频信号的出现是由于微铣削过程中切削深度受到工件表面形貌影响所引起的。

在1 200～1 600 Hz频段内，同样只有Y、Z两个方向上捕捉到信号。如图8(b)中分量信号Y4与图8(c)中分量信号Z2、Z5在1 334 Hz附近均出现能量峰，在Z3、Z4、Z7、Z8中也均有能量分布。由于主轴转动频率约为667 Hz，且使用双刃铣刀加工，因此铣削力频率应为1 334 Hz,恰好与此频率吻合，因此断定此频率信号对应的激励源为实验中的高速微铣削力。从图8(b)、(c)中可观察到，Y方向上只有Y4分量在此处有能量峰，但Y4中在50 Hz、195 Hz、860 Hz等处存在和铣削力能量相近的能量说明在Y方向采集到的铣削力信号中还混有其他激励源的能量，但是可以断定此信号即为Y向采集到的高速微铣削力信号。在Z方向上，多个分量在此处均出现能量峰，但只有Z5分量在此处出现了2.6×104的主能量，且能量值不但明显高于该分量内其他频段的能量而且在Z向其他分量中也为最大值，因此判断Z5分量即为Z向采集到的高速微铣削力信号。Z向其他分量在1334 Hz处的能量均为分离过程中残留的铣削力能量。由图8(c)可见，除分量信号Z1、Z6外图中各分量在1 530 Hz附近均有能量分布，在Z7中有较强能量，能量值约为5×104。在Z5中与1 334 Hz的铣削力信号在能量分布上具有连续性。单齿进给量和铣刀钝圆半径分别为0.187 5 μm和2.63 μm，同属微米量级。结合对介观尺度下铣削机理的研究[11-15]，分析本次实验的铣削过程中必伴随有犁切现象，在犁切过程中，切削刃划过工件表面，其表面发生弹塑性变形，因此判断此频率处能量信号由微铣削过程中的犁切现象所引起。

经过第一、二阶段分析，成功分离出1 334 Hz的高速微铣削力信号。并且通过对信号频率特点的考察，识别出各频段内对应的激励源，如50 Hz左右的环境噪声信号和包括滑台背隙、装配间隙等原因引起的多个机械噪声，明确了实验工况下存的机床状态信息，为机床进一步优化提供有力依据。

5 结 论

(1) 针对介观尺度下高速铣削加工中的小信噪比铣削力混合信号，提出了一种将奇异值分解和独立分量分析相结合的算法，该算法能有效地分离高速微铣削力信号及设备中各结构间产生的振动信号。

(2) 基于算法分离结果，结合介观尺度下微铣削加工特点、微切削机理及实验用微铣床结构特点，识别出各频段内的激励源及频率范围。

(3) 该方法可成功识别铣削力信号的同时保证分离结果中各振动信号无相位偏移现象。

[1] Zhu K, Hong G S，Wong Y S，et al. Cutting force denoising in micro-milling[J].International Journal of Production Research, 15 August,2008,46(16):4391-4408.

[2] Shao Hua, Shi Xin-hua, Li Lin. Power signal separation in milling process based on wavelet transform and independent component analysis[J]. International Journal of Machine Tools & Manufacture, 2011, 51: 701-710.

[3] Pöyhönen S, Jover P, Hyötyniemi H. Independent component analysis of vibrations for fault diagnosis of an induction motor[C]. International Conference Circuits, Signals and Systems, Mexico. 2003, 1: 203-208.

[4] Lin J, Zhang A. Fault feature separation using wavelet-ICA filter[J]. NDT & E International, 2005, 38(6): 421-427.

[5] Gelle G, Colas M, Serviere C. Blind source separation: a tool for rotating machine monitoring by vibrations analysis[J]. Journal of Sound and Vibration, 2001, 248(5): 865-885.

[6] 李欣，梅德庆，陈子辰. 基于ICA的镗削过程颤振征兆信号分离方法研究[J]. 振动与冲击, 2013,32(9):5-9. LI Xin, MEI De-qing, CHEN Zi-chen. ICA based separation of chatter symptom signals for precision hole boring processing[J]. Journal of Vibration and Shock, 2013,32(9):5-9.

[7] 胥永刚，张发启，何正嘉. 独立分量分析及其在故障诊断中的应用[J]. 振动与冲击, 2004, 23(2): 104-107. XU Yong-gang, ZHANG Fa-qi, HE Zheng-jia. Independent component analysis and its applications to fault diagnosis [J]. Journal of Vibration and Shock, 2004, 23(2): 104-107.

[8] 杨杰，郑海起，田昊，等. 基于独立分量分析的欠定盲源分离方法[J]. 振动与冲击, 2013, 32(7): 30-33. YANG Jie, ZHENG Hai-qi, TIAN Hao, et al. Underdetermined bind source separation method based on independent component analysis[J]. Journal of Vibration and Shock, 2013, 32(7): 30-33.

[9] 赵学智，叶邦彦，陈统坚.奇异值差分谱理论及其在车床主轴箱故障诊断中的应用[J]. 机械工程学报，2010, 46(1)：100-108. ZHAO Xue-zhi, YE Bang-yan, CHEN Tong-jian. Difference spectrum theory of singular value and its application to the fault diagnosis of headstock of lathe [J]. Journal of Mechanical Engineering, 2010, 46(1)：100-108.

[10] 赵学智，陈统坚，叶邦彦. 基于奇异值分解的铣削力信号处理与铣床状态信息分离[J]. 机械工程学报, 2007, 43(6): 169-174. ZHAO Xue-zhi, CHEN Tong-jian, YE Bang-yan.Processing of milling force signaland isolation of state information of milling machine based on singular value decomposition[J]. Chinses Journal of Mechanical Engineering, 2007, 43(6): 169-174.

[11] 李晓舟，于化东，许金凯，等. 微切削加工中切削力的理论与实验[J]. 光学精密工程, 2009,17(5): 1086-1092. LI Xiao-zhou,YU Hua-dong,XU Jin-kai,et al. Theory and experiments of cutting forces in micro-cutting process[J]. Optics and Precision Engineering, 2009,17(5): 1086-1092.

[12] Vakondios D, Kyratsis P, Yaldiz S, et al. Influence of milling strategy on the surface roughness in ball end milling of the aluminum alloy Al7075-T6[J]. Measurement, 2012,45:1480-1488.

[13] Sun Yue, Liu Yong-sheng,Yu Zhan-jiang, et al. Milling force mixed-signal denoising based on ICA in high speed micro-milling[C]. IEEE International Conference on Robotics and Biomimetics (ROBIO), Guangzhou, China: IEEE. 2012: 1023-1028.

[14] 李一全，孙岳，董山恒，等. 基于独立分量分析的高速微铣削力混合信号噪声分离方法[J]. 中国测试，2013,39(2)：6-13. LI Yi-quan, SUN Yue, DONG Shan-heng, et al. Milling force mixed-signal denoising based on ICA in high speed micro-milling[J]. China Measurement & Test, 2013,39(2)：6-13.

[15] 李成峰，来新民，李洪涛，等. 介观尺度铣削工艺分析[J]. 农业机械学报, 2008, 39(1): 156-164. LI Cheng-feng, LAI Xin-min, LI Hong-tao, et al. Technology analysis on mesoscale milling[J]. Transactions of the Chinese Society for Agricultural Machinery, 2018,39(1)：156-164.

High speed micro milling machine condition monitoring based on vibration source identification

SUN Yue, YU Zhan-jiang, XU Jin-kai, YU Hua-dong

(Department of Mechanical and Electric Engineering, Changchun University of Science and Technology, Changchun 130022, China)

An algorithm was proposed for effectively seperating the mixed-signal of three directional high speed micro milling force in mesoscale. The real high speed micro milling force signals and machine vibration signals were then obtained. Based on the algorithm, machine conditions were analyzed. Taking information content as the processing standard, the mixed-signals were separated preliminarily to get the component signals. As row vectors, the component signals obtained were then used to build a matrix. The matrix was further separated according to the rule of most Gaussian. The exciting source signals were sequentially separated out one by one. The results were processed by FFT and transormed to spectrums. Considering the features of high speed micro milling machining in mesoscale, micro milling force signals and conditions of machine were identified. The experiment results show that the algorithm can successfully indentify the main exciting sources and machine conditions during mesoscale high speed micro milling.

high speed micro milling; meso scale; matrix creation; signal separation; machine condition

国家自然科学基金(51275056)

2013-05-03 修改稿收到日期：2014-04-30

孙岳 男，硕士，1986年6月生

于化东 男，博士，教授，博士生导师，1961年生

TH911.7

A

10.13465/j.cnki.jvs.2015.09.012