基于改进函数替换法的变形无人机LPV系统建模
吴成富, 邵朋院
(西北工业大学 无人机特种技术国家重点实验室, 陕西 西安 710065)
基于改进函数替换法的变形无人机LPV系统建模
吴成富, 邵朋院
(西北工业大学 无人机特种技术国家重点实验室, 陕西 西安 710065)
为了提高函数替换法的适用范围,对现有的函数替换法进行了分析,提出了一种改进的函数替换法,并使用该方法建立了变形无人机的纵向LPV模型。首先,对现有的LPV系统建模方法进行了总结,通过在函数替换法基础上引入部分线性化,使变参数的选取更为灵活,增强了函数替换法的实用性;然后,以变形无人机纵向系统为例,给出了基于所提出方法的纵向LPV系统模型;最后,对所建立模型的有效性进行了验证。结果表明,所建立的模型与原始非线性模型近似程度很高,证明了该方法的有效性。
LPV系统; 系统建模; 变形无人机; 函数替换法
0 引言
在控制工程中,多数系统均为非线性、时变且不确定的,如本文研究的变形无人机(MUAV)。虽然在理论上非线性控制、鲁棒控制和自适应控制等先进控制方法可以解决上述问题,但是在工程实际中这些方法常常难以应用。在工程实际中,应用最多的仍然是基于线性定常(LTI)系统模型的PID控制[1]。在处理非线性、时变特性和不确定性时,工程中常用的方法是增益调度PID方法[2]。这种增益调度方法虽然可以处理很多实际的非线性参变系统的控制问题,但其理论基础仍然是基于LTI系统的线性控制理论,所以无法从理论上保证被控系统在整个运行包线范围内的鲁棒性和稳定性。
针对此问题,Rugh和Shamma[3]提出了线性变参数系统(Linear Parameter Varying, LPV),该系统具有LTI系统的形式,并引入了变参数。理论研究表明,非线性系统都可以转化为LPV系统来研究其控制问题;由于形式相同,可以将对于LTI系统的研究结论拓展到LPV系统。因此,LPV系统的概念一经提出,便成为控制学界一个新的研究热点。
模型建立是控制的基础,系统建模也成为LPV系统控制研究的一个重要问题。与其他系统类似,LPV系统的建模方法也可以分为机理建模和系统辨识两类。由于飞行力学的发展,对于飞机的气动力学和运动学机理已经具有较为深入的认识,本文主要研究机理建模方法,即得到非线性模型之后,如何将其转化成LPV系统模型。在总结现有LPV系统建模方法的基础上,提出了一种改进的函数替换方法,并在MUAV的LPV建模中进行应用,证明了该方法的有效性。
1 一种改进的LPV系统建模方法
1.1 LPV系统的定义
LPV系统是指具有线性系统的形式,而系统中某些参数随着外部参数的变化而变化的系统。用状态空间形式表达如下:

(1)
式中:x,u,y分别为系统状态、控制输入和量测输出;θ为变参数向量,即θ=[θ1,θ2,…,θn]T。对于LPV系统,要求所有变参数是可测的;同时,对于实际系统,假设变参数及其变化率有界。
1.2 改进的函数替换法
本文中的LPV系统建模特指将非线性模型转化为LPV系统模型。即将如下系统转化为系统式(1)的形式:
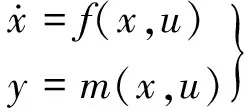
(2)
在现有文献中,LPV系统的建模方法一般有如下几种:雅克比线性化方法[4]、状态变换法[5]、基于速度的线性化方法[6]和函数替换法[5]。由于采用函数替换法进行LPV建模时必须将所有与非线性有关的状态纳入变参数,若非线性相关的状态不可测量,则函数替换法无法应用。改进方法的核心思想是将与非线性有关的状态中不能或不需要纳入的变参数进行线性化。
下面进行详细说明。为简明起见,只对状态方程进行函数替换,输出方程类似,在此不再赘述。
对系统式(2),设x=[x1,x2,x3]T,其中x1和x2为与非线性有关的状态,x3为与非线性无关的状态。
则系统式(2)中的状态方程可以写成:
(3)
若使用原始的函数替换法,则需要将x1和x2均纳入变参数,若x1不可测或者得到的变参数过多,则需要将x1从变参数向量中剔除,本小节通过对x1进行线性化,从而将x1从变参数向量中剔除。
选取参考点x0=[x10,x20,x30]T,定义新状态变量dx1=x1-x10,并在该参考点处对x1进行线性化。定义辅助函数:
(4)
则有:
(5)
上式中与x2无关的非线性项只有
(6)
再定义dx3=x3-x30,将x3线性化并省略一阶小量的乘积项,则有:
Δgx3=g(x10,x2)x30+g(x10,x2)dx3+
(7)
若对x1线性化之后无与x3有关的乘积项,则对x3线性化的步骤可以省略。非线性项剩下与x2有关的项,对这些项进行函数替换,即可得到变参数只包含x2的LPV系统。
2 在变形无人机建模中的应用
本文研究对象为Z型折叠翼变形无人机,其机翼分内外两段,内段机翼可以绕旋转轴转动,在内段机翼转动时,外段机翼始终保持水平,如图1所示。

图1 变形无人机展开和折叠构型Fig.1 Expanding and folding configurations of MUAV
下面使用改进的函数替换法来建立变形无人机的LPV模型。为简明起见,只建立其纵向系统模型。飞机的六自由度方程见文献[7],结合方向余弦矩阵,可以分离出纵向运动方程为:
(8)
式中:u,w分别为机体轴Ox和Oz轴方向的速度分量;q为机身俯仰角速率;θ为俯仰角;M为俯仰力矩;Iyy为绕机体轴Oy轴的转动惯量;Fx和Fz分别为合外力沿机体Ox和Oz轴的分量,如下式所示:
(9)
式中:T,L,D分别为飞机的发动机推力、升力和阻力,L和D的组成和计算参见文献[7]。假设发动机推力线过重心,且发动机安装角为0°。
设飞机的气动系数和导数可以表示为C*=f*(v1,v2,…),其中“*”表示气动力或力矩;v1,v2,…表示查表的索引项。例如升力对升降舵的导数表示为:
CLδe=fLδe(α,θr,δe)
通过观察气动系数可以发现,飞机的舵偏输入以及油门输入与输出的力和力矩近似呈线性关系,所以,可以将输入进行线性化。例如,对于升降舵,可以近似认为下式成立:
f*(α,θr,δe)=f*(α,θr)δe
其他控制的处理方法类似,处理之后所有的气动系数和气动导数均可以表示成α和θr的函数,联立以上各式,可以得到:
(10)
式中:Q为动压;Sw为机翼参考面积。为简明起见,在表达式中将气动系数中的变参数项α和θr省略。
非线性项中包含了速度分量u和w,迎角α,折叠角θr,俯仰角θ和马赫数Ma。可以看出,非线性项与θ的非线性关系最为简单,仅有sinθ和cosθ两项,所以用对θ的线性化来说明如何通过部分线性化来减少必须包含的变参数个数。
选取参考点θ0,对三角函数进行线性化,如下式所示:
(11)
将式(11)代入式(10),并定义dθ=θ-θ0,可得:
(12)
选取状态变量为x=[u,w,q,dθ]T,输入为u=[δe,δT]T,则可以将式(12)表示成如下的状态空间形式:
(13)
其中,系统A和B矩阵中各项分别为:
(14)
非线性项h中的各项为:
hu=m-1QSw(fCLcosα-fCDsinα)-gsinθ0
(15)
hw=gcosθ0-m-1QSw(fCLsinα+fCDcosα)
(16)
(17)
以上讨论中,变参数中的机体轴速度分量u,w是不能直接测量的,在无风假设下,这两个量与飞机的空速V和迎角α是等价的,有如下关系成立:
(18)
在飞机飞行高度变化不大的前提下,Ma和V也是对应的,所以,式(12)中的LPV系统的变参数向量可以选取为θ=[V,α,θr]T。对于查表的非线性关系,例如气动系数,可以采用多项式拟合获得其解析形式,多项式的形式可以通过观察气动数据曲线获得。
以Cmq为例,通过观察气动系数曲线,可以看出其与α近似呈三次多项式关系,与θr近似呈四次多项式关系,故采用如下多项式形式:
fCmq(α,θr)=a0+a1α+a2α2+a3α3+
(19)
使用吹风数据进行拟合,得到各个系数值:a0=-8.605 9,a1=-0.212 6,a2=-15.839 7,a3=52.424 9,b1=2.890 7,b2=-3.833 4,b3=2.416 7,b4=-0.525 3。将结果代入式(19),在吹风数据点处由下式求出拟合值和实际吹风值的相对误差:
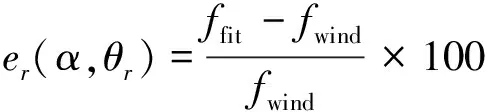
(20)
式中:ffit为拟合数据;fwind为吹风数据。
计算结果如图2所示。由图可知,拟合结果的最大误差不超过1.5%,拟合误差较小,在工程容许的误差之内。
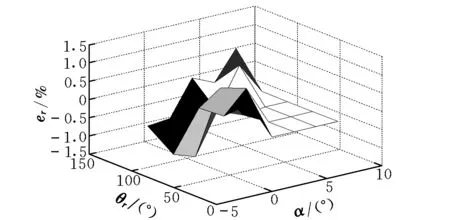
图2 拟合数据和吹风数据相对误差曲线Fig.2 Relative error between fitted data and wind-tunnel data
将拟合结果代入式(12),即可得到解析形式的LPV模型。
3 仿真结果及分析
将建立的LPV模型与原始非线性模型响应进行对比,给定初始状态为空速25 m/s,折叠角θr为0°的配平状态,在仿真进行2 s时,机翼以20 (°)/s的速率进行折叠,到8 s时折叠角达到120°,之后保持2 s,得到各个量的响应如图3~图5所示。

图3 俯仰角响应曲线Fig.3 Responses of angle of pitch

图4 迎角响应曲线Fig.4 Responses of AOA
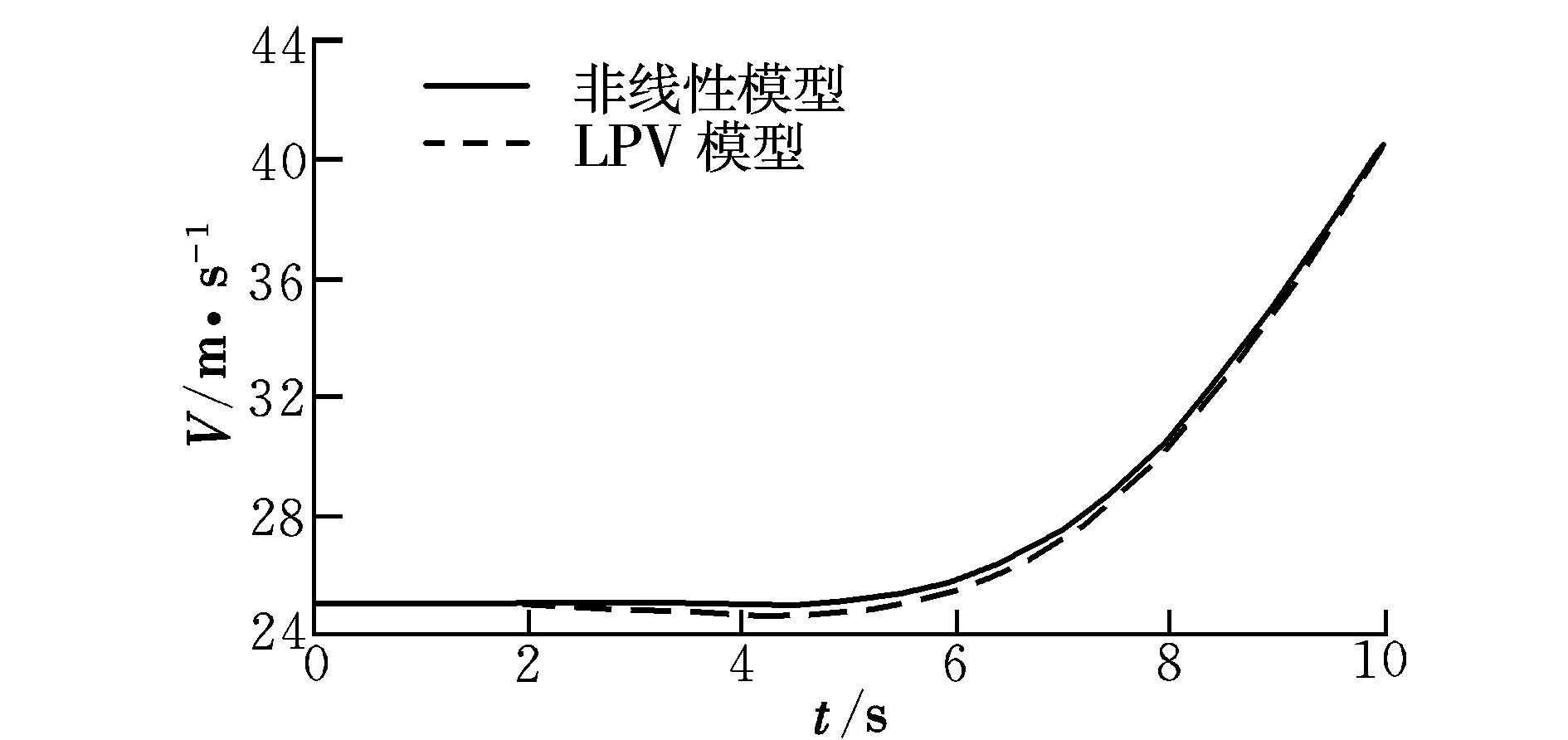
图5 空速响应曲线Fig.5 Responses of airspeed
由图3~图5可以看出,所建立的LPV模型与原始非线性模型响应十分接近,迎角和俯仰角的响应误差均小于0.5°,空速响应误差小于1 m/s,所以文中提出的建模方法是可行的。如果减小线性化区间间隔,则建模误差可以进一步减小。
4 结束语
针对函数替换法不能自由选取变参数的缺点,通过引入部分线性化对其进行改进,使用改进方法建立了变形无人机的纵向LPV系统模型。与原有的函数替换法相比,该方法的优点在于可以自由选取变参数,从而增强了函数替换法的应用范围。
由于引入了线性化,该方法与原有的函数替换法相比存在一定的建模误差,虽然建模误差可以通过增加线性化的网格密度来减小,但是网格密度的选取尚无理论方法可用,只能依据实际的对象,按照经验选取,这是该方法需要进一步研究的问题。
[1] Ang K H,Chong G,Li Y.PID control system analysis,design,and technology[J].Control Systems Technology,IEEE Transactions on,2005,13(4):559-576.
[2] Shamma J S,Athans M.Analysis of gain scheduled control for nonlinear plants[J].Automatic Control,IEEE Transactions on,1990,35(8):898-907.
[3] Rugh W J,Shamma J S.Research on gain scheduling[J].Automatica,2000,36(10):1401-1425.
[4] Shin J Y.Quasi-linear parameter varying representation of general aircraft dynamics over non-trim region[R].NASA/CR-2007-213926,2007.
[5] 李文强.LPV系统鲁棒变增益控制研究及其应用[D].长沙:国防科学技术大学,2009.
[6] 王青,王通,后德龙,等.基于速度线性化的变体飞行器鲁棒变增益控制[J].系统工程与电子技术,2014,36(6):1130-1136.
[7] 吴森堂,费玉华.飞行控制系统[M].北京:北京航空航天大学出版社,2005:58-59.
(编辑:任亚超)
LPV modeling of morphing UAV based on improved function-substitution method
WU Cheng-fu, SHAO Peng-yuan
(National Key Laboratory of Special Technology on UAV, NWPU, Xi’an 710065, China)
To enhance the applicability of function-substitution method, an improved function-substitution based modeling method for LPV systems is proposed and applied on modeling of the longitudinal system of morphing UAV. Partial linearization is introduced to function-substitution method, thus the varying parameters can be chosen more flexibly and the number of varying parameters can be reduced. After that, the LPV model for longitudinal system of morphing UAV is derived using the proposed method and the simulation result shows that the responses of LPV model is highly consistent with the nonlinear model.
LPV system; system modeling; morphing UAV; function-substitution method
2015-01-15;
2015-05-18;
时间:2015-09-25 16:10
吴成富(1962-),男,浙江金华人,教授,博士生导师,主要研究方向为无人机导航、制导与控制; 邵朋院(1986-),男,陕西咸阳人,博士研究生,主要研究方向为无人机导航、制导与控制。
V279
A
1002-0853(2015)06-0565-04

