基于非线性增益的高超声速飞行器非线性控制

梁帅, 孙秀霞, 刘树光, 刘希, 唐强

(1.空军工程大学 航空航天工程学院, 陕西 西安 710038;2.西安飞行自动控制研究所 飞行器控制一体化技术重点实验室, 陕西 西安 710065)

基于非线性增益的高超声速飞行器非线性控制

梁帅1, 孙秀霞1, 刘树光1, 刘希1, 唐强2

(1.空军工程大学 航空航天工程学院, 陕西 西安 710038;2.西安飞行自动控制研究所 飞行器控制一体化技术重点实验室, 陕西 西安 710065)

针对高超声速飞行器纵向模型,考虑参数摄动、未建模动态和外界干扰等各种不确定性因素的综合影响,提出了一种基于非线性增益的递归滑模动态面控制方案。该方案通过非线性增益函数调节高超声速飞行器姿态控制精度与控制增益之间的矛盾,利用神经网络逼近飞行器气动参数不确定性和未知外界干扰,进一步通过设计递归滑模动态面控制器提高系统的控制精度。仿真结果表明,所提控制方案不仅提高了飞行器的控制精度,而且对模型不确定性和外界干扰具有较强的鲁棒性。

高超声速飞行器; 非线性增益; 递归滑模动态面控制; 神经网络

0 引言

高超声速飞行器以其飞行速度快、打击范围广、机动作战能力强等显著特点在全球实时侦查和远程精确打击等方面具有广阔的应用前景,已经成为各发达国家飞行器发展的热点[1]。高超声速飞行器由于其特殊的飞行环境以及复杂的动力学特征,使得其飞行控制面临多变量、强耦合、强非线性等控制难题[1-2]。

针对高超声速飞行器复杂的控制问题,很多学者提出了诸如反步控制[3]、动态面控制[4]以及自适应动态逆控制[5]等控制方法,很好地解决了高超声速飞行器巡航飞行过程中的跟踪控制问题。对于含有不确定因素的飞行器模型,文献[6-9]分别采用鲁棒控制、自适应滑模控制、自适应神经网络动态面控制以及基于滑模的鲁棒控制等方法,均取得了一定的控制效果。但当增大控制增益进一步提高姿态控制精度时,这些方法却难以克服控制精度与控制增益之间的矛盾。

基于上述分析,本文结合非线性增益函数[10]提出一种基于非线性增益的递归滑模动态面控制方法,并与经典的神经网络动态面方法[11]进行对比。具体方案为:(1)在高度控制器的每一步设计中引入递归滑模面,使控制律的设计综合考虑前面每个子系统跟踪误差间的相互影响;(2)通过非线性增益函数,调节高超声速飞行器姿态控制精度与控制增益之间的矛盾;(3)改进神经网络的逼近方式,提高系统精度;(4)基于Lyapunov稳定性定理,证明纵向控制系统的半全局稳定性,并保证闭环系统所有信号一致,最终有界。通过仿真验证,表明所提的控制方案不仅具有良好的控制精度,而且对模型不确定性和外界干扰具有较强的鲁棒性。

1 问题描述

本文采用美国NASA Langley研究中心给出的高超声速飞行器纵向模型以及发动机模型,具体参见文献[1,12]。

2 控制器设计

假设1:由于迎角α较小,以致于使得推力项远小于升力项,故而可以忽略推力项的影响。

通过上述假设可以把纵向通道分成两个子系统分别进行控制器设计。其中,高度子系统中用航迹倾角γd来代替高度指令Hd作为系统的指令信号。

(1)

式中:kP>0为常数。

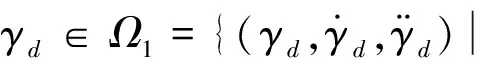
假设4:神经网络跟踪误差‖ξi‖≤ρi，且ρi有界。

2.1 高度控制器设计

为便于系统控制律设计,将纵向模型转换为严反馈形式。模型中俯仰角θ=α+γ,取状态变量x=[x1,x2,x3],其中:x1=γ,x2=θ,x3=q,高度控制量u=δe。高度严反馈形式如下[13]:

(2)

假设5:根据式(2),存在正常数gm和gM,使得gm≤gi≤gM且gi(i=1,2,3)≥0成立。

步骤1:定义第一个滑模面:

e1=x1-γd,s1=e1

(3)

对式(3)求导得:

(4)

由于ψ1未知,利用RBF神经网络[10]进行逼近,设计虚拟控制律和自适应律:

(5)

式中:L1(s1)的意义以及表达式参见文献[10]。

为避免在下一步对虚拟控制律求导,采用动态面控制技术即引入一阶低通滤波器进行滤波:

(6)

步骤2:定义第二个递归滑模面：

e2=x2-z2,s2=c1s1+e2

(7)

对式(7)求导可得:

(8)

(9)

设计虚拟控制律和自适应律:

(10)

同样,设计一阶低通滤波器:

(11)

步骤3:定义第三个递归滑模面:

e3=x3-z3,s3=c2s2+e3

(12)

同步骤2可得出最终控制律和自适应律:

(13)

注1:从式(5)、式(10)和式(13)可以看出,在控制器每步设计时都引入了非线性增益函数,有效地改善了控制增益和控制精度之间的矛盾。

注2:在设计虚拟控制律和控制律过程中,采用递归滑模的方式对上一步产生的误差进行削弱。

注3:神经网络逼近过程中采取逼近递归整体项如式(9),进一步减小了神经网络的逼近误差。

2.2 速度控制器设计

速度模型同样化成严反馈形式[13]:

(14)

定义速度滑模面:

sv=ev=V-Vd

(15)

控制律以及自适应律的设计同高度控制器设计,即:

(16)

3 稳定性分析

3.1 高度稳定性分析

定义滤波误差为:

yi=zi-xid(i=1，2,3)

(17)

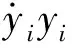
(18)

定理1:考虑由高超声速模型[1,12]以及控制律和自适应律构成的闭环系统,当假设1～5成立且系统初始状态有界时,则存在一定控制参数使得闭环系统所有状态半全局一致最终有界。

证明:定义第一个Lyapunov函数:

(19)

由Young’s不等式,对于i=1,2,3,有:

(20)

(21)

对式(19)求导,把式(5)、式(20)以及式(21)代入并进行缩放得:

(22)

定义第二个、第三个Lyapunov函数:

(23)

类似地,可以得出:

(24)

高度Lyapunov函数为:

V=V1+V2+V3

(25)

对其求导,且把式(22)和式(24)代入并进行缩放得:

(26)

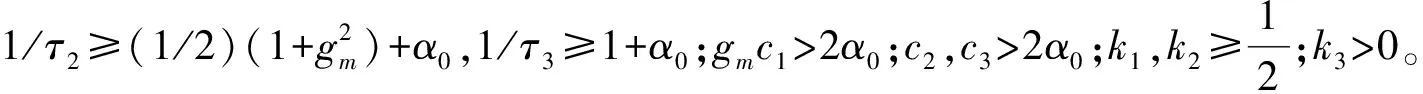
(27)

定义:

因此,式(27)可以化简为:

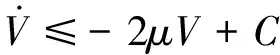
(28)

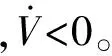
3.2 速度稳定性分析

定义速度Lyapunov函数:

(29)

对式(29)求导,把控制律以及自适应律代入后进行缩放,最终可以得到:

(30)

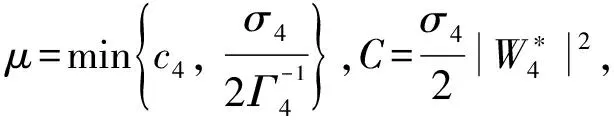
4 数值仿真结果及分析

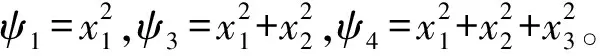
控制器参数设置:首先采取小增益进行仿真。两种方法采取同样的控制参数,即:k1=4,k2=4,k3=2,c4=4,τ2=τ3=0.01,kp=1,Γ1=Γ2=Γ3=Γ4=diag{5};神经网络节点均选为n=10,中心值ζi在区间[-2,2]均匀取值，ηi=0.1,σi=10-3;本文其他参数a1=a2=a3=0.5,b1=b2=b3=1,δ1=δ2=δ3=10-9,c1=1,c2=2,c3=2。仿真结果如图1和图2所示。

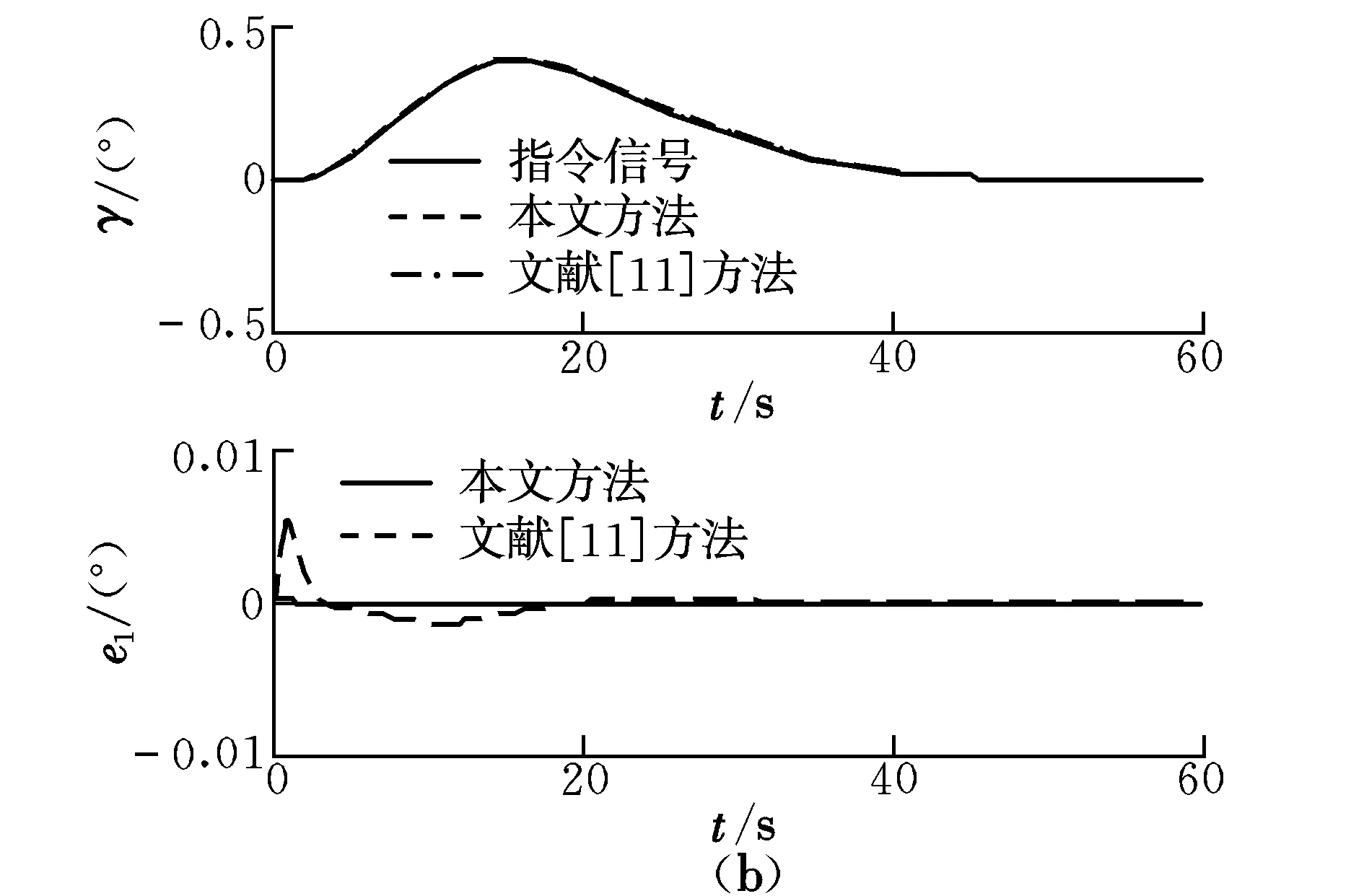
图1 小增益下的高度控制效果对比Fig.1 Comparison of height control effects under low gain

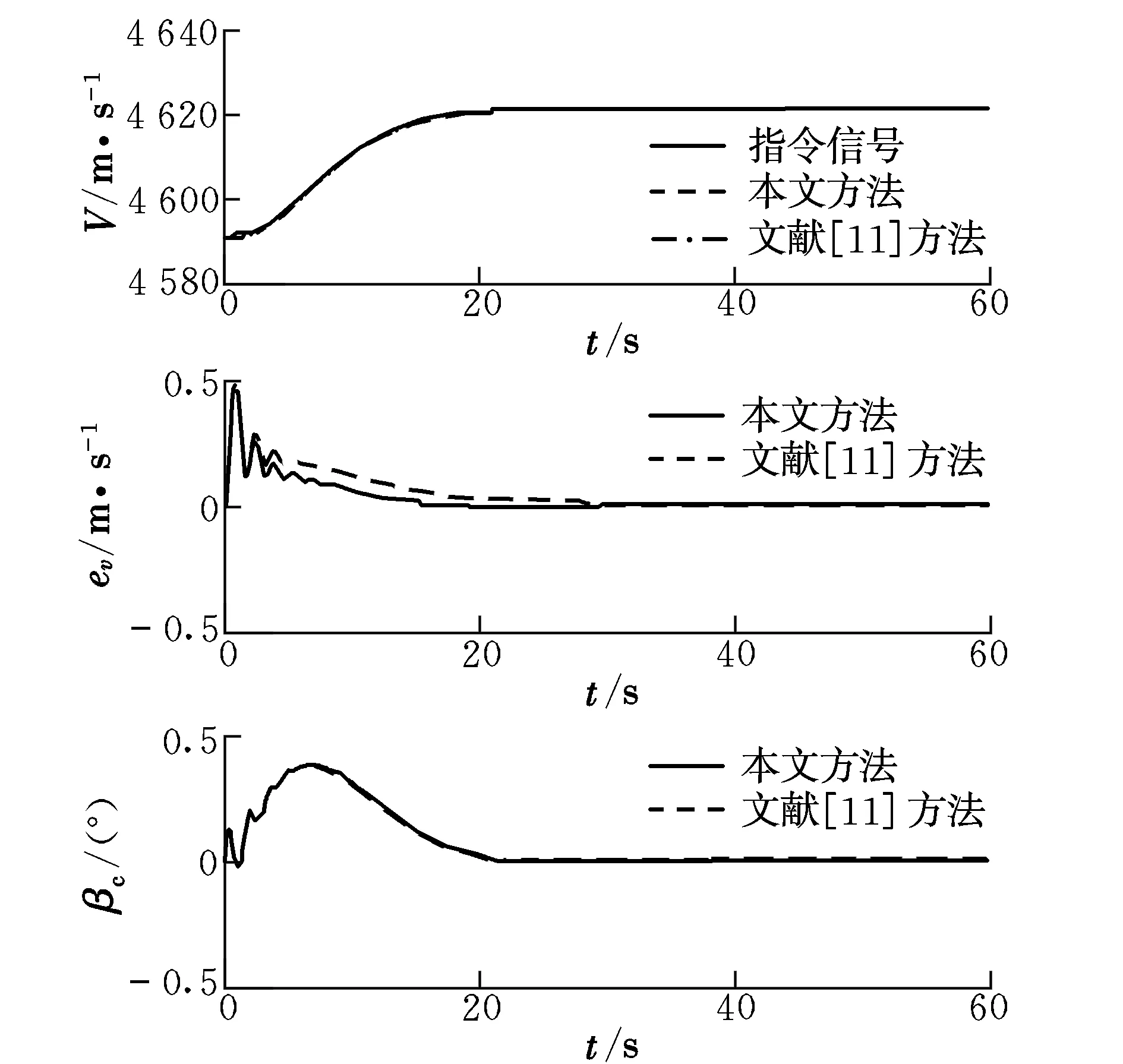
图2 小增益下的速度控制效果对比Fig.2 Comparison of velocity control effects under low gain

然后,采用较大增益进行仿真,控制器参数k1=40,k2=40,其他参数保持不变。仿真结果如图3和图4所示。

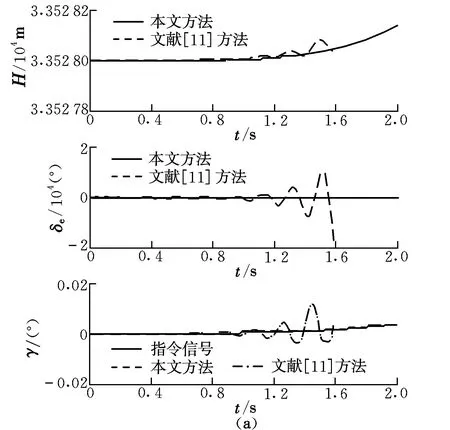
图3 大增益下的高度控制效果对比图Fig.3 Comparison of height control effects under high gain

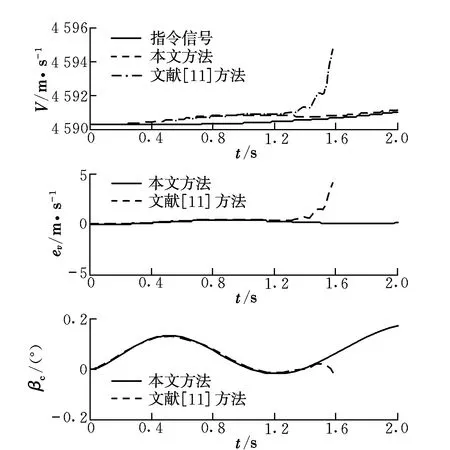
图4 大增益下的速度控制效果对比Fig.4 Comparison of velocity control effects under high gain

对于存在不确定性的高超模型,根据图1和图2可以发现,当控制增益较小时,采用本文方法与文献[11]方法都可以达到比较好的跟踪效果,但采用本文方法得到的计算结果误差相对较小;当增大控制增益时,由图3和图4可以看出,采用本文方法仍然能够保持较好的控制效果,而采用传统方法在1.5 s时就发散了。

5 结束语

本文针对存在参数不确定性以及非线性干扰的高超声速飞行器,设计了非线性增益的递归滑模动态面控制方案。该方案通过神经网络逼近未知非线性函数,利用递归滑模解决动态面控制中滤波器时间常数变化导致的控制性能下降问题,同时设计非线性增益函数,解决了大增益与控制精度之间的矛盾。仿真结果表明,所设计的控制方案能够有效克服参数不确定等因素带来的干扰,提高了系统的鲁棒性,使飞行器以较高的控制精度稳定飞行。同时,该方案由于设计简单、易于实现,具有一定的工程实用价值。

[1] 张强,吴庆宪,姜长生,等.近空间飞行器鲁棒自适应 Backstepping 控制[J].系统工程与电子技术,2012,34(4):754-760.

[2] Jason T Parker,Andrea Serrani,Stephen Yurkovich,et al.Control-oriented modeling of an air-breathing hypersonic vehicle [J].Journal of Guidance,Control,and Dynamics,2007,30(3):856-869.

[3] 刘燕斌,陆宇平.基于反步法的高超音速飞机纵向逆飞行控制[J].控制与决策,2007,22(3):313-317.

[4] 程志浩,孙秀霞,刘树光,等.高超声速飞行器自适应神经网络动态面控制[J].飞行力学,2013,31(5):425-428.

[5] 遆晓光,孔庆霞,余颖.基于自适应动态逆的高超声速飞行器姿态复合控制[J].宇航学报,2013,34(7):955-962.

[6] Lisa Fiorentini,Andrea Serrani.Nonlinear robust adaptive control of flexible air-breathing hypersonic vehicles[J].Journal of Guidance,Control,and Dynamics,2009,32(2):401-416.

[7] Hu Xiaoxiang,Wu Ligang,Hu Changhua,et al.Adaptive sliding mode tracking control for a flexible air-breathing hypersonic vehicle[J].Journal of the Franklin Institute,2012,349(2):559-577.

[8] 张天平,施袅锨,沈启坤.具有未建模动态的自适应神经网络动态面控制[J].控制理论与应用,2013,30(4):475-481.

[9] Hu Zhubing,Mo bo,Zhou Dezhi,et al.Robust nonlinear control of a hypersonic aircraft based on sliding mode control[J].Procedia Engineering,2012,29(3):837-842.

[10] 刘希,孙秀霞,刘树光,等.非线性增益递归滑模动态面自适应NN控制[J].自动化学报,2014,40(10):2193-2202.

[11] Wang Dan,Huang Jie.Neural network-based adaptive dynamic surface control for a class of uncertain nonlinear systems in strict-feedback form[J].IEEE Transactions on Neural Networks,2005,16(1):195-202.

[12] Xu H J,Mirmirani M,Ioannou P A.Robust neural adaptive control of a hypersonic aircraft [C]//AIAA Guidance,Navigation,and Control Conference and Exhibit.Austin,USA,2003:1-8.

[13] 后德龙,王青,董朝阳,等.高超声速飞行器抗干扰反步滑模控制[J].北京航空航天大学学报,2014,40(1):80-85.

(编辑：姚妙慧)

Nonlinear control based on nonlinear gain of hypersonic vehicle

LIANG Shuai1, SUN Xiu-xia1, LIU Shu-guang1, LIU Xi1, TANG Qiang2

(1.Aeronautics and Astronautics Engineering College, AFEU, Xi’an 710038, China;2.Key Laboratory of Integrated Aircraft Control, Xi’an Flight Automatic Control Research Institute, Xi’an 710065, China)

Considering the combined effect of various uncertain factors, such as parameter perturbation, unmodeled dynamics and external disturbances, a recursive sliding mode dynamic surface control is based on nonlinear gain for hypersonic vehicle longitudinal model. The solution is to adjust the contradiction between the hypersonic vehicle attitude control accuracy and control gain by nonlinear gain, using neural network to approximate aerodynamic parameter uncertainty and unknown disturbance so as to further improve the control precision of the system through designing recursive sliding dynamic surface controller. The simulation results show that the proposed control scheme can not only improve the control precision of the aircraft, but also have stronger robustness for model uncertainty and external disturbance.

hypersonic aircraft; nonlinear gain; sliding mode dynamic surface control; neural network

2015-03-26;

2015-07-09;

时间:2015-08-17 11:04

航空科学基金资助(20135896025)

梁帅(1990-)，男，安徽亳州人，硕士研究生，主要研究方向为飞行控制和非线性控制； 孙秀霞(1962-)，女，山东潍坊人，教授，博士生导师，主要研究方向为无人机控制、导航理论与应用。

V249.1

A

1002-0853(2015)06-0527-05