改进Apriori算法在高校学生信息系统中的应用研究

胡淑新，李长云，吴岳忠

（湖南工业大学 计算机与通信学院，湖南 株洲 412007）

随着近年来大数据的兴起，一个热点问题便是数据挖掘，数据挖掘其实是一种决策支持过程，在高度自动化的分析大量数据后，可以做出归纳性的推理，继而从中挖掘出潜在的模式，之后可以给予决策者有效判断的依据。其中，作为非常重要的研究方法之一，关联规则主要反映的是事物之间的依存和关联问题，如果几个事物之间存在一定的关联性，那么，可以通过其他事物预测到之中的某个事物[1]。找出关联规则的关键步骤：1)找出所有频繁项集。2)分析频繁项集从而得出满足最小信任度阈值的规则。1993年由Agrawal等人提出了挖掘算法，之后又进一步提出了Apriori算法，该算法是一种挖掘关联规则的频繁项集算法，其思想是通过候选集生成和情结的向下封闭检测两个阶段来挖掘频繁项集[2]。

1 Apriori算法概述

Apriori算法是一种最有影响的挖掘布尔关联规则频繁项集的算法。该算法的核心是基于两阶段频集思想的递推算法，使用一种逐层迭代的方法通过低维频繁项集得到高维频繁项集，因而在使用中会有很多的不足之处[3]。

Apriori算法的计算复杂度4个因素的限制：1）最小支持度阈值和最小置信度阈值；2）项数（维度）；3）事务数；4）事务的平均宽度[4]。该算法存在一些缺陷：1）候选项集的逐层产生需要频繁扫描整个数据库，直到无法再产生候选集为止。2）可能产生大量候选集。Apriori算法应用十分广泛，图书馆系统，高校管理系统等，并且在近年来像移动通信领域的应用也呈现出强劲的发展势头，将该算法应用与各种数据的相关挖掘处理从而得到用户的行为特征和一些动态的信息作为决策参考[5]。

由于Apriori算法的一些明显缺陷，研究者们不断地提出各种改进方案，常见的有3种优化方法：1）基于矩阵的优化方法，在算法中运用矩阵的思想，将事务数据用矩阵的形式来表示。2）基于划分的优化方法，在算法中运用分块的思想，将数据库逻辑上分成几个相对独立的块单独考虑，最后合并频集。3）基于采样的优化方法，在前一遍扫描的基础上来组合分析[6]。

2 以数组向量为存储结构改进Apriori算法

2.1 基于数组向量的算法改进

对传统的Apriori算法进行改进，借鉴文献[7]的思想，在此基础上，更改数组向量的数据结构，每个数组向量多设定一列来记录事务数组的数目，将事务数据库的每个事务数据映射到事务数组向量中，根据长度的不同存入不同列大小的二维数组中，行代表事务，列代表项，这样就可以将数据库的信息投影到内存中，降低了访问时间。相同的事务项只在数组中存储一次，压缩了相同事务在内存中的数目，每一行的最后一列记录该行事务数组数目，这样对数据库扫描一次以后就在内存中建立了一个投影的数组向量，之后的扫描都只需扫描改数组向量即可，降低了扫描次数和I/O负载。约定各事务项目、频繁项集以及候选项集中的各项都是按照其代表的项目的字典次序排列。

改进的Apriori算法在高校学生信息管理系统中应用的算法框架如下：

输入：事务数据库D，最小支持度supmin;输出：数据库中的频繁项集L。

二维数组Ai(i=2,3…,n+1); //将事务根据长度不同放入不同列大小的数组中

步骤 1：1)L1=find_frequent_1_itemset(D); //扫描事务数据库D，将每个事务数据库按照长度不同存储在数组向量A中，数组A的最后一列记录对应的该行事务的数目，再根据最小支持度supmin找到频繁1项集L1。

步骤2 2)for(k=2;Lk-1≠0.;k++)

3){Ck=apriori_gen(Lk-1,supmin); //根据频繁（k-1）项集Lk-1生成候选K项集Ck。

4) {for(i=k+1;i＜n+1;i++) //扫描数组向量 A，n为A包含数组向量的个数。

5)for(j=0;j+1＜ni;j++) //扫描每个事务除事务数组向量的最后一列记录的数目以外

6){CAi[j]=subset(Ck,Ai[j]);

7)foreach c∈CAi[j]

8)c.count+=Ai[j+1]}} //读 取 Ai[j]事 务 的数目记录到Ai[j+1]中

9)Lk={c∈Ck∣c.count≥supmin};}

10)return L=UkLk;

apriori_gen(Lk-1,supmin)函数主要完成两个目标：

1)连接操作

根据频繁（k-1）项集Lk-1生成候选k项集Ck。

Apriori算法性质：对于k项集Mk，频繁k项集包含的频繁k-1项集出现的次数应该大于等于k。根据该性质频繁（k-1）项集与自身连接生成候选k项集之前，需要先计算出频繁项集Lk-1(j)的所有项目的频度，如果Lk-1(j）的频度＜k-1,记录下来，然后在频繁项集Lk-1中删除掉包含刚才记录的频繁项目集中任一元素的项目集。就可以得到一个更小的频繁(k-1)项集的集合，在对该集合中的频繁项集自身连接之前先对它进行判断，如果它的数目小于等于1时，得出结论候选K项集Ck为空。否则，根据有序的频繁项集的项，包含于该集合中的任意两项不同的频繁(k-1)项集X与Y连接进行比较，如果不能连接，即两项之后的所有频繁(k-1)项集都不能满足连接条件，所以不用再判断X与Y以后的所有频繁(k-1)项集，该操作减少了连接中比较的次数，缩短了时间。

2)修剪操作

修剪的功能与Apriori算法相同，根据Apriori算法的性质：对于k项频繁项集Lk，如果事务的长度小于k时，计算候选k项集Ck的频度时，改事务项不必再扫描。最终可以得到候选K项集Ck。

2.2 改进Apriori算法在高校学生信息系统中的应用

1)使用计算机专业12级部分本科生的部分成绩作为原始数据库事务集进行举例说明

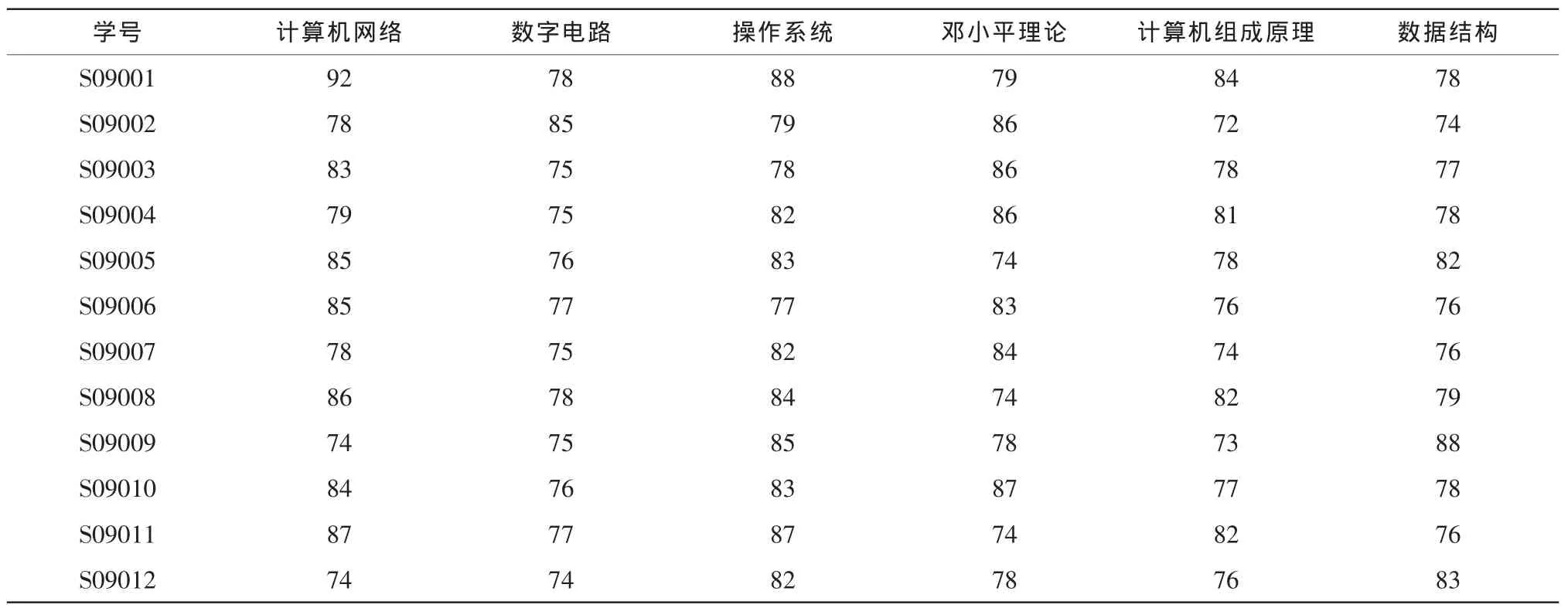
表1 原始数据库Tab.1 Original database

2)对原数据进行预处理得到事务集D

对数据进行格式转换，采用逻辑型数据，将成绩数据用布尔型数据表来表示，80分以上的用 “1”来表示，80分以下的用“0”来表示，将学号用 S1…S12 来表示，课程用 B、C、D、E、F、G分别表示计算机网络、数字电路、操作系统、邓小平理论、计算机组成原理、数据结构，这样存储可以大大节省存储空间。

3)采用改进后的Apriori算法对事务集D进行扫描后得到数组向量A（表2所示）以及候选1项集C1、支持度supmin和频繁1项集L1（表3所示）。数组A的最后一列用来记录各事务的数目。设定最小支持度为2/12。

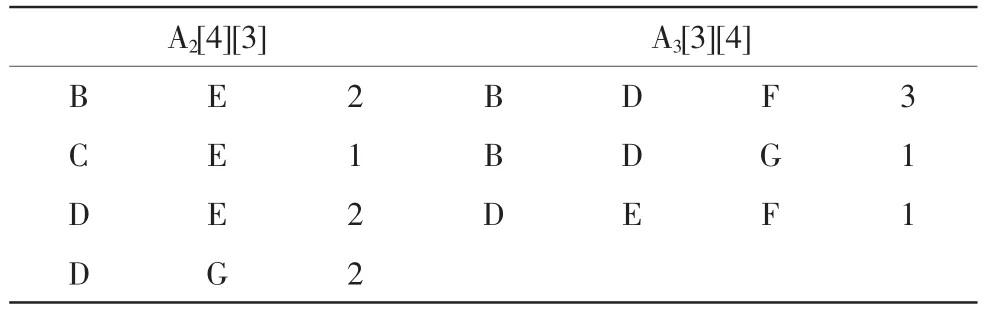
表2 数组ATab.2 Array A

表3 候选1项集以及频繁1项集Tab.3 Candidate item sets and Frequent item sets

4)通过频繁1项集得到候选2项集C2以及频繁2项集L2在计算支持度的时候，对于有相同事务的项集只需要扫描一次，通过找到对应的A2[0][2]=2,A2[2][2]=2,A2[3][2]=2,A3[0][3]=3存储的计数，最后得到频繁2项集。

5)根据频繁2项集可以求得候选3项集,首先分析频繁2项集中 B的频度为3，D的频度为 4，E的频度为2，F的频度为2，G的频度为1，因为G的频度＜2=3-1，所以根据前边所诉Apriori算法的性质，删掉频繁2项集中包含G的频繁项目，从而得到删减后的频繁过度2项集，然后与自身相连接，根据前边所讲解的连接判断得到候选3项集C3={{B，D，E}，{B，D，F}}。

6)重复以上第5步的方法，得到频繁3项集L3={{B，D，F}}。连接获得候选4项集，但由于频度均小于3，所以候选4项集为空，所以算法结束。

7)由最长的频繁集L3产生的关联规则及由次长的频繁集L2产生的关联规则如表4所示。

根据已经设定的最小支持度为2/3，置信度为1，可以得到筛选后的较强的关联规则。

选出规则{{G}}==＞{{D}}[support=3/12，confidence=1]分析

可知数据结构为“优”操作系统为“优”的置信度为1。分析关联规则，从来理论上来讲，部分规则是有实用价值的，最后的规则仍需根据现实意义进行删减。G表示的是数据结构成绩，D表示的是操作系统成绩，那么它的意义就是当数据结构的成绩处于优秀，相应的操作系统的成绩也应该处于优秀水平，现实中，数据结构作为操作系统的一门必修先行课程，说明数据结构确实是学习操作系统的一门必要的先修课程。不可否认，Apriori算法给出了很多现实中我们认为是无用关联的信息，一方面是由误差引起的，当然也与数据集的大小有关，这是以后算法改进时需要考虑的问题。

表 4频繁3项集关联规则及频繁2项集关联规则Tab.4 Association ru les in frequent item sets of size 3 and Association rules in frequent item sets of size 2

3 可信度算法性能分析及实验

找数据的时间效率提高，只需访问数组中记录该事务数目的项，时间复杂度为O（1）。原Apriori算法的扫描数据库的次数为为候选K项集的大小）。改进算法相比原算法在一定程度上减少了运算量。

2)空间复杂度方面，原算法会产生大量的候选项占用内存，并且会频繁的进行I/O访问，改进的Apriori算法相同的事务项在数组中只存储一次，占用了很少的内存空间，也减少了进行I/O访问的次数。采用改进后的算法进行数据挖掘将

改进后的基于数组的Apriori算法[8]与经典的Apriori算法相比，优点如下：

1)算法对数据库的扫描次数减少，只需扫描一次，减少了访问事务的次数，并且采用了合理的结构来表示事务项，寻可以大大减少内存占用率。

3)改进的Apriori算法的数据结构相比原算法大大简化，使用简单的数组来访问以及存储可以节省时间，并且扫描一次数组的效率远高于原算法的扫描一次事务数据库的效率。

实验结果及分析：

为了验证改进算法的效率，对原Apriori算法和改进算法进行对比试验，数据集为计算机专业12级部分本科生成绩，数据集包含了300名学生的21门课程，共6 300条记录，对预处理后的数据集进行测试。试验环境为：Inter(R)2.40GHz CPU，1G内存，操作系统为Windows7，算法在matlab 2010b下实现。多次测试，取其稳定后的试验结果。两种算法的性能比较如图1所示。

图1 图1同一最小支持度下的时间性能比较Fig.1 Time performance comparison on sameminimum support

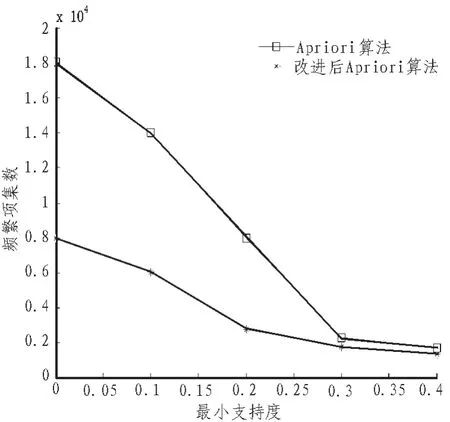
图2 不同支持度下产生的频繁项集个数Fig.2 Frequent itemsets in different support

由图1可以看出原Apriori算法与基于数组向量改进后的算法在同一最小支持下的时间性能。从仿真的试验结果中可以看出，当最小支持度的值增大的时候，传统的Apriori算法与改进后的算法相比，时间开销相差不是很大，主要是因为较高的支持度会使得候选项集大大减少，所以减少了算法扫描数据库时的时间开销。由图2可以看出在不同支持度下的原Apriori算法与改进后的算法产生的频繁项集的个数不同，随着支持度的增大，产生的频繁项集的个数相差减小，当支持度较小时，可以很明显的看出改进后的算法产生的频繁项集的个数远远少于原算法产生的个数。

4 结束语

文中对于Apriori算法进行了分析，对于其复杂性以及缺陷提出了一种改进方案，主要是从减少扫描事务数据库的频度、提高算法对于内存的利用率方面改进，通过实验分析验证了改进算法的有效性。将改进后的Apriori算法应用于高校学生信息系统中，将对课程建设的合理性和教学水平的提高有很大的实用价值，对于课程开设的顺序以及要开设哪些课程如果还是像以往一样单凭经验去决定，无法科学准确的给予学生开设最需要的课程，通过挖掘学科之间的关联规则，可以客观的去了解它们的关系，有助于今后的课程安排，关联规则挖掘在高校中的应用将会越来越多。

[1]Han J,Pei J,Yin Y.Mining frequent patternswithout candidate generation[C]//Acm Sigmod Record,2000,29(2):1-12.

[2]林郎碟,王灿辉.Apriori算法在图书推荐服务中的应用与研究[J].计算机技术与发展,2011(5):22-24，28.

[3]Agrawal R,Imieliński T,Swami A.Mining association rules between sets of items in large databases[C]//ACM SIGMOD Record.ACM,1993,22(2):207-216.

[4]Toivonen H.Sampling large databases forassociation rules[C]//VLDB,1996(96):134-145.

[5]何月顺.关联规则挖掘技术的研究及应用[D].南京：南京航空航天大学,2010.

[6]陈伟.Apriori算法的优化方法[J].计算机技术与发展,2009(6):80-83.

[7]林佳雄,黄战.基于数组向量的Apriori算法改进[J].计算机应用与软件,2011(5):268-271.

[8]刘宗成，张忠林，田苗凤.基于关联规则的网络行为分析[J].电子科技,2015(9):16-18.