基于PCA的口语课堂教学质量评价模型研究

胡 帅，顾 艳，曲巍巍

（渤海大学大学外语教研部 辽宁 锦州 121013）

高校教学质量评价是一个多维、非线性分类问题[1]，一般来讲，如果教学质量的评价指标越多，越能够较为全面地反映教师的教学质量，但在实际评价过程中，评价指标过多必然导致数据过于庞大，且数据的采集和统计过程过于繁琐，这无疑会增加数据处理的复杂性，主成分分析(Principal Component Analysis，PCA)是一种基于变量协方差矩阵来实现数据降维的处理方法，可以有效降低原始数据中多余信息干扰，提取原始数据的核心指标信息[2-3]。文中将PCA方法应用于高校课堂教学质量的评价中，基于MATLAB R2013a平台，编程对原有的复杂评价指标体系进行简化，建立了教学质量评价模型，并对某省属本科院校的8位外语教师的课堂教学质量进行评价实验，验证所建模型的实用性。

1 PCA算法基本原理

PCA算法的实质是找出各复杂因子的主成分,实现指标的简化，即数据降维[4]。PCA具体算法如下[5-6]：

1)将原始数据标准化。假设有n个样本，每个样本有p个指标 X1，X2，X3，…，Xp，由于指标量纲不同，数量级相差较大，所以在进行主成分析之前，需对原始数据作标准化处理。标准化的目的是使平均值为0，标准差为1。

2)计算相关系数矩阵 R。 式(1)中 rij(i，j=1,2，…，p)代表 Xi和Xj之间的相关系数。

3)计算R的特征值与特征值的贡献率和累计贡献率。按照式(2)计算R的特征值，第k个主成分的贡献率如式(3)所示，前k个主成分的贡献率如式(4)所示。一般情况下，当累计贡献率达到85%以上时，即可用这k个主成分代替原来的p个指标，且此时保留了损失原始数据的绝大部分信息。

4)计算R的特征向量如式(5)所示。

5)计算主成分系数矩阵。由式(5)进一步写出主成分系数矩阵如式(6)所示，式(6)中(k=1,2,…,p)为经过标准化处理后的第k个指标。

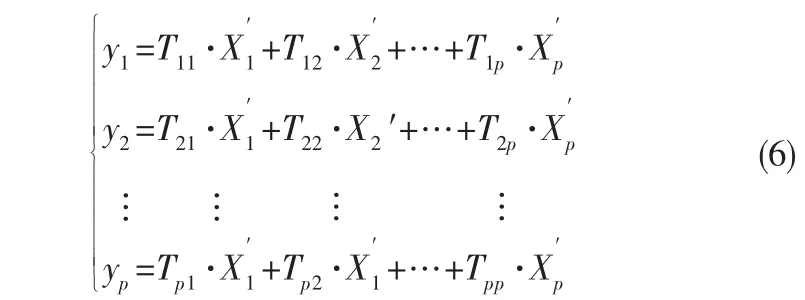
6)构建综合评价函数。将式(3)代入式(7)可得第n个样本的综合评价函数。

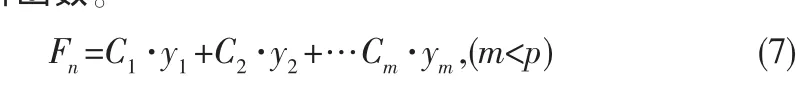
2 基于PCA的教学质量评价模型建立

文中以某高校8位英语教师的口语课堂的教学质量为研究对象，建立基于PCA的口语课堂教学质量评价模型。

2.1 模型的评价指标体系

本文依据普通高等学校教学工作水平评估指标体系，结合师生调查问卷，同时咨询该领域专家，最终建立了包括教务部门、学生、同行3部分的评价指标体系。

其中教务部门评价的一级指标是师德，具体包括遵守规章制度（X1）；无无故缺勤，迟到或早退（X2）。学生评价一级指标是教学内容，包括重点、难点处理得当（X3），理论联系实际（X4）；教学方法，包括教学方法适宜，因材施教（X5）；教学态度，包括授课有热情、情绪饱满（X6）；尊重、爱护学生（X7）；教学效果，包括学生学习积极性高（X8），内容为大多数学生掌握（X9）。 同行评价包括教研活动（X10），科研能力（X11）和爱岗敬业（X12）。

2.2 模型的原始数据采集

为了提高模型分析的准确性和评价信度，保证数据的科学性，本文将采集到的最初数据中的倾向性数据（即评分全部为满分或全部为零分的数据）剔除，保留有效数据后，计算每位教师的各指标的平均得分，进而获得用于教学质量评价的原始数据表如表1所示。

2.3 模型的主成分选取

从表2可见，前4个主成分特征值大于1，方差累计贡献率为89.34%，按主成分选取原则，只要选用的主成分能够保留原始信息量的85%以上即可[7]，故文中选取前4个主成分，信息的损失率为10.66%，表明前4个主成分具有显著代表性，能起到压缩数据量的作用。

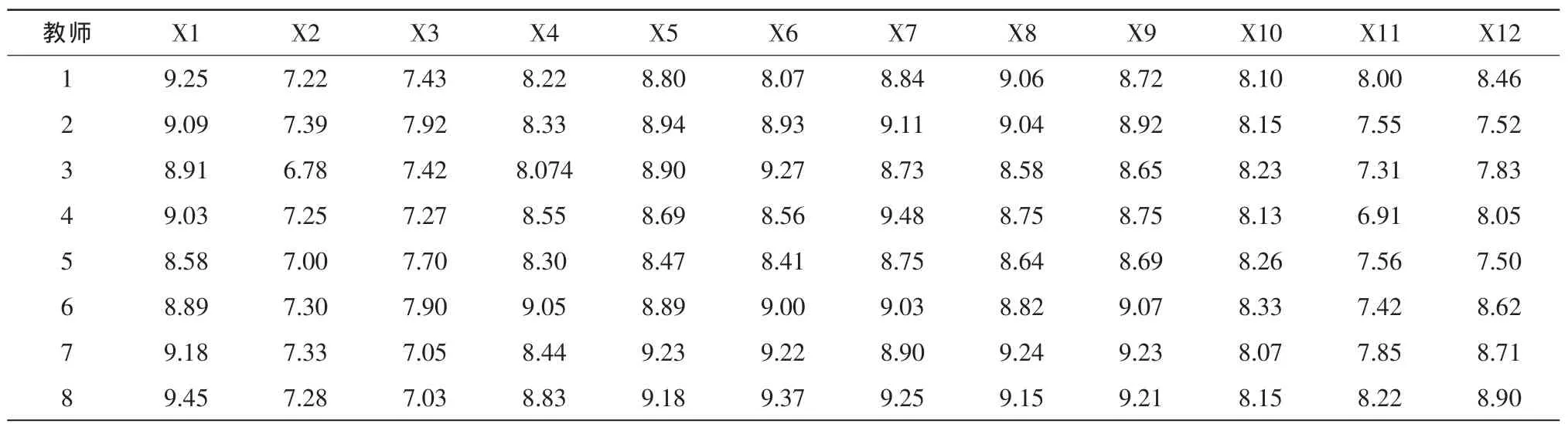
表1 教学质量评价原始数据表Tab.1 Original data table of teaching quality assessment

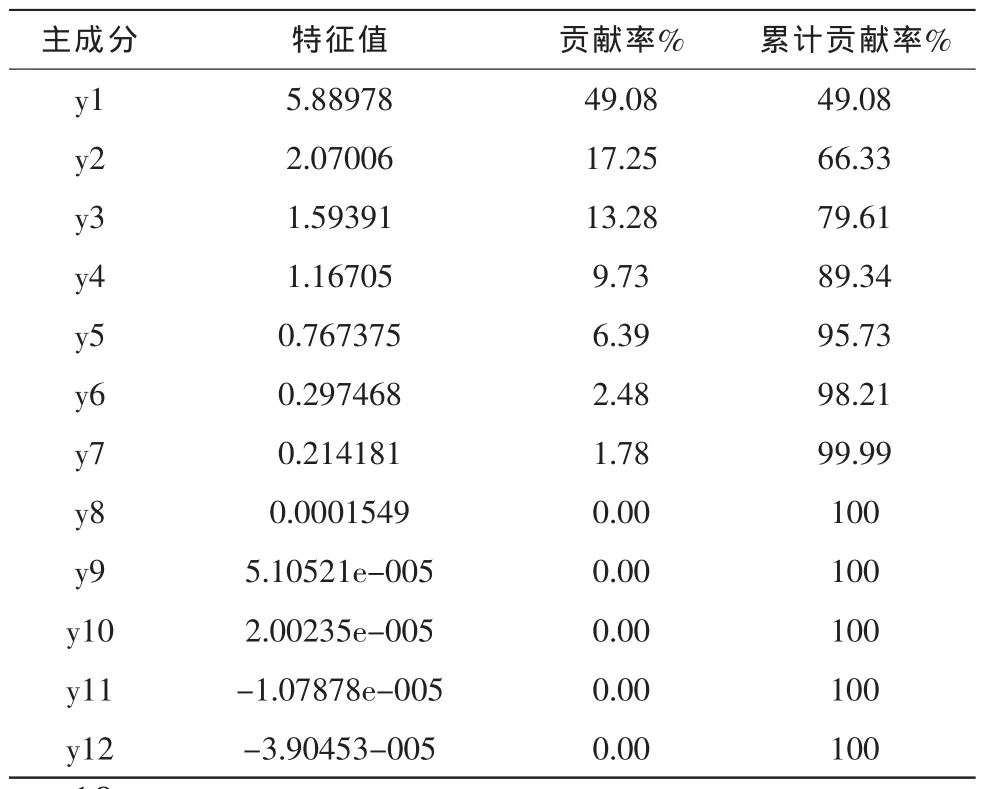
表2 主成分特征值、贡献率与累计贡献率Tab.2 Eigenvalues,contribution rates and accumulative contribution rates of principal components

2.4 模型的主成分得分

将表3中的数据代入式(6)可以写出4个主成分的得分系数表达式，如式(8)～式(11)所示，式(8)～式(11)中表示表1中的原始数据经过标准化处理后的结果。

由式(8)可以知道，对主成分y1影响较大的权重系数为0.3713，0.3614，0.3606，0.3597，0.3371,它们分别对应因子、反映了这五个变量与教学质量密切相关；由

利用计算得到的主成分载荷矩阵除以每个主成分特征根的均方根可以得到12个主成分的特征向量，由上一节可知，本文最终选取前4个主成分，所以可以得到前4个主成分特征向量如表3所示。式 (9)可知，对主成分y2影响较大的权重系数为0.5747，0.4710，0.3100，它们分别对应因子、、，反映了教师课堂教学内容及方法；由式(10)可知，对主成分y3影响较大的权重系数为0.5124，-0.4970，-0.4371，它们分别对应因子反映了教师对学生及其教学工作的态度；由式(11)可知，对主成分y4影响较大的权重系数为-0.4852,对应因子X11′，反映了教师的科研能力。综上所述，前4个主成分可以完全代表原始12个指标所反应的信息。

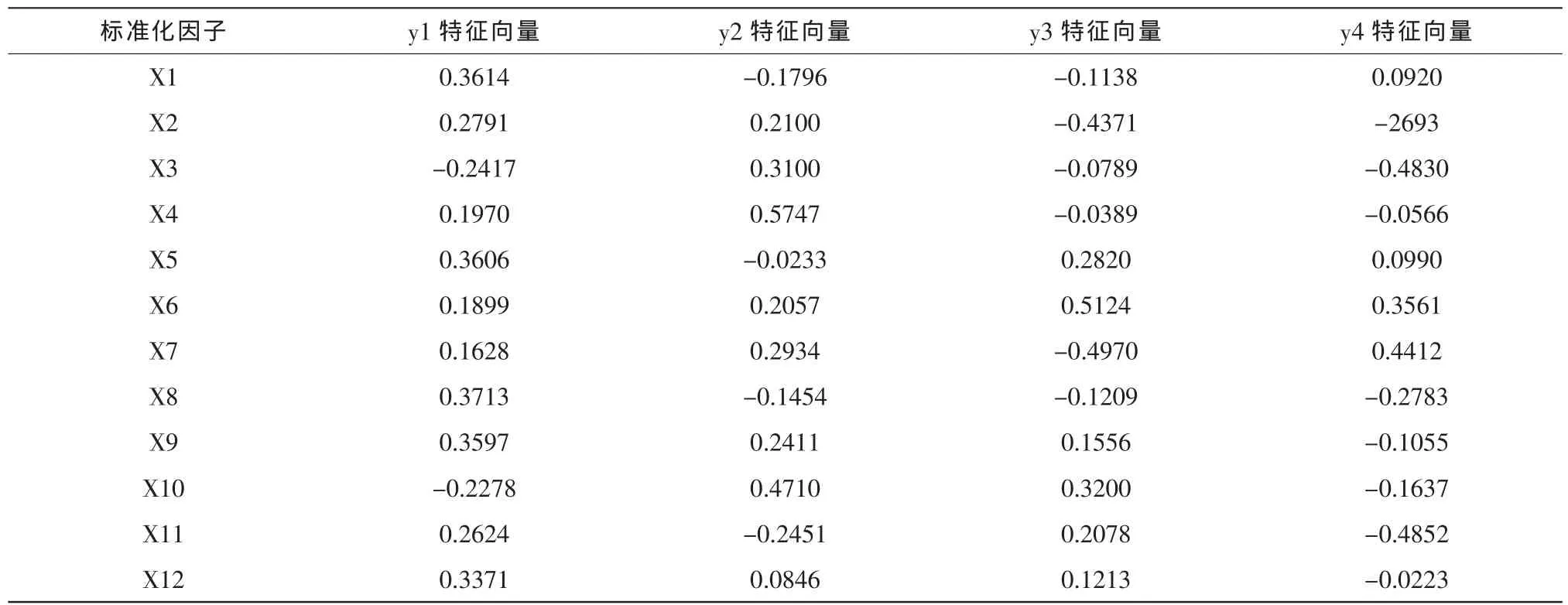
表3 前4个主成分特征向量Tab.3 Eigenvectors of the first four principal components

将前4个主成分的贡献率和式(8)～式(11)的结果代入式(7)可以构造主成分得分综合评价函数如式(12)所示。根据式(12)，可计算得到8位教师的教学质量评价得分与排名如表4所示。由表4可以看出，主成分综合排名与传统总成绩排名基本一致，只有教师1和教师4的排名略有不同，这主要是因为根据大数定理，样本数越大，样本标准化结果越稳定，模型评价准确率越高，所以，可以通过增加样本数量进一步提高模型评价准确率。

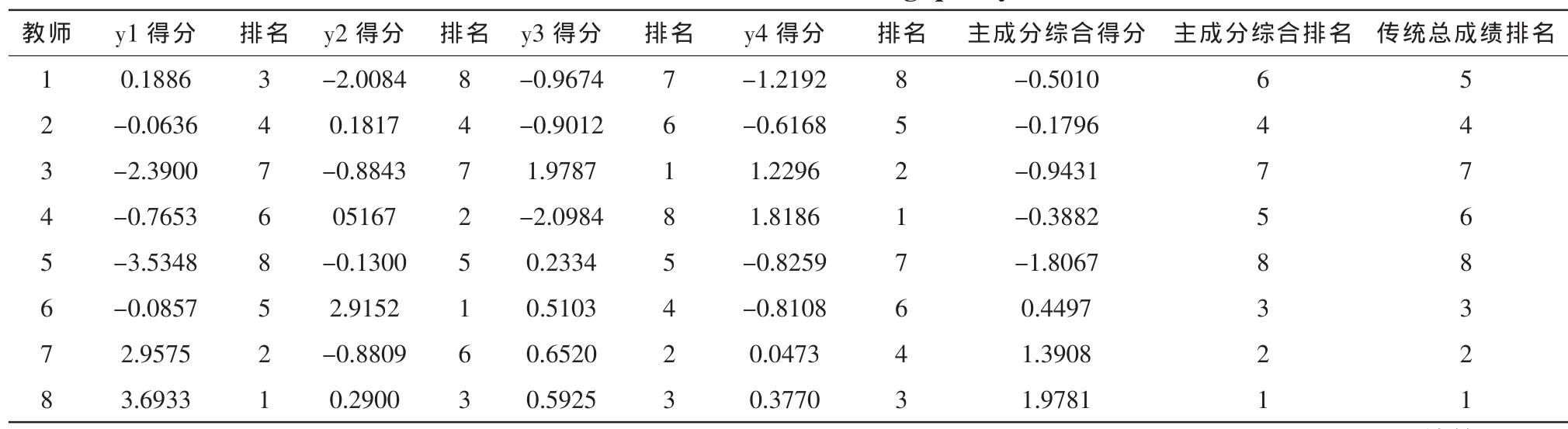
表4 教学质量评价得分与排名Tab.4 Scores and ranks of teaching quality assessment

3 结论

文中通过主成分分析法对复杂的教学质量评价指标进行筛选，将最初的12项教学质量评价指标体系简化为4项，消除了原有指标间的信息重叠，以主成分贡献率作为综合评价函数的权重系数，消除了主观因素对评价的影响成分，最终构建了1个综合评价函数对教师教学质量进行定量评价，简化了评价过程，提高了评价指标质量，验证了所建评价模型的有效性。

[1]喻朝阳AHP-PCA-SVM的高等数学教学质量评价[J].科技通报,2013,29(10):229-231.

[2]冷泳林,王悦.主成分分析法在学生评教中的应用研究[J].信息技术,2012,(12):11-14.

[3]姜波.多元统计分析方法在实际问题中的应用[J].沈阳师范大学学报(自然科学版),2012,30(4):465-468.

[4]孙健,王成华,洪峰,等.基于PCA-LVQ的模拟电路故障诊断[J].电路与系统学报,2013,18(2):310-313.

[5]钱玉良,张浩,彭道刚,等.PCA和GA-PSO-RBF集成的发电机组远程故障诊断[J].电子测量与仪器学报,2012,26(7):597-604.

[6]付忠广,王丽平,戈志华,等.采用主成分分析法综合评价电站机组的运行状态[J].动力工程,2008,28(4):548-551.

[7]仝美红,段富.基于主成分分析和熵值法的高校教师绩效评价[J].计算机应用与软件,2014,31(1):62-64,169.