纤维体积分数对三维编织复合材料T型梁模态性能的影响

王 欢，李嘉禄，樊 威

(天津工业大学 复合材料研究所 天津市和教育部共建先进纺织复合材料重点实验室，天津 300387)



纤维体积分数对三维编织复合材料T型梁模态性能的影响

王 欢，李嘉禄，樊 威

(天津工业大学 复合材料研究所 天津市和教育部共建先进纺织复合材料重点实验室，天津 300387)

采用悬臂梁自由衰减振动的实验方法研究了碳纤维三维四向编织复合材料T型梁的模态性能，分析了纤维体积分数对其固有频率和阻尼的影响。将实验得到的固有频率结果与有限元得到的固有频率结果作了对比。结果表明：三维四向编织复合材料T型梁的模态性能与激振点位置无关。且其固有频率随纤维体积分数的增大而提高，阻尼性能随纤维体积分数的增大而降低。通过阵型可以准确判断T型梁固有频率的阶数。实验结果与计算结果相一致。

三维四向编织；复合材料T型梁；模态分析

三维编织复合材料是由具有多轴纤维取向的高度整体化的连续纤维集合体增强的复合材料，由于增强体的整体性，显著提高了复合材料整体的刚度和强度, 并且使复合材料具有减振性好、抗疲劳性佳、材料性能可设计等特点。因此可以在许多部件上替代金属材料以满足航空航天领域减重和承载性能的要求，也为其应用于主承力结构件提供了深远而广阔的应用前景[1,2]。随着它在航空、航天等领域的广泛应用，研究三维编织复合材料的模态性能，提高其在振动和噪声环境下的可靠性，从而避免在使用中因共振造成不必要的损失是十分必要的。

目前，关于这类材料的模态性能已有科研人员进行研究。蔡敢为等[3]研究了三维编织纤维增强复合材料连杆机构的模态阻尼，导出了此类复合材料的细观结构参数、组分材料性能参数、纤维体积比等与机构的固有频率、振型和模态阻尼等参数之间的关系。李典森等[4]对不同编织角、不同体积分数的三维四向和五向玻璃纤维编织复合材料进行了振动阻尼实验，分析了编织角、纤维体积分数和编织结构对三维编织复合材料阻尼特性的影响。孙雨果等[5]在建立有限元模型基础上，对三维碳/环氧编织复合材料等网格承力筒结构的静力学性能和模态进行了分析,得到了该结构的固有频率和模态振型。裴晓园等[6,7]研究了编织角及纤维体积分数对碳纤维三维四向编织复合材料的模态性能影响，实验表明，随纤维体积分数的增大，碳纤维三维四向编织复合材料的固有频率增大，阻尼性能下降。Gao等[8]采用实验方法研究了编织角对三维五向编织复合材料模态性能的影响。Ooijevaar等[9]将振动实验与模态应变能损伤算法相结合，对铺层T型梁的损伤位置做出了准确的定位。研究得出：弯曲模态固有频率可表明分层的存在，部分阵型可表明分层的存在及其位置。Herman等[10]利用振动模态分析方法检测了T型加筋板的损伤。Lee等[11]基于经典的层合理论研究了工字形截面复合材料薄壁梁的振动。Thinh等[12]用实验方法和有限元方法研究了带有不同形状加强筋的玻璃纤维增强聚酯基复合材料的自由振动。Alnefaie[13]利用三维有限元模型计算了分层纤维增强复合材料板的固有频率和模态位移。本工作对三维编织复合材料T型梁制件的模态性能进行了研究。采用单输入/单输出和单输入/多输出的频域模态参数识别方法，对三维四向碳纤维编织复合材料T型梁的模态性能进行了研究，确定了纤维体积分数对复合材料T型梁模态参数( 阻尼比、固有频率)的影响，并将实验获得的固有频率结果和有限元计算结果作了对比。

1 实验描述

1.1 测试试件

三维四向编织复合材料T型梁试件采用四步法编织工艺，再经RTM工艺复合固化制得。编织纱为 T700-12K 碳纤维，密度1.76g/cm3，线密度0.8g/m，基体材料为TDE-86 型环氧树脂。图1为试件的实物图，实验中T型梁试件的长度为280mm，其中实验的有效尺寸为255mm。试件的详细尺寸如图2所示，其具体参数见表1。

图1 三维四向编织复合材料T型梁试件实物图Fig.1 The picture of specimen of three-dimension and four-direction braided composites T-beam

图2 T型梁试件的尺寸Fig.2 The size of T-beam specimen

NumberofsampleSurfacebraidingangle/(°)Volumefractionoffiber/%QuantityV129383V229513V329613

1.2 测试方法

本实验采用一端固支悬臂梁的自由振动衰减法测量T型梁模态性能，振动模式为y向弯曲振动，实验环境温度为室温。实验装置示意图如图3所示。用力锤在激振点沿y方向激振，力锤上的力传感器感受的力信号经电荷放大器放大后输入到数据采集仪的1 号通道，同时加速度传感器测量的加速度响应信号经电荷放大器放大后输入到数据采集仪的 2 号通道，再由Vib′SYS模态分析软件进行分析计算，得到频率响应函数。本次实验还选取了不同的激振点进行测试，A点(图2)和B点为所选取的不同的激振点，其中A点位于远离腹板一侧的肋板平面上，B点位于腹板外侧沿Z轴的中心线上，且它们都距T型梁的顶端245mm，如图3所示。在实验中分别采用单点激励单点响应和单点激励多点响应的方法。

2 实验结果与讨论

以B点为激振点，分别对不同纤维体积分数的三维四向编织碳纤维/环氧树脂复合材料T型梁进行悬臂梁振动实验模态分析(每一种纤维体积分数，有3个试件进行实验)，获得了各个模态参数的平均值( 阻尼比、固有频率)，见表 2。

图3 模态实验测试装置图Fig.3 The device for modal experimental measurement

NumberofsampleNaturalfrequency/HzDampingratio/%FirstorderSecondorderFirstorderSecondorderV1213．871408．281．300．80V2261．281616．061．100．53V3290．151773．000．970．37

2.1 不同激振点的测试

图4 T型梁在A，B点激励后频率响应函数图的对比Fig.4 The comparison of frequency responses of T-beam excited at points A and B

本实验选择A，B两个不同的激振点对三维四向编织复合材料T型梁的模态性能进行测试。图4是分别对纤维体积分数为61%的T型梁的A，B两点进行激振，得到的频率响应函数图，这两条曲线的吻合性较好。获得的峰值中最大的相对标准偏差为0.12%。由于所有的相对标准偏差都不超过1%，所以实验中得到的固有频率值具有很好的重复性，这也与Ooijevaar等[9]得到的结果相一致。因此在之后的实验中就选取B点为激振点。

2.2 纤维体积分数对三维四向编织复合材料T型梁固有频率的影响

图5是相同表面编织角、不同纤维体积分数的三维四向编织复合材料T型梁试件的前两阶固有频率的对比，可以看出前两阶固有频率都随着纤维体积分数的增加而增大。根据梁的振动理论，悬臂梁的一阶振动频率服从以下关系[14]：

(1)

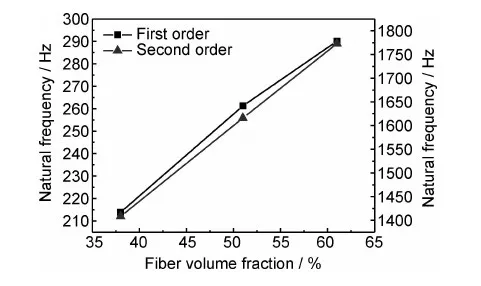
图5 不同纤维体积分数T型梁固有频率的对比Fig.5 The comparison of natural frequencies of T-beam with different fiber volume fractions

式中:k1为对应一阶频率的系数(取1.875)；l为梁的长度， mm；E为梁的弹性模量，GPa；h为平行于梁振动方向的高度，mm；ρ为梁的质量密度，g/mm3。由公式(1)可见，当梁的外部尺寸相同时，梁的一阶振动固有频率正比于梁的比模量的平方根。由于三维四向编织复合材料T型梁的纤维刚度远远大于基体的刚度，所以纤维体积分数的增大就意味着整体刚度的增大，即梁的弹性模量增大。因此三维四向编织复合材料T型梁的固有频率随纤维体积分数的增大而升高，故实验结果是合理的。

图6是不同纤维体积分数的三维四向编织复合材料T型梁在激振力作用下的传递函数幅值图。可以看出随纤维体积分数的增大，各阶峰值所对应的固有频率增大。固有频率是由系统本身的质量、形状和刚度所决定[4]，相同尺寸的碳纤维三维四向编织复合材料T型梁，其材料的弹性模量越大，则刚度越高，因此梁的固有频率也越大。固有频率越高表明其在脉冲载荷作用下的抵抗变形能力越大，即其抗弯刚度大。碳纤维三维四向编织复合材料T型梁的固有频率越高，在实际使用中就越不容易达到其共振频率，即避免发生共振的可能性越大。所以为提高三维四向编织复合材料T型梁的固有频率，在实际应用中应适当地增加其纤维体积分数。

图6 不同纤维体积分数T型梁频率响应函数图Fig.6 The frequency response plot of T-beam with different fiber volume fractions

2.3 纤维体积分数对三维四向编织复合材料T型梁阻尼比的影响

阻尼通常是指材料内部在经受振动变形过程中，将机械振动能转变为热能耗散掉的能力。它是试件的固有特性，在振动过程中耗散能量，对降低共振区峰值十分重要[15]，可以避免结构因振动应力达到极限而造成的破坏。阻尼性能越好，将振动能转化成为热能耗散掉的能力越强，这是阻尼减振性能的本质所在。因此，三维四向编织复合材料T型梁的结构设计中同样要考虑阻尼因素。复合材料制件的刚度由纤维增强体确保，在保证复合材料制件刚度的同时，也需要适当增大其阻尼性能，以获得良好的减振效果。

阻尼比可以通过半功率带宽的方法计算得到，如图7[16]所示，同时根据以下公式可以得到其阻尼比：

(2)

式中：ωn是由极值点对应的固有频率；Δω是ω2与ω1两个点的差值。故结合公式(2)可以从图6中看出试件的固有频率越小，对应的峰值越低、越宽，所得的阻尼比越大；试件的固有频率越大，对应的共振峰值越高、越尖锐，所得的阻尼比越小。

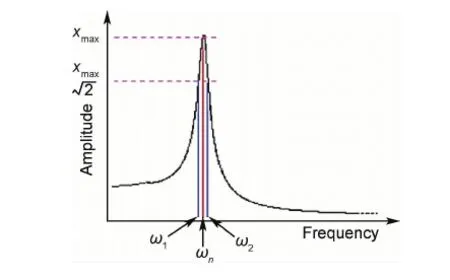
图7 根据半功率带宽的方法定义ω1，ω2与ωn[15]Fig.7 Definitions of ω1，ω2 and ωn according to the half-band width method[15]

图8 不同纤维体积分数T型梁阻尼比的对比Fig.8 The comparison of damping ratios of T-beam with different fiber volume fractions

图8是相同表面编织角、不同纤维体积分数的三维四向编织复合材料T型梁试件的前两阶阻尼比的对比，可以看出前两阶阻尼比都随着纤维体积分数的增加而降低。这是由于基体良好的黏弹性质，使得树脂基体具有较高的振动衰减损耗因子，它在复合材料中起到很好的阻尼作用。所以纤维体积分数越低，制件的黏弹性效应也越明显。反之随着纤维体积分数的增加，即基体含量的减少，使得基体对复合材料制件的衰减损失因子贡献减小。因此，纤维体积分数低的试件的振动衰减性能比纤维体积分数高的试件优异，即前者的阻尼比要比后者的大。这也说明了在相同的共振情况下，纤维体积分数低的T型梁比纤维体积分数高的T型梁回到平衡位置的时间要短。从图8中还可以看出相同纤维体积分数的第二阶阻尼比都比其第一阶阻尼比低，这可能是由于梁在二阶振动时，接近梁的中心存在很大的振动幅值[13]。

2.4 三维四向编织复合材料T型梁的阵型

振型是结构所固有的属性，它不取决于作用在结构上的力或者载荷。如果结构的材料属性(质量、刚度、阻尼)或者边界条件发生变化，阵型就会改变。阵型是指在共振时一个点相对于另一个点的运动情况，它是独一无二的。对应于频率而言，一个固有频率对应于一个振型。按照频率从低到高排列为一阶振型，二阶振型等。实际结构的振动形态并不是一个规则的形状，而是各阶振型相叠加的结果，然而在共振频率或者共振频率附近的振动形态是以一个单一的阵型为主。在实际应用中，可以用阵型来判定损伤的位置。本实验采用单点激励多点响应的方法研究三维四向编织复合材料T型梁的阵型，激振点有1个(B点)，响应点有5个，它们将T型梁的有效长度沿着z轴的方向平均分成5份，如图9所示。图10(a)，(b)分别是纤维体积分数为61%的T型梁的一、二阶弯曲阵型图。通过测量三维四向编织复合材料T型梁的阵型，可以看出它的振动形态，也可以更加准确地断定其固有频率的阶数。

图9 T型梁上的激振点和5个测量点Fig.9 Excitation point and 5 measurement points at T-beam

图10 实验测量的弯曲阵型 (a)一阶弯曲阵型；(b)二阶弯曲阵型Fig.10 Experimental measured bending mode shape (a)first bending mode shape;(b)second bending mode shape

3 有限元计算与模拟

本工作运用ANSYS软件建立了T型梁的实体有限元模型，计算与模拟了T型梁的固有频率和阵型。按照复合材料的理论，三维四向编织复合材料是横观各向同性的，所以在模拟中选取的材料属性为orthotropic。采用六面体划分网格，共划分了52480个单元，129283个节点。对T型梁的端部固定约束，然后计算。计算中采用的弹性性能数据来自于李典森等[17]的有限元计算，三维四向编织复合材料的弹性性能见表3。T型梁的前两阶弯曲阵型位移云图如图11所示，计算的频率结果与实验的频率结果对比如表4所示。

表3 三维四向编织复合材料的弹性性能[17]

图11 阵型位移云图 (a)一阶弯曲阵型；(b)二阶弯曲阵型Fig.11 Cloud pictures of mode shape displacements (a)first bending mode shape;(b)second bending mode shape

No．Naturalfrequency/HzFirstorderSecondorderV3-278．431646．00V3290．151773．00V3+301．331781．20

在有限元计算时不仅可以得到弯曲阵型，还可以得到扭转阵型。但因本工作只研究弯曲振动，所以只选取了有限元计算中弯曲振动的结果来研究。由于理论计算中采用的T型梁细观结构参数与实验中的并不相同，不过表面编织角大体一致，所以在计算中选取了两种纤维体积分数，以更准确地估计实际中T型梁的固有频率。图11为有限元模态计算得到的T型梁的第一阶和第二阶弯曲阵型。与实验模态分析得到的第一阶和第二阶阵型相比，有限元模拟得到的弯曲阵型更加生动形象、直观，并可以观察到T型梁上任意点的位移变化。但实验得到的弯曲阵型和有限元计算得到的弯曲阵型的振动方式是一致的。此外，与阵型对应的实验测量和有限元计算的固有频率也具有较好的一致性。

表4中V3是实验测量的固有频率，V3-，V3+是采用文献[17]的数据计算的结果，其纤维体积分数的关系是V3-< V3< V3+。通过对比，可以看出任意阶实验得到的固有频率都介于计算得到的两个固有频率之间，且与它们之间的差值百分比最大不超过8%，所以若理论计算中采用的T型梁细观结构参数与实验中的相同，其差值百分比也必然不超过8%，故实验得到的固有频率结果是合理的。此外，从实验与计算结果的一致性还可以得出对于三维四向编织的复杂结构，可以通过有限元计算来大致地预测其振动的固有频率。

4 结论

(1)表面编织角相同时，三维四向编织结构的碳纤维/环氧树脂复合材料T型梁的固有频率随纤维体积分数的增加而增大，阻尼性能随纤维体积分数的增加而降低。

(2)由于三维四向编织结构的碳纤维/环氧树脂复合材料T型梁的抗激振性能随着纤维体积分数的增加而增大，减振性能随着纤维体积分数的增加而减小，所以在实际应用中应综合考虑，合理地选择其纤维体积分数。

(3)通过观察三维四向编织结构的碳纤维/环氧树脂复合材料T型梁的阵型可以准确地判断其固有频率的阶数。

(4)可以利用有限元计算来大致地预测三维四向编织结构的碳纤维/环氧树脂复合材料T型梁或者其他复杂结构的振动固有频率。

[1] 陈光伟,陈利,李嘉禄,等. 三维多向编织复合材料T型梁抗弯应力分析[J]. 纺织学报,2009,30(8):54-58.

CHEN Guang-wei, CHEN Li, LI Jia-lu, et al. Study on flexural stress of T beam of 3-D multidirectional braided composites[J].Journal of Textile Research,2009,30(8):54-58. [2] 李典森,卢子兴,李嘉禄,等. 三维编织T300/环氧复合材料的弯曲性能及破坏机理[J]. 航空材料学报,2009,29(5):82-87.

LI Dian-sen, LU Zi-xing, LI Jia-lu,et al. Bending properties and failure mechanism of three dimensional T300/epoxy braided composites[J].Journal of Aeronautical Materials, 2009,29(5):82-87.

[3] 蔡敢为,钟掘,廖道训. 三维编织复合材料构件的机构模态阻尼[J]. 中国机械工程,2000,11(5):481-484.

CAI Gan-wei, ZHONG Jue, LIAO Dao-xun. Modal damping of mechanisms fabricated from three-dimensional braided composite[J].China Mechanical Engineering,2000,11(5): 481-484.

[4] 李典森,卢子兴,李嘉禄,等. 三维编织复合材料振动阻尼特性的实验研究[J]. 机械强度,2009,31(2):211-214.

LI Dian-sen, LU Zi-xing, LI Jia-lu, et al. Experimental research on the vibration damping properties of 3D braided composites[J].Journal of Mechanical Strength,2009,31(2):211-214.

[5] 孙雨果,严实,梁红. 新型三维编织复合材料等网格结构力学性能分析[J]. 宇航学报,2007,28(4): 827-830.

SUN Yu-guo, YAN Shi, LIANG Hong. The mechanical behavior study of a new type of 3D braided composites iso-lattice truss[J]. Journal of Astronautics, 2007,28(4): 827-830.

[6] 裴晓园,李嘉禄,何玉强. 纤维体积分数对炭纤维三维四向编织复合材料实验模态性能的影响[J]. 固体火箭技术,2012,35(2):267-270.

PEI Xiao-yuan, LI Jia-lu, HE Yu-qiang. Effects of fiber volume fraction on experiment modal behavior of three-dimension and four-direction braiding composites[J].Journal of Solid Rocket Technology,2012,35(2):267-270.

[7] 裴晓园,李嘉禄,何玉强. 纤维取向对三维四向编织复合材料与层合复合材料振动性能的影响[J]. 材料工程,2013,(7):16-23.

PEI Xiao-yuan, LI Jia-lu, HE Yu-qiang. Effects of fiber orientation on modal experimental analysis of three-dimension and four-direction braided composites and laminated composites[J]. Journal of Materials Engineering,2013,(7):16-23.

[8] GAO Y, LI J L. Effects of braiding angle on modal experimental analysis of three-dimensional and five-directional braided composites[J]. Composites: Part B,2012,43(5):2423-2428.

[9] OOIJEVAAR T H, LOENDERSLOOT R, WARNET L L,et al. Vibration based structural health monitoring of a composite T-beam[J].Composite Structures,2010,92(9):2007-2015.

[10] HERMAN A P, ORIFICI A C, MOURITZ A P. Vibration modal analysis of defects in composite T-stiffened panels[J].Composite Structures,2013,104(10):34-42.

[11] LEE J, KIM S E. Free vibration of thin-walled composite beams with I-shaped cross-sections[J].Composite Structures,2002,55(2):205-215.

[12] THINH T I, QUOC T H. Finite element modeling and experimental study on bending and vibration of laminated stiffened glass fiber/polyester composite plates[J].Computational Materials Science, 2010,49(4):S383-S389.

[13] ALNEFAIE K. Finite element modeling of composite plates with internal delamination[J].Composite Structures,2009,90(1):21-27.

[14] 郑丽娟,赵玉涛,金明江,等. 纤维/树脂/铝合金叠层复合材料的显微组织与阻尼性能[J]. 中国有色金属学报,2003,13(3):667-670.

ZHENG Li-juan, ZHAO Yu-tao, JIN Ming-jiang, et al. Microstructure and damping property of fiber/resin/aluminum alloy laminated composite[J].The Chinese Journal of Nonferrous Metals,2003,13(3):667-670.

[15] 余建新,陈立平. 复合材料结构阻尼测试分析[J]. 哈尔滨商业大学学报:自然科学版,2011,27(5): 729-732.

YU Jian-xin, CHEN Li-ping. Analysis on composite structural damping measurement[J].Journal of Harbin University of Commerce: Natural Sciences Edition,2011,27(5): 729-732.

[16] KHAN S U, LI C Y, SIDDIQUI N A. Vibration damping characteristics of carbon fiber-reinforced composites containing multi-walled carbon nanotubes[J].Composites Science and Technology,2011,71(12):1486-1494.

[17] 李典森,卢子兴,蔺晓明,等. 三维四向编织复合材料弹性性能的有限元预报[J]. 北京航空航天大学学报,2006,32(7):828-832.

LI Dian-sen, LU Zi-xing, LIN Xiao-ming, et al. Finite element prediction of elastic properties of three dimensional and four directional braided composites[J].Journal of Beijing University of Aeronautics and Astronautics,2006,32(7):828-832.

Effect of Fiber Volume Fraction on Modal Properties of Three-dimension Braided Composite T-beams

WANG Huan,LI Jia-lu,FAN Wei

(Tianjin and Ministry of Education Key Laboratory of Advanced Textile Composite Materials,Institute of Composite Materials, Tianjin Polytechnic University,Tianjin 300387,China)

The modal properties of carbon fiber three-dimension and four-direction braided composite T-beams with different fiber volume fractions were studied by the free vibration method of cantilever beams. The effect of fiber volume fraction on natural frequency and damping was analyzed. The measured and finite element calculated results of natural frequency were compared. The results show that the modal properties of T-beams have nothing to do with the position of excitation point. The natural frequency of the composite T-beams increases and damping properties of the composite T-beams decrease with the increasing of fiber volume fraction. The order of the natural frequency of T-beam could be estimated accurately by the mode shape. The measured results are in agreement with the calculated results.

three-dimension and four-direction braiding;composite T-beam;modal analysis

10.11868/j.issn.1001-4381.2015.09.013

TB332

A

1001-4381(2015)09-0080-07

天津市科技计划项目(11ZCKFSF00500,10SYSYJC27800)

2014-05-15；

2015-03-21

李嘉禄(1947-)，男，教授，主要从事纺织复合材料结构及性能的研究，联系地址：天津市西青区宾水西道399号天津工业大学复合材料研究所(300387)，E-mail：lijialu@tjpu.edu.cn