基于主成分分析法的公路客运量预测模型分析
谭逸萍
(长安大学汽车学院,陕西 西安 71000)
基于主成分分析法的公路客运量预测模型分析
谭逸萍
(长安大学汽车学院,陕西西安71000)
谭逸萍(1990—),女,工学硕士,研究方向:汽车工程。
摘要:文章基于主成分分析的基本理论与模型,采用SPSS 软件,对影响四川省公路客运量的相关因素进行主成分分析,克服多重共线性的问题,构建出四川省公路客运量预测模型。根据预测结果显示,该模型具有较高的精度,适用于影响因素指标较为明确的短期客运量预测,能够满足四川省目前公路客运量预测的需要,对四川地区的公路旅客运输发展也有着一定的指导作用,具有一定的科学性与有效性。
关键词:主成分分析;多重共线性;公路客运量;预测;模型分析
0引言
公路运输是国民经济的基础性、服务性产业,公路运输的发展关系到我国经济社会发展的全局[1]。近年来,随着公路运输的快速发展,公路客运量已经成为衡量公路运输发展水平的重要指标,同时也在很大程度上反映当今社会经济的发展现状和人民的生活水平。公路客运量预测是交通运输规划的基础,其预测质量的好坏不仅会影响交通运输规划与社会经济发展的适应性,也在一定程度上影响交通运输设施的投资与运营效益[2]。影响公路客运量的因素主要有社会经济发展水平、经济结构、人口数量、城镇化水平、人民物质文化生活水平、产业布局、交通运输网络拓展程度等[3]。目前客运量的预测主要有定性与定量两种预测方法[4]。定性预测主要有专家预测法、德尔菲法、类推法等,定量预测法包括回归分析法、指数平滑法、弹性系数法、灰色预测等。但在这些预测方法中,由于影响因素过多,导致很多因素都存在较高的相关性,即通常的多重共线性,从而出现回归系数不能通过显著性检验,甚至有的回归系数所带符号与实际意义不符[5],大大降低了预测模型的精度,本文在以前预测方法的基础上,简单介绍了主成分分析的基本理论,并通过SPSS统计软件,根据2003-2012年四川省各市的指标数据,精确选取影响公路客运量的各个因素,并分别对各个因素进行主成分分析,克服多重共线性的问题,从而建立四川省公路客运量的预测模型,提高预测精度。
1主成分分析的基本理论及模型
1.1 主成分分析基本理论
主成分分析是对多个变量因素进行线性变换,以选出较少个数的重要变量的一种多元统计分析方法,又称为主量分析。主成分分析是一种数学降维的思想,找出几个综合的变量即主成分来代替原来的众多变量的信息量,而且各综合变量之间互不相关[6]。每个主成分都包含原来变量的绝大部分信息,且这些信息都互不重叠。
主成分分析的原理是将原来众多的具有一定相关性的变量重新组合成新的且不相关的综合变量。将选取的第一个线性组合即第一个综合变量(设共有n个指标)记为Z1,协方差为Var(Z1),主成分分析是通过线性组合的协方差来表达的,因此主成分分析仅取决于变量的协方差矩阵[7]。协方差越大,则第一个主成分Z1包含的信息便越多,在所有的线性组合中,Z1的协方差是最大的。如果第一个主成分不足以代表原来n个变量的信息,那么再考虑选取第二个主成分,为了有效反映原来的信息,F1已有的信息不需要出现在F2中,即COV(Z1,Z2)=0。从而依次类推得到第3、4、5…n个主成分[6]。
1.2 主成分分析模型
对于一个样本资料,观察n个变量x1,x2,…xn,m个样本的数据资料阵为:
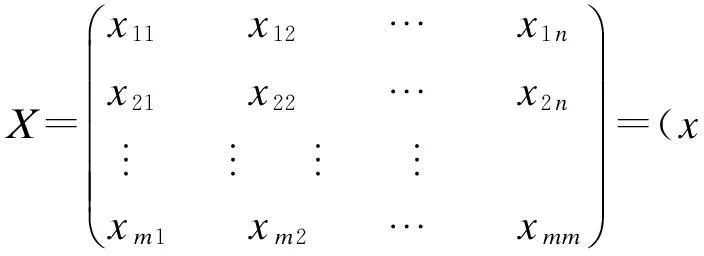
主成分分析就是将n个观测变量综合成为n个新的变量(综合变量),即:
简写为:Zj=αj1x1+αj2x2+…+αjnxn

j=1,2,…n
主成分分析法的模型应满足以下条件:
(1)Zi,Zj互不相关(i≠j,i,j=1,2…n)
(2)Z1的方差大于Z2的方差,Z2的方差大于Z3的方差,依次类推[6]。
(3)ak12+ak22+…+akn2=1,k=1,2,…n
于是,称Z1为第一主成分,Z2为第二主成分,依次类推,一共有n个主成分。an为主成分系数,则上述模型用矩阵表示为Z=AX,其中:


A成为主成分系数矩阵。
通过主成分分析建立预测模型的主要步骤如下:
(1)选取与选题相关的指标和数据;
(2)对指标数据进行标准化处理;
(3)建立协方差矩阵,对指标之间的相关性进行判断;
(4)根据协方差矩阵求出特征值、主成分贡献率和累积贡献率,从而确定主成分个数;
(5)建立初始因子载荷矩阵,解释主成分Zj;
(6)建立并求解主成分回归模型。
2影响四川省公路客运量的因素
随着近年来四川省公路客运的快速发展,很多因素都会直接影响到公路客运量,综合各个因素的影响程度,本文主要选取了四个方面的影响因素:社会经济结构、经济发展水平、居民收入与消费、运输设施建设水平。认真分析这些影响因素,消除因素之间的共线性,选取最适合的指标建立四川省公路客运量预测模型,对提高客运量的预测精度有着十分重要的意义。

图1 影响公路客运量的因素图
公路客运量在很大程度上受到经济发展水平的影响,人口数量、地区的生产总值的变化都会使客运量发生相应的变化。而居民收入与消费水平在很大程度上反映了城镇居民的消费与购买能力,与交通出行之间有着一定的联系[8]。运输设施的建设水平在很大程度上反映了道路运输行业的发展状况。本文中所选取的影响四川省客运量的具体影响因素如图1所示。
3实例分析
3.1 指标的选取及标准化
通过SPSS回归分析多个指标,最终确定选取地区生产总值(X1)、社会消费品零售总额(X2)、旅游人数(X3)、公路总里程(X4)、农村家庭人均纯收入(X5)、公路营运载客汽车拥有量(X6)、第二产业比重(X7)、高速公路总里程(X8)、人均地区生产总值(X9)九个相关指标进行主成分分析,在保留大部分原信息的前提下,对这些变量进行简化分析,转化为不相关的少数变量,综合这些变量建立回归模型。
本文采用四川省2003-2012年的统计年鉴数据进行分析[9],根据统计年鉴所查数据,四川省各年的具体指标值如表1中所示。Y表示年公路客运量。采用SPSS软件对指标进行标准化处理,表2为相关系数矩阵,由表2中可以看出各指标的相关系数均>0.5,因此这些指标可以用来进行预测,模型是准确的。

表1 2003-2012年四川省相关指标值表

表2 相关系数矩阵表
3.2 多重共线性诊断
由相关性系数矩阵表(见表2)可以看出自变量数目众多,且变量之间存在明显的相关性,因此在建立模型时会存在严重的多重共性问题。为了验证是否存在多重共线性的问题,先通过SPSS软件建立因变量与自变量的多元线性回归模型[10]。
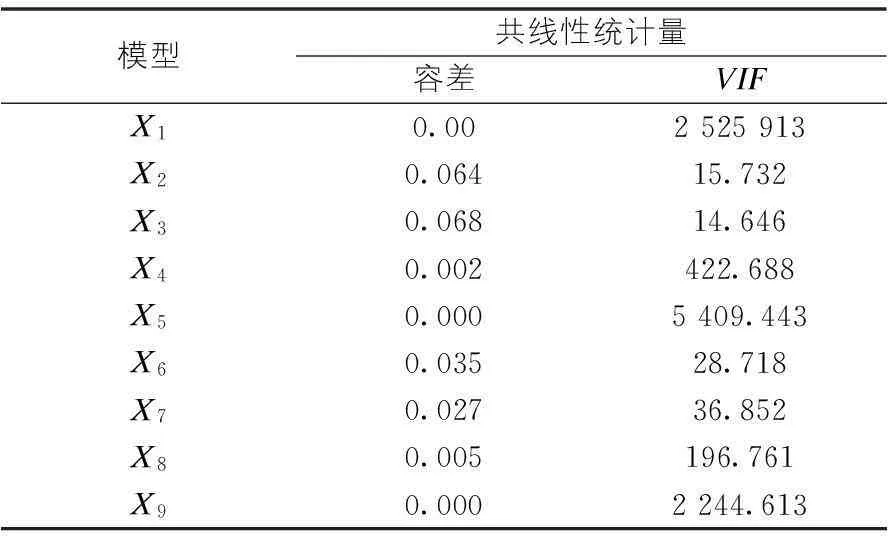
表3 多重共线性诊断表
通过SPSS软件进行回归分析检验多重共性,选取容差和各自变量的方差扩大因子为多重共线性统计量,由诊断结果(见表3)可以明显看出,所有自变量的方差扩大因子均>10,容差均<0.1。说明各自变量之间存在严重的多重共线性,这样在很大程度上影响预测精度,因此应采用主成分分析法对其进行简化分析,将原来众多的彼此相关的指标变量转化为一组新的互不相关的指标变量,并再一次通过回归分析,建立公路客运量预测模型,进行科学准确的预测。
3.3 模型建立与求解
通过SPSS软件对现有自变量X1,X2,…X9进行主成分分析,得到总方差解释表(见下页表4)。由表4中可以看到提取的两个主成分的特征值均>1,第一主成分的特征值为6.992,方差为77.693%;第二主成分的特征值为1.018,方差为11.314%。前两个主成分的累积贡献率>85%,达到了89.007%,这说明前两个主成分已经反映了原来九个变量的89.007%的信息,原有的9个变量可以简化为这两个主成分进行简化分析。图2为碎石图,从图中可以看出,从第三个主成分开始,特征值已经趋于平稳,因此第二个主成分是合理的,则选取前两个主成分建立预测模型即可。
表5为初始因子载荷矩阵,即成分矩阵,从表中可以看出地区生产总值(X1)、旅游人数(X3)、公路总里程(X4)、农村家庭人均纯收入(X5)、公路营运载客汽车拥有量(X6)、第二产业比重(X7)、高速公路总里程(X8)、人均地区生产总值(X9)在第一主成分上有很高的载荷,社会消费品零售总额(X2)、在第二主成分上占有很高的载荷,因此两个主成分基本可以反映这9个变量的全部信息,从而可以用这两个新变量代替以前的相关变量。
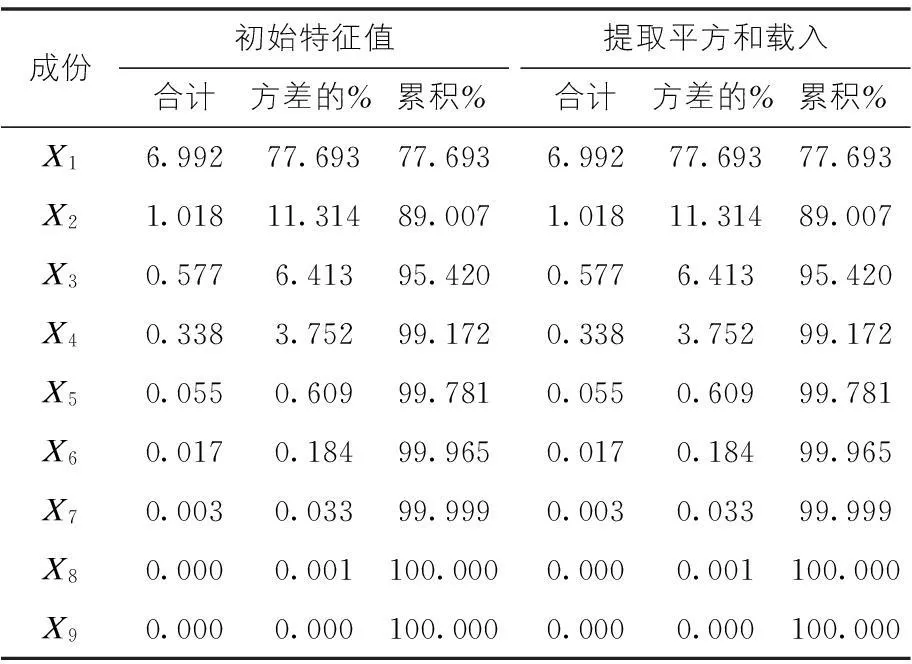
表4 总方差解释表

表5 初始因子载荷矩阵表
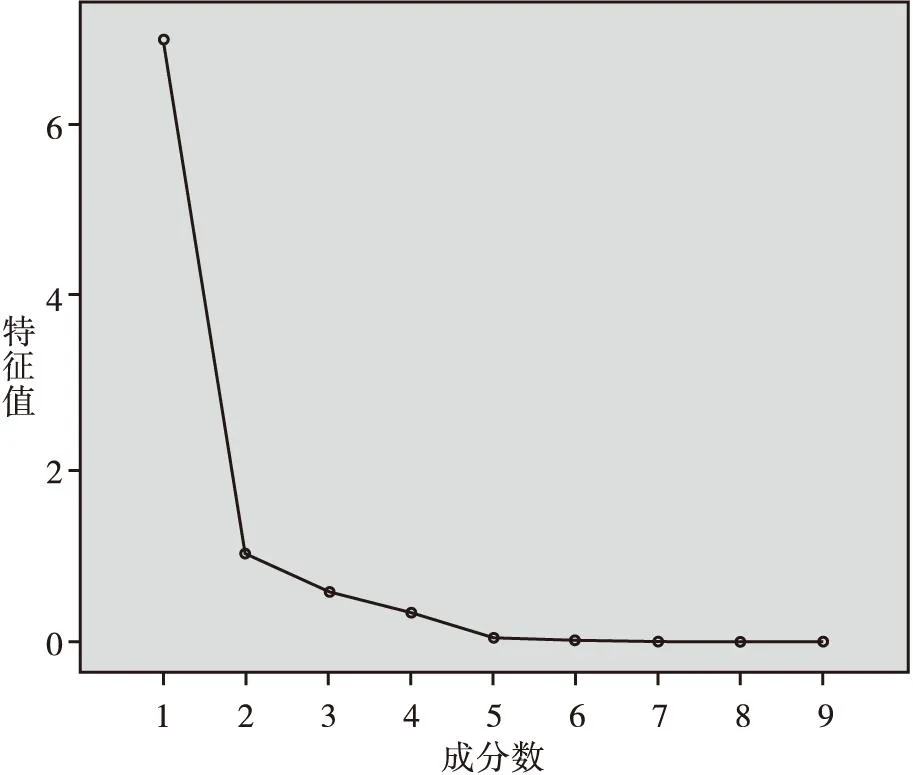
图2 碎石图
然而只通过因子载荷矩阵还不能得出主成分的表达式,还需要把初始因子载荷中的每列系数除以相应主成分的特征根的平方根后才能得到主成分的系数向量。将标准化之后的数据与得到的特征向量相乘,可以得到主成分表达式[11]。特征向量为:
Z1=0.37*ZX1+0.22*ZX2+0.27*ZX3+0.37*ZX4+0.37*ZX5+0.29*ZX6+0.37*ZX7+0.34*ZX8+0.347ZX9
Z2=-0.16*ZX1+0.69*ZX2+0.25*ZX3+0.09*ZX4+0.18*ZX5+0.51*ZX6+0.08*ZX7+0.32*ZX8+0.17ZX9
以标准化之后的ZY为因变量,将Z1、Z2得到的评价值与ZY做多元线性线性回归分析,得到回归模型为:
ZY=0.376Z1+0.007Z2
(1)
得到标准误差估计如表6所示,其为0.996,调整后的R2为0.994,标准估计误差为0.076,说明该模型的总体拟合效果是良好的,并且该回归模型能够通过F检验与t检验,在统计学中是具有意义的,能够对客运量做出合理的预测。

表6 回归模型误差分析表
由于提取的两个主成分与原始的自变量X1,X2,…X9存在着线性关系,经过相关转换,用X1,X2,…X9代替主成分Z1与Z2,得到因变量Y(四川省公路客运量)与原始变量X1,X2,…X9的线性回归方程:Y=0.92*X1+1.513*X2+7 725.52*X3+815.95*X4+3.65*X5+3 684.43*X6+141 436.11*X7+63 712.18*X8+0.74*X9+32 899.82
3.4 模型的检验
分别将2003-2012年各年四川省的相关指标数据(即X1,X2,…X9)代入主成分回归模型中,可以求得各年的公路客运量预测值,并将预测值与实际值进行比较,如图3所示,主成分回归模型得到的预测值与实际值的拟合较好,最高误差仅为3.04%,10年的平均误差为1.08%,基本上能够满足公路客运量的预测需要。
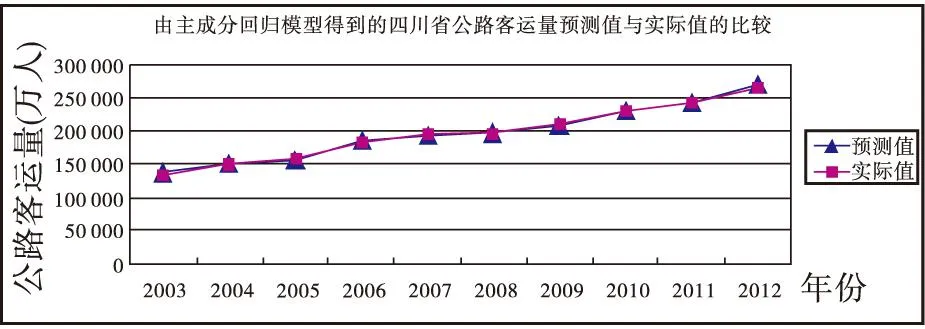
图3 由主成分回归模型得到的四川省公路客运量预测值与实际值比较图
4结语
从文中的实例可以看到影响公路客运量的因素是众多的,全面准确地把握这些影响因素对公路客运量的预测十分关键。但由于众因素的较大多重共线性,直接采用多元回归分析已经不具有较大的意义,主成分回归分析将多个相关变量转化为互不相关的变量的优点在对公路客运量的预测中具有一定的应用价值。
本文在对四川省公路客运量的预测中,考虑了影响客运量的诸多因素,因此预测精度较高,但是由于各时期的变量因素会发生变化,预测模型也会相应发生变化,因此主成分回归模型适用于因素指标发展较为明确的短期预测。
参考文献
[1]交通部综合规划司.国家公路运输枢纽布局规划[R].北京:中华人民共和国交通部,2007.
[2]马银波.公路运量长期预测的质量与模型[J].西安交通大学学报,2000(20):74-77.
[3]姚新胜,苏延升,孙金玲.公路客运短期运量预测研究[J].公路交通科技,2005,22(11):155-188.
[4]陆化普.交通规划理论与方法[M].北京:清华大学出版社,1998.
[5]贾元华,敖谷昌,等.基于主成分回归的公路客运量预测模型研究[J].交通标准化,2009(9):106.
[6]朱星宇,陈勇强.SPSS多元统计分析方法及应用[M].北京:清华大学出版社,2011.
[7]Gao Haibo,Hong Wenxue,Cui Jianxin,etc.Optimization of Principal Component Analysis in Feature Extration[C]Harbin Proceedings of the 2007 IEEE in ternational conference on Mecha-tronice and Automation,2007(8):3128-3132.
[8]李为博.华东六省公路客运量预测研究[J].交通与运输,2013(1):69-72.
[9]四川省统计局.四川统计年鉴-2012[M].北京:中国统计出版社,2012.
[10]高王翠,单飞,杨宇翔.基于SPSS主成分分析法在公路客运量预测中的应用[J].山东交通科技,2011(2):9-12,20.
[11]张文霖.主成分分析在SPSS中的操作应用[J].市场研究,2012.12:32-35.
Analysis of Highway Passenger Volume Forecasting Model based on Princi-pal Component Analysis Method
TAN Yi-ping
(School of Automobile,Chang’an University,Xi’an,Shaanxi,71000)
Abstract:Based on the basic theories and models of principal component analysis,and by using SPSS software,this article conducted the principal component analysis on relevant factors affecting the Si-chuan highway passenger volume,overcame the multicollinearity problem,and built the forecasting model of Sichuan highway passenger volume.According to the forecast results,this model has higher accuracy,suitable for the short-term passenger volume forecast with clearer influencing factors and index,it can meet the current highway passenger volume forecast needs in Sichuan,and it has some guiding role for highway passenger transport development in Sichuan region and is scientific and ef-fective.
Key Words:Principal component analysis;Multicollinearity;Highway passenger volume;Forecasting;Model analysis
收稿日期:2015-02-08
文章编号:1673-4874(2015)02-0078-06
中图分类号:U492.4+13
文献标识码:A
DOI:10.13282/j.cnki.wccst.2015.02.020
作者简介

