三维网格模型数字水印算法改进研究

李淑敬，李林国

（阜阳师范学院　信息工程学院，安徽　阜阳　236041）

三维网格模型数字水印算法改进研究

李淑敬，李林国

（阜阳师范学院信息工程学院，安徽阜阳236041）

摘要：数字水印技术可以有效地保护数字产品知识版权，跟踪打击盗版行为，证明产品真伪，随着三维数据在信息领域的快速发展，研究数字水印技术前景广阔.本文在数字水印研究现状的基础上，参考图像数字水印技术，对三维网格模型数字水印系统在改进算法及实现方面进行了研究.

关键词：数字水印；三维网格模型；水印算法；改进

项目来源：阜阳师范学院教研一般项目

数字水印就是在数字图像、音频或视频等数字产品中嵌入秘密信息，借此来加强对数字产品知识版权在保护.包括图像水印、视频水印和三维模型水印三个类别.随着科技的发展及计算机技术的进步，相关专家学者对数字水印的技术研究也进一步深入，相继产生了网格模型、点云模型及参数曲面三种三维模型水印算法.在此基础上，本文主要对三维网格模型数字水印算法改进进行了研究.

1　三维模型水印原理

首先设计3D模型和密匙，然后在数字产品中嵌入水印.水印嵌入前对水印数据进行定义，利用算法通过媒介发送并生成3D模型，形成对数字产品知识版权的保护.打开该数字产品需要借助密匙对水印算法进行检测，进而提取水印信息，恢复3D模型.三维模型水印嵌入与提取过程如下图所示（图1）.

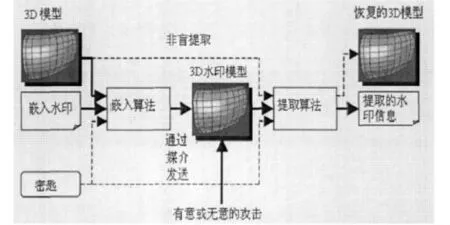
图1三维模型水印嵌入与提取过程

三维模型具有如下特点：首先是定点排列的无序性.图像以扫描线顺序排列，音频和视频按照时间先后顺序排列，而CAD图形数据则没有固定的数据顺序；其次是缺少自然的参数化分解方法.缺少视域分析所需要的参数化分解方法，所以不能直接运用数学工具进行分解操作；然后是表示方法不唯一.同一个三维模型，可以有不同的模型表现形式.但是，隐蔽性与鲁棒性是三维模型数字水印需要最优先考虑的基本条件.

2三维网格模型数字水印简析

三维网格模型是数字水印的最基础形式，是进行研究其他三维模型数字水印技术的基础.三维网格水印算法分为盲水印及非盲水印两种形式：三维网格盲水印算法在水印提取时不需要原始模型信息，按照工作域可以分为空域算法和视域算法；非盲水印算法提取水印需要提供原始模型信息，同时还需要进行重对齐、采样等一系列预处理.对于具体的相关算法，由于各类科普文章都有所涉及，这里就不在一一列举了.

3三维网格模型数字水印改进算法

根据资料查阅发现，一般三维模型数字水印算法与图像数字水印算法基本类似，都是在空域操作实现的.相同点就是对模型定点坐标进行直接或间接的修改来嵌入水印.这样计算量减小了，但鲁棒性却不高.针对这样的问题，要增强对几何攻击的能力，就要提高鲁棒性，进行变换域算法操作.

3.1算法改进原理

不需要对三维模型进行重定位，只要在嵌入水印前对其进行转变到一个仿射不变空间的预处理即可.计算复杂且耗时的重定位处理就可以避免了.

假设三维模型由一个定点集合为V｛Vi}及其连接的关系集合C组成，那么每个顶点Vi都会具有三维坐标如：V1=（Xi，yi，Zi）.接下来使其转换到一个不变仿射空间，使其具备旋转和尺度变换，但平移性恒定.具体操作过程为：

A.先将所有质心计算出.方式为：

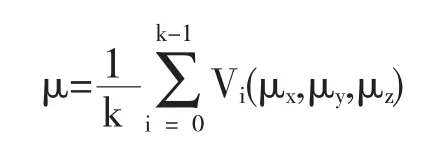
B.通过原三维模型定点Vi减掉质心值使模型平移.方式为：

Vi'=（xi'，yi'，zi')=（xi-μx，yi-μy，zi-μz)

C.要保证变换后的三维模型的平移性恒定，需要再进行主成份计算.T为顶点主要成分的特征矢量，通过顶点对应坐标协方差距阵求其最大值，使其与Z轴重合.协方差距阵方式为：

3.2嵌入水印过程

（1）首先将嵌入水印信息（或密匙）输入伪随机序列发生器并生成相对应的二进制序列（水印信息（或密匙）用K表示；水印序列长度用Nw表示；水印生成算法用Wi和G表示）.则其序列为：

W={wl，l=0，1，…，Nw-1}，W=G（K)

（2）其次将顶点坐标（X1，y1，Z1）在网格顶点排成一维顶点序列时换成对应的θi，øi，ri值，其对应关系如图3所示：

图3 x.y.z与θ.φ.r关系图

求θi，øi，ri值的公式为：

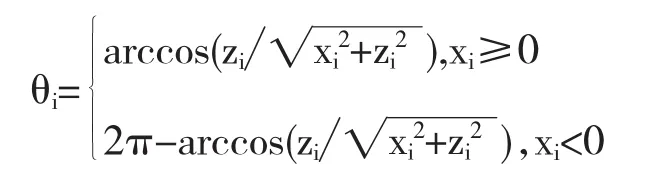
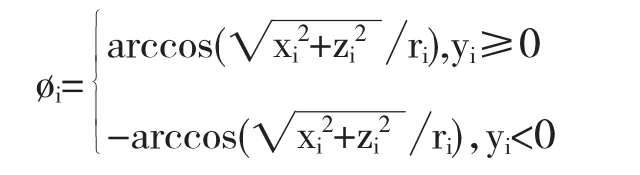
（3）求出ri值并归一化顺序排列，嵌入水印对象设为R={ri}.

（4）按顺序将R={ri}分为S×Nw个元素（Nw个组，每组S个元素）.则R=｛ril}.其中，i=0...Nw-1；l=0. ...S-1.ril作为嵌入单元进行水印信息嵌入.过程如下：

先将单元ril进行DFT变换，得到DFT的对应系数Rlf，将一位水印信息Wl嵌入其中，公式如下：

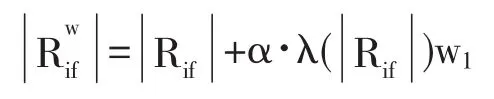
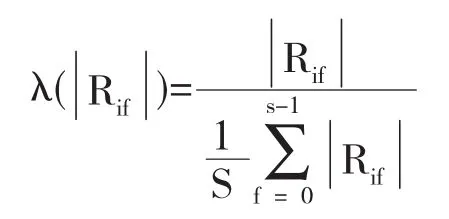
其中将Rwif进行IDET即可得到含有水印信息的rw1j，对其进行逆序得到rwi.由此可求得水印中间过渡顶点坐标.即：Xi'=riw×cosøi×sinθi.yi'=riw×sinθi. zi'=riw×cosøi×cosθi.对过渡顶点坐标进行预处理的逆变换，即可得到最终嵌入水印顶点.

3.3水印提取

针对一些攻击会改变原始网格，加之重采样算法复杂耗时，本文介绍一种简单可行易操作的算法：将上面嵌入水印的顺序倒过来重新操作，通过计算相关性系数Cor来对水印鲁棒性进行评价衡量.相关性系数Cor通过下式求得：

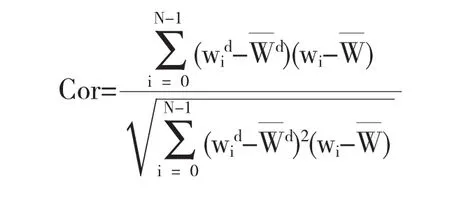
上式中Wd为提取出来的水印序列，W是原始水印序列是Wd序列各位的平均值是W序列各位的平均值，N是水印序列长度.

如果提取出的水印与原始网格模型嵌入者所出示的水印的相关值大于所设定的阀值，则可证明嵌入者拥有版权.反正则不能证明.

3.4实验结果

为了对本算法的可取性进行验证，通过具体的3D图像进行了测试.实验模型有顶点1571个，三角面2999个.实验中生成的原始水印序列长度为32，每一组定点数为48.分别通过简化攻击、噪声攻击及剪切攻击的测试对算法的鲁棒性进行了检验.

在进行简化攻击测试时，对嵌有水印的3D图像采用了StanMelax的算法进行了简化，结果是顶点在受攻击模型中虽然所剩不多，但其鲁棒性在本算法中依然表现很强.（见表1）

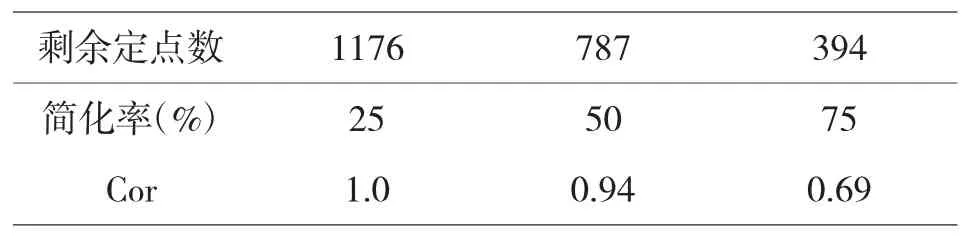
表1简化攻击实验结果

在进行噪声攻击实验时，将均匀随机噪音加入已加水印模型的顶点坐标，将噪声矢量加入嵌入水印后的逐个顶点.取噪声向量的长度与网格顶点与中心的距离比值为噪声幅度.结果显示，本算法在噪声攻击下仍有较强的鲁棒性.（见表2）

表2噪声攻击实验结果

在进行剪切攻击实验时，剪切百分比分别为原实验模型的90%，60%，30%和10%，结果显示良好.（见表3）

表3

4小结

本文在分析三维网格模型数字水印常见算法的基础上，提出了一种新的改进算法，对三维网格模型数字水印系统进行了补充与完善.探索发现无止境，没有最好，只要更好，希望以此能加强对3D数字产品版权的有效保护.

——

参考文献：

〔1〕陈丽萍，孔祥增，姚志强.基于几何特征的三维模型双重数字水印算法[J].计算机系统应用，2011（08）.

〔2〕王新宇，詹永照.结合顶点趋势检测的三维模型数字水印算法[J].计算机应用，2011（10）.

〔3〕冯小青，潘志庚，李黎.面向3D网格模型的多重数字水印算法[J].计算机辅助设计与图形学学报，2010（01）.

〔4〕李军.三维模型数字水印研究[J].湖北民族学院学报(自然科学版)，2009（01）.

基金项目：安徽省高等学校省级优秀青年人才基金重点资助项目，项目名称：三维网格模型盲水印技术研究（2013SQRL102ZD）项目名称：面向软件开发能力培养的《软件工程》课程教学模式研究与实践（2014JYXM41）

中图分类号：TP309.7

文献标识码：A

文章编号：1673-260X（2015）07-0025-03