基于MATLAB的非线性曲线拟合方法及应用

王方方

（兰州商学院，甘肃　兰州　730020）

基于MATLAB的非线性曲线拟合方法及应用

王方方

（兰州商学院，甘肃兰州730020）

摘要：本文选取了上海市的居民消费水平为自变量，全市财政收入为因变量，编程对因变量和自变量进行指数模型和二次模型的非线性拟合，分别得出y=0.0021e1.4737x和y=0.0973x+64.2873两个模型.又选取了上海市的居民消费水平为自变量，居民消费价格指数为因变量，编程对因变量和自变量进行Logistic函数和双曲线函数模型的非线性拟合，分别得出y=和两个模型的函数方程.运用MATLAB软件对因变量和自变量进行这些非线性曲线模型拟合，得出函数方程.

关键词：非线性曲线拟合；MATLAB；对数曲线；Logistic曲线

1　引言

在生产和科学实验中，很多现象往往不是线性关系，而是呈现某种非线性曲线关系，所以就产生非线性模型理论.非线性曲线拟合是一个重要的且常用的方法，可以根据有关数据得到相应的实验曲线和图形解决要解决的问题.非线性模型存在着复杂和多样的形式，选择模拟合适的模型要基于实际数据.可以参照两种方法：首先，要确定基于所述散点图的类型，也就是，从散点图的形状确认模型类型;第二是基于一定的经济背景知识[1].在MATLAB软件中，非线性拟合主要是通过函数inline和命令[beta，r，J]=nlinfit（X，Y，fun，beta0).来进行的.其中，函数inline是用来定义所要求的函数的；用命令

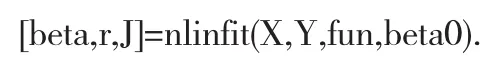
来进行拟合，其中X，Y为原始数据，fun是在M文件中定义的函数，是函数中参数的初始值，beta0是函数中参数的初始值：beta为参数[2].

曲线拟合是一种连续曲线近似地描述或者近似的曲线拟合平面上离散点所表示的坐标之间的关系的数据处理方法用.用解析表达式离散数据的近似方法.在科学实验或社会活动，通过实验或观察获得的一组数据量x与y的一对数据组（xi，yi)（i=1，2，…，m)，其中每个xi彼此不同.人们希望能够使用一种解析表达式来表示数据背景材料规律，该表达式y=f（x，c)反映x和y之间的依赖关系，也就是，在一定意义上，“最佳”近似或拟合已知的数据.通常f（x，c)被称为拟合模型，其中c=（c1，c2，…，cn)是一些未知参数.当c在f中线性出现时就称为线性模型，否则被称为非线性模型.有适合的曲线拟合的标准偏差许多优良的措施中，最常见的方法是，选择参数c使得拟合模型与实际观测为在曲线的每点拟合的残差（或偏差）.

有很多求解方法可以求解拟合曲线，线性模型可以通过建立并求解方程组确定需要的参数，进而求得拟合曲线.而对于非线性模型，直接建立模型求解出方程组确定参数是得不到需要的拟合曲线，需要用最优化方法求得所需的参数（称为非线性最小二乘拟合）或者是根据非线性方程组得到拟合曲线，得到需要的参数得到拟合曲线.

非线性曲线拟合的应用非常广泛，李玉星等就对ISAR成像中的频率进行了非曲线拟合.非线性曲线拟合的方法也有许多，严晓明和郑之利用BP神经网络和RBF人工神经网对非线性函数进行MATLAB仿真.韩吉德等采用非线性TLS拟合的方法.处理非线性曲线拟合的软件有MATLAB、LINGO等.应六英为了解决MATLAB中调用nlifit函数和lsqcurvefit函数时存在的问题和困难，运用LINGO正好弥补了MATLAB处理非线性曲线拟合的不足.陈岚峰等就是用MATLAB进行最小二乘法曲线拟合，同时唐家德等也是采用MATLABA的非曲线拟合.

2 MATLAB曲线拟合的基本理论

2.1 MATLAB曲线拟合的基本原理

设有实验数据（xi，yi)，（i=1，2，…，n)，寻找函数f（x，θ)，使得函数在点xi，i=1，2，…处的函数值与观测数据偏差的平方和达到最小.即求满足如下条件f（x，θ赞)的函数，使得

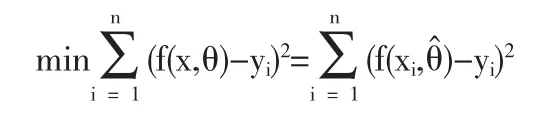
其中θ是待定的参数，而θ赞就是最小二乘法所确定的最佳参数.

2.2 MATLAB中实现非线性回归的命令

（1)非线性拟合命令为nlinfit，其调用格式为：

[beta，r，J]=nlinfit（x，y，fun，beta0)

其中，x，y为原始数据，fun是在M文件中定义的函数，beta0是函数中参数的初始值；beta为参数的最优值，r是各点处的拟合残差，J为雅克比矩阵的数值.通常，可以利用inline定义fun函数，方法如下：

fun=inline（‘f（x)'，‘参变量'，‘x'

（2）非线性回归预测命令为nlpredci，其调用格式为：

fun=inline（‘f（x)'，‘参变量'，‘x'

其中，输入参数beta，r，J是非线性拟合命令nlinfit的输出结果，fun是拟合函数，inputs是需预测的自变量；输出量ypred是inputs的预测值.

（3）非线性回归置信区间命令为nlparci，其调用格式为：

ci=nlparci（beta，r，J，α)

其中，输出参数beta，r，J是非线性拟合命令nlinfit输出的结果；输入ci是一个矩阵，每一行非别为每一个参数的（1-α)%的置信区间，默认值为0.05

（4）非线性回归交互命令nlintool，其典型调用格式为：

nlintool（x，y，fun，beta0)

其中，参数x，y，fun，beta0与命令nlinfit中的参数含义相同.

3　建立非线性拟合的函数模型

MATLAB的方法有很多种，本文选取居民消费水平为本次模型的因变量，全市财政收入为本次的自变量，选取二次函数拟合和指数函数拟合的方法对其进行非线性拟合.同时本次又选取了居民消费水平的数据为因变量，居民价格指数的数据为自变量，运用Logistic模型和双曲线函数拟合的方法对两个自变量和因变量进行非曲线拟合.

3.1二次函数拟合和指数函数拟合

选取居民消费水平数据为因变量，全市财政收入的数据为自变量.首先，应该明确居民消费水平和全市财政收入是何种关系，所以先绘制散点图.用MATLAB绘图命令绘制出的居民消费指数水平和全市财政收入的散点图如下图形：

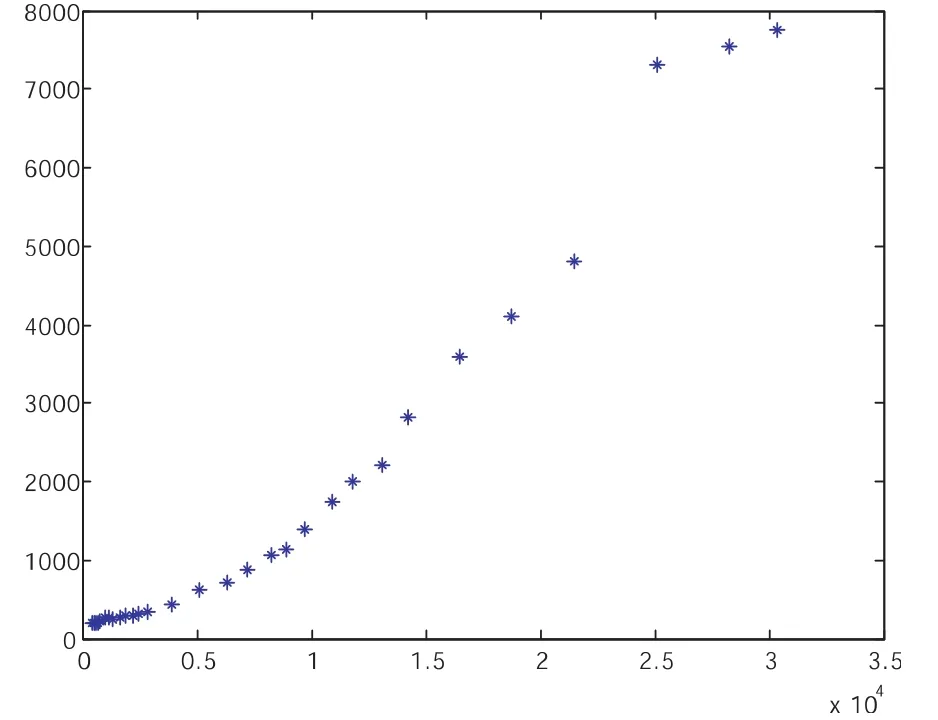
图1居民消费水平和全市财政收入散点图

从图中可以看出全市财政收入随着居民消费水平的提高而提高，即x和y不应该采用线性模型来描述，属于非线性.根据散点图的形状，考虑以下非线性模型：

指数函数：y=aebx

二次多项式回归模型：y=ax2+bx+c

用MATLAB软件进行曲线函数拟合得到指数函数方程为：y=0.0021e1.4737x

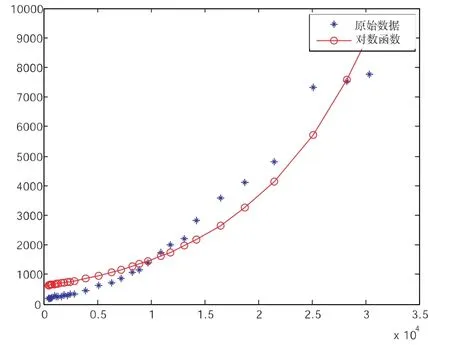
图2原始数据和对数函数拟合结果的散点图

图3居民消费水平和全市财政收入的交互图

图3中给出了居民消费水平和全市财政收入的非线性拟合交互图形，圆圈是本次实验的原始数据点，两条虚线（屏幕上显示为红色）为95%上、下置信区间的曲线，中间的实现是回归模型曲线（屏幕上显示为绿色）.

用MATLAB软件进行曲线函数拟合得到二次回归模型为：

y=0.0973x+64.2873

函数图象如下：

图4原始数据和二次函数拟合的散点图

相比较之下，二次函数的拟合程度比指数函数的拟合程度好

3.2 Logstic模型拟合和双曲线拟合

选取居民消费水平的数据为本次模型拟合的因变量，居民价格指数的数据为自变量，运用MATLAB绘图命令绘制出居民消费水平和居民消费价格指数的散点图像为下图：

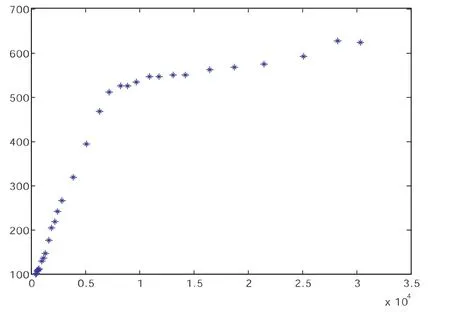
图5居民消费水平和居民消费价格指数的散点图

图5可以看出，居民消费水平和居民消费价格指数的变化呈非线性过程，而且存在一个与横左边平行的渐近线，可以用Logistic曲线模型和双曲线模型进行拟合

用MATLAB软件进行曲线函数拟合，运行结果为：beta=0.0028 0.2916

用MATLAB软件进行曲线函数拟合，运行结果为：beta=0.0014 5.8365 R2=0.9843

由运行结果可决系数为0.9843，表明拟合程度较好.

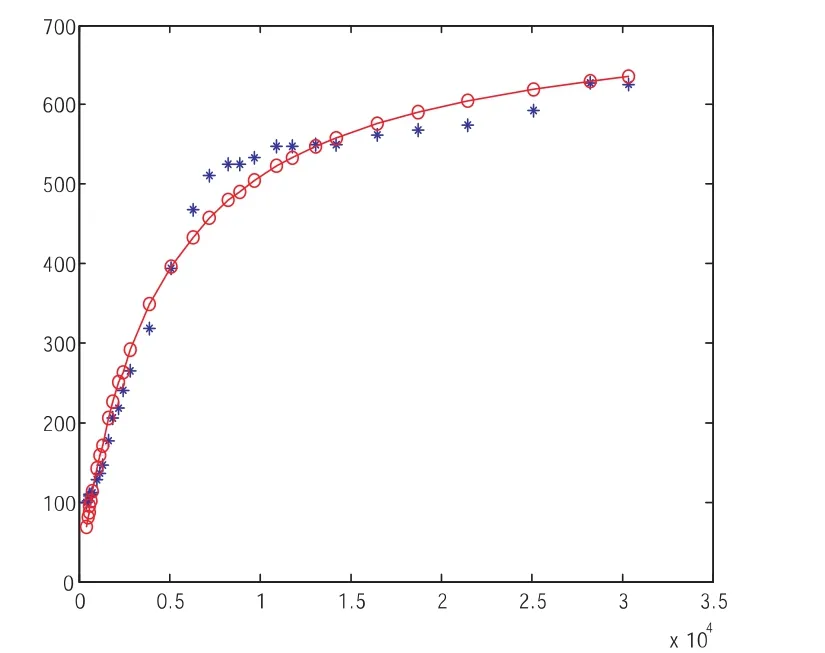
图6原始数据和双曲线函数拟合的散点图

图7居民消费水平和居民消费价格指数的交互图

图7给出了居民消费水平和居民消费价格指数的非线性拟合交互图形，图中的圆圈是本次实验的原始数据点，两条虚线（屏幕上显示为红色）为95%上、下置信区间的曲线，中间的实现是回归模型曲线（屏幕上显示为绿色）.

——————————

参考文献：

〔1〕占永革，黄湘燕，龚剑.化学分析中非线性曲线拟合结果的不确定度的评定[J].冶金分析，2011，31(8)：26-30.

〔2〕陈旭红.用Origin软件的线性拟合和非线性曲线拟合功能处理实验数据[J].江苏技术师范学院学报，2006，12(6)：85-89.

〔3〕金明，张莲花，等．MATLAB工具箱应用[M]．北京：电子工业出版社，2004.

〔4〕Gerald Reektenwald．数值方法和MATLAB实现与应用[M]．北京：机械工业出版社，2004.

〔5〕赵静，但琦.数学建模与数学实验（第二版）[M].北京：高等教育出版社，2004.

〔6〕李庆扬，王能超，等．数值分析[M]．北京：清华大学出版社，2001.

〔7〕李柏年，吴礼斌.MATLAB数据分析方法[M].北京：机械出版社，2012.

〔8〕敖斌，王国体．基于MATLAB建筑物沉降的灰色预测[J]．地基与基础，2008，22(6)：818-820.

〔9〕唐家德.基于MATLAB的非线性曲线拟合[J].计算机与现代化，2008(06)：15-19.

〔10〕陈岚峰，杨静瑜，崔崧，潘庆超，李柳.基于MATLAB的最小二乘曲线拟合仿真研究[J].沈阳师范大学学报，2014.32(1)：75-79.

〔11〕韩寄德，王祖顺，王春青.非线性曲线TLS法拟合[J].测绘与空间地理信息，2015(3)：170-172.

〔12〕李玉星，王振荣，鲁旭东，王攀峰.对ISAR成像中扫频非线性的曲线拟合[J].北京航空航天大学学报，2001，27 (2)：150-154.

〔13〕严晓明，郑之.BP与RBF网络在一些非线性曲线拟合上性能的比较[J].福建农林大学学报（自然科学版），2011，40(6)：653-656.

〔14〕应六英.实现非线性曲线拟合的LINGO方法应用实例[J].江西电力职业技术学院学报，2014，27(4)：51-56.

中图分类号：TP311；O241

文献标识码：A

文章编号：1673-260X（2015）07-0003-03