地震作用下密频拱桥Rayleigh阻尼的优化解

雷素素，高永涛，潘旦光

（北京科技大学土木与环境工程学院，100083北京）

地震作用下密频拱桥Rayleigh阻尼的优化解

雷素素，高永涛，潘旦光

（北京科技大学土木与环境工程学院，100083北京）

为建立频谱密集结构的阻尼矩阵，以地震反应谱理论为基础，基于完全二次组合（CQC）提出了求解Rayleigh阻尼系数的优化分析方法.在此基础上，为实现任意阶模态阻尼比等于精确阻尼的要求，利用Lagrange乘子法进一步建立了求解Rayleigh阻尼系数约束优化方法.以一座斜交曲梁下承式钢结构吊索拱桥为例，讨论优化分析所得Rayleigh阻尼系数的稳定性，比较了不同的优化目标组合、约束条件对优化参考频率和地震反应的影响，以及约束优化解中约束模态的选取问题.数值分析结果表明，与平方和开平方组合（SRSS）相比，CQC组合所得的Rayleigh阻尼系数的地震反应计算误差更小，约束模态应该选取对结构地震反应有显著贡献的第一阶模态.

密频结构；地震反应；Rayleigh阻尼；优化分析；完全二次型组合

桥梁作为生命线工程之一，其抗震安全性历来备受瞩目.为满足交通功能和城市景观功能，世界各地因地制宜的修建大量造型优美的非规则桥梁.对于非规则桥梁，其动力响应特性复杂，因此，中国规范［1］要求采用时程分析法、多振型反应谱法和功率谱法等分析方法来确保其抗震性能.当采用直接积分法进行时程反应分析时，必然涉及阻尼矩阵的建立问题.在各种阻尼矩阵的构建方法中，Rayleigh阻尼［2－3］由于数学处理的便利性而广泛应用到各种桥梁的地震反应分析中，通常Rayleigh阻尼系数通过指定两阶参考频率进行计算.文献［4－5］以最低两阶横向模态为参考模态形成连续梁桥的Rayleigh阻尼；文献［6］以基频和对结构有重要影响模态为参考模态构造Rayleigh阻尼，对大跨双曲拱桥进行地震分析；文献［7］建议选择两个振型参与系数大的振型来确定Rayleigh阻尼矩阵，对于大型复杂结构，直接指定两阶合理的参考频率有一定的难度，此时可采用优化理论的方法计算Rayleigh阻尼系数；文献［8］提出采用最小二乘法计算α和β，最小二乘法没有考虑各阶模态对动力反应贡献的差异，不是一种合理计算方法［9］；文献［10］建立了基于多参考振型的加权最小二乘法计算Rayleigh阻尼；文献［11－12］基于振型叠加反应谱理论和平方和开平方原理（SRSS），建立了Rayleigh阻尼系数的优化解；文献［13－14］分别通过显式方法和拉格朗日乘子法求解了有约束模态的Rayleigh阻尼系数，但是并未考虑约束模态的影响和约束模态的选取方法.

由反应谱的理论可知，SRSS组合没有考虑模态之间的相互影响，比较适合频率较为稀疏结构的反应分析.对于频率密集的结构，频率比在0.85以内的模态之间相互影响很大［15］.为此，在文献［11，14］基础上，本文主要进行两方面研究：基于完全二次组合（CQC）推导了优化Rayleigh阻尼系数的计算公式，以模态相关系数考虑模态之间的相互影响，并与SRSS组合优化方法进行比较，讨论密频结构目标函数的建立问题；采用Lagrange乘子法建立基于CQC组合的Rayleigh阻尼系数约束优化求解方法，在此基础上，以张家口一座斜交曲梁下承式钢结构吊索拱桥为例，讨论约束模态的选取方法及约束条件对优化结果的影响.

1 Rayleigh阻尼系数约束优化解

在地震输入作用下，多自由度体系的强迫振动方程可表示为

式中：u、ù和ü分别为相对位移、相对速度和相对加速度向量，I为地面运动影响向量，üg（t）为地面运动加速度，M、C和K分别为质量矩阵、阻尼矩阵和刚度矩阵.假设C为Rayleigh阻尼，即

式中：α和β分别为质量比例阻尼系数和刚度比例阻尼系数.若已知结构前N阶的频率ωn和模态φn（n＝1，2，…，N），则由式（2）所得第n阶模态的近似阻尼比为

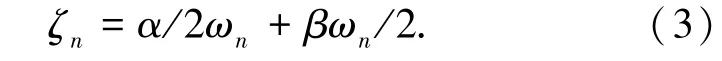
若第n阶模态的精确阻尼比为ζ∗n，由模态叠加反应谱法的理论可知，第n阶模态对第k自由度的最大位移反应ukn由Rayleigh阻尼所得的近似解和精确解可分别表示为：

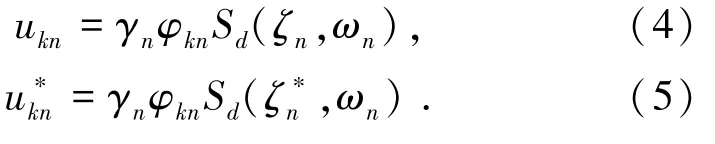
式中上标∗表示精确解.γn＝－φn T MI／Mn，Mn＝φn T Mφn分别为第n阶振型参与系数和振型质量，Sd（ζn，ωn）为第n阶模态的位移反应谱，其计算式为

为考虑频率密集结构模态之间的相互影响，基于反应谱理论中的相关系数和CQC组合，以第k自由度位移反应建立目标函数：

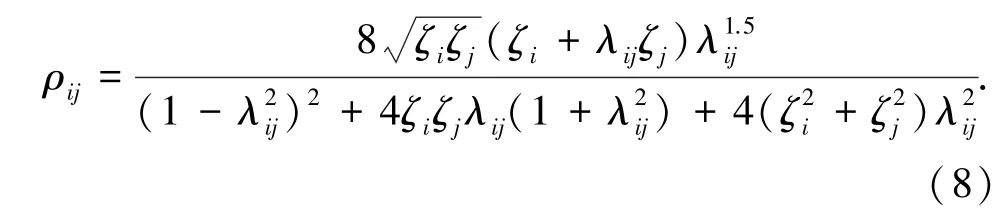
式中λij＝ωi／ωj，ρij为第i阶模态和第j阶模态的相关系数［3］.显然，式（7）是α和β的隐函数.为简化计算，将位移反应谱函数采用一阶Taylor级数展开：

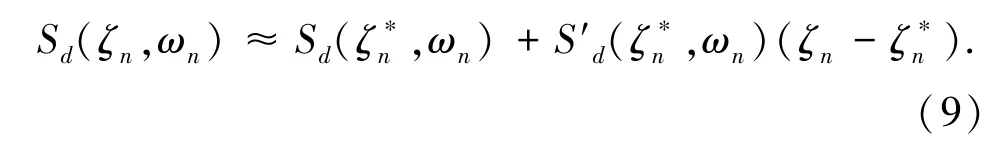
式中S′d（ζ∗n，ωn）＝∂Sd（ζ∗n，ωn）／∂ζn.将式（9）代入式（8），整理后可得

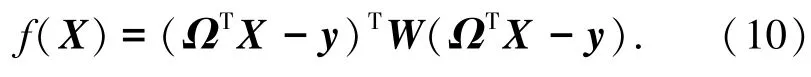
式中：

为得式（10）的最小值，令

化简后可得

式中 G＝ΩWΩT，R＝ΩWy.求解式（12）即可得Rayleigh阻尼系数的无约束优化解.如果式（10）的权重矩阵仅保留主对角线元素，而令其余元素为零，即可得到基于SRSS组合的优化Rayleigh阻尼系数，由此可知，基于CQC组合的优化方法计算工作量增加很小.为使第r阶模态的阻尼比等于精确值ζ∗r，则可增加约束条件：

采用Lagrange乘子法，式（13）约束条件下，式（10）的目标函数可表示为

将式（14）分别对X与λ求导，并令相应的导数为零可得代数方程组：

求解式（15）方程，所得的Rayleigh阻尼系数为第r阶模态阻尼比等于精确解的约束优化解.

2 工程概况及输入地震波

为验证以上算法合理性和精度以及约束条件必要性，以张家口通泰大桥为例，探讨不同方法所得Rayleigh阻尼系数对桥梁地震反应的影响.通泰大桥是一座斜交曲梁下承式钢结构吊索拱桥（图1），桥的拱圈斜跨主梁，水平投影与主梁跨中轴线切向夹角19.5°，主梁与拱圈之间由28根吊索相连，主桥为跨径190 m的钢箱梁弯桥，弯曲半径600 m，拱圈最大矢高62.118 m，拱脚间距180 m，主梁和拱圈的截面尺寸见图1.

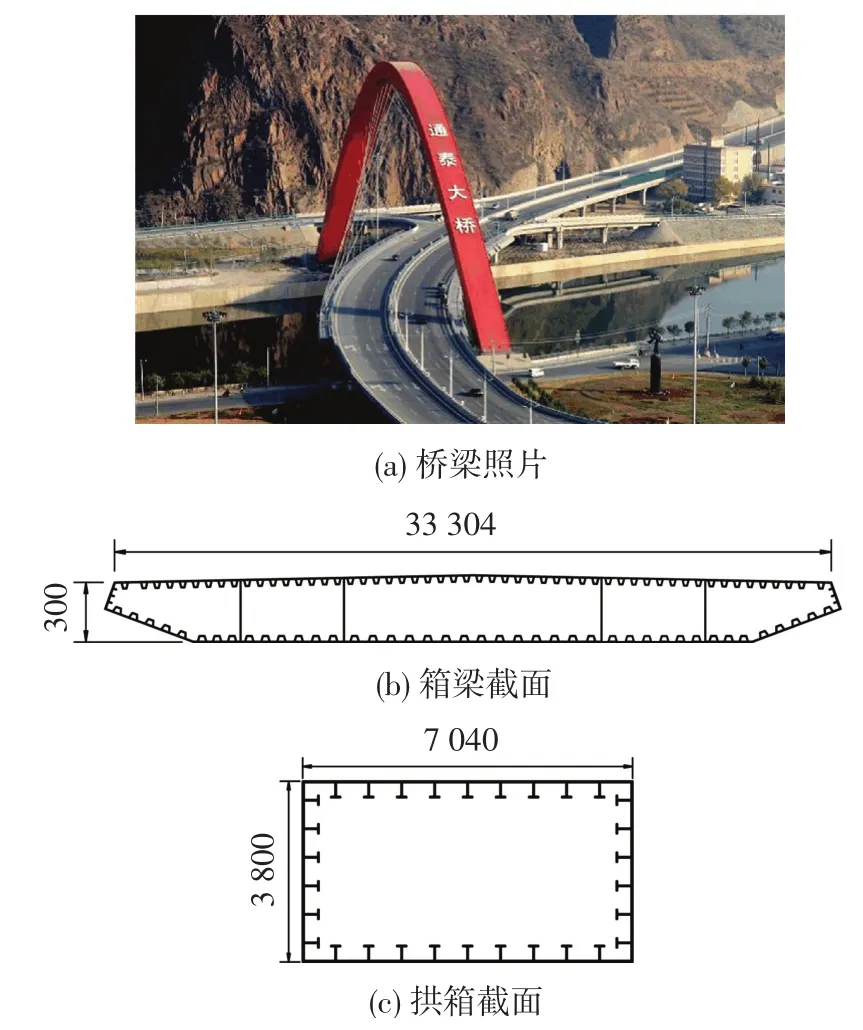
图1 桥梁示意（mm）

桥梁采用单脊梁式建立有限元模型，见图2.模型中以Timoshenko梁单元（beam189）剖分主梁和拱，以索单元（link180）剖分吊索.钢的弹性模量为2.06×1011Pa，密度7 850 kg／m3，泊松比0.3.桥面铺装及栏杆采用附加质量的方式考虑，每个梁单元节点附加质量为1.23×104kg.根据设计图纸，拱脚为固定支座，梁端为铰支座.模型共包括431个单元，676个节点，其中坐标系：x方向为横桥向，y方向为顺桥向，z方向为竖向.并设各阶模态的精确阻尼比为0.02.建立有限元模型后，在恒载作用下，索力调整以桥面1／8点竖向位移的平方和最小为优化目标，以跨中位移小于l0／400（l0为主梁跨径）为约束条件进行优化计算，所得索力和桥梁应力作为后续地震反应分析的初始应力状态.

在式（9）计算中，权重系数wij涉及第k自由度的模态位移φkn，即优化的参考自由度问题.根据文献［11］的研究成果，以拱顶这一最大位移反应的自由度为参考自由度.

在输入地震波方面，选择3条不同类型的地震波作为桥梁的地震输入，并将地震波峰值加速度统一调整为0.1 g.地震波的加速度时程和7个阻尼比（ζ＝0.005、0.01、0.02、0.03、0.05、0.10、0.20）下的位移反应谱见图3.

图2 桥梁有限元模型

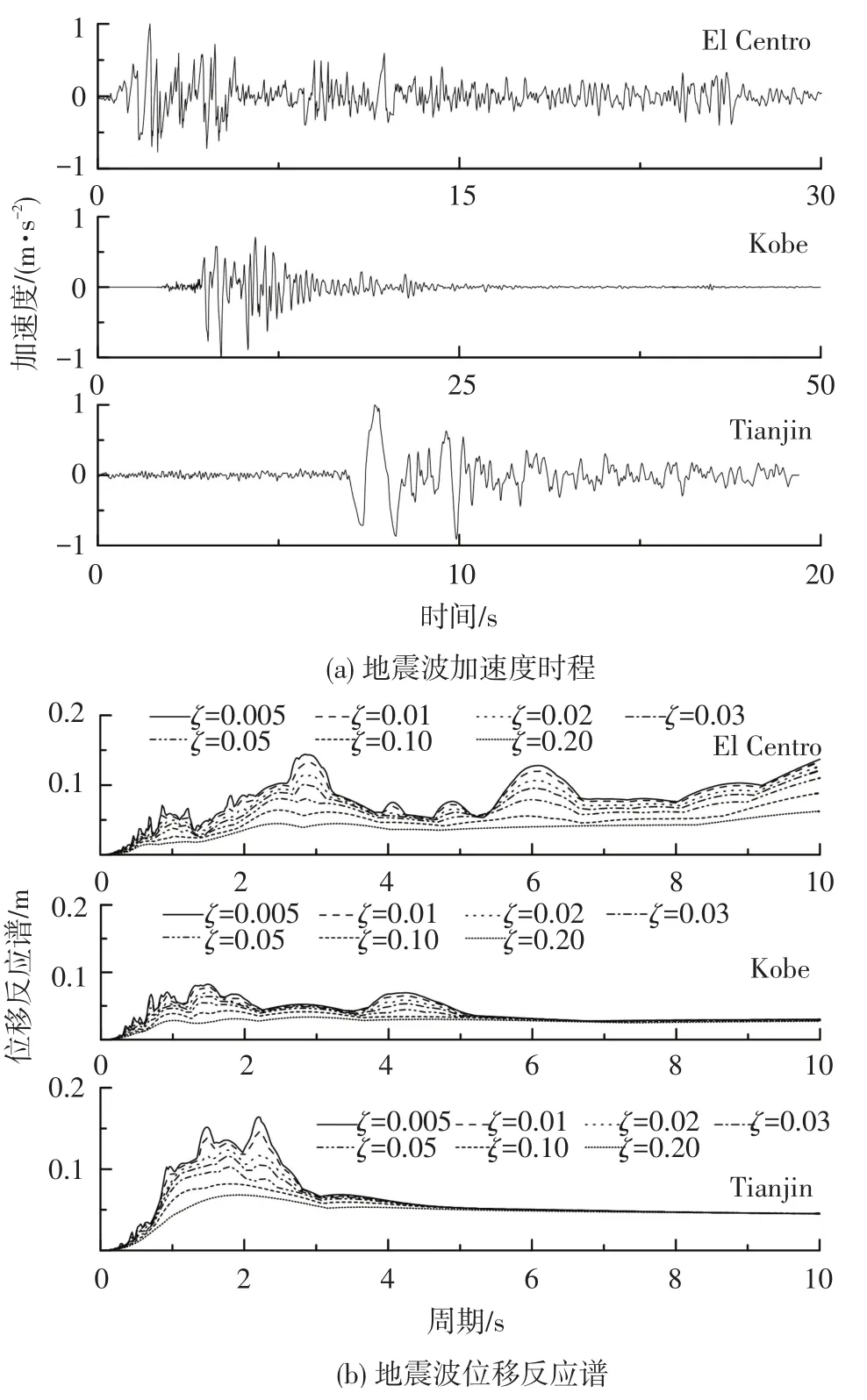
图3 地震波加速度时程及其位移反应谱

对于实际地震输入下的反应谱必然是极不规则的曲线，因此，无法建立位移反应谱显式表达式.此时可由7个阻尼比的反应谱通过曲线拟合并求导计算得到［14］，即

3 计算结果及分析

3.1 桥梁自振特性

对于吊索拱桥，拉索的应力对结构的动力特性有显著影响.为考虑重力对拉索应力的影响及拉索的几何刚度，拱桥的模态分析分两个步骤：计算重力及初始应力下结构的应力；进行有预应力的模态分析.结构主要阶数的自振频率、振型参与质量、累积振型参与质量和振型特征见表1.可见当模态阶数达198阶时，x和y方向的累积振型参与质量都超过90%.

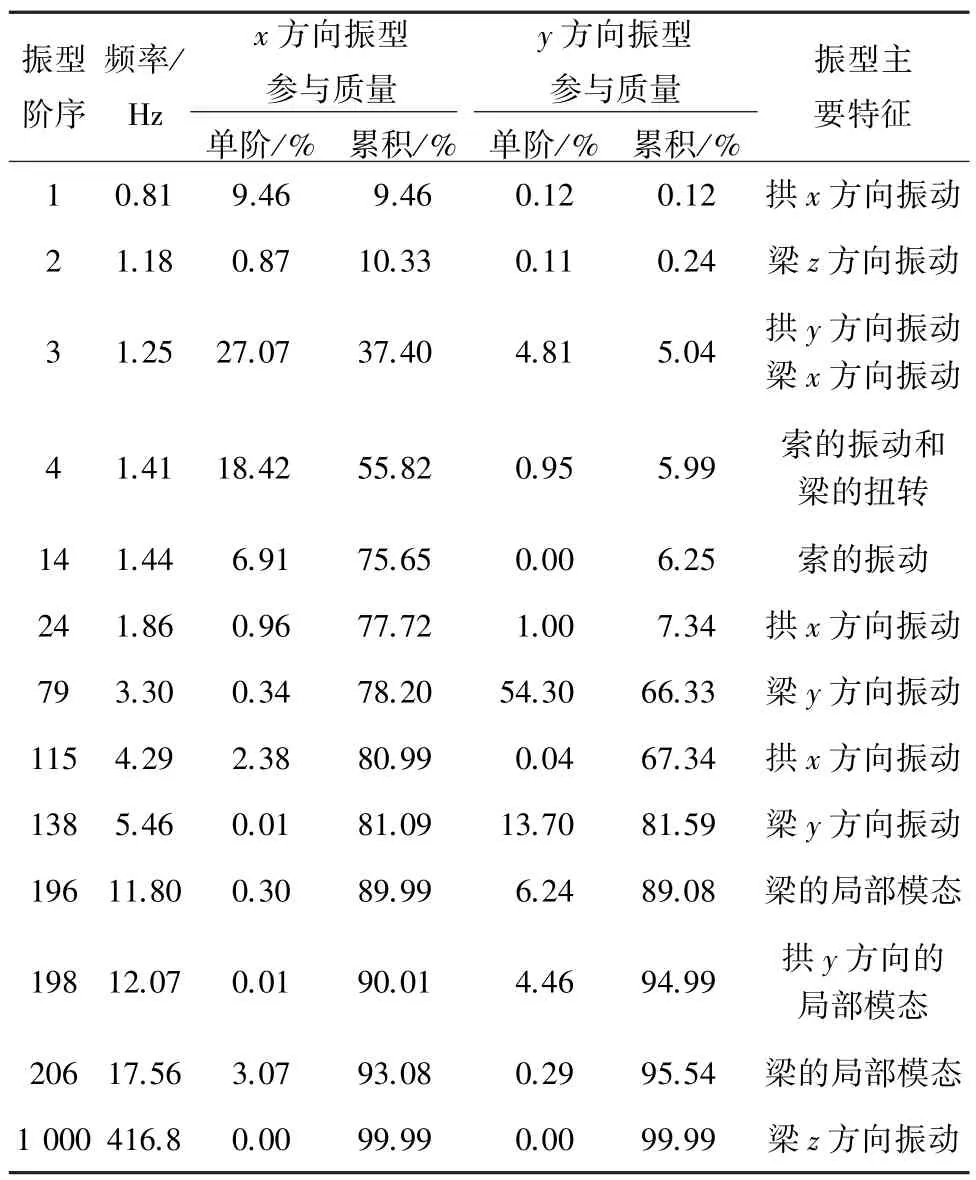
表1 部分显著贡献模态

从模态分析结果看，第1阶模态是拱横桥向（x方向）振动的第1个显著贡献模态，第3阶模态是拱顺桥向（y方向）振动的第1个显著贡献模态，且是横桥向振型参与质量最大的一阶模态；因此，建立式（12）的约束条件时，横桥向的约束模态取为第1阶，同时，也计算第3阶模态为约束模态作为对比.在顺桥向约束模态的选取方面，分别选择结构的基频（第1阶）和对y方向振动有显著贡献的第1个模态（第3阶）作为约束模态，进行对比分析，以理解基频的含义.两种做法虽然最终选取的约束模态都是第1阶和第3阶，但对比分析的目的并不相同.

3.2 参与优化计算模态个数影响

由式（6）可知，Rayleigh阻尼系数优化计算与参与优化计算的模态个数N有关.图4、5为x方向激励下不同方法所得Rayleigh阻尼系数随模态数N的变化情况，y方向激励下的计算结果具有相同的变化规律.图中SRSS和CQC为无约束优化分析的结果，SRSS1、SRSS3、CQC1和CQC3表示约束优化解.字母后面的数字表示约束模态的阶数，譬如，CQC3表示第3阶模态的阻尼比等于精确值作为约束条件，用CQC组合作为模态函数所得的约束优化解.从Rayleigh阻尼系数曲线看，当累积振型参与质量超过90%的模态参与优化计算，无论是SRSS组合还是 CQC组合，无论是无约束还是有约束，Rayleigh阻尼系数的计算结果趋向于一个稳定值.因此，下面计算分析时，都以 N＝198所得的优化Rayleigh阻尼系数进行时程分析.

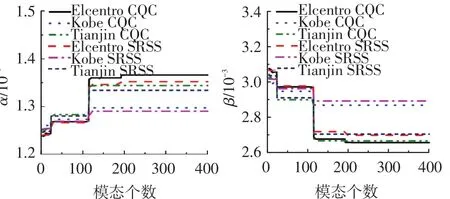
图4 x方向激励无约束优化解

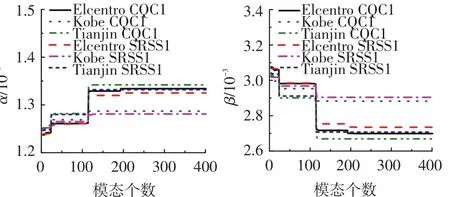
图5 x方向激励约束优化解

不同优化算法计算所得的α和β列于表2、3.将α和β代入式（3）计算各阶模态阻尼比，并称优化计算所得阻尼比等于精确阻尼比的频率为优化参考频率，不同方法所得优化参考频率也列于表2、3.

由计算结果可知：1）对比CQC和SRSS所得Rayleigh阻尼系数可知，CQC组合所得α更大而β更小，由此导致CQC组合所得的第二个优化参考频率大于SRSS，但第一个参考频率基本相同，这表明CQC组合更多地考虑了高阶模态的影响；2）对比无约束和有约束优化解的计算结果可知，当约束模态是相应激励方向第一个显著贡献模态（x方向激励时选第1阶，y方向激励时选第3阶），约束优化解的第2个参考频率与无约束优化解的基本相同，且无约束优化解的第一个参考频率也接近约束模态，对于这种情况，增加约束条件对优化计算影响很小；3）不同地震波输入下，优化参考频率并不相同，这是由于不同地震波的频谱特性并不相同，而本文优化分析方法可综合考虑结构动力特性和输入地震波的频谱特性的影响.

表2 x方向激励下优化Rayleigh阻尼系数及参考频率

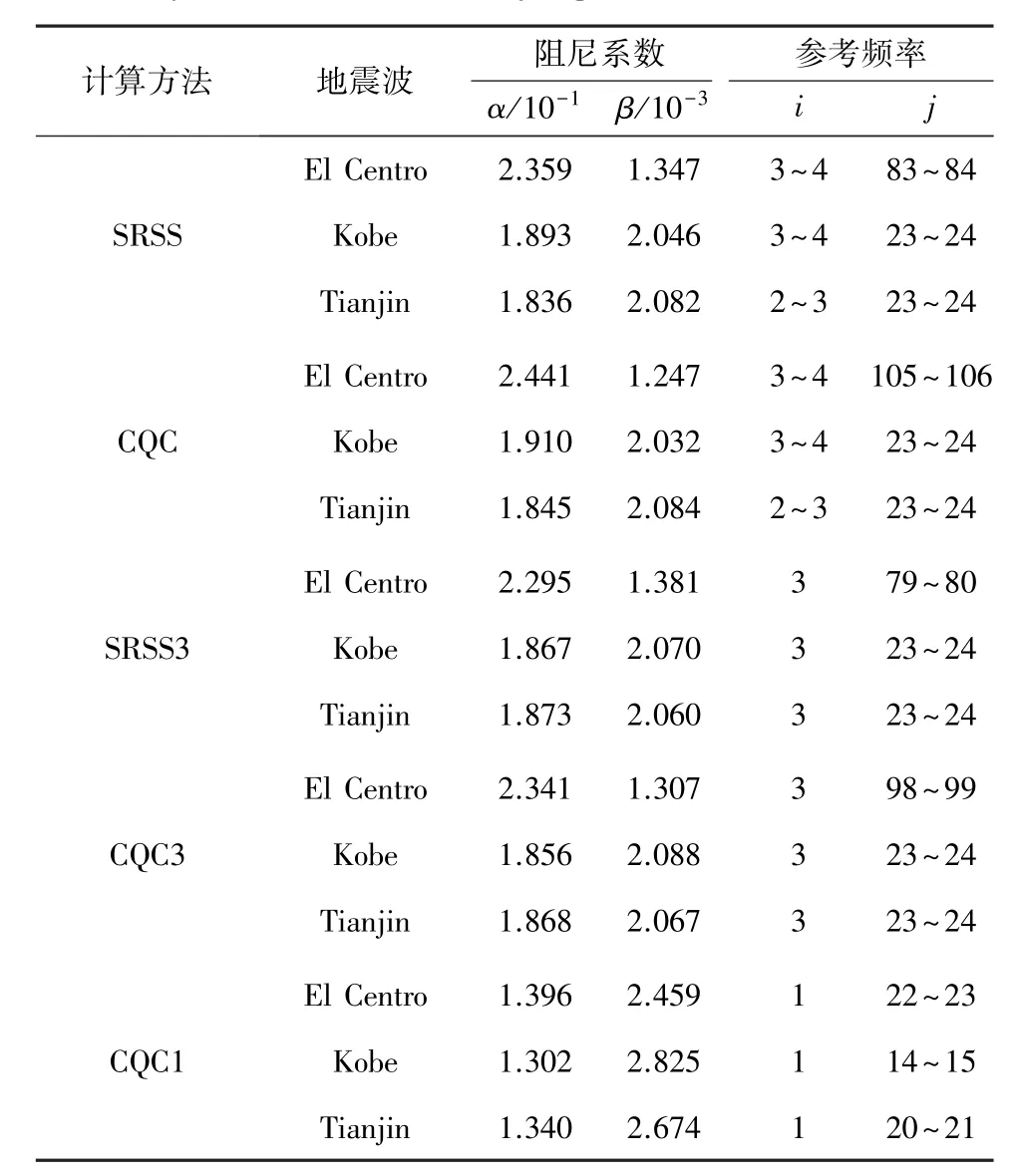
表3 y方向激励下优化Rayleigh阻尼系数及参考频率

3.3 反应峰值的计算误差

由模态分析可知，当模态个数达1 000阶时，体系x方向和y方向的累积振型参与质量都超过99%.为此，采用各阶模态的精确阻尼比，以1 000阶模态的振型分解法计算所得的结构动力反应量作为精确解，并记为r∗.采用Rayleigh阻尼模型所得的近似解记为r，则Rayleigh阻尼模型计算结果的相对误差e为

作为对比的传统Rayleigh阻尼计算方法，在x方向激励时，选用i＝1，j＝115和i＝1，j＝198两模态组合方式，在y方向激励时，选用i＝1，j＝138和i＝3，j＝138两种模态组合方式计算相应的Rayleigh阻尼矩阵.下面分别从拱顶位移峰值，拱脚的轴力、剪力的峰值比较不同方法所得Rayleigh阻尼对计算精度的影响.

在不同地震波沿x方向激励作用下，不同方法所得Rayleigh阻尼的计算误差见表4.可看出：1）从总体统计角度看，使用优化方法得到的计算误差都小于传统方法，而不考虑输入地震波影响的传统计算方法，不同地震波的计算误差差别很大；2）除CQC3外，无约束优化解和约束优化解的计算误差基本相同，这表明无约束优化方法具有自动识别显著贡献模态的能力，而无需人为指定约束条件进行约束优化分析；3）采用SRSS组合进行优化分析结果具有很好精度，而CQC组合的计算精度更高，这是由于SRSS组合的优化方法所得的Rayleigh阻尼系数使反应谱组合中自相关项的计算误差最小，这同时也降低了互相关部分的计算误差，而CQC组合考虑自相关和互相关项误差的影响，因此，可在一定程度上提高计算精度.其最明显的影响是对拱脚剪力计算精度的提高，这是由于拱脚剪力中包含高频成分，CQC组合的第2个优化参考频率高于SRSS组合，因此，相应地提高剪力的计算精度；4）CQC3方法的计算结果是优化分析中最差的，这表明任意选择一阶显著贡献模态作为约束模态是不合理的.

表5为y方向激励作用下的计算误差.由计算结果可以看出：1）从总体统计角度看，使用优化方法得到的计算误差也小于传统方法，而且变化规律和x方向激励下的基本一致，这再次表明优化分析的有效性；2）由于y方向激励下，第一个显著贡献模态是第3阶，因此，以第3阶作为约束模态的计算精度显著高于以第1阶作为约束模态，这表明，所谓的动力反应基频应该是指对结构有显著贡献的第1阶模态.

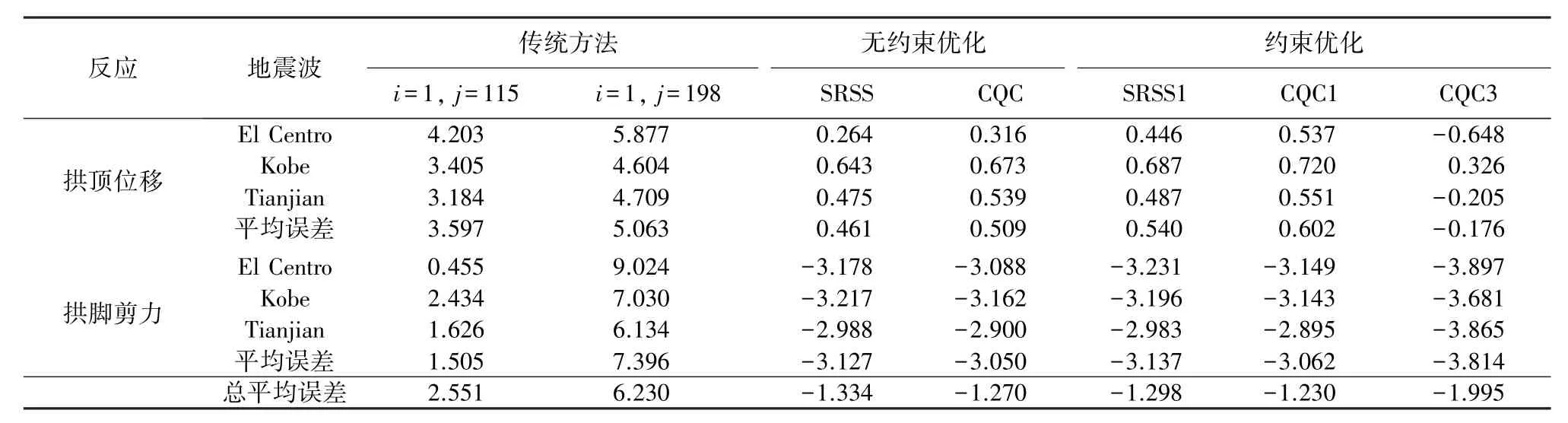
表4 x方向激励下的计算误差

表5 y方向激励下的计算误差

4 结 论

1）优化Rayleigh阻尼系数与参与计算的模态数目有关，计算中应使优化方程包含所有的显著贡献模态.实际计算时，可选取累计振型参与质量超过90%的模态数进行计算.

2）优化分析方法所得Rayleigh阻尼系数是综合考虑结构动力特性和地震波频谱特性影响的结果，无需人为确定两阶参考频率，便于工程应用，且从统计角度看，计算误差小于传统误差.

3）与SRSS组合相比，CQC组合的优化方法在计算工作量增加不多的情况下，所得的优化Rayleigh阻尼系数可提高结构地震反应精度.

4）采用约束优化分析时，应该选用与激励方向相对应的第1个显著贡献模态作为约束模态，此时所得的Rayleigh阻尼系数具有很高的计算精度.简单选择第1模态或任意选择1阶模态作为约束模态的做法应该避免.

［1］JTG／T B02－01—2008公路桥梁抗震设计细则［S］.北京：人民交通出版社，2008.

［2］R克拉夫，J彭津，著.结构动力学［M］.第2版.王光远，译.北京：高等教育出版社，2006.

［3］CHOPRA A K.Dynamics of structures： theory and applications to earthquake engineering［M］.New Jersey：Englewood Cliffs，Prentice-Hall，1995.

［4］CHIARA C，RUI P.Seismic response of continuous span bridges through fiber-based finite element analysis［J］.Earthquake Engineering and Engineering Vibration，2006，5（1）：119－131.

［5］KHAN E，SULLIVAN T J，KOWALSKY M J.Direct displacement-based seismic design of reinforced concrete arch bridges［J］.Journal of Bridge Engineering，2013，19（1）：44－58.

［6］ZHANG Yun，HUANG Xiufeng，LIBei.Seismic analysis of long span double-curved arch bridge［J］.Advanced Materials Research，2012，594：1532－1536.

［7］楼梦麟，张静.大跨度拱桥地震反应分析中阻尼模型的讨论［J］.振动与冲击，2009，28（5）：22－26.

［8］刘红石.Rayleigh阻尼比例系数的确定［J］.噪声与振动控制，1999，（6）：21－22.

［9］潘旦光，高莉莉，李小翠.求解Rayleigh阻尼系数的加权最小二乘法［J］.计算力学学报，2015，32（1）：70－76.

［10］YANG Dabin，ZHANG Yigang，WU Jinzhi.Computation of Rayleigh damping coefficients in seismic time-history analysis of spatial structures［J］.Journal of the International Association for Shell and Spatial Structures，2010，51（2）：125－135.

［11］潘旦光.地震反应分析中Rayleigh阻尼系数的优化解［J］.工程力学，2013，30（11）：15－20.

［12］PAN Danguang，CHEN Genda，WANG Zuocai.Suboptimal Rayleigh damping coefficients in seismic analysis of viscously-damped structures［J］.Earthquake Engineering and Engineering Vibration，2014，13（4）：653－670.

［13］董云，楼梦麟.基于结构基频确定Rayleigh阻尼系数的优化方法及其讨论［J］.湖南大学学报（自然科学版），2014，41（2）：8－13.

［14］潘旦光，靳国豪，高莉莉.大跨斜拉桥Rayleigh阻尼系数的约束优化解［J］.振动与冲击，2014，33（16）：34－41.

［15］GB 50011—2010建筑抗震设计规范［S］.北京：中国建筑工业出版社，2010.

（编辑赵丽莹）

An optim ization solution of Rayleigh dam ping coefficients on arch bridges w ith closely-spaced natural frequencies subjected to seism ic excitations

LEISusu，GAO Yongtao，PAN Danguang

（School of Civil and Environmental Engineering，University of Science and Technology Beijing，100083 Beijing，China）

An optimization solution of Rayleigh damping coefficients is proposed to construct the dampingmatrix of structureswith closely-spaced natural frequencies based on the seismic response spectrum theory and the complete quadratic combination（CQC）rule.A constrained optimization method is further developed to enforce the arbitrary ordermode damping ratio equal to the precise value by Lagrangemultipliermethod.A curved girder skew through steel suspension arch bridge is analyzed to investigate the characteristics of the proposed method.Firstly，the solution stability of optimal Rayleigh damping coefficients is discussed，Secondly.the effects of the different combinations of optimal objective functions and constraint conditions on optimal reference frequencies and seismic response are compared，and the selection of constraintsmode in constrained condition is also discussed.Numerical results show that the seismic response calculation error is smaller while the Rayleigh damping coefficients is obtained from CQC rather than the square rootof sum square（SRSS）combination.The constrained mode should be specified as the first order significantmode corresponding to structural seismic responses.

closely spaced natural frequencies structure；seismic response；Rayleigh damping；optimization analysis；complete quadratic combination

TU311.3；U442.5＋5

A

0367－6234（2015）12－0123－06

10.11918／j.issn.0367-6234.2015.12.022

2015－04－09.

国家自然科学基金（51078032）；北京市自然科学基金（8143037）.

雷素素（1988—），女，博士研究生；高永涛（1962—），男，教授，博士生导师；潘旦光（1974—），男，研究员，博士生导师.

潘旦光，pdg＠ustb.edu.cn.