非均匀温度场Fe－0.06%C合金焊接接头凝固过程模拟分析

张 敏，汪 强，徐蔼彦，邢 奎

（西安理工大学材料科学与工程学院，西安710048）

非均匀温度场Fe－0.06%C合金焊接接头凝固过程模拟分析

张 敏，汪 强，徐蔼彦，邢 奎

（西安理工大学材料科学与工程学院，西安710048）

摘 要：利用元胞自动机和有限差分（CA－FD）法，采用宏－微观两种尺度，将宏观温度场与微观枝晶生长过程耦合在一起，再现了Fe－0.06%C二元合金焊接熔池的凝固过程.同时，探讨了边界散热速率对焊接熔池中枝晶生长形貌及晶粒尺寸的影响；分析了形核基底数与枝晶生长间的关系；并用实验对模拟结果进行了验证.结果表明，在熔池凝固过程中，温度梯度沿散热边界向绝热边界方向不断减小，等温线弧度不断增大；熔池散热边界附近的液相中溶质浓度远远高于绝热边附近和模拟区域中心的液相溶质浓度；模拟区域内的温度梯度随着边界散热速率的增大而升高.此外，随着形核基底的增加，柱状晶数量基本不变；而等轴晶数量不断增多，分布范围逐渐扩大，但尺寸有所减小.模拟结果反映了焊接熔池的凝固过程，并与实验结果吻合，为实际焊接工艺的选取提供了一定的参考.

关键词：焊接冶金；数值模拟；焊接熔池；宏－微观模型；微观组织；枝晶生长

钢铁材料是现代工业发展中使用最广泛的结构材料之一.钢结构的连接通常采用焊接的方法来实现，由此钢铁的焊接性能受到各界专家学者的重视.焊接接头的性能主要取决于接头处的微观组织，而焊接接头的微观组织与焊接熔池的凝固过程紧密相关.在材料给定的条件下，可以调整焊接工艺来获取高强度、高韧性的焊接接头.焊接工艺调整的实质是对焊接熔池的凝固过程进行控制，以期获得性能优良的微观组织；然而，通过实验的方法来研究焊接凝固微观组织，不仅耗时、耗力还耗资，而且得出的规律具有很大的局限性［1］.近几十年，随着计算机技术的不断发展，通过模拟研究合金凝固的微观组织技术得到了突飞猛进的发展［2－7］.在此期间出现了多种模拟方法，其中CA法以其能够随机叠加多种物理现象和随机分布函数的空间位置受到材料领域专家和学者的广泛关注［8］.

CA法兴起于20世纪50年代，主要运用于生物领域［9］.直到20世纪80年代，Rappaz和Gandin等人［10］首次利用CA法模拟计算金属凝固枝晶的生长过程.随后，Lee P.D.和Wang W.［11］建立了CA－FD二元合金耦合模型，该模型研究了枝晶偏轴正方形生长和界面上所有点的生长速度对枝晶各向异性生长的影响.在国内，许林，郭洪明［12］采用元胞自动机法建立了铝合金结晶过程中枝晶结构转变和微观组织形成的三维CA模型，模拟得到了Al－15%Cu合金结晶过程中单个枝晶生长和多晶粒生长结果.朱鸣芳［13］对已有的元胞自动机模型加以改进，模拟了在等温过冷熔体中单个晶粒的自由生长，沿着过冷度方向定向凝固时柱状树枝晶的竞争生长及等轴树枝晶的变化过程.然而这些针对微观组织的模拟研究主要集中于传统的铸造领域.近几年，CA法在模拟焊接过程的微观组织变化中虽也取得了一定的进展［14－15］，但相对滞后.因此，基于元胞自动机法的焊接过程微观组织模拟亟待进一步探索研究.

本文建立了宏－微观耦合的CA－FD模型，并根据现有的枝晶生长理论，在MATLAB平台上自主编程，模拟了Fe－0.06%C二元合金焊接凝固过程中的非均匀温度场、溶质浓度分布和枝晶形貌，分析了模型中关键参数变化对枝晶演变过程的影响，并用实验对模拟结果进行了验证.

1　熔池凝固模拟模型和算法描述

焊接接头通常有对接、角接、T型和搭接4种形式，文中针对对接接头建立熔池凝固过程的模拟模型，模拟区域如图1（a）所示.

1.1 焊接熔池温度场控制模型

温度场的有效控制是模拟焊接熔池凝固过程的前提.熔池凝固过程的温度变化符合热扩散的普遍规律，其热的传递包括传导、对流和辐射，而在熔池底部处以热传导为主，对流和辐射传热引起的温度变化十分微弱.故在模拟焊接熔池底部附近的温度场时，可建立一个简化的二维传热模型.简化后的模型忽略对流和辐射两种传热形式.

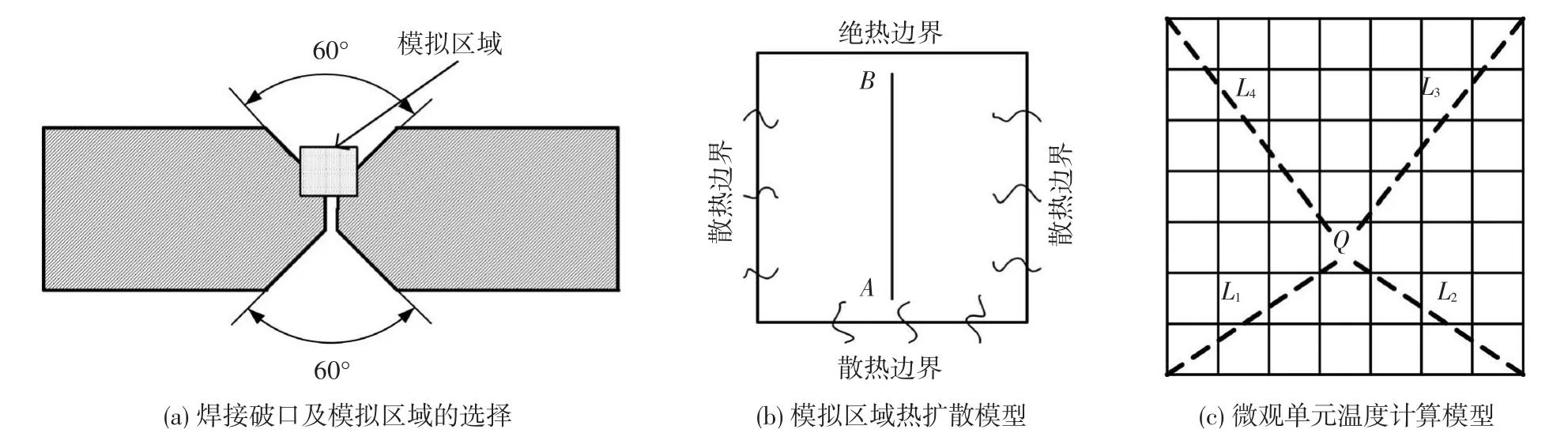
图1　模拟区域的选择和温度控制模型

在宏观温度场模拟过程中，假定熔池的一边绝热，其余三边以恒定的导热速率向熔池外散热，如图1（b）所示.故本文采用下式计算宏观边界单元的温度：

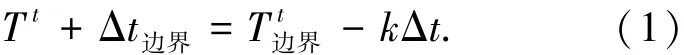
模拟区域内部的宏观单元温度控制方程为

式中：T为温度，t为时间，fS为固相份数，α为导热系数，L为凝固潜热，CP为比热容.数值计算过程中，采用有限差分法来获得熔池内部节点的宏观温度.

在微观组织模拟中，微观单元的尺度通常为微米级.获得宏观单元温度后，利用插值公式获取微观单元的温度，如图1（c）所示.插值公式为

式中：TQ为微观单元温度，Ti为与当前单元相邻的宏观单元温度，Li为微观单元Q到宏观温度单元顶点的距离.

1.2 形核与生长模型

实际金属凝固过程中，晶粒总是连续不断的形成并长大.因此本文采用Rappaz［10］等人提出的准连续形核模型.在过冷度已知的情况下，晶核密度满足正态分布规律，即

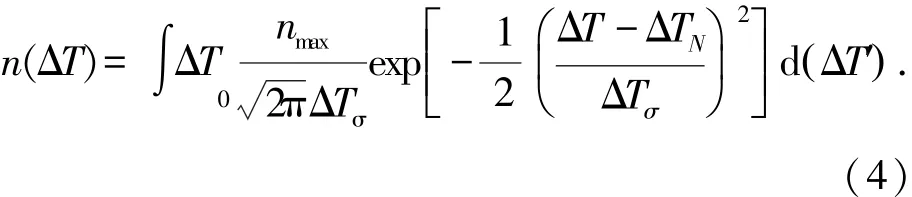
式中：n（ΔT）为在ΔT过冷度下的晶核密度；nmax为初始形核基底；ΔTN和ΔTσ分别为高斯正态分布的形核过冷度均值和形核过冷度方差.

过冷熔体在凝固过程中，壁面处受到异质形核的影响很大，这致使熔池壁面与熔池中心的形核基底数差异很大.因此，在模拟焊接熔池凝固组织过程中，采用两种不同的正态分布来控制晶粒的形核.

过冷熔体在过冷度的作用下一边形核一边长大.通常认为，晶粒是在热过冷（ΔTt）、成分过冷（ΔTc）和曲率过冷（ΔTr）的共同驱动下连续生长.根据Gibbs－Thompson方程可得二元合金枝晶生长过程中液／固界面平衡关系［16］为

式中：T∗为界面的平衡温度；T为界面处液相的初始温度；Γ为Gibbs－Thomson系数；ε为各向异性强度系数；θ0为晶体的择优生长方向；θ为液／固界面的法向与水平方向的夹角；mL为液相线斜率；C0和C分别为合金的初始浓度和液／固界面处液相中溶质浓度；K为液／固界面的曲率.液／固界面曲率可根据界面处固相份数（fS）梯度计算，

因此，液／固界面液相溶质的浓度可由下式得到：

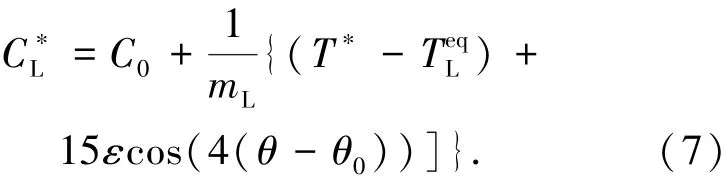
当界面处溶质浓度比液相中的高时，将产生浓度梯度，这促使界面处溶质向液相中扩散.随着溶质浓度的变化，界面元胞由糊状转变为固相，液／固界面不断向前推移，从而完成枝晶的生长过程.也就是说，界面处溶质的扩散是界面推移的诱因.单位时间（Δt）内，界面胞排除的溶质（ΔC）满足［17］

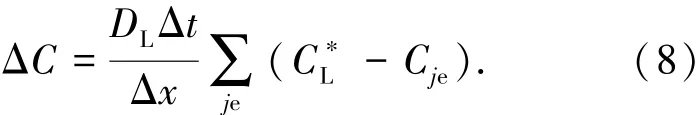
式中：DL为液相中溶质扩散系数；Δt为时间步长；Δx为微观单元尺寸；C∗L为界面液相溶质浓度；Cje为界面处液相邻胞中溶质浓度.

界面元胞内固相率的增量由下式控制：

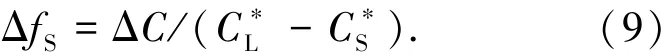
式中：C∗S为固相溶质浓度.在平衡生长状态下，二者之间满足C∗S＝k0C∗L，k0为溶质平衡分配系数.因此，在时间tN内，某一界面元胞j中固相率为

当0＜fjS＜1时，枝晶界面胞j持续生长；当fjS＝1时，界面胞由糊状转变为固相.转变完成时，凝固的界面胞将会捕捉与其相邻的液相元胞，使界面推进.凝固过程中，固相溶质浓度的确定是保证整个熔池溶质浓度守恒的关键，本文建立下式计算界面元胞j内的固相中溶质含量：

式中：CnL为tn时刻界面元胞j中的液相溶质浓度；ΔfnS为tn－1至tn时间内固相率增量；N为元胞j凝固所经历的的步数，n＝1时表示液相元胞j恰好转变为界面元胞.

式中：DL和DS分别为液相和固相中溶质扩散系数.

1.3 溶质再分配与扩散模型

枝晶生长过程中，随着液／固界面元胞中固相份数的增加，富余的溶质会被排出到元胞之外.根据溶质守恒定律，需将界面元胞排出的溶质添加到与其相邻的液相元胞之中.这样才能完成枝晶生长过程溶质的再分配过程.

由于学科竞赛的内容大多不是死记硬背的内容，而是从社会生活，时事政治选取方向来考查学生的综合能力，内容跨越各个课程和学科，具有较强的现实性和综合性。依靠过去死读书、读死书的学习方式显然无法适应这样的新型题目，因为不仅仅要运用已经学会的知识，还要对知识进行迁移和拓展，或者形成新的知识，或者将旧有知识重新建构在新的思维体系之中，形成新的解题思路，从而在竞赛中锻炼了文科学生的创新思维，激发了其创造力。

界面元胞溶质的再分配致使液相元胞间出现较大的浓度梯度，打破了溶质分布的动态平衡，加剧了溶质的扩散过程.对于二元合金，溶质的扩散对枝晶生长速度和形貌起着决定性作用.在过冷熔体的凝固过程中，各个元胞内的浓度随时间不断变化.根据菲克第二定律，溶质的二维扩散方程为

式中：Ci为溶质浓度，Di为扩散系数，下标i表示液相和固相两种状态.

2　模拟结果和讨论及实验验证

2.1 熔池凝固过程温度场模拟结果

模拟过程涉及的Fe－C二元合金基本热物参数如表1所示［18］.

表1　模拟使用的热物参数

将模拟区域划分为20×20个正方形的宏观网格，每个宏观网格由40×40个均匀的微观网格组成.微观网格尺寸为3 μm.溶质浓度取0.06%，熔池边缘散热速率为15 K·s－1.焊接熔池凝固1 s后的温度场分布模拟结果如图2（a）所示.从图2（a）可以看出三边散热时，底部温度下降最快.这使得模拟区域的等温线呈弧状分布；从图中还可以得出，从底边到顶部的散热边界，温度梯度不断减小，等温线的弧度逐渐增大.这一模拟结果与ansys有限元法模拟得出的焊接温度场结果吻合，如图2（b）所示.

图2　熔池凝固1 s时温度场

2.2 熔池内枝晶的竞争生长

熔池凝固过程枝晶的生长形貌和溶质浓度分布模拟结果如图3所示.

图3　熔池内枝晶竞争生长模拟结果（单位：μm）

图3（a）右侧衬度条中不同颜色代表着不同的晶粒，图3（b）和（c）右侧的衬度条为溶质浓度标尺，碳为溶质.从图3（a）可以看出，熔池凝固过程中在壁面上生长出大量的柱状晶，而熔池内部则形成粗大不均匀的等轴晶.这是因为在熔池不断降温的过程中，壁面附近由于异质形核数较多，在较低的过冷度下就能够形核并生长，并在枝晶生长过程中，相互竞争择优生长；而熔体内溶质均匀且异质核心数量少，需要较大的过冷度才能形核.形核后晶核受到的约束较小，故同时沿四个方向生长，直到被其它枝晶阻碍而停止生长，最终形成等轴的树枝晶.对比图3（a）、（b）可以得出，相邻柱状晶竞争生长过程中，竞争过程不是简单的枝晶臂接触阻碍而限制柱状晶的径向生长，而是枝晶臂撞击和溶质浓度共同作用而产生的现象.两者共同作用的结果是两相邻柱状晶间形成犬牙交错的二次枝晶臂.从图3（b）还可以看出，在凝固过程中，熔池散热边界附近的液相中溶质浓度远远高于绝热边和模拟区域中心的溶质浓度.这致使边界区域的液相溶质浓度的富集程度远高于其它区域.原因是过冷熔体凝固时，散热边界区域的过冷度较熔池内部和绝热边界大，枝晶的形核和生长速率较快；且快速生长排出的溶质由于受到相邻枝晶的阻碍而压缩了扩散空间和扩散距离.从图3（c）可以看出，柱状晶中固相溶质浓度沿轴向分布差异较等轴晶大；散热边界附近枝晶内溶质浓度最小，而熔池中心的等轴晶内溶质浓度则处于最高水平.

2.3 边缘散热速率对枝晶生长的影响

为了进一步分析散热速率对熔池凝固过程温度场和枝晶生长的影响，文中分别对边缘散热速率为15 K、30、60和80 K／s，凝固1 s后的枝晶形貌进行了模拟.

图4为不同散热速率作用下1 s后，沿图1（b）中AB直线方向的温度变化曲线.从图可以看出，当边界扩散速率一定时，熔池中的温度梯度沿直线AB不断减小.在到达模拟区域的绝热边界时，温度梯度趋于零；另外，模拟区域的温度梯度随着边界扩散速率的增加而加大.

图4　沿熔池中心线温度分布

为了定量分析散热速率对柱状晶的影响，文中对不同散热速率作用下柱状晶的平均长度进行了测定，结果如图5所示.从图中可以看出，柱状晶的长度随着散热速率的增长呈双曲线的形式减小，最终趋于一稳定值.

图5　不同热扩散速率下柱状晶的长度

2.4 形核基底数对枝晶生长的影响

焊接熔池冷却凝固过程中的形核数直接影响着凝固后的微观组织.为了分析不同形核基底数对熔池凝固过程枝晶数量和形貌的影响，分别模拟了散热速率为30 K／s，形核基底数为1×103、5×103、1×104和5×104，凝固1 s后熔池内枝晶的生长情况，结果如图6所示.从图可以得出，随着形核基底的增加，柱状晶数量基本稳定，而等轴晶的数量不断增多，分布范围逐渐扩大，尺寸有所减小.

图6　不同形核基底数下枝晶生长结果（单位：μm）

等轴晶数量随形核基底数的变化规律如图7所示.从图中可以看出，等轴晶数量的增幅随着形核基底数的增长而减小，这是由等轴晶的形核区域有限而引起的.

图7　形核基底对熔池中心等轴晶数的影响

2.5 实验验证

实验以低碳的HRBF400钢筋为原材料.钢筋直径ϕ为28 mm，采用X型坡口，以手工电弧焊焊接.焊接电流和电压分别取130 A和24 V，焊后空冷，冷却速率约为30 K／s.焊接完成后，测定的接头微观组织如图8所示.

图8　焊接接头组织形貌.

图8（a）为焊接接头熔合线附近处的组织形貌，从图中可以看出熔合线上焊缝一侧有大量的柱状晶形成；沿熔合线，柱状晶密度约为15个／mm，柱状晶向等轴晶转变（简称CET）过程中，越靠近熔池底部，柱状晶的轴向长度越小，这与图6（d）模拟得到CET结果中柱状晶的生长状况相符.图8（b）为焊缝中心的组织形貌.从图中可以得出，焊缝中有大量的大小相近的等轴晶存在，相邻晶粒被片状的铁素体隔开.晶粒直径约为150 μm，这与图6（d）模拟得到的等轴晶尺寸相近.

3　结论

1）熔池凝固过程中，温度梯度沿散热边界向绝热边界方向不断减小，而等温线弧度不断增大；熔池散热边界附近的液相中溶质浓度远远高于绝热边和模拟区域中心的液相溶质浓度；与此相反的是，散热边界附近枝晶内溶质浓度最小，而熔池中心的等轴晶内溶质浓度则处于最高水平.另外，柱状树枝晶内的固相溶质浓度沿轴向分布差异较等轴晶的大；

2）当边界扩散速率一定时，熔池中的温度梯度沿直线AB不断减小；在其它条件不变时，模拟区域的温度梯度随着边界扩散速率的升高而增加；随着形核基底数的增加，柱状晶数量基本不变，而等轴晶数量急剧增多，分布范围逐渐扩大，但尺寸有所减小；

3）散热速率30 K／s，形核基底数为5×104时，模拟得到的沿熔合线方向柱状晶密度和熔体内部等轴晶尺寸与实验结果相近；且模拟得到的柱状晶向等轴晶转变结果与实验得到的规律基本吻合.

参考文献：

［1］ PAVLYK V，DILTHEY U.Simulation of weld solidifi⁃cation microstructure and its coupling to the macro⁃scopic heat and fluid flow modelling［J］.Modelling and Simulation in Materials Science and Engineering，2004，12（1）：33－45.

［2］ YIN H，FELICELLI S D，WANG L.Simulation of a dendritic microstructure with the lattice Boltzmann and cellular automaton methods［J］.Acta Materialia，2011，59（8）：3124－3136.

［3］ REN Peng，ZHANG Wei，GUO Zitao，et al.Numerical simulation for deformation of multi⁃layer steel plates under underwater impulsive loading［J］.Journal of Harbin Institute of Technology（new series），2012，19（3）：68－72.

［4］ YIN H，FELICELLI S D.Dendrite growth simulation during solidification in the LENS process［J］.ActaMaterialia，2010，58（4）：1455－1465.

［5］ 袁训风，丁雨田.相场法模拟强各向异性作用下二元合金枝晶生长［J］.中国有色金属学报，2011，21 （9）：2216－2222.YUAN Xunfeng，DING Yutian.Phase⁃field simulation of dendrite growth for binary alloy with strong anisotropy［J］.The Chinese Journal of Nonferrous Metals，2011，21（9）：2216－2222.

［6］ 江鸿翔，赵九州.枝晶生长的三维元胞自动机［J］.金属学报，2011；47（9）：1099－1104.JIANG Hongxiang，ZHAO Jiuzhou.A three⁃dimension⁃al cellular automaton simulation for dendritic growth ［J］.Acta Metallurgica sinica，2011；47（9）：1099－1104.

［7］ 吕宝佳，康进武，黄天佑.基于cv⁃FDM法的铸件凝固过程热应力数值模拟［J］.材料科学与工艺，2010，18（6）：862－867.LU Baojia，KANG Jinwu，HUANG Tianyou.Numeri⁃cal simulation of thermal stresses of casting during so⁃lidification process by cv⁃FDM［J］.Materials Science and Technology，2010，18（6）：862－867.

［8］ LI Daming，LI Ruo，ZHANG Pingwen.A cellular au⁃tomaton technique for modelling of a binary dendritic growth with convection［J］.Applied Mathematical Modelling，2007，31（6）：971－982.

［9］ STEPHEN W.Computation theory of cellular automata ［J］Communications in Mathematical Physics，1984，96（1）：15－57.

［10］GANDIN C A，RAPPAZ M.A coupled finite element⁃celluar automaton model for the prediction of dendritic grain structures in solidification process［J］.Acta Metallurgica et Materialia，1994，42（7）：2233－2246.

［11］WANG W，LEE P D.A model of solidification micro⁃structures in nickel⁃based super⁃alloys：predicting pri⁃mary dendrite spacing selection［J］.Acta Materialia，2003，51（5）：2971－2987.

［12］许林，郭洪民，杨湘杰.元胞自动机法模拟铝合金三维枝晶生长［J］.铸造，2005，54（6）：575－578.XU Lin，GUO Hongmin，YANG Xiangjie.Simulating the three⁃dimensional dendritic growth of al alloy using the cellular automata method［J］.Foundry，2005，54 （6）：575－578.

［13］朱鸣芳，陈晋，孙国雄，等.枝晶生长的数值模拟［J］.金属学报，2005，41（6）：583－587.ZHU Mingfang，CHEN Jin，SUN Guoxiong，et al.Numerical modeling of dendritic growth［J］.Acta Metallurgica Sinica，2005，41（6）：583－587.

［14］HAKAN H，MATTI R.Microstructure evolution influenced by dislocation density gradients modeled in a reaction⁃diffusion system［J］.Computational Materials Science，2013，67：373－383.

［15］马瑞，董志波，魏艳红，等.镍基合金焊缝凝固组织演变过程模拟和仿真［J］.焊接学报，2010，31（7）：43－49.MA Rui，DONG Zhibo，WEI Yanhong，et al.Simula⁃tion of solidification microstructure evolution in molten pool of nickel base alloy［J］.Transactions of The Chi⁃na Welding Institution，2010，31（7）：43－49.

［16］BECKERMANN C，DIEPERS H J，STEINBACH I，et al.Modeling melt convection in phase⁃field simulations of solidification［J］.Journal of Computational Physics，1999（2），154：468－496.

［17］陈晋.基于胞元自动机方法的凝固过程微观组织数值模拟［D］.南京：东南大学，2005：27－30.CHEN Jin.Numerical simulation onsolidification microstructures using cellular automaton method［D］.Nanjing：Southeast University，2005：27－30.

［18］LUO Sen，ZHU Miao.A two⁃dimensional model for the quantitative simulation of the dendritic growth with cel⁃lular automaton method［J］.Computational Materials Science，2013，71：10－18.

（编辑 张积宾）

Simulation of solidification process of Fe－0.06%C alloy under non⁃uniform temperature field

ZHANG Min，WANG Qiang，XU Aiyan，XING Kui

（School of Materials Science and Engineering，Xi′an University of Technology，Xi′an 710048，China）

Abstract：The simulation model of macroscopic temperature field and dendritic growth，in which cellular automata⁃finite difference（CA－FD）methods and two kinds of scales are adopted，are combined to simulate the solidification process of Fe－0.6%C alloy in welding pool.According to the model，the influence of dendrite morphology and grain size with different boundary cooling rate and different nucleation basal are analyzed and discussed.To verify the simulation results，welding experiments are carried out.It is found that in the solidification process the temperature gradient decreases while isotherm curvature increases from the cooling side to the adiabatic side.Meanwhile，the solute concentration near the cooling side is much higher than that near the insulation boundary and in the center of the welding pool.Furthermore，the region of temperature gradient rises with the increase of cooling rate.As the nucleation substrate increases，the number of columnar crystals remains the same，while the amount of equiaxed crystals raise faster.The simulation results demonstrate the solidification process of welding pool and agree well with the experimental results.

Keywords：welding metallurgy；numerical simulation；weld pool；macro⁃micro model；microstructure；dendritic growth

通信作者：张 敏，E⁃mail：zhmmn＠xaut.edu.cn.

作者简介：张 敏（1967—），男，博士，教授，博士生导师.

基金项目：国家自然科学基金资助项目（51274162）；国家高技术研究发展计划资助项目（863计划）（2013AA031303）；陕西省基础研究计划项目（2012JM6003）.

收稿日期：2013－08－28.

doi：10.11951／j.issn.1005－0299.20150117

中图分类号：TG401

文献标志码：A

文章编号：1005－0299（2015）01－0101－07