Buck变换器拓扑指数改进算法及脆弱性分析

鲍春明，王春芳

（青岛大学 自动化工程学院，山东青岛266071）

0 引 言

脆弱性研究是全球变化及可持续性科学领域关注的热点问题和重要的分析工具，随着脆弱性研究受到越来越多的关注，对脆弱性的概念和评价方法的研究日益深入［1］。脆弱性这一概念源于对自然灾害的研究，在地学领域Timmer man P.（1981）首先提出了脆弱性的概念。目前脆弱性这一概念已被应用到很多研究领域，例如：灾害管理、生态学、公共健康、气候变化、土地利用、可持续性科学、经济学、工程学等。

在电力系统领域，电力系统脆弱性是用来描述系统在正常运行情况或各种随机因素的作用下系统承受干扰或故障的能力及系统不能维持正常运行的可能趋势及其影响［2］。专家学者们提出了各种各样的理论和模型来研究系统的脆弱性，包括：有向图矩阵分析法［3］、风险分析法［4］、故障链理论基础分析法［5］等。分子拓扑指数理论是建立在图的不变量基础之上的。它试图以这个拓扑不变量与分子的理化性质及生物分子的活性建立某种对应关系［6］。

文献［7］基于拓扑指数进行电网结构评价，利用拓扑指数的结论，分析了高压、中低压网络结构与性能之间的关系。文献［8］试图将拓扑指数计算模型引入到Buck变换器中来，具体方法是以拓扑指数找到Buck中的脆弱源，从而对Buck变换器做好稳定性保护，但是并没有考虑到电力电子拓扑的开关状态和占空比等特点，计算过程较为粗糙和简易。

本文首先介绍了拓扑指数的有关概念和结论，在拓扑指数和脆弱性概念的基础上，改进了Buck变换器拓扑指数的计算方法，通过对Buck变换器在连续工作模式（CCM）下的广义拓扑指数的计算，分析了它们的脆弱性，使得Buck变换器的脆弱性能够定量计算和分析。

1 拓扑指数及物理意义

1.1 基本概念［9，10］

定义1：K级非连接数P（G，K）

设边集合E有a条边，则K条边的子集总共有CKa个。在这些子集中，非邻接子集的数目称为集合E的K级非相邻连接数，记为P（G，K），并规定P（G，1）＝a（a是图中边的数目）。

定义2：拓扑指数TI（G）

图G的拓扑指数，边集合E的所有子集中，非邻接子集的数目（子集中所有边都非邻接），记为TI（G）。

式中，m＝|V|／2（|V|为偶数时）；m＝（|V|-1）／2（|V|为奇数时），|V|是节点的数目。

可以用图1来说明如何根据定义2计算一个已知图的拓扑指数。

图1 拓扑指数的计算示例图

如图1所示，该图有5个节点（v1，v2，v3，v4，v5），则|V|＝5；有8条边（ea，eb，ec，ed，ee，ef，eg，eh），即|E|＝8。与图1所对应的非邻接矩阵如公式（2）所示，行和列分别代表图1中的8条边，矩阵中的元素为1表示的是对应的边不相邻，为0表示的是相邻。

由图1和公式（2）可得，m＝（|V|－1）／2＝2，P（G，1）＝8，P（G，2）＝10，P（G，3）＝P（G，4）＝0，综上得到图1的拓扑指数为

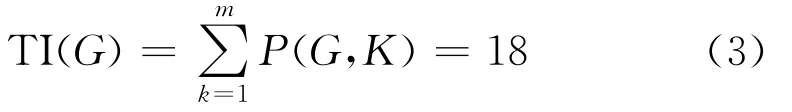
1.2 拓扑指数的物理意义

对于某一具体网络，拓扑指数的物理意义是度量该网络点和边（电路拓扑的节点和支路）连接均衡程度，即与每个节点相连接的边数是否一致。拓扑指数越大，则边分布越均衡，该网络的分散性越好。

由图2可知，示例网络a和网络b是具有相同的点数（7个）和边数（8条）的网络，并且点的分布一致，不同的是各个点之间的连接方式。直观地看，网络a中每个点连接的边数为2条或3条，比较均衡；网络b中点7连接的边数是5条，而点1和点4只有1条边与之相连，每个点连接的边数差别较大，不如网络b均衡度高。经过拓扑指数的计算：网络a的拓扑指数为33，网络b的拓扑指数为19。由此可知，网络的拓扑指数表征了网络的分散程度和均衡程度，拓扑指数越大，分散度越好，网络越均衡；反之，拓扑指数越小，分散度越差，网络越不均衡。

图2 示例网络a（左）和示例网络b（右）

对于拓扑指数的另一种理解：拓扑指数越大的网络，每个节点的重要性基本一样，安全性较好，某一点出现问题对于整个网络的影响相对较小。网络a中，点7断开，整个网络基本还是连通的；对于网络b而言，如果点7断开，整个网络几乎解体。

由此可见，一个网络是否安全可靠，与它的拓扑指数的大小有直接关系。电力电子电路可以抽象成一个电路网络，或称为电路拓扑，因此，使用拓扑指数来衡量电路网络的脆弱性，进而指导并优化电力电子电路的设计是可行的。

2 Buck变换器拓扑指数和脆弱性计算

2.1 Buck变换器的基本原理［11］

Buck变换器又称为降压斩波电路，其基本结构如图3所示，由输入电压Ui（等效为直流电压源Ui）、开关管S、二极管VD、电感L、电容C和等效负载电阻R构成。该电路存在电感电流连续和电感电流断续两种工作模式，本文只考虑电感电流连续工作模式下的情况。

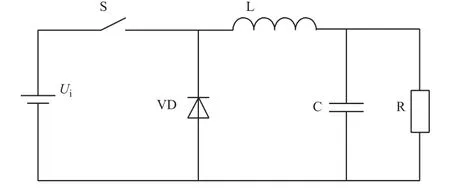
图3 Buck变换器的基本结构

Buck变换器在连续工作模式下有两个开关状态，如图4所示。开关状态1（S1）：开关管S导通，二极管VD关断。开关状态2（S2）：开关管S关断，二极管VD导通。定义占空比D为开关管导通的时间ton与开关周期Ts的比，即D＝ton／Ts，0≤D≤1。

2.2 Buck变换器的拓扑指数模型建立

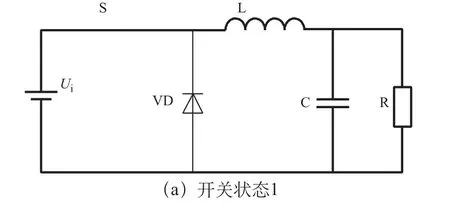
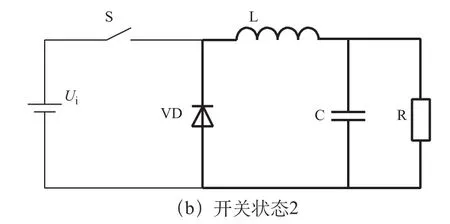
图4 Buck变换器的两种开关状态

Buck变换器的基本结构以及两个开关状态分别抽象为无向图。将输入电压Ui、开关管S、二极管VD、电感L、电容C以及等效输出电阻R抽象为节点V，它们之间的连线抽象为边E，得到其对应的无向图如图5所示。

根据拓扑指数的定义，计算图5中三个无向图的拓扑指数：

可知Buck变换器基本结构对应的拓扑指数是TI（Buck）＝49；

开关状态1对应的拓扑指数是TI（S1）＝15；

开关状态2对应的拓扑指数是TI（S2）＝9。

2.3 Buck变换器的拓扑指数计算与脆弱性分析

由模型可见，S1时的拓扑指数比S2时的拓扑指数大，由拓扑指数的物理意义可知，S1时的拓扑更加均衡，安全性更高。根据拓扑指数的概念，分析每个节点或元件在两个开关状态下对于变换器的影响，也就是不同结构性故障情况下变换器的脆弱性。得到拓扑指数计算式：

图5 Buck变换器基本结构

TI（A）=D×TI（S1，A）+（1-D）TI（S2，A）（4）式中，D表示Buck变换器的占空比，0≤D≤1；A表示某一节点或元件，如开关S、电阻R。另外，在拓扑中如果没有某一元件，则拓扑指数为零。如S1下没有二极管元件VD，则TI（S1，VD）＝0。此外，由于占空比的引入，广义拓扑指数的值可以是小数。

由此根据拓扑指数的定义和计算方法，得到不同元件在两个开关状态下的广义拓扑指数见表1。合和参数条件下，应尽可能保证二极管VD不发生故障。

图6 不同元件对变换器拓扑指数的影响图像

表1 元件在不同开关状态下的拓扑指数

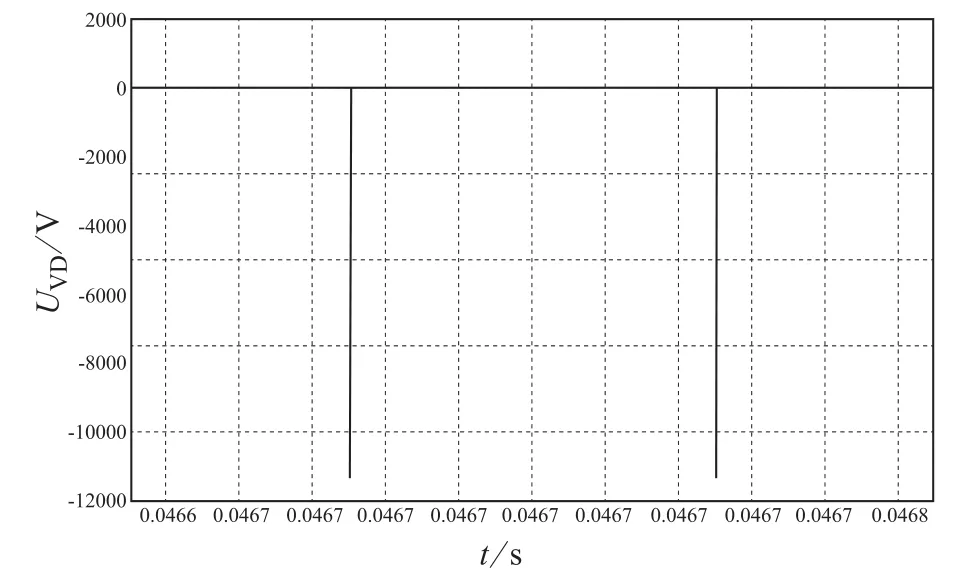
图7 Buck变换器二极管故障后的电压图像

根据公式（4）可得：

TI（S）＝7D，TI（Ui）＝5D，TI（VD）＝3－3D，TI（L）＝2D＋3，TI（C）＝3D＋3，TI（R）＝3D＋3。

不同元件对于变换器拓扑指数的影响是关于占空比D的函数，如图6所示。由图像可以看出：0≤D≤0.375时，在输入电压Ui发生损坏的情况下，拓扑指数最小，网络的均衡性差、可靠性降低，故Ui是脆弱源；0.375≤D≤1时，VD是Buck变换器的脆弱源。

使用Matlab对Buck变换器进行仿真，Buck变换器的输入电压为10 V，占空比为0.5，开关频率为20 k Hz，电感L为2.2 mH，滤波电容C为470μF，负载为1Ω。图7所示为二极管故障后的端电压。在实际应用中，Buck变换器经常会因为二极管的损坏，导致开关管承受电感L产生的过电压而损坏；二极管发生故障时，导致了电感等器件连锁损耗，说明二极管VD是Buck变换器的脆弱源。因此，在不同的应用场

3 结 论

本文将拓扑指数引入到电力电子变换器的脆弱性分析中，计算了在电感电流连续工作模式下Buck变换器不同开关状态的拓扑指数，分析了由占空比决定的广义拓扑指数的特征；通过对Buck变换器的广义拓扑指数的计算，使Buck变化器脆弱性能定量计算和分析。引入占空比这一参数，并且考虑到Buck变换器不同开关状态的影响，使得拓扑指数的计算更加细化，利于分析。该拓扑指数计算方法对于非隔离型变换器拓扑均适用，但对于该变换器的电感电流断续工作模式（DCM）以及含有变压器的隔离型变换器拓扑，计算方法还需改进。

［1］ 李 鹤，张平宇，程叶青.脆弱性的概念及其评价方法［J］.地理科学进展，2008，27（2）：18-25.

［2］ 魏震波，刘俊勇，朱国俊，贺星棋，龚 薇.电力系统脆弱性理论研究［J］.电力自动化设备，2009，29（7）：38-43.

［3］ Ivan J Sacks.Digraph Matrix Analysis［J］.IEEE Reliability Society，1985，34（5）；437-446.

［4］ Alexis Kwainski.Technology Planning for Electric Power Supply in Critical Events Considering a Bulk Grid，Backup Power Plants，and Micro－Grids［J］.IEEE System Journal，2010，4（2）：167-178.

［5］ Ansi Wang，Yi Luo，Guang Tu，Pei Liu.Vulnerability Assessment Schemefor Power System Transmission Networks Based on the Fault Chain Theory［J］.IEEE Transa.On Power Systems，2011，26（1）：420-450.

［6］ 杨 锋，罗明道.分子拓扑指数的理论和应用［J］.自然杂志，1997，（1）：50-53.

［7］ 张李盈，范明天，田喜峰.基于拓扑指数的电网结构评价［J］.山东电力高等专科学校学报，2008，（1）：67-70.

［8］ 张桂东，张 波，丘东元，肖文勋.Buck变换器的拓扑指数及脆弱性分析［J］.电源学报，2012，（06）：19-22.

［9］ 兰家隆，刘 军.应用图论及算法［M］.成都：电子科技大学出版社，1995.

［10］卜月华.图论及其应用［M］.南京：东南大学出版社，2002.

［11］裴云庆，杨 旭，王兆安.开关稳压电源的设计和应用［M］.北京：机械工业出版，2011.