四旋翼无人飞行器反步法的控制

陈奕梅，陈增辉，修春波

（天津工业大学电气工程与自动化学院，天津 300387）

四旋翼无人飞行器反步法的控制

陈奕梅，陈增辉，修春波

（天津工业大学电气工程与自动化学院，天津 300387）

四旋翼无人飞行器是一种典型的六自由度的非线性、强耦合、欠驱动系统.针对四旋翼无人飞行器Qball-X4受控模型的复杂非线性问题，从实际应用的角度出发，提出了一种在定点悬停情况下忽略偏航角变化的模型简化方法，有效地解决了内外环约束条件的求解问题，并基于此模型设计了一种基于反步法的渐近稳定控制器.仿真结果表明：所设计的控制器能有效地实现定点飞行，同时，也验证了所建立的简化模型的合理性.

四旋翼无人飞行器；欠驱动系统；反步算法；渐近跟踪

四旋翼无人飞行器能够完成悬停、低速飞行、垂直起降和室内飞行等动作，具有固定翼无人机无法比拟的优势.同时，以其制造精度要求低、稳定性好、陀螺效应弱的特点，在军用、民用、商用等领域存在着强大的应用潜力，成为近年来的一个研究热点问题[1].在飞行器的非线性控制中，反步法（backstepping）作为一种有效的控制方案受到了关注.文献[2-3]都使用了反步法得到了较好的仿真效果，但在控制器中引入了代数环.文献[4-5]虽然克服了代数环，但姿态和位置的超调值略大，控制效果不理想.因此，这些仿真结果都很难用于实际控制系统.本文以Qball-X4四旋翼无人飞行器为研究对象，从控制器的实用角度出发，根据实验中飞行器定点飞行的特点，提出了一种模型简化方法，在该模型的基础上，得到了控制系统的内外环的约束条件，并设计了基于反步法的稳定控制器，最后在实验中验证了约束条件的合理性.同时，在反解电机PWM值的过程中，加入一阶低通滤波环节，防止四旋翼无人飞行器在实际飞行过程中因电机PWM值畸变而出现跑飞现象.

1 四旋翼无人飞行器建模

四旋翼无人飞行器是一个典型的四输入六输出的非线性、强耦合、欠驱动系统，呈刚性的十字交叉结构，其4个电机分别均匀对称安装在十字结构的末端.飞行中通过调节4个电机的转速来控制4个电机的升力，以完成飞行器各个飞行姿态的转换.4个电机分左右、前后2组，且2组电机转向相反[6].图1为实验室使用的QUANSER公司的Qball-X4飞行器的实物图.

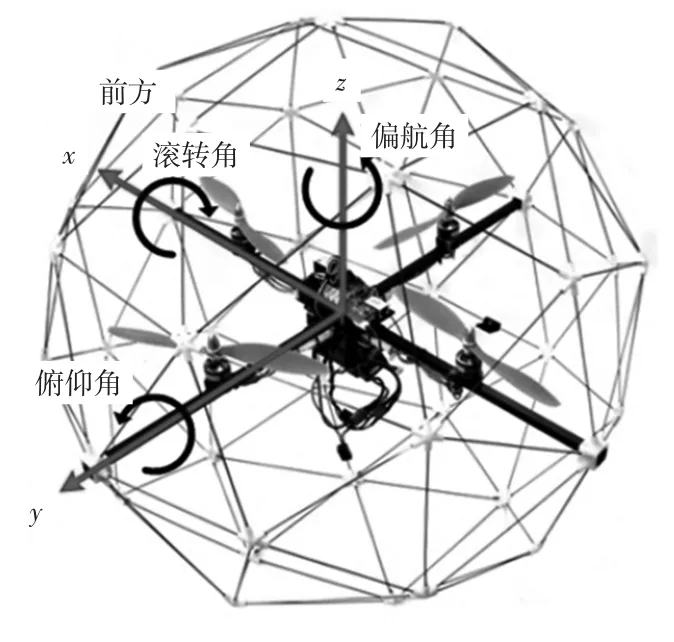
图1 Qball-X4四旋翼无人飞行器Fig.1 Qball-X4 quadrotor unmanned aerial vehicle

在图中机体坐标系中，定义θ为俯仰角（Pitch）、φ为滚转角（Roll）及ψ偏航角（Yaw），并且，φ∈（-仔/2，仔/2），θ∈（-仔/2，仔/2），ψ∈（-仔/2，仔/2）[7].结合 Qball-X4四旋翼无人飞行器电机结构和力学知识可知：

式中：U1为电机产生升力fi（i=1，2，3，4）的合力；K为电机模型的正增益系数；ω为电机的带宽；ui（i=1，2，3，4）为电机PWM输入；s为频域，s=jwt.

考虑到四旋翼无人飞行器的飞行特点，从简化问题复杂性的角度出发，文献[8]提出以下假设：

（1）视飞行器为一个刚体，结构均匀对称；

（2）在四旋翼无人飞行器飞行过程中，忽略旋翼的弹性形变及震动；

（3）机体坐标系原点与四旋翼无人飞行器质心原点完全重合；

（4）认为地面坐标系为惯性坐标系，忽略地球的曲率及自转；

（5）考虑室内无风和慢速飞行，忽略风的阻力系数.

基于上述假设，建立常规四旋翼无人飞行器的数学模型[9]；

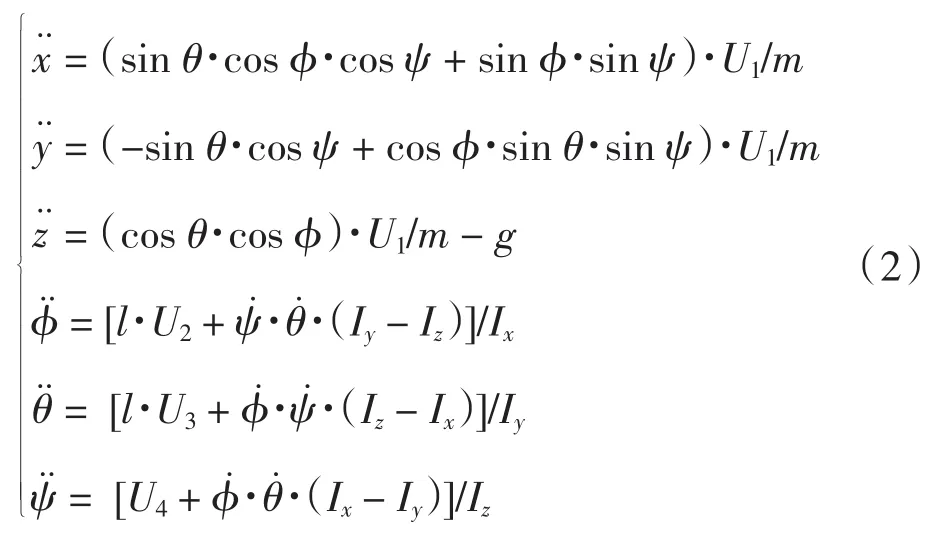
式中：（x，y，z）代表飞行器相对于地面直角坐标系下的位置；m为飞行器的质量；Ix、Iy、Iz分别为飞行器本体绕机体坐标系x、y、z轴的惯性矩；l为机体中心到电机中心轴的长度.为了便于仿真和下面控制器的设计，引入U2=f4-f2，U3=f3-f1，U4=Ky·（u1+u3-u2-u4）与式（1）中的U1共同构成4个模拟输入量[10].

由Qball-X4四旋翼无人飞行器结构严格对称的特点可知，姿态环中姿态角ψ通道是相对独立的，为了更好地维持飞行器飞行的姿态稳定，给期望的ψcmd=0，由于在定点飞行过程的实验中，实际偏航角始终在期望值附近变化，因此ψ≈0.在此基础上，对飞行器的数学模型进行合理简化，简化后的四旋翼无人飞行器模型为：

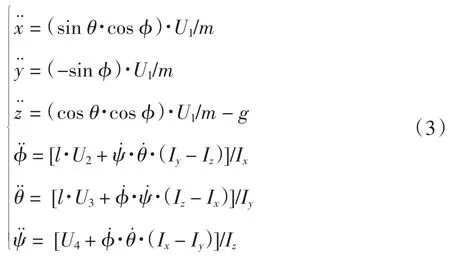
2 基于Backstepping控制器的设计

2.1 模型变换

由上述数学模型可知，姿态角和角速度不依赖线运动，而线运动的位置空间变化却依赖角运动，角运动与线运动之间存在着半耦合的关系[11].因此，将整个四旋翼无人飞行器控制系统分为内环（姿态环）和外环（位置环），控制器的设计包含了对姿态环和位置环2个子控制器的设计[12].系统的结构控制图如图2所示.其中：（xcmdycmdzcmd） 为期望的位置输入；（φcmdθcmdψcmd）为期望的姿态输入.

图2 四旋翼无人飞行器系统控制框图Fig.2 Control system block diagram of quadrotor unmanned aerial vehicle

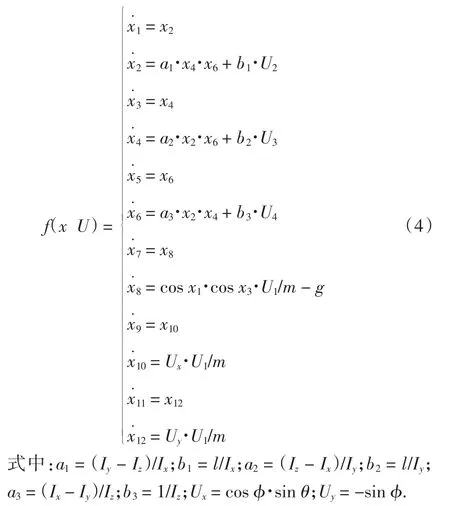
2.2 四旋翼无人飞行器姿态环控制器设计

由（4）式可得滚转通道方程的表达式为：

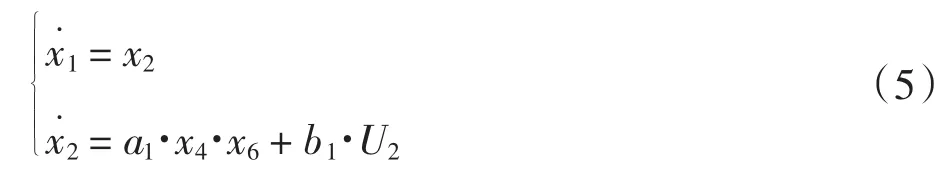
给定期望滚转角φcmd=x1d，定义误差变量e1=x1dx1，等式两边同时求导得：

引入虚拟控制量α1，定义误差变量

进一步，选取Lyapunov函数

沿系统（5）求导得：

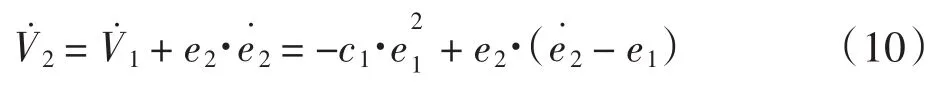
将（5）、（6）、（8）式分别代入（10）式得到：

取

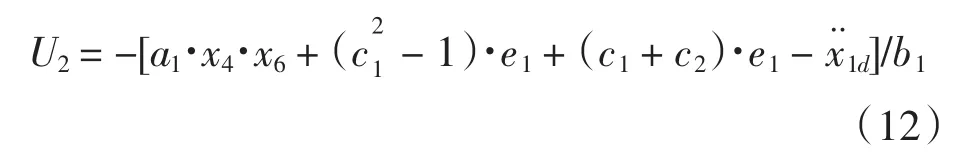
式中：c2＞0，得到对于所有的e1≠ 0，e2≠0，V˙2＜0.由Lyapunov稳定性可知，系统（5）在控制量（12）式的作用下渐近稳定.

同理，取期望俯仰角θcmd=x3d，期望偏航角ψcmd=x5d，且定义e3=x3d-x3，e5=x5d-x5，则可以求得：

俯仰通道：

偏航通道：

2.3 四旋翼无人飞行器位置环控制器设计

Z通道方程表达式为：

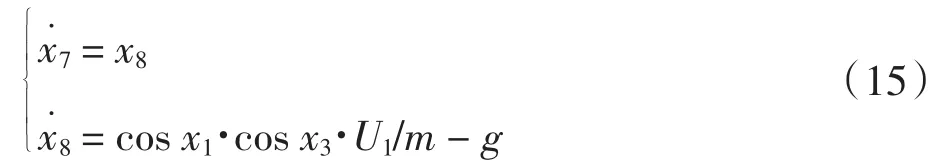
令期望高度zcmd=x7d，引入误差变量e7=x7d-x7，对误差变量求导得

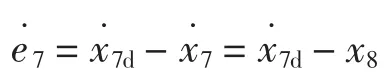
取虚拟控制量α7，并定义

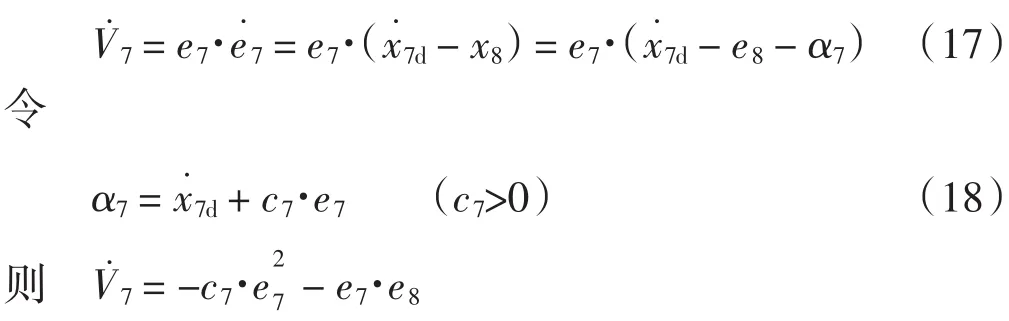
进一步，取Lyapunov函数

将其沿（15）式求导，得：

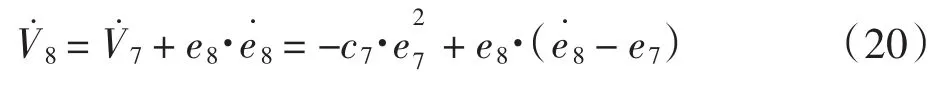
将

（15）、（16）、（18）式带入（20）式得到：

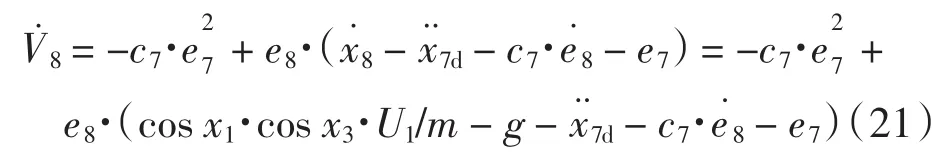
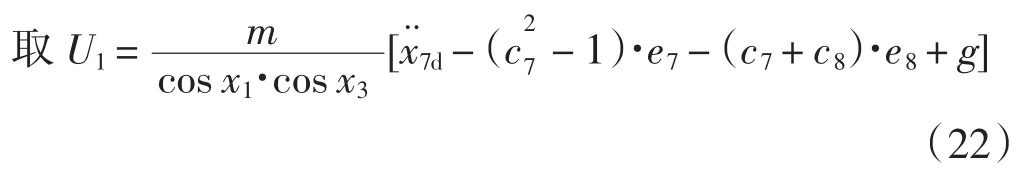
式中：c8>0，得到

在平衡点外负定，则系统（15）渐近稳定.

取X位置通道期望xcmd=x9d，Y位置通道期望ycmd=x11d，且定义e9=x9d-x9，e11=x11d-x11，则同理可以求得：

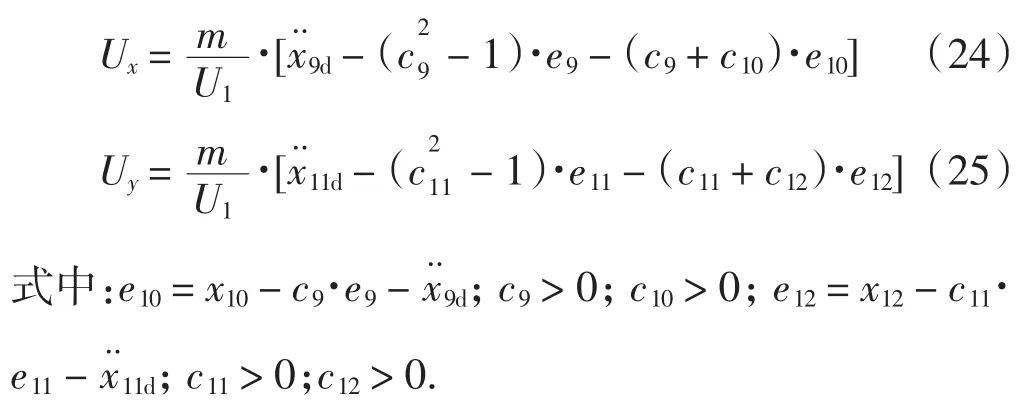
2.4 非线性约束条件

由上面的设计过程可知，整个控制器的设计分为了姿态控制器和位置控制器2部分，内环姿态控制器作用是调整四旋翼无人飞行器在飞行过程中姿态角的变化，外环位置控制器的作用是控制飞行器按照期望的轨迹飞行.飞行器的6个期望位姿中，已知条件只给出其中的4个，即xcmd、ycmd、zcmd和ψcmd.而另外2个期望的姿态角θcmd和φcmd是通过如下内环与外环的之间的非线性约束条件[13]得到.

反解推导出期望姿态角为：

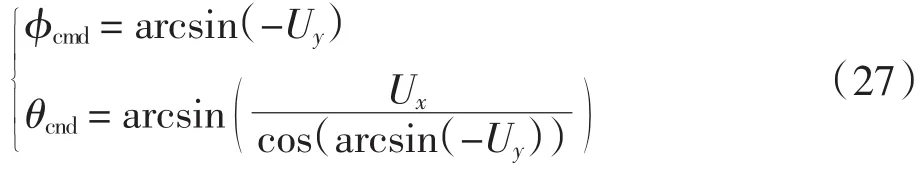
3 实验仿真与结果分析

基于上述设计过程，搭建仿真模型，为了验证模型简化后反步法控制算法的有效性和可行性，进行了Matlab仿真.设定四旋翼无人飞行器飞行的起始位置坐标（x y z）=0 m，起始姿态角（φ θ ψ）=0 rad，期望位置坐标为（xcmdycmdzcmd）=（1 1 1）m，期望偏航角ψcmd=0 rad，仿真时间t=10 s.模型中的其他参数如表1所示.

表1 物理常量的参考值Tab.1 Physical constants of reference value

控制器在（22）式、（12）-（14）式的作用下，四旋翼无人飞行器一系列仿真结果如图3—图6所示.

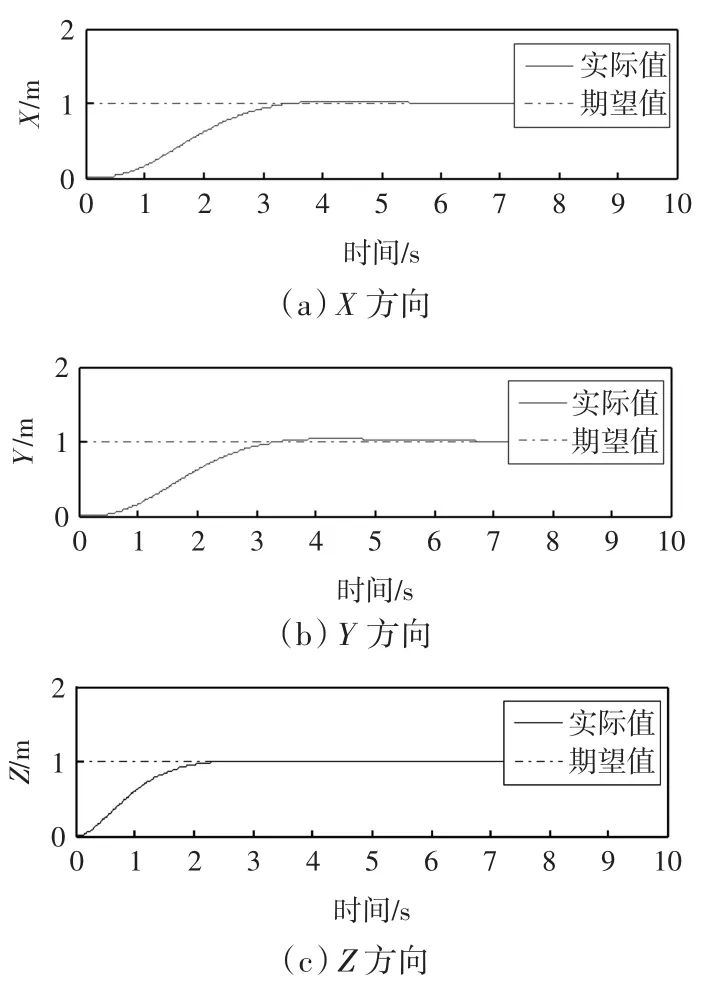
图3 位置仿真结果Fig.3 Simulation results of position

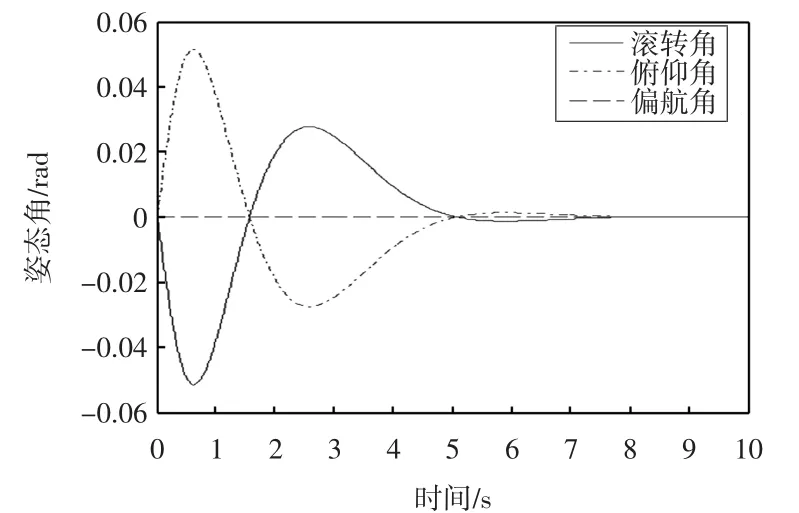
图4 姿态角仿真结果Fig.4 Simulation results of attitude

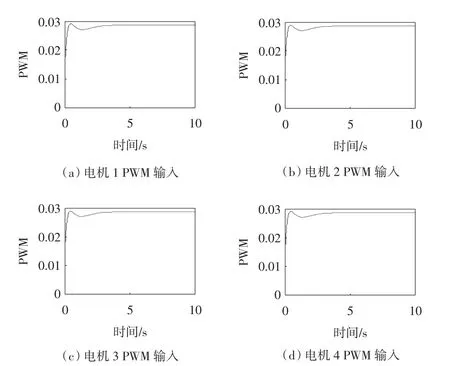
图5 电机PWM仿真结果Fig.5 Simulation results of PWM

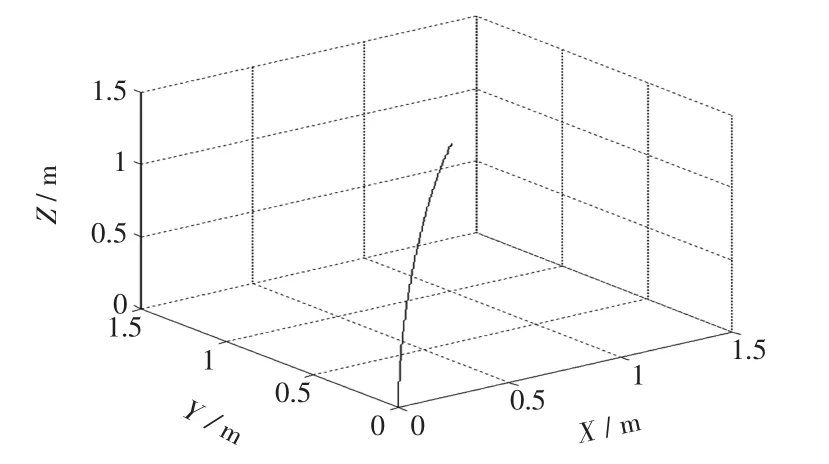
图6 四旋翼无人飞行器飞行轨迹Fig.6 Flying trajectory of quadrotor UAV

由多次试验结果对比可知，当ci的值越大，（i=1，2，3，4，5，6，7，8，9，10，11，12），位置和姿态角的响应速度越快，同时，位置和姿态角的超调量也将越大.考虑实际飞行中的安全因素，取ci=1.5，cj=1，（i=1，2，3，4，5，6，7，8；j=9，10，11，12），图3和图4所示的位置和姿态角的超调量较小，在仿真时间内，都能够趋于期望目标，从而证明了反步法控制算法在该四旋翼无人飞行器模型中的有效性和稳定性.

进一步，从图4中可以看出，偏航角始终保持在平衡点位置，即ψ≈0，从而验证了模型简化条件的合理性.

在实际飞行过程中因为电机PWM值畸变，很容易导致飞行器跑飞的现象.从安全角度考虑，在反解求电机PWM的过程中，给4个虚拟输入都加了1个一阶低通滤波环节5/（s+5），得到的图5中4个电机PWM曲线才更加平滑.

从图6中可以看出，四旋翼无人飞行器在定点飞行过程中的轨迹是比较平滑的，符合实际飞行的需求.

4 结语

本文以四旋翼无人飞行器为研究对象，在一定合理的假设前提下，对四旋翼无人飞行器在运动学和动力学方面展开分析，并建立了四旋翼无人飞行器的常规数学模型，在实际控制过程中进一步简化模型，利用Lyapunov稳定判据，结合Backstepping控制算法对控制器进行设计，并对四旋翼无人飞行器的位置和姿态进行了仿真.仿真结果显示Backstepping控制算法可以满足四旋翼稳定性要求.下一步将对该控制器用于飞行器实物进行性能测试.

[1]王福超.四旋翼无人飞行器控制系统设计与实现[D].哈尔滨：哈尔滨工程大学，2013.

[2]BAVISKAR A，FEEMSTE M，DAWSON D，et al.Tracking control of an underactuated unmanned underwater vehicle[C]// Proceedings of the American Control Conference.Portland：[s.n.]，2005：4321-4326.

[3]DAS A，LEWIS F，SUBBARAO K.Backstepping approach for controllingaquadrotorusinglagrange form dynamics[J].Journal of Intelligent Robotic System，2009，56（1/2）：127-151.

[4]赵元伟，卢京朝.四旋翼飞行器的建模及基于反步法的控制[J].科学技术与工程，2013，34：10425-10430.

[5]黄兵兵，李春娟，何墉，等.基于反步法的微型四旋翼欠驱动控制[J].洛阳理工学院学报：自然科学版，2013（2）：56-61.

[6]黄依新.四旋翼飞行器姿态控制方法研究[D].成都：西南交通大学，2014.

[7]MADANI T，BENACLEGUE A.Backstepping control with exact 2-sliding mode estimation for a quadrotor unmanned aerial vehicle[C]//Proceeding of IEEE Conference on Intelligent Robts and Systems.San Diego：IEEE，2007：141-146.

[8]黄溪流.一种四旋翼无人直升机飞行控制器的设计[D].南京：南京理工大学，2010.

[9]BOUABDALLAH S，SIEGWART R.Backstepping and sliding-mode techniques applied to an indoor micro quadrotor[C]// International Conference on Robotics and Automation.Barcelona：[s.n.]，2005：2247-2252.

[10]AL-YOUNES Younes，JARRAH M A.Attitude stabilization of qua-drotor UAV using backstepping fuzzy logic&backstepping least-mean-squarecontrollers[C]//Proceeding of the 5th International Symposium on Mechatronics and Its Applications. Amman：Inst of Elec Eng，2008：10-15.

[11]刘焕晔.小型四旋翼飞行器飞行控制系统研究与设计[D].上海：上海交通大学，2009.

[12]GENG Qingbo，SHUAI Huan，HU Qiong.Obstacle avoidance approaches for quadrotor UAV based on backstepping technique[C]//Proceeding of Chinese Control and Decision Conference.Guiyang：[s.n.]，2013：3613-3617.

[13]凌金福.四旋翼飞行器飞行控制算法的研究[D].南昌：南昌大学，2013.

Backstepping control of quadrotor unmanned aerial vehicle

CHEN Yi-mei，CHEN Zeng-hui，XIU Chun-bo
（School of Electrical Engineering and Automation，Tianjin Polytechnic University，Tianjin 300387，China）

Quadrotor unmanned aerial vehicle（UAV）is a typically nonlinear，underactuated and highly-coupled dynamical system with six degree of freedom.According to the complex nonlinear problem of Qball-X4 UAV controllable model，a model simplification method is proposed by ignoring the influence of the angle change of yaw when aerial vehicle keeps hovering at a certain point，and the problem of the constraints between inner and outer loops is effectively solved.A asymptotically stable controller is also designed through the backstepping algorithm based on the model.Numerical simulations are provided to illustrate the effectiveness of the proposed method，simultaneously，the rationality of the simplified model is also verified.

quadrotorunmannedaerialvehide（UAV）；underactuatedsystem；backsteppingalgorithm；asymptoticaltracking

TP271.72；TM755；V249.122

A

1671-024X（2015）05-0032-05

10.3969/j.issn.1671-024x.2015.05.007

2015-06-12

天津市应用基础及前沿技术研究计划项目（14JCYBJC18900）

陈奕梅（1972—），女，博士，副教授，硕士生导师，主要研究方向为机器人控制技术.E-mail：chenyimei@tjpu.edu.cn