多元测量系统分析在机器视觉中的应用

施亮星，任海佳，肖 航

（天津大学管理与经济学部，天津 300072）

多元测量系统分析在机器视觉中的应用

施亮星，任海佳，肖 航

（天津大学管理与经济学部，天津 300072）

为解决一元测量系统分析方法无法准确评价机器视觉系统能力的问题，运用多元测量系统分析方法，通过探讨机器视觉系统的特点，建立其测量值的变异源模型，并通过交叉试验和多元方差分析（MANOVA）方法估计各变异源的方差协方差矩阵，据此计算它的重复性和再现性指标，给出对机器视觉系统的评价.结果表明：将这些方法运用到芯片规格测量的具体案例中，并与一元方法进行对比，取得了较好的效果.

多元测量系统；机器视觉系统；重复性；再现性

近年来，机器视觉系统（machine vision system，MVS）被广泛地用于各个领域，并积累了丰富的学术研究成果.Megahed等[1]总结了医学和工业上图像数据与控制图结合的研究案例，并探讨了这些方法的优点和不足.Huang等[2]提出了基于神经网络和图像处理技术，检测农产品质量并进行归类的方法.王宝锋等[3]将机器视觉与雷达结合进行车辆识别，弥补了单一传感器在车辆识别中的不足.贺继林等[4]利用机器视觉进行工业操作导航，实现了工业探测机器人自主作业的功能.与人眼相比，机器视觉系统的主要优势在于：提高定位识别的效率、精度和稳定性，消除不同测量个体带来的差异，减少识别损耗等.然而，在使用机器视觉系统采集的数据进行质量评定或生产过程监控之前，应当对机器视觉设备进行测量系统分析，以保证测量数据的有效性.

目前，机器视觉领域的测量系统分析研究比较少. Kachitvichyanukul[5]在检测食品表面颜色缺陷时，运用重复性再现性方法，分析测量系统的波动.Majeske[6]在轴承尺寸测量实例中，通过分离相同零件、相同测量维度在不同测量位置的波动，探讨了机器视觉领域测量系统分析的特殊性.然而，这些应用仍然局限在一元范畴.机器视觉系统往往同时测量产品多个维度质量特性，当这些质量维度存在相关性时，一元方法不能综合、准确地评价测量系统能力.为解决该问题，本文结合芯片规格检测的具体案例，探讨多元测量系统分析方法在机器视觉中的应用.

1 文献综述

测量系统分析是指运用统计学的方法识别测量系统中的波动源，并评估它们对测量值的影响，最后判定测量系统是否合乎要求[7].Burdick[8]和Montgomery[9]总结并提出了测量系统能力研究的3个目的：①确定观察到的总波动有多少来源于测量系统；②分析变异来源，分离测量系统误差；③评价测量系统的能力.

现有的测量系统能力研究大多是一元的，即假设量具每次只测量产品的一个质量特性.美国汽车工业行动集团（AIAG）介绍了一元测量系统分析的评价指标，包括%P/T、%R&R、SNR和DR，这4个指标是判断测量系统能力是否充足的依据.对于这4个指标，Woodall[10]进行了更加详细和深入的探讨.

然而，当测量系统同时测量被测物体多个质量特性时，这些质量特性往往存在相关性，需要进行多元分析来评价测量系统能力.

近些年，多元测量系统研究引起了国内外学者的重视.Sweeney[11]结合实际案例，给出了分析二元测量系统能力的方法.Voelkel[12]研究了公差是一个圆的时候，二元数据重复性和再现性问题，并系统地比较了该方法与一元方法的不同.Majeske[13]以车身面板四元测量数据为研究对象，利用多元方差分析（MANOVA）方法，将测量系统分析从一元推广到多元，构建了基于面积比或体积比的多元测量系统评价指标.吴小芳等[14]提出基于向量的多元测量系统能力评价指数，来修正Majeske[13]的方法中椭球体积不变但测量系统能力发生变化的问题.

2 多元测量系统分析方法

典型的多元测量系统分析试验设计中，o个操作者对p个零件的n个质量特征进行s次重复测量，测量值M是一个n维的多元正态响应：

若Mijk表示第i个零件被第j个操作者第k次测量得到的结果向量，则多元测量系统分析的模型可以表示为：

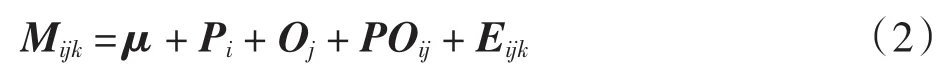
式中：i=1，…，p；j=1，…，o；k=1，…，s；μ=[μ1，μ2，…，μn]代表均值向量；Pi～N（0，ΣP）表示零件效应；Oj～N（0，ΣO）代表操作者效应；POij～N（0，ΣPO）代表零件操作者交互效应；Eijk～N（0，ΣE）代表随机效应.这些协方差矩阵有如下关系：

多元测量系统分析的评价指标主要有2个，%P/ Tm和%R&Rm[14]：

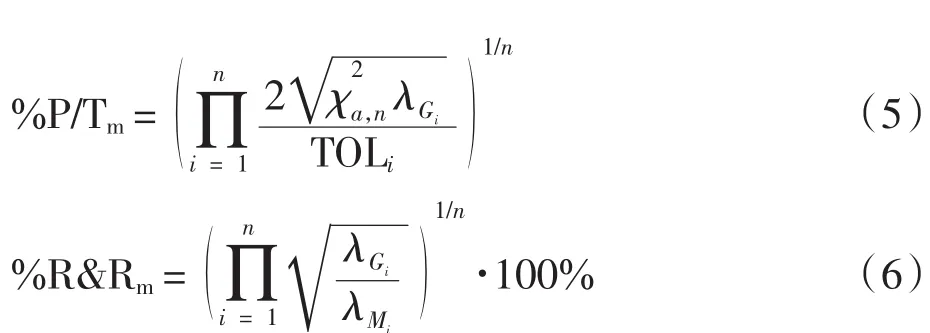
式中：λG、λM分别为ΣG和ΣM的特征值；TOLi是第i个维度的公差；χ2a，n为以n为参数的卡方分布的上α分位点的值.

AIAG[10]给出了这2个指标的评价标准：如果%P/ Tm和%R&Rm均小于10%，说明测量系统能力充足；如果二者的值在10%～30%之间，则要根据测量对象的重要程度来判断测量系统是否可以被接受；如果二者的值大于30%，则说明测量系统能力不足，必须改进.

3 芯片规格机器视觉测量系统实例研究

在工厂A中，一台机器视觉设备被用来自动测量芯片的长和宽.与显微镜相连的CCD摄像机自动对随机撒在载物台上的多个芯片拍照.计算机对放大的照片进行增强、切割等处理，并利用漫水填充和最大连通区域等算法，自动识别芯片，测量其长和宽.

传统的一元测量系统分析假设量具只测量被测物体一个维度的质量特性，如芯片长度.然而，芯片规格机器视觉系统同时测量芯片的长和宽，且历史数据显示，这两个变量的测量值是具有相关性的.因此，应当将这两个变量看成一个多元响应，进行多元测量系统分析.

3.1 波动源识别

在芯片规格机器视觉测量系统中，主要的波动源包括：芯片在视野中的位置，芯片的放置角度以及不同芯片本身的波动.为了捕获位置因素带来的波动，显微镜视野被平均分成16等份，即4行4列，这便形成了一个4水平的行效应和4水平的列效应.分成16个区域是平衡试验可操作性和试验准确度之后的选择.对于放置角度，考虑到可操作性，0，被选作为测试水平.为了估计芯片本身的波动，从生产线上随机抽取8个芯片进行试验.该操作系统自动化程度很高，操作者对测量系统的影响可以忽略不计[15]，同样，也暂不考虑各因素的交互作用.

3.2 模型与实验设计

典型的测量系统分析模型（公式2）把操作者和零件作为波动源，然而，在芯片规格机器视觉测量系统中，波动源发生较大的变化，需要将放置位置、放置角度对测量结果的影响.此处用到的统计模型可以表示为：

本文利用全因子交叉试验，让每个零件在每行、每列、每个方向上各被重复测量3次，来估计各波动源的协方差矩阵.其中：i，j=1，2，…，r；q=0，π/4，π/2，3π/4；p=1，2，…，np；k=1，2，…，ns.r=4表示行、列、方向的数量，np=8表示零件数，ns=3表示在每个组合下的重复次数.Mijqpk=[Mijqpk(length)，Mijqpk(width)]是测量值向量；μ=[μlength，μwidth]代表均值向量；Ri～N（0，Σrow）代表行效应；Cj～N（0，Σcolumn）代表列效应；Aq～N（0，Σangle）代表方向效应；Pp～N（0，Σpart）代表零件效应；Eijqpk～N（0，ΣE）代表随机效应.

利用多元方差分析的方法计算各波动源的均方，这些均方的线性组合被用来计算各协方差矩阵：

与常用的操作者-零件模型类似，这些协方差分量之间有如下关系：

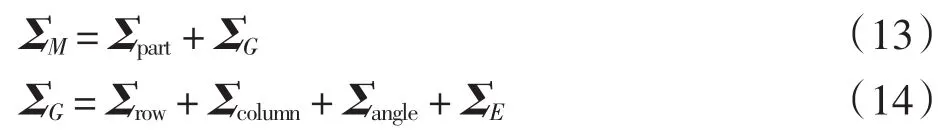
计算ΣM与ΣG的特征值，代入公式（5）、（6）中，就可以得到最终的测量系统评价指标值.

3.3 结果与讨论

本例中使用的是1005芯片，其规格为1 000 μm× 500 μm，长度和宽度的公差分别为100 μm和50 μm.按照2.2中的模型和方案进行数据采集，并对采集到的数据进行分析.

长度和宽度测量值、测量误差相关性分析结果如表1所示.

表1 相关性检验Tab.1 Correlation test

从表1中可以看出，芯片长和宽的测量值Pearson相关系数为0.833，该系数显著为真，表明芯片长和宽的测量值存在较大相关性.同理，长和宽的测量误差也存在相关性.因此，应该对该测量系统进行多元能力评价.

运用多元方差分析的方法处理数据，并根据式（8）—式（12）计算各协方差分量矩阵，结果如表2所示.

表2 多元方差分析的协方差矩阵Tab.2 Covariance matrix of MANOVA

根据公式（13）（14），可以得到ΣM与ΣG，并计算其特征值λG与λM，结果如表3所示.

表3 总误差、测量误差与特征值Tab.3 Total error，measurement error and eigenvalue

根据公式（5）和公式（6），可以计算出多元测量系统的评价指标.其中：%P/Tm值为11.40%；%R&Rm为15.57%.

为进行比较，对长和宽分别进行一元测量系统分析，并计算其几何平均数，结果如表4所示.

长和宽的测量误差和测量值均不相关时，多元测量系统评价结果是一元结果的几何平均数.%P/Tm（11.40%）要小于相应的一元几何平均数（12.32%），这是由测量误差的相关性导致的.比如，由于显微镜边缘形变造成的测量误差同时影响长和宽，且在2个维度上的影响是相关的.当把长和宽看成2个独立的一元响应时，由该原因导致的测量误差，其长和宽的相关部分被计算了2次，因此，%P/T的一元几何平均数要大于多元指标%P/Tm.又从表1中可知，本例长和宽的测量误差相关系数为0.615，存在相关性，但相关性较弱，所以一元几何平均数只比多元指标大了1%.

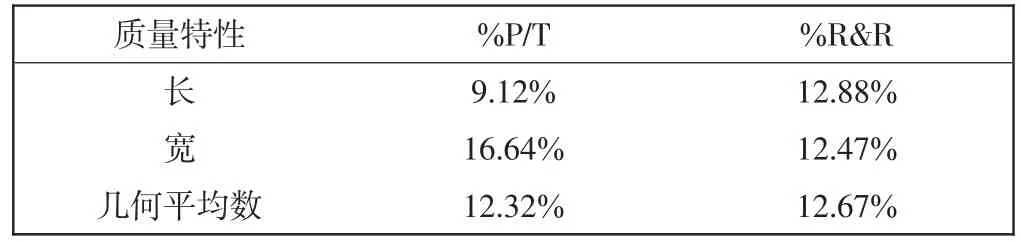
表4 一元测量系统分析结果Tab.4 Result of univariate ANOVA

%R&Rm和%R&R均是测量误差波动与总测量值波动之比.与一元相比，多元分析考虑了相关性，因此测量误差和测量值的波动都变小.但由于测量值的相关系数更大（0.833），相关性更高，分母比分子缩小的更快，所以多元指标%R&Rm要大于一元几何平均数.

由此可见，多元指标考虑了各维度数据的相关性，对测量系统评价更加准确.本例中，多元评价指标%P/ Tm和%R&Rm都远小于30%，由此判定，该测量系统能力充足，可以满足厂商的需求.

4 结语

本文以芯片规格测量系统为例，将多元测量系统分析方法应用到机器视觉领域中，考虑了芯片长度和宽度的相关性，避免了相关部分重复计算的问题，更精确地对测量系统进行能力评价.同时，使用一对总体指标（%P/Tm和%R&Rm），代替一元分析的多组测量指标，有利于对多元测量系统进行整体能力评价.

此外，传统的测量系分析大多以零件和操作者为波动源，但芯片规格机器视觉系统自动化程度很高，测量过程中人员的波动可以忽略.而CCD相机、光源、显微镜等设备的使用，又使芯片位置、放置角度等成了新的波动源，形成一个多因子设计.本文将这些因子充分地考虑到试验设计当中，基于对波动源的准确估计，给出测量系统是否合乎要求的明确判断.随着科技的发展，越来越多的新式测量系统被应用的生产实践中，我们在对其进行测量系统分析时，要充分考虑每个操作系统的特殊性，具体问题具体分析，准确识别波动源，不能局限于传统模型.

本文的不足之处在于，随着波动源的增多，交叉模型实验次数剧增，比较耗费时间与人力成本.因此，多因子测量系统分析如何减少试验次数，是一个值得继续探讨的问题.

[1]MEGAHED F M，WOODALL W H，CAMELIO J A.A review and perspective on control charting with image data[J].Journal of Quality Technology，2011，43（2）：83-98.

[2]HUANG K Y.Detection and classification of areca nuts with machine vision[J].Computers&Mathematics with Applications，2012，64（5）：739-746.

[3]王宝锋，齐志权，马国成，等.一种基于雷达和机器视觉信息融合的车辆识别方法[J].汽车工程，2015，37（6）：674-678.

[4]贺继林，郑海华，赵喻明，等.基于视觉的探测机器人导航[J].华中科技大学学报：自然科学版，2013，41（S1）：267-270.

[5]KACHITVICHYANUKUL V，LUONG H T，PITAKASO R. Color-based image analysis for statistical sausage production control[C]//Proceedings of the Asia Pacific Industrial Engineering&Management Systems Conference.Cheju，Korea：Korean Institute of Industrial Engineers（KIIE），2012：45-48.

[6]MAJESKE K D.Approving vision-based measurement systems in the presence of within-part variation[J].Quality Engineering，2012，24（1）：49-59.

[7]马琳，何桢.六西格玛管理 [M].北京：中国人民大学出版社，2007.

[8]BURDICK R K，BORROR C M，MONTGOMERY D C.A review of methods for measurement systems capability analysis[J]. Journal of Quality Technology，2003，35（4）：342-354.

[9]MONTGOMERY D C.Introduction to Statistical Quality Control[M].New York：John Wiley&Sons，2007.

[10]WOODALL W H，BORROR C M.Some relationships between gage R&criteria[J].Quality and Reliability Engineering International.2008，24：99-106.

[11]SWEENEY S.Analysis of two-dimensional gage repeatability and reproducibility[J].Quality Engineering，2007，19（1）：29-37.

[12]VOELKEL J G.Gauge R&R analysis for two-dimensional data withcirculartolerances[J].JournalofQualityTechnology，2003，35（2）：153-167.

[13]MAJESKE Karl D.Approval criteria for multivariate measurement system[J].Journal of Quality Technology，2008，40（2）：140-153.

[14]吴小芳，何桢，施亮星.基于向量的多元测量系统能力评价指数[J].系统工程，2013，31（3）：123-126.

[15]马逢时，周暐，刘传冰.六西格玛管理统计指南：MINITAB使用指导[M].2版.北京：中国人民大学出版社，2007：384.

Application of multivariate measurement system in machine vision

SHI Liang-xing，REN Hai-jia，XIAO Hang
（College of Management and Economics，Tianjin University，Tianjin 300072，China）

Univariate measurement system analysis may not assess the multivariate systems accurately.To address this issue，influential factors in the machine vision system is explored and a new sources of variation model for the measured values is established.Crossed design and multivariate analysis of variance （MANOVA）method are used to estimate the covariance matrices，which are the inputs for multivariate reproducibility and repeatability. The aforementioned method is applied in a chip size machine vision system and good results are achieved.

multivariate measurement system；machine vision；repeatability；reproducibility

TB9；TP391.41；F406.3

A

1671-024X（2015）05-0067-04

10.3969/j.issn.1671-024x.2015.05.014

2015-07-03

国家自然科学基金资助项目（71102140）

施亮星（1977—），男，博士，副教授，主要研究方向为质量管理、六西格玛管理、工业工程.E-mail：shi@tju.edu.cn