测量船变形误差对轨道精度的影响分析*
倪 兴 茅永兴 薛国虎 戴正旭 陈红英
(中国卫星海上测控部 江阴 214431)
测量船变形误差对轨道精度的影响分析*
倪 兴 茅永兴 薛国虎 戴正旭 陈红英
(中国卫星海上测控部 江阴 214431)
航天测量船执行测控任务时是在海上进行的,受风、浪、涌的影响,船体会产生扭曲变形,外测数据受变形的影响,必须修正后才能使用,变形误差对外测数据、定轨精度都有影响。为了分析变形误差对轨道精度的影响,进行了仿真试算,以任务中实际测量的变形角作为真实值,对其添加一定的误差后进行仿真,比较分别利用实测数据和仿真数据进行处理后的定轨结果,考察变形误差对轨道精度的影响。结果表明:变形误差是测量船的一项重要误差,其对地球同步卫星初轨的影响是百米级的,不可忽视,提高变形测量的精度,便能提高定轨的精度。
航天测量船; 变形; 误差; 轨道
Class Number V557
1 引言
远望号航天测量船在海上动态条件下对飞行器进行跟踪测量,是我国航天测控网不可或缺的重要组成部分,船载外测设备采用单站定位体制,其测轨数据对轨道确定起到了很重要的作用。测控设备在航天测量船上是沿船艏艉线分散布局的,设备之间存在着一定的距离,由于船体并不是一个刚体,在受到摇摆、风浪、海流等各种因素的作用时,船体姿态随时在变化,船体各部分也会产生扭曲变形,使得测量设备坐标系与惯导坐标系的对应轴不平行,从而导致变形量将直接影响船载外测设备的测角精度。所以,航天测量船上的外测设备,都要在其基座与惯导基座之间建立船体变形测量,并在数据处理时,进行变形量的修正[1~2]。因此变形测量的精度对外测数据、轨道确定的精度都有影响,变形测量误差影响理论上的分析已经比较完善了,但对各类轨道的具体影响未有数据上的支持,为此建立数学模型,进行了仿真试算。
2 船体变形测量简介
航天测量船基准坐标系的原点定义在惯导中心平台,测控设备沿船艏艉线分布,测控设备的基座与基准坐标系的原点有一段距离,测控设备坐标系与基准坐标系也不平行,因此,测控设备坐标系与基准坐标系的转换有三个平移量和三个旋转量。实际工作中,将三个平移量(即测控设备坐标系的原点在基准坐标系中的坐标)看作常量,对三个旋转量进行测量,即是船体扭曲引起的变形量。
航天测量船船体变形量以三个角度量来描述,参见示意图1。船艏艉绕节线的相对转角ψb为纵挠角,船艏艉绕艏艉线的相对转角θb为横扭角,船艏艉绕甲板垂线的相对转角Kb为艏挠角。变形测量为光电测量,其基本原理是:在需要测量相对变形量的两个设备基座上,一个基座上安装一个发射光管,发出一束平行光,在另一个基座上安装一个接收光管,接收发射管发出的平行光束。接收光管像面上装有光电转换器件线阵CCD,落在CCD上光斑的位移量即代表变形量,因此,船体变形测量设备是一种精密的光学测角装置[3~4]。

图1 船体变形定义示意图
由测量船船体变形角定义可知,变形测量是测两个设备基座间的船体变形量,而变形修正必须得到两个直角坐标间的相对角旋转量,这就要建立变形测量参数与两坐标间相对角旋转量的关系。船体变形测量问题,可以看做刚体绕固定点的转动,确定绕固定点转动的刚体的位置,一般采用欧拉角的方法。所以只要得到船体变形角Kb、ψb、θb与欧拉角Kb′、ψb′、θb′的关系,便可以进行变形修正。取刚体赖以转动的定点O为原点,通过O作固定坐标系O-xb1yb1zb1和与刚体固连的动坐标系O-xb2yb2zb2,进行三个独立的转动,得到三个转动角Kb′、ψb′、θb′,即为欧拉角,用它们可确定刚体相对固定坐标系O-xb1yb1zb1的位置,见图2[5]。

图2 欧拉角示意图
经过计算,可得欧拉角与变形角的关系为
(1)

3 船体变形误差对轨道的影响
对陆站来说,其误差主要是站址误差和设备测量误差,而陆站的站址可以通过精确的大地测量获得,误差很小,因此陆站的主要误差便是设备测量误差。而航天测量船系统的测量数据要比陆站复杂,误差源也更多。首先航天测量船在海上是运动的,其位置的测量误差会影响到总误差,而受风、浪、涌的影响产生的船摇、变形,其测量误差同样会影响总误差,再加上设备本身的测量误差,因此,测量船的误差是测控设备、船摇、变形、船位误差的合成,即[9]
(2)
式中:σP为总误差,σPl为雷达位置误差,σPy为船摇位置误差,σPb为变形位置误差,σPw为船位位置误差。
若只考虑变形误差,有
(3)
变形误差可以等效成测量设备的方位和俯仰角误差。如果存在船体变形误差ΔK,Δψ,Δθ,产生的测量设备方位和俯仰角等效误差为[10]
(4)
于是有
(5)
假设纵挠与横扭是等精度测量的,即σψ=σθ,则由变形引起的目标位置误差为
(6)
当只考虑变形误差时,此即为船载外测设备的定位精度,从式(6)可以看出,误差只与距离和仰角有关,且误差随距离的增大而变大。
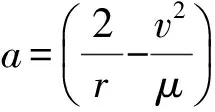
(7)
变形对速度的影响很小,可以忽略,于是有
(8)
将σr代入即得变形误差对轨道半长轴的影响。
4 仿真计算
以航天测量船参加地球同步卫星轨道入轨段任务中变形系统测得的变形角作为真实值,对航挠、纵挠、横扭分别添加符合其精度指标的随机误差后进行仿真,再分别利用真实变形角和仿真变形角进行数据处理并定初轨,对定轨结果进行比较,考察变形测量随机误差对初轨的影响。
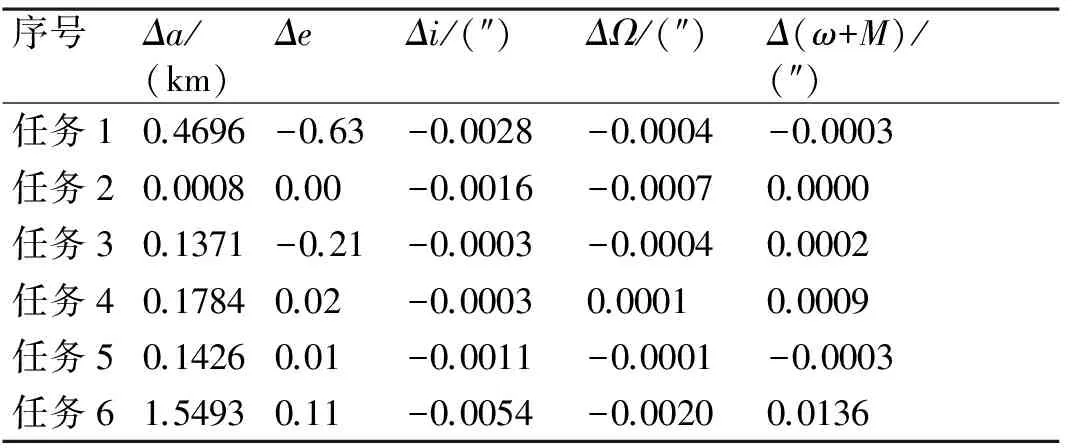
表1 航挠误差对轨道的影响
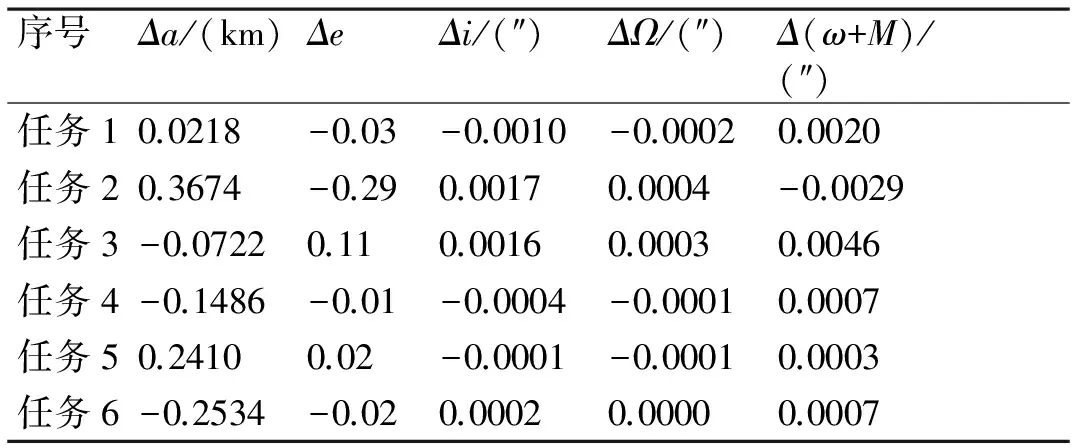
表2 纵挠误差对轨道的影响
从计算结果可以看出,变形误差对初轨半长轴的影响从0.8m~1.5493km,数量级基本是百米级的,对轨道的结果影响不可忽视。

表3 横扭误差对轨道的影响
5 结语
以往对航天测量船变形误差进行分析的过程都是从理论上进行,未有量级上的分析。本文通过仿真计算,明确了变形误差对同步卫星入轨段轨道半长轴影响的量级基本是百米级的,少数情况下可达米级和千米级。为简化分析,只考虑了单项误差的影响,未分析误差耦合效应对轨道的影响,下一步要做的工作是分析误差耦合的影响,以及变形误差对其它各类轨道的影响。
[1] 张忠华,李晓勇,杨磊,等.航天测量船船姿数据处理方法[M].北京:国防工业出版社,2009.
[2] 江文达.航天测量船[M].北京:国防工业出版社,2002.
[3] 简仕龙,费加兵,刘冰,等.航天测量船海上测控技术概论[M].北京:国防工业出版社,2009.
[4] 李辉芬,张忠华,朱伟康,等.航天测量船变形修正方法与使用策略研究[J].飞行器测控学报,2010,29(3):43-47.
[5] 李晓勇,张忠华,朱伟康,等.航天测量船船体变形数据的处理[J].光学精密工程,2009,17(2):445-452.
[6] 李晓勇,张忠华,何晶.船体变形对航天测量船外弹道测量的影响[J].飞行器测控学报,2006,25(3):7-12.
[7] 王建军,王颖.光栅法在船体横扭角测量中的应用[J].光学精密工程,2003,13(3):371-375.
[8] 李向荣,乔彦峰,刘微,等.船体三维角度变形的自准直干涉测量方法[J].光电技术,2005,31(5):761-763.
[9] 倪兴,李晓勇,薛国虎,等.测量船姿态误差影响分析[J].四川兵工学报,2014,35(5):149-151.
[10] 潘良,刘新明,王珏,等.航天测量船船姿船位测量技术[M].北京:国防工业出版社,2009.
Analysis on Precision of Orbit about Influence of Hull Deformation Error for TT&C Ship
NI Xing MAO Yongxing XUE Guohu DAI Zhengxu CHEN Hongying
(China Satellite Maritime Tracking and Controling Department, Jiangyin 214431)
Space-tracking ships must face various complicated job-enviroment when carrying out a traking task. Compared with a TT&C equipment on land, the error sources are more complex from equipments on ship, and the ge-sture error plays an important role in these sources. The hull deformation angel from the actual measurement is taken as a true value. After adding a fixed error to it, an simulation is carried on to compare the orbit results based on the true and simulated data. How the hull deformation error influences the orbit results is discussed to find that hull deformation error is an important error. Accuracy of the orbit measurement can be increased by controling the uncertainty of hull deformation.
TT&C ship, hull deformation, error, orbit
2015年6月3日,
2015年7月23日
倪兴,男,硕士,工程师,研究方向:外测数据处理。茅永兴,男,硕士,研究员,研究方向:航天测控总体。薛国虎,男,硕士,高级工程师,研究方向:航天测控总体。戴正旭,男,工程师,研究方向:外测数据处理。陈红英,女,工程师,研究方向:数据处理与精度分析。
V557
10.3969/j.issn.1672-9730.2015.12.043

