潜射战术导弹水弹道测量中的算法应用研究*

单玉浩 施建礼 彭文辉

(海军潜艇学院 青岛 266041)



潜射战术导弹水弹道测量中的算法应用研究*

单玉浩 施建礼 彭文辉

(海军潜艇学院 青岛 266041)

现有潜射战术导弹射击训练中,对于导弹弹道的监控只有出水之后的空中弹道,而水中段尚无有效的监测手段。而在训练打靶过程中,水中段是最薄弱环节,导弹最易出现故障且故障原因难以确定,水弹道测量将为这些问题的解决提供依据。论文将MEMS惯性传感器应用于潜射战术导弹水弹道测量中,以捷联惯导姿态更新中最恶劣的工作环境——锥运动作为仿真环境,分析四阶龙格库塔法和毕卡算法的优劣,并以梯形公式计算毕卡算法中的角增量,仿真得出的结论有很好的工程实用价值。

潜射武器; 捷联算法; 毕卡算法; 四阶龙格库塔算法

Class Number TJ630.33

1 引言

随着现代战争的需要,高精度制导武器迅速发展起来,潜射战术导弹作为潜艇的主战武器,其射程已达到几百甚至上千公里,因此要求其具有相当高的制导精度。惯导技术从产生到发展,已广泛应用到军事领域,其不受外界环境的限制,不需要接收外界数据,可靠性高。而且随着静电陀螺、光纤陀螺等高精度陀螺的产生,惯导系统正朝着小型化、高精度的方向发展[1]。

潜射战术导弹打靶监控手段较多,诸如差分GPS技术、靶场光电经纬仪交会测量技术,但是这只是针对导弹出水后空中段弹道的测量,对于其在水中段的监控目前尚未形成有效手段,考虑导弹内部空间小,水下段时间短的问题,传统的GPS等手段已不能满足测量需求,本文考虑将捷联式惯导系统应用于潜射战术导弹水弹道测量上。捷联式惯导系统以数学平台代替物理平台,其体积小、质量轻、易于安装,因此广泛应用于潜射战术导弹上。这类惯导系统虽然略去了复杂的物理平台,但其相应的算法就变得相当复杂,优化捷联算法可以保证数学平台的求解精度和快速性。捷联惯导中陀螺输出的解算是整个系统运动参数解算的基础[2],其精度决定了整个系统的精度,因此研究系统的姿态解算算法可以很大程度提高整个武器系统的反应能力和精度。

MEMS技术应用在惯性技术上就产生了各种MEMS惯性传感器,其中比较突出的体现就是硅微加速度计和硅微陀螺,这种惯性器件体积小、质量轻、成本低、可靠性高、易于安装[3],被广泛应用到民航及战术导弹领域。潜射战术导弹水下发射时间短,因此要求运动参数解算速度足够快且惯导系统体积质量足够小,不会影响导弹的力学环境和其他设备的正常工作,因此选用MEMS惯性测量组件作为水弹道测量元件。

2 姿态解算算法

武器系统制导精度不仅取决于惯导系统的硬件精度,而且很大程度上更取决于算法的精度。姿态阵的计算是捷联算法中最重要的部分[4],捷联式惯导系统的姿态解算算法主要包括方向余弦法、欧拉法、四元数法和旋转矢量法,其中四元数法算法简单,计算量比较小,易于实现,因此在工程上较为实用。

2.1 四元数微分方程

表征地理坐标系至载体坐标系的旋转四元数微分方程可表示为[5]

(1)

其中

2.2 定时采样的毕卡算法

毕卡算法是通过角增量来计算四元数的一种算法,但MEMS陀螺的输出一般为角速度信息,因此必须用合适的方法将角速度转换为角增量。

采用定时采样法,采样时间间隔一定,tk+1时刻旋转四元数的解为[1]

(2)

其中

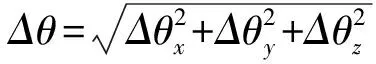
在实际计算中,由于指数形式和三角运算的计算复杂,因此为减少运算的复杂程度,对eA进行泰勒级数展开:

(3)

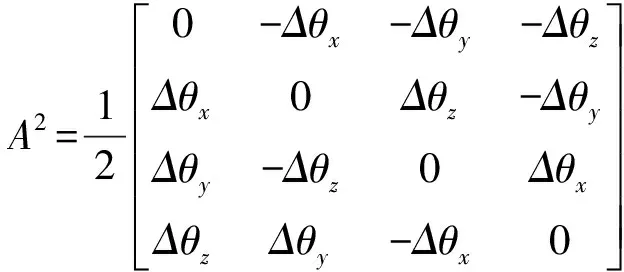
所以

代入式(3)可得四元数的各阶近似算法。

一阶近似算法为

Q(tk+1)=(I+A)Q(tk)

二阶近似算法为

三阶近似算法为

四阶近似算法为

角速度与角度之间存在如下关系:

(4)

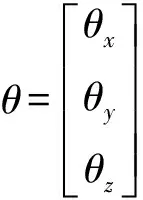
由上式可得角增量的近似值为

Δθ(tk)=h·ω(tk)

(5)

其中h为更新周期,h=tk+1-tk。通过各时刻的角速度信息的输出,利用欧拉式(5)即可得到各时刻的角增量信息。

通过角速度得到角增量也可以通过数值积分来完成,对微分方程(4)两端在区间[tk,tk+1]上积分,得

(6)

若用梯形公式计算式(6)右端,即

Δθ(tk) =Δθ(tk+1)-Δθ(tk)

(7)

2.3 四阶龙格库塔算法

假设姿态更新时间间隔为h,用四阶龙格库塔法解式(1),得递推形式为

(8)

四元数与坐标变换矩阵及姿态角的关系可表示为[6]

通过求解四元数微分方程,可以不断得到姿态四元数,进而可以确定姿态矩阵,结合真值表就可以计算出航向角、俯仰角和横滚角的真实值[7～8]。

3 圆锥运动下算法的可靠性验证

对捷联陀螺来说,圆锥运动是最恶劣的工作环境,它会引起数学平台的严重漂移[9],因此,如果能保证在圆锥运动条件下算法的可靠性,那么其他环境下算法也是可靠的。

在实现过程中,将圆锥运动的姿态四元数的解析表达式作为真值,分别检验采用梯形公式的四阶毕卡算法和四阶龙格库塔法的精度。

1) 仿真条件取圆锥运动的半锥角为a=1*pi/180;旋转角速度为w=pi/3(rad/s),姿态更新周期为h=0.01s

当转轴在yoz平面时,地理坐标系至载体坐标系的旋转四元数为

角速度为

得到两种算法的姿态角误差分别如图1～图6所示。

图1 毕卡算法的横滚角误差

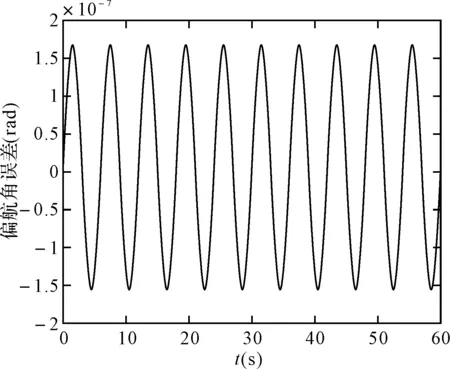
图2 毕卡算法的偏航角误差

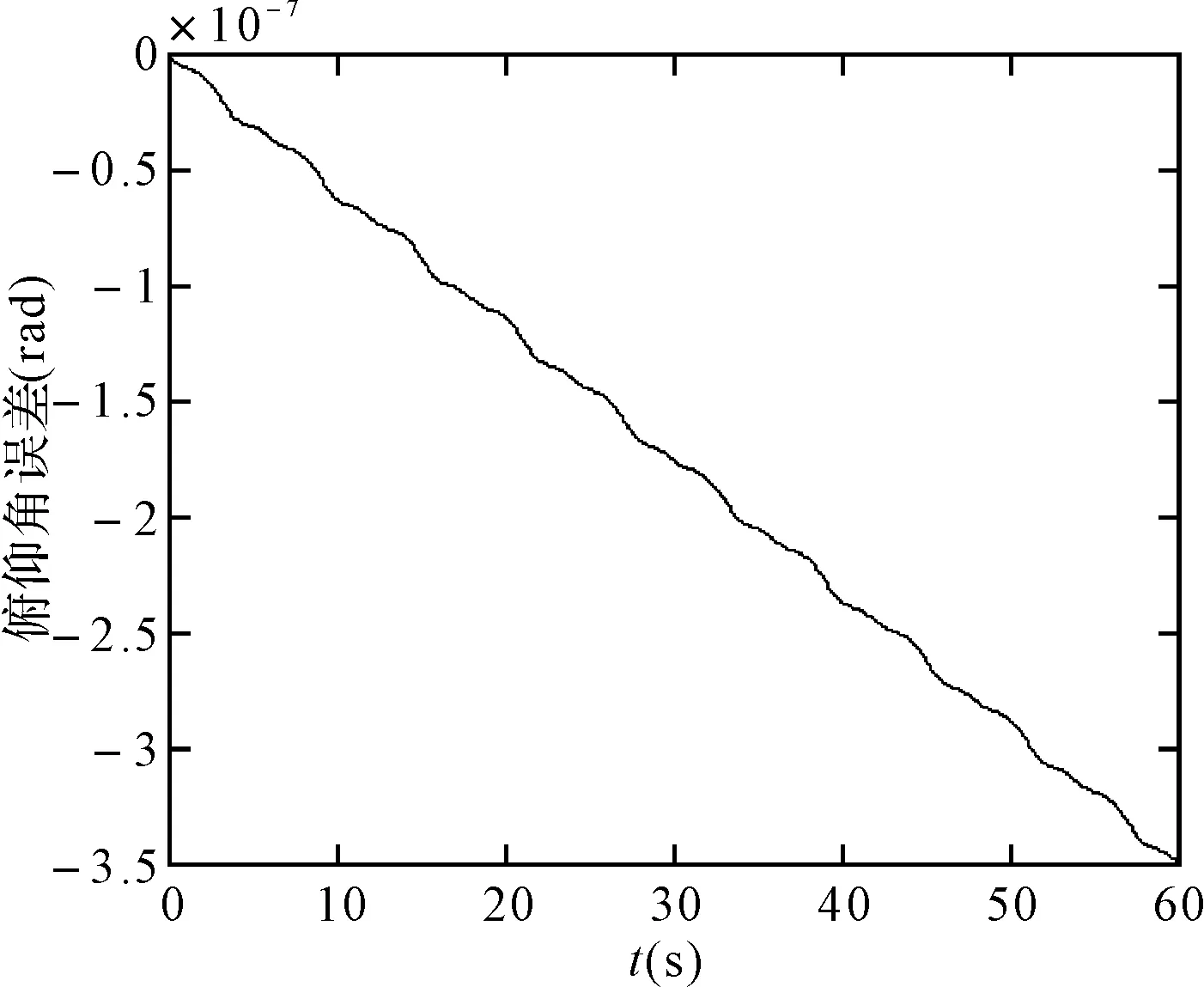
图3 毕卡算法的俯仰角误差

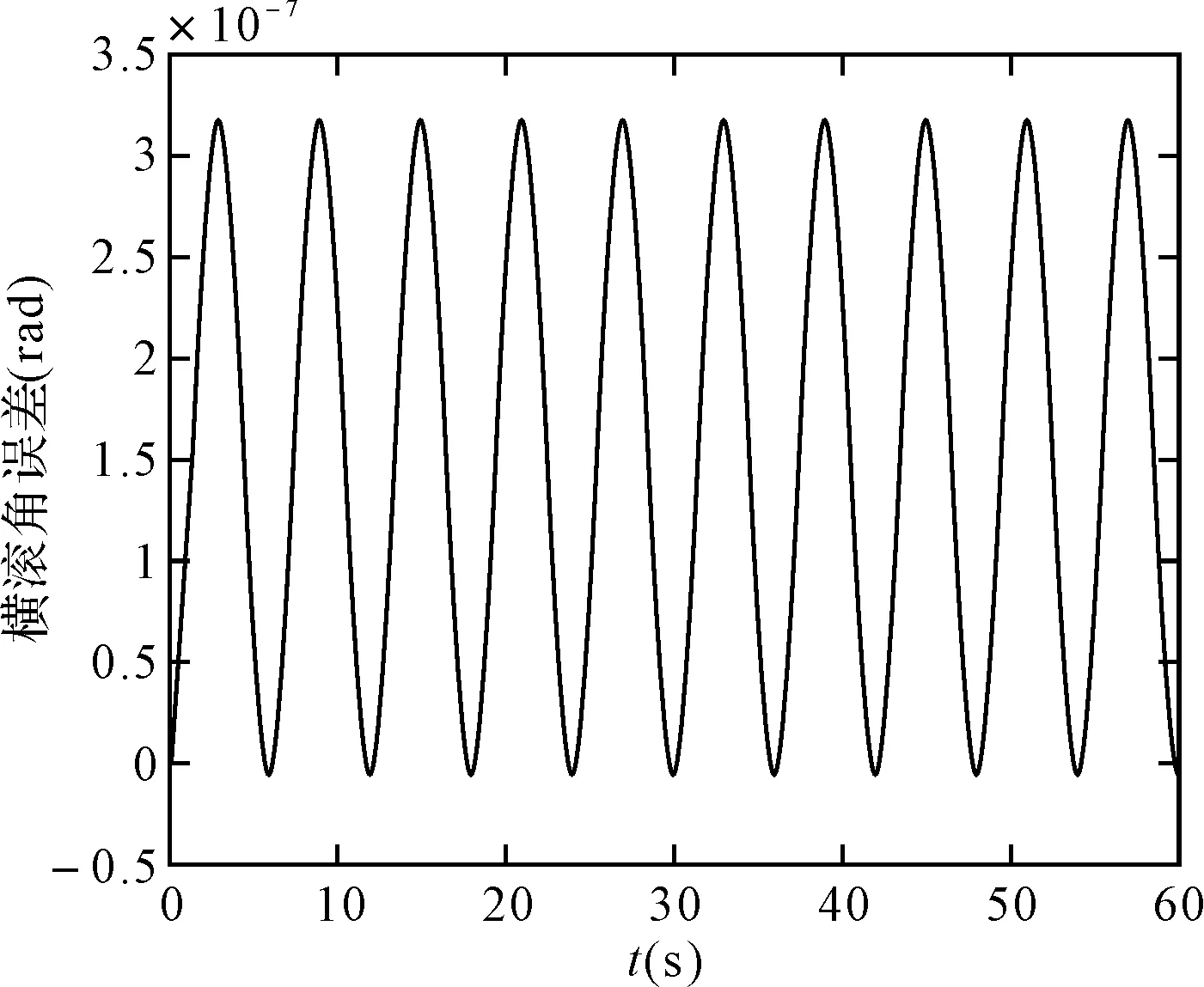
图4 龙格库塔法的横滚角误差

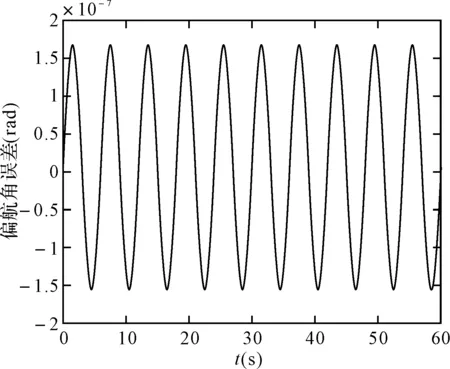
图5 龙格库塔法的偏航角误差

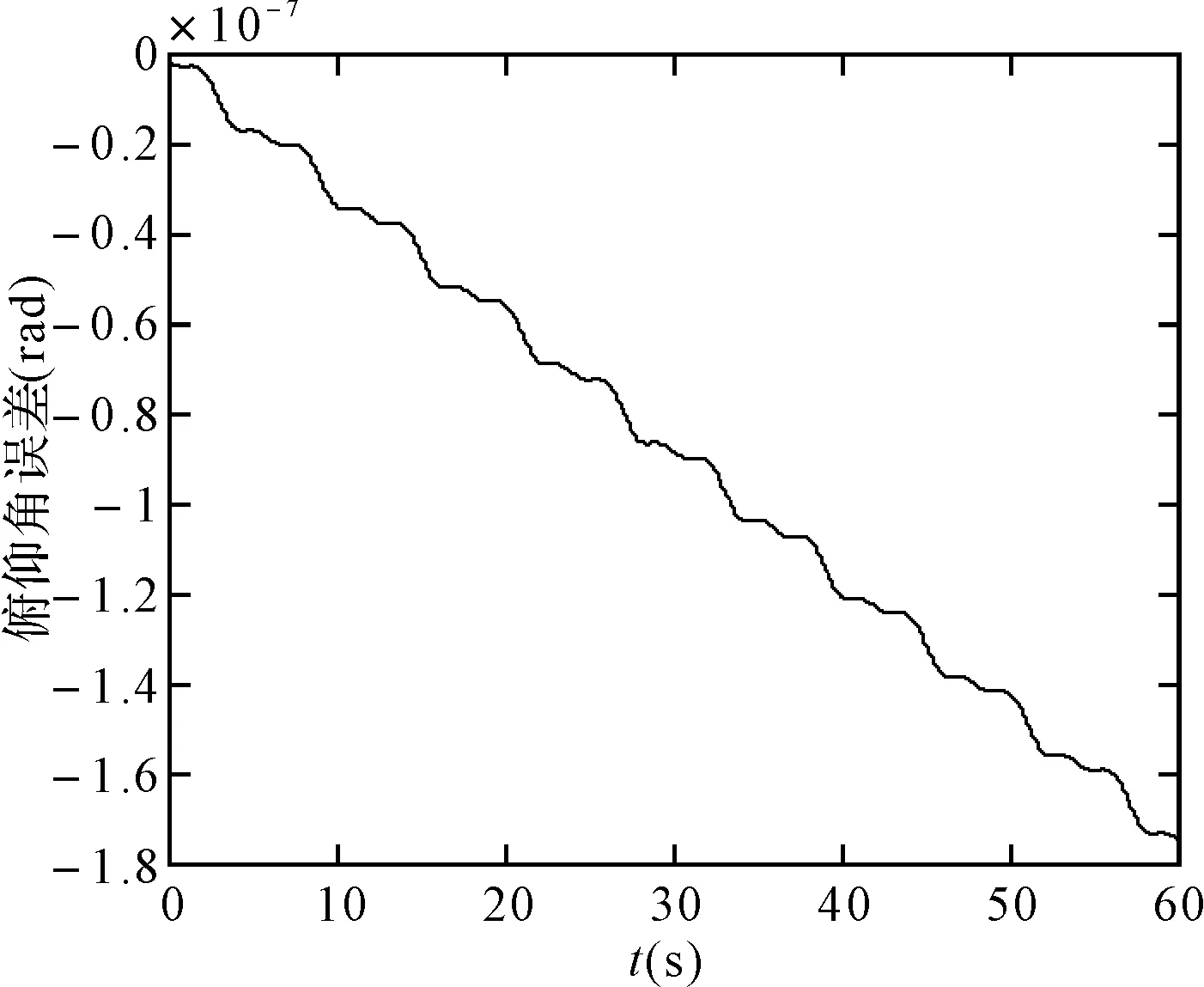
图6 龙格库塔法的俯仰角误差

当转轴在xoy平面上的圆锥运动,地理坐标系至载体坐标系的旋转四元数为

角速度为

得到两种算法的姿态角误差分别如图7～图12所示。

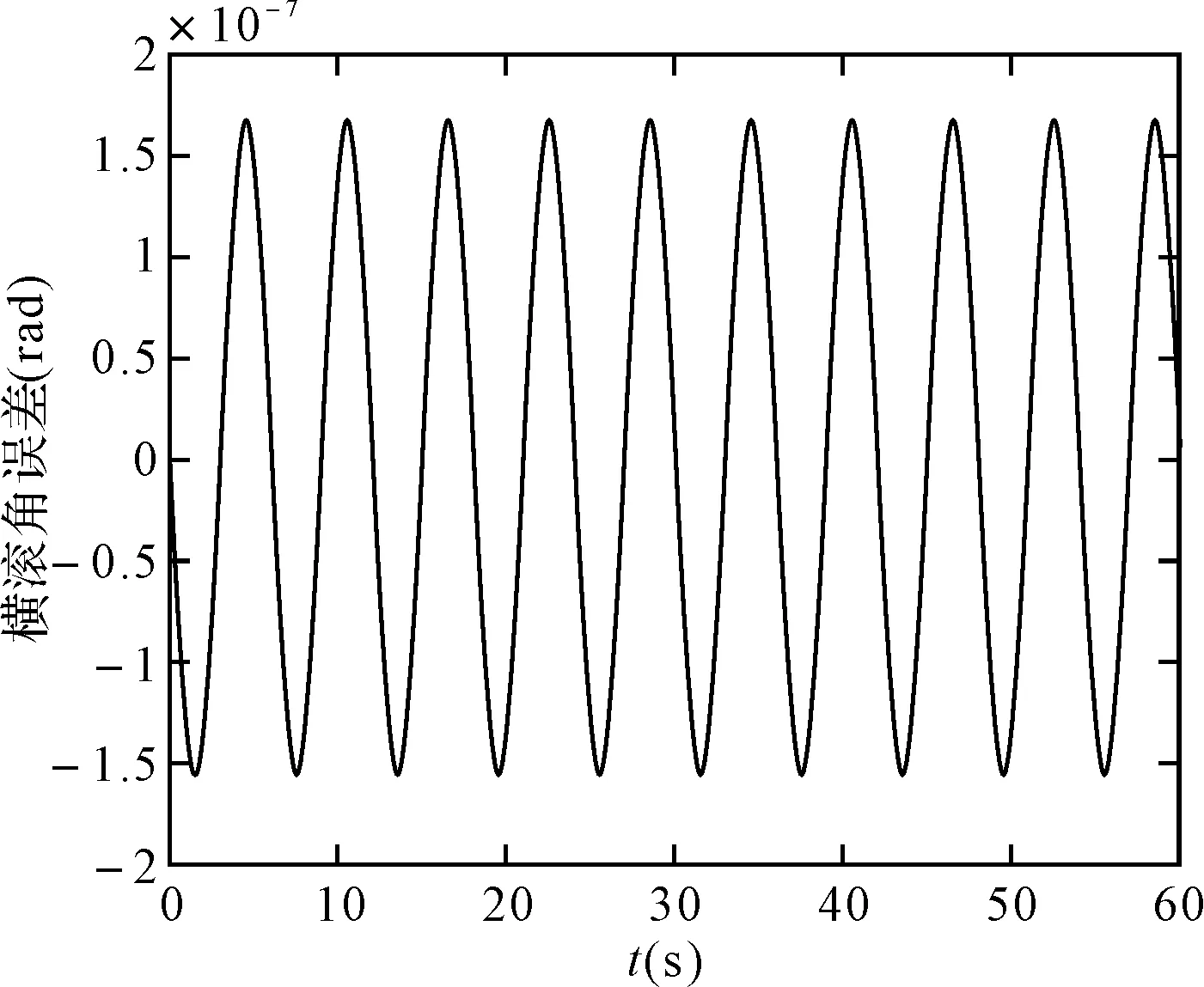
图7 毕卡算法的横滚角误差

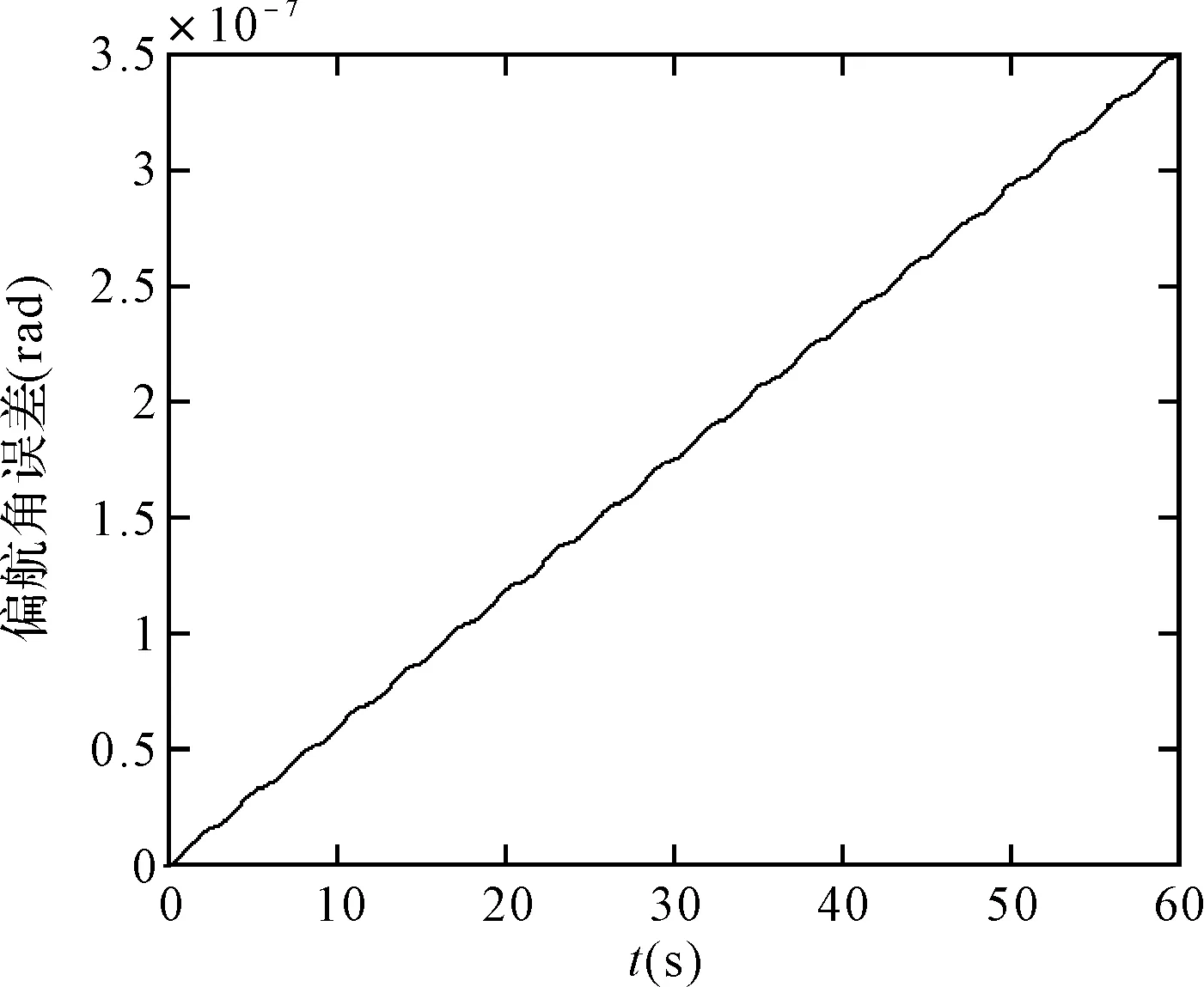
图8 毕卡算法的偏航角误差

图9 毕卡算法的俯仰角误差

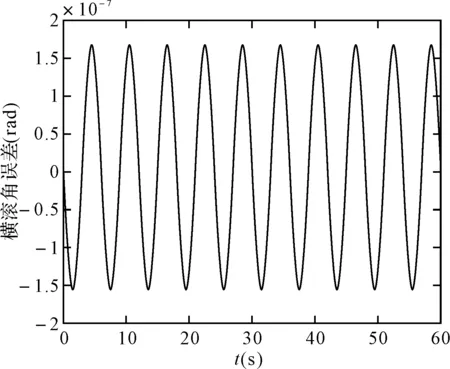
图10 四阶龙格库塔算法的横滚角误差

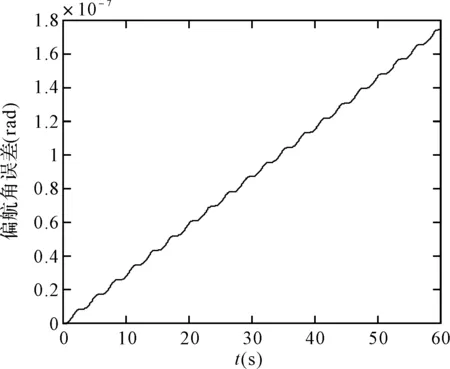
图11 四阶龙格库塔算法的横滚角误差

图12 四阶龙格库塔算法的横滚角误差

当转轴在xoz平面上,地理坐标系至载体坐标系的旋转四元数为

角速度为

得到两种算法的姿态角误差分别如图13～图18所示。

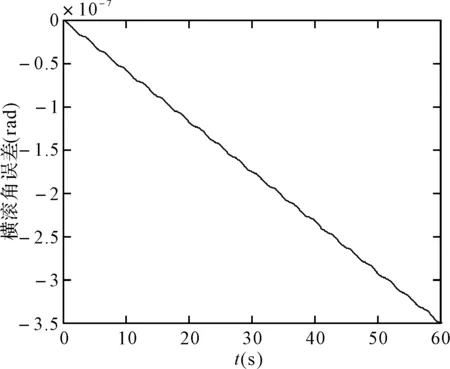
图13 毕卡算法的横滚角误差

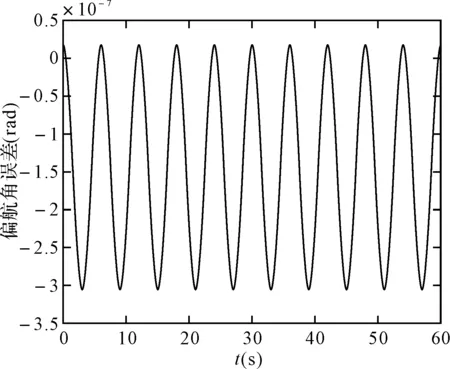
图14 毕卡算法的偏航角误差

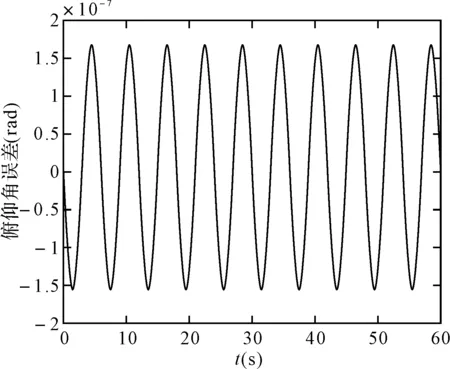
图15 毕卡算法的俯仰角误差

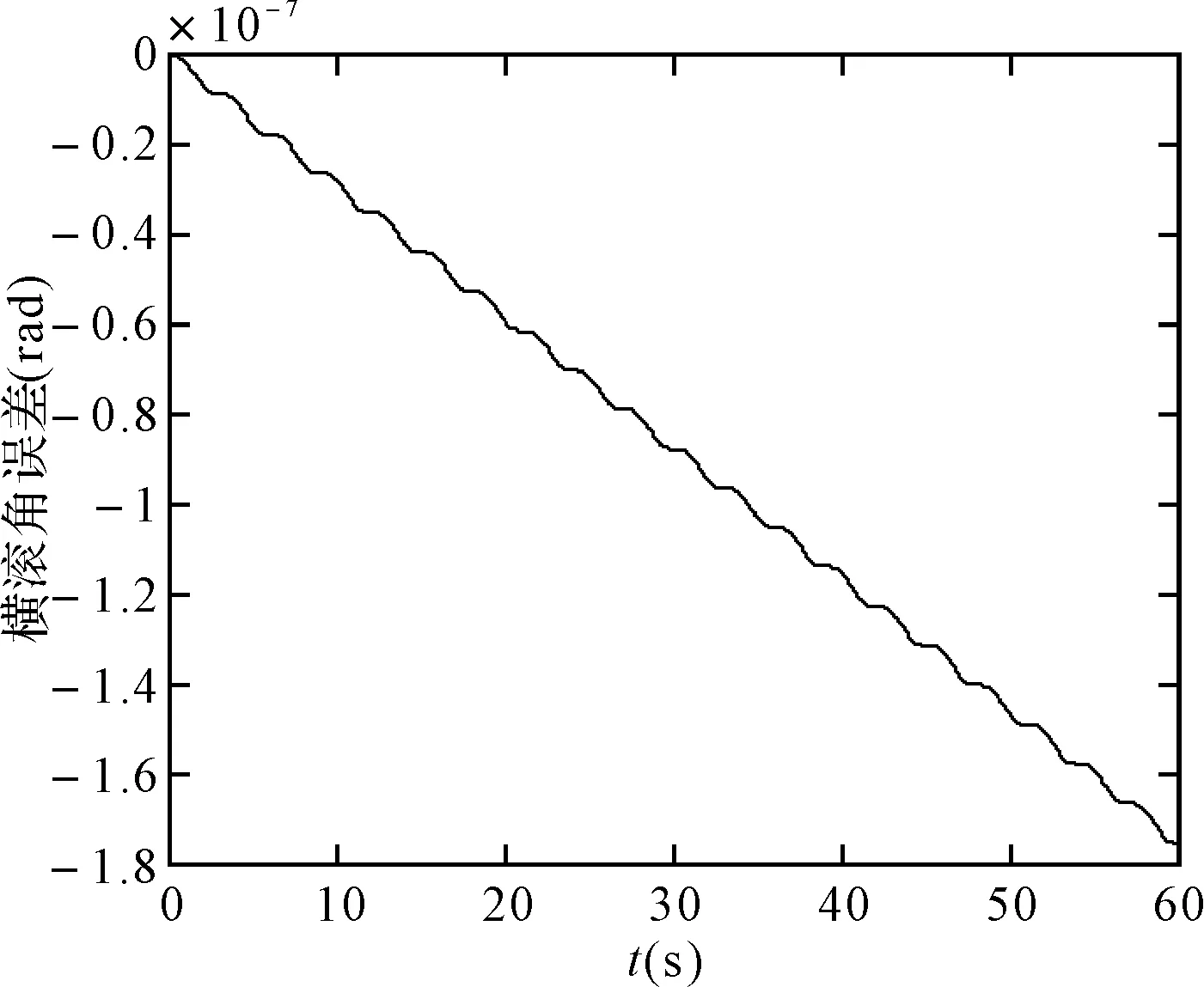
图16 四阶龙格库塔法的横滚角误差

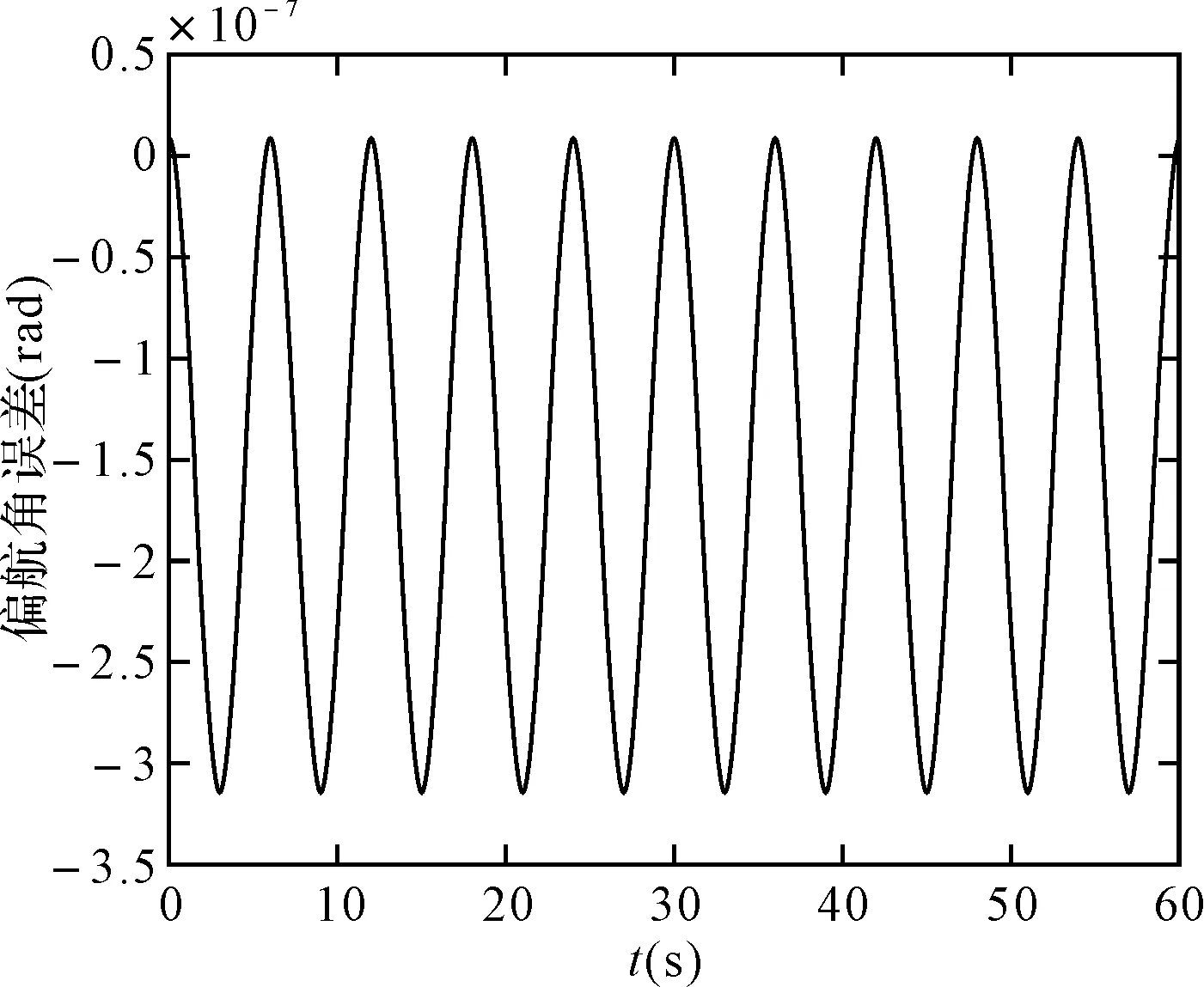
图17 四阶龙格库塔法的偏航角误差

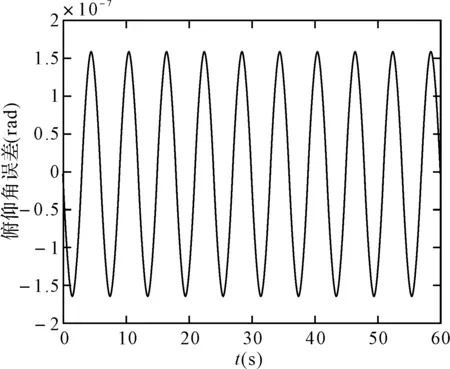
图18 四阶龙格库塔法的俯仰角误差

可以看出,在取角速度为w=pi/3(rad/s),姿态更新周期为0.01s时,60s内锥运动的龙格库塔法和毕卡算法的姿态计算误差都在10-7数量级上,针对锥运动的旋转轴不同可以看出,绕转轴的姿态角计算误差会逐渐发散,算法产生严重漂移,且毕卡算法的发散速度更快。

2) 上述条件仿真出的结果能满足精度要求,考虑增大圆锥运动的半锥角[10],转轴在yoz平面内,半锥角为a=20*pi/180时,旋转角速度为w=pi/3(rad/s),姿态更新周期为0.01s。

随着锥运动的半锥角的增大,两种算法的漂移也相应地增大,俯仰角的漂移最快,横滚角和偏航角的误差也逐渐发散,但龙格库塔法的算法漂移相对毕卡算法的速度较慢,在60s的时间内两种仿真精度在一个数量级上。

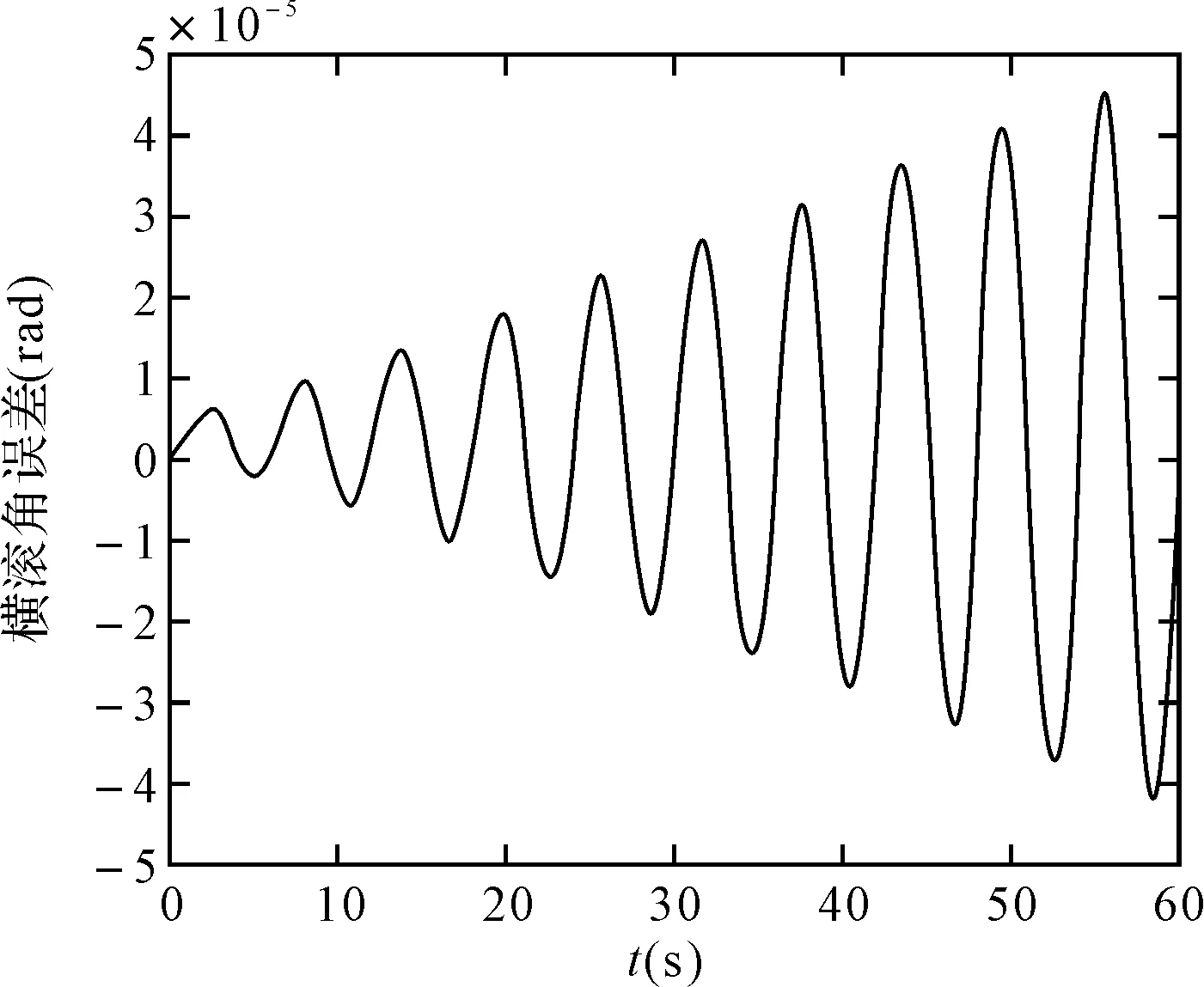
图19 毕卡算法的横滚角误差

图20 毕卡算法的偏航角误差

图21 毕卡算法的俯仰角误差

图22 龙格库塔法的横滚角误差

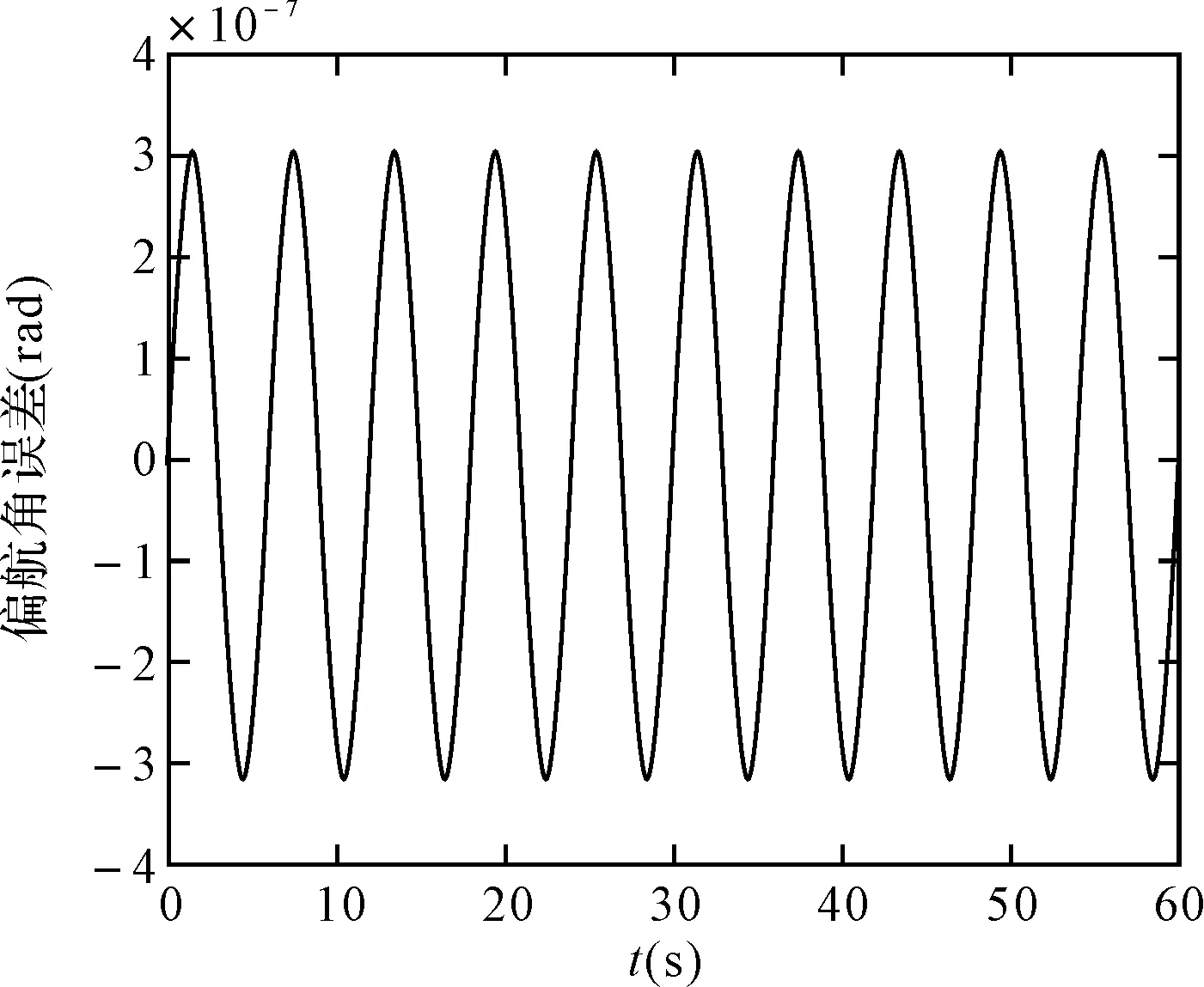
图23 龙格库塔法的偏航角误差

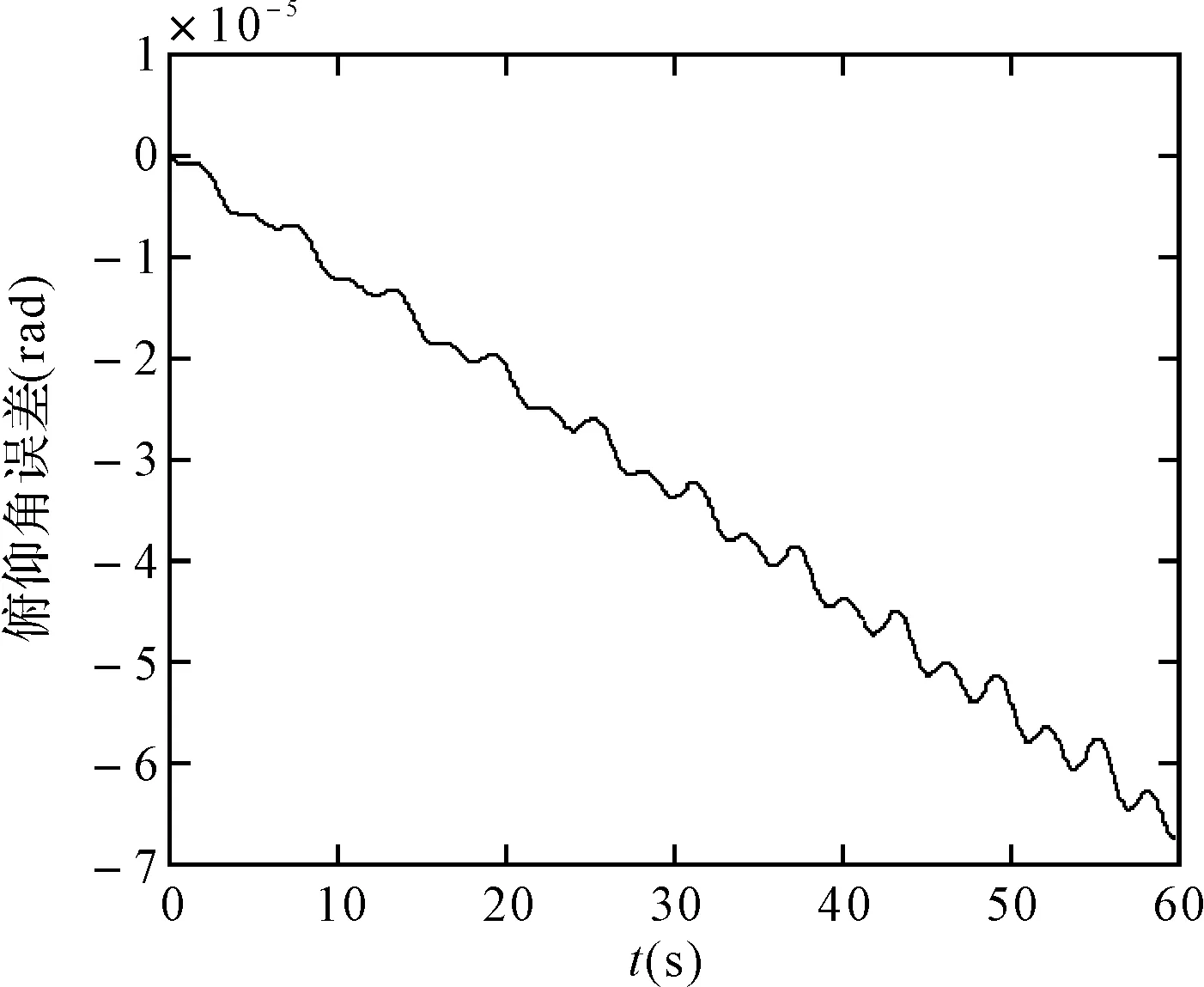
图24 龙格库塔法的俯仰角误差

4 结语

当振动比较小,运动较平稳时,四元数法中的毕卡算法和四阶龙格库塔法的精度相当,但随着振动加剧,环境条件更加恶劣时,四阶龙格库塔法精度要优于毕卡算法,算法漂移率较小,从运算精度上来讲,可选择四阶龙格库塔算法,但其在每步更新过程中需多次计算四元数微分方程式(1)右端的值,算法实现比较复杂,快速性和实时性略次于毕卡算法。Matlab仿真过程中使用tic、toc函数监测算法运行时间,四阶龙格库塔算法和毕卡算法的平均计算时间分别为1.0703e-04s和5.9295e-05s,毕卡算法的效率明显高于四阶龙格库塔算法,从运算速度上来讲,可选择毕卡算法。

对于潜射战术导弹来说,其水下发射环境恶劣,水下弹道时间短,对其弹道测量来讲,实时性和精度都是至关重要的,基于硬件系统考虑,在高采样率下要求同时进行捷联解算,这就需要算法相对简单,同时从本文的结论发现四元数法中的四阶龙格库塔法和毕卡算法的精度在同一数量级上,因此考虑使用毕卡算法作为姿态更新算法。由于捷联惯导器件直接固联在载体上,受载体的角振动影响大,引起误差发散很快,而且对于导弹这种高速运动体,振动环境恶劣,由高过载产生的非线性误差大且不易补偿,提高采样频率和姿态更新频率是保证解算精度行之有效的方法。

[1] 秦永元.惯性导航[M].北京:科学出版社,2006:1-4.

[2] 贺元军,卢晓东,吕春红.基于MEMS捷联惯导系统的解算与误差修正方法[J].计算机测量与控制,2010,18(6):1364-1366.

[3] 李荣冰,刘建业,曾庆华,等.基于MEMS技术的微型惯性导航系统的发展现状[J].中国惯性技术学报,2004,12(6):89-94.

[4] 孙丽,秦永元.捷联惯导系统姿态算法比较[J].中国惯性技术学报,2006,14(3):6-10.

[5] Qamar A, Shams, Michael Moniuszko, John C, Ingham. Applying MEMS technology to field[J]. Flight and Space Deployable Systems, IEEE,2001:246-255.

[6] 张荣辉,贾宏光,陈涛,等.基于四元数法的捷联式惯性导航系统的姿态解算[J].光学精密工程,2008,16(10):1964-1970.

[7] 杨淑洁.悬翼式微小飞行器姿态测量系统设计[D].哈尔滨:哈尔滨工业大学学位论文,2011:9-14.

[8] 赵鹏,沈庭芳,单宝堂.基于MEMS的微型无人机姿态仪的设计[J].太原:火力与指挥控制,2009,34(6):164-167.

[9] 季超,杨晓东.INS/GPS组合导航系统动基座初始对准研究[J].舰船电子工程,2012,32(55-57):164-167.

[10] Sameh Nassar, Klaus Peter Achwarz, Naserel Shemimy. Modeling Inertial Sensor Errors Using Autoregressive(AR) Models[J]. Navigation,2004,51(24):259-268.

Algorithm Application of Water Trajectory of Submarine-launched Missiles

SHAN Yuhao SHI Jianli PENG Wenhui

(Navy Submarine Academy, Qingdao 266041)

Aerial trajectory can be measured merely in the launch trainings of submarine-launched missiles, and underwater trajectory is not yet measured at present. Underwater trajectory is the most vulnerable in the whole trajectory and the breakdown reason is difficult to confirm. Measure of the underwater trajectory provides the possibility of breakdown analysis. The paper applies MEMS inertial sensors in underwater trajectory measurement, considering conical motion as attitude updating simulation environment. Trapezoid formula is used to calculate angle increment of Pirkanmaa algorithm, and analyse advantages and disadvantages of fourth order Ronge-Kutta method and Pirkanmaa algorithm. Ultimately conclusion by simulation is commendable to engineering application.

submarine-launched weapons, strapdown algorithm, Pirkanmaa algorithm, four order Ronge-Kutta

2015年3月1日,

2015年4月23日

单玉浩,男,硕士研究生,研究方向:图形图像处理。施建礼,男,副教授,硕士生导师,研究方向:维修与检测。彭文辉,男,讲师,研究方向:硬件设计与实现。

TJ630.33

10.3969/j.issn.1672-9730.2015.09.035