基于粗糙集的涡轴发动机型号发展综合评估决策模型*
章原发 蒋 涛 李荣辉
(1.海军指挥自动化工作站 北京 100036)(2.77126部队保障部 重庆 402260)
基于粗糙集的涡轴发动机型号发展综合评估决策模型*
章原发1蒋 涛2李荣辉1
(1.海军指挥自动化工作站 北京 100036)(2.77126部队保障部 重庆 402260)
根据新型号涡轴发动机质量要求,综合考虑系统设计与用户需求,以指标体系构建方法为指导,构建涡轴发动机型号发展评估指标体系。运用粗糙集理论对世界上典型的同类型涡轴发动机的各种指标进行数据挖掘,利用信息熵方法求出各指标的权重值,克服了传统主观赋权法的随意性与客观构权时可能存在的偏差。最后,建立涡轴发动机型号发展综合评价决策模型并用实例证明了这种方法的可行性。
涡轴发动机; 粗糙集; 综合评价; 指标体系; 信息熵
Class Number E917
1 引言
舰载直升机的发动机型号发展专业性强,技术含量高,投入资金多,涉及领域广,如何协调好各种因素的影响,使新型号的发动机既具有强大的功能又有高的可靠性、维修性、测试性是型号发展初期的重要工作之一。因此,建立一套科学、适用、综合的评价体系和有效的评价方法显得尤为重要。
目前对作战飞机、雷达、导弹、保障系统等的评价指标体系均已建立,但对发动机型号发展指标体系的研究却很少。随着舰载直升机需求的不断增加以及任务的不断复杂化,对涡轴发动机(本文特指舰载机的涡轴发动机)的要求也越来越高,要求发动机既能够提供强劲的动力又具有高的可靠性、安全性。Mavris D N[1]从任务能力(mission capability)、可用性(availability)、战时生存性(wartime survivability)、平时安全性(peacetime safety)及经济可承受性(affordability)等五个方面评价了作战飞机的总体设计。熊少华[2]从物质力、能动力、系统力三个方面构建了评价雷达情报网络作战能力的指标体系。朱斯高[3]从平均可成功发射导弹数、平均突防导弹数,平均命中导弹数三个方面构建了舰空导弹的评价指标体系。黄俊[4]从寿命周期费用、作战能力、可靠性、维修性、保障性、安全性、生存性、适应性等八个方面构建了作战飞机总体设计评价准则。刘大伟[5]从经济性、作战效能、研制风险三个方面构建了武装直升机的总体方案评价体系。可以看出,以上的指标体系都是针对不同的评价对象,基于不一样的评价目的建立起的,若直接用于涡轴发动机的型号发展评价,文献[1,4]虽然都考虑了很多影响因素,但大多数都可以归结为系统效能,对研制风险与研制周期的重视不够;文献[2~3]的专业针对性都太强,不适合用于涡轴发动机的型号评估;文献[5]虽然考虑研制风险的影响,但对于研制周期考虑仍有所欠缺。因此,在借鉴已有成果的基础上,结合涡轴发动机型号发展实际与我国军事工业的现状,综合考虑发动机型号发展的各方面因素,建立起适合发动机型号发展的综合评价指标体系,并利用粗糙集理论约简指标体系,挖掘世界上同类型的典型涡轴发动机各种指标数据,将指标权重问题转化为粗糙集的属性重要度问题,利用信息熵概念确定各指标的属性重要度,归一化后即为各指标权重,克服了传统主观赋权法的随意性与客观构权法可能存在的较大偏差。
2 涡轴发动机型号发展指标体系
2.1 指标体系的建立
指标体系是评价各待选方案的统一尺度,是建立决策模型与仿真实现的基础。因此,评价指标体系建立得是否科学、合理将直接影响到评价结果的可信度[5]。
涡轴发动机型号发展工程以用户的需求为中心,满足包括用户明示的、隐含的或者必须履行的一系列特性。型号发展的具体过程受国家科技水平、工业实力、财政能力等客观条件的制约,同时随着潜在对手在涡轴发动机领域的发展进步而不断变更发展目标。
根据涡轴发动机型号发展的评估目的,在寻求相关专家帮助的前提下,采用目标层次分析法与Delphi法组合分析的方法确定出涡轴发动机型号发展的评估指标集,运用粗糙集属性约简方法筛选出以系统效能、寿命周期费用、研制周期、研制风险四个指标作为综合评估的一级指标,并将各一级指标分解细化构成了最后的发动机型号发展评估指标体系,如图1所示。

图1 涡轴发动机型号发展评价指标体系
涡轴发动机型号发展的综合评估,考虑了型号发展中的各种影响因素,满足了全寿命综合评估的需要,各级指标根据其属性还可以细分。
2.2 指标介绍与计算
由于涡轴发动机一般都工作在潮湿、较腐蚀性等环境中,需要满足高轴功率与功重比的要求,同时要兼顾高可靠性、维修性、保障性、安全性等。因此,在涡轴发动机型号发展过程中不仅要使发动机具有较高的系统效能,同时还要在费用、研制风险、研制周期之间进行权衡。
1) 系统效能[6]。系统效能是系统在规定条件下完成规定任务的能力,是一种能力度量。系统完成任务的能力不仅与系统的固有性能参数有关,而且还与可靠性、维修性、保障性、安全性、生存性等有关。效能评估的方法很多,本文采用经典的效能评估模型,由美国工业界武器装备系统效能咨询委员会(WSEIAC)提出的ADC模型进行评估。
E=A×D×C
(1)
其中,E为涡轴发动机的系统效能;A为可用度向量,是涡轴发动机在执行任务开始时刻可用程度的度量,由可靠性、维修性、保障性几个部分构成;D为可信度矩阵,表示涡轴发动机在使用过程中完成规定功能的概率,由安全性、生存性、测试性几个部分构成;C是发动机系统完成任务的能力矩阵,表示系统在可用及可信条件下,能达到预定任务目标的概率,发动机完成任务的能力主要是由发动机的性能决定,包括轴功率、单位功率、功重比、耗油率、涡轮进气温度以及发动机的总体结构几个部分。
2) 寿命周期费用[7]。寿命周期费用是发动机系统从开始研究、设计、试制、批生产到部队使用维修保障等一系列费用的总和。是衡量发动机系统总费用与经济性的综合参数。根据涡轴发动机寿命周期的阶段划分,可以将寿命周期费用表示为
LCC=C1+C2+C3+C4
(2)
其中,C1为研究、设计与试制费,C2为生产费,C3为使用与维护保障费,C4为报废处理费。
3) 研制风险[8]。研制风险是指采办过程中在规定的费用、进度和技术约束下,不能实现发动机目标的可能性及所导致的一种度量。导致研制风险的因素很多,主要有技术风险、进度风险、费用风险、生产风险。因此,可将研制风险表示为
Pr=ksPs+ktPt+kcPc+kmPm
(ks+kt+kc+km=1)
(3)
其中,ks,kt,kc,km是进度风险Ps、技术风险Pt、费用风险Pc与制造风险Pm的权系数,这些系数需要根据实际的情况在专家的协助下完成。
4) 研制进度[9~10]。研制进度是指发动机型号发展完成论证阶段、方案选择阶段、工程研制阶段、设计定型阶段和生产定型阶段所用的时间。涡轴发动机研制进度的管理通常采用一些典型的项目进度管理方法,如关键路线法(CPM)、计划评审技术(PERT)、计划管理工作规划图(PMP)、网络评价技术(GERT)等。
3 基于粗糙集的综合评价决策模型
涡轴发动机型号发展的综合评价涉及指标众多,相互关系复杂,既有定性指标又有定量指标,既有统计数据的可量化指标,也有无统计数据或统计数据非常有限的指标,还有复杂非线性指标。传统的综合评估方法难于有效地对涡轴发动机型号发展评估指标体系进行决策分析,因此,采用能够有效处理不精确、不一致、不完备信息并最后能够得到客观权重的粗糙集方法对涡轴发动机的型号发展进行综合评估决策。建立基于粗糙集的综合评估决策模型分为以下几步:
1) 建立粗糙集模型信息系统。将系统效能、寿命周期费用、研制风险、研制周期等四项一级指标设为属性,则属性集为A={a1,a2,a3,a4},U={u1,u2,…,un}表示世界上同类型典型涡轴发动机的集合,ui={u1i,u2i,u3i,u4i}表示每个待选评价方案在这四项指标上的取值,即对象ui的一条信息。对象ui的属性值为aj(ui)=aji,(i=1,2,…,n;j=1,2,3,4),n表示对象个数。依此关系建立一个信息系统S=[U,A,V,f],其中,V是指标和评价结果的值集,f:U×A→V是信息函数,反映评价对象的各指标值与评价结果之间的对应关系。为了对各备选方案进行有效的综合评价,需要对指标进行标准化处理[11]。
2) 样本属性值离散化[12]。由于粗糙集方法只能处理离散化的数据,因此,在进行数据处理之前要先对样本属性值进行适当的离散化处理。通常采用的处理方法有专家离散法、等宽度区间法、等频率区间法、最小类熵法、Chimerge法、Senmi Naïve Scaler法、启发式离散算法等。在遵循简单性、精确性、易操作性原则前提下可以根据实际情况选择其中的一种或多种方法。
3) 指标权重确定[13~15]。样本属性值离散化后利用信息熵方法计算出每个指标的属性重要度,信息系统仍为S=〈U,A,V,f〉。设A′是属性集A的子集,即A′⊆A,则A′的信息熵

(4)
其中,等价关系IND(A′),A′⊆A构成U的一个划分,U/IND(A′)={X1,X2,…,Xm};P(Xr)=card(Xr)/card(U),r=1,2,…,m,m表示集合U在等价关系IND(A′)条件下的分类数量,card(Xi)表示集合Xi的“势”,当Xi为有限集合时,表示Xi所含元素个数。
利用粗糙集权重确定方法确定各个属性的重要度
SA(aj)=abs(H(A)-H(A-{aj}))
(5)
其中,abs(x)表示对x取绝对值,SA(aj)的值即是属性aj的重要度。
对式(5)归一化就得到了涡轴发动机型号发展综合评价体系中各一级指标的权重
(6)
4) 建立综合评价决策模型性。在以上工作的基础上可以建立起涡轴发动机型号发展综合评价决策模型
(7)

4 实例分析
某新型号舰载直升机的涡轴发动机共有三种待选方案,将这三种方案的各项指标进行线性标准化处理,即在专家的指导下与世界公认的第五代涡轴发动机的各项性能指标分为效益型与成本型两类进行比较,得出各待选方案的归一化值,如表1所示。
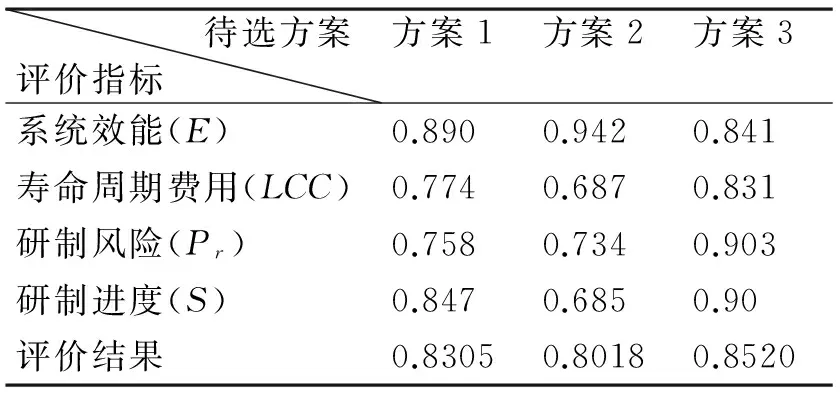
表1 新型涡轴发动机设计方案
收集归纳了世界上同类型的典型涡轴发动机(包括AH-64,UH-60,“超美洲豹”,“虎”式,SH-60B,卡-62R,AH-1G,贝尔212,RH-66,A129,“石茶隼”,“毛鼬”,“海王”,印度ALH,直-9,武直-10等直升机所用发动机,共12个型号)的各种原始数据,利用粗糙集方法、AHP法自底层指标原始数据计算出涡轴发动机型号发展的系统效能、寿命周期费用、研制风险、研制周期等四个第一级指标值。将计算出的各一级指标值进行指标归一化,结果如表2所示。
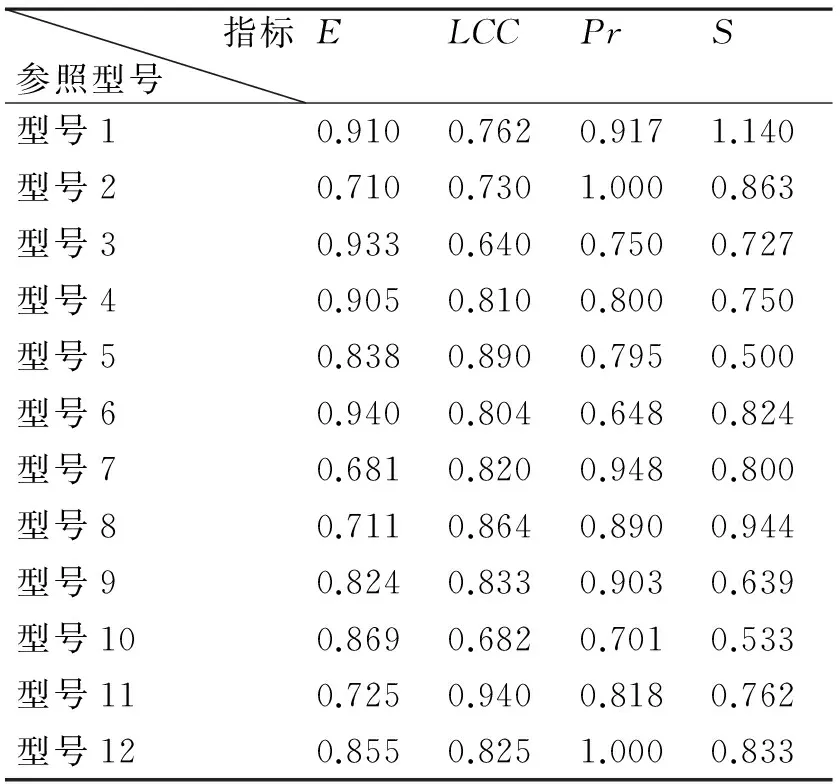
表2 世界同类型典型涡轴发动机指标
分析上面介绍的样本离散化方法后,根据涡轴发动机获得的原始数据情况,将表3中的数据运用启发式离散化算法对每个一级指标的属性值进行局部离散。由于作为参考涡轴发动机型号都是正在服役的世界上较先进的型号,因此,将每个属性指标离散为3个等级,对效益型指标表示好、一般、合格,对成本型指标表示低、一般、高,分别用3,2,1表示。将离散标准化后的数据建立一个二维信息表S=〈U,A,V,f〉,如表3所示。

表3 涡轴发动机型号发展评价信息表
确定出各属性的等价类:
U/IND(A)={{u1},{u2},{u3},{u4},{u5},{u6},
{u7},{u8},{u9},{u10},{u11},{u12}}
U/IND(A-{a1})={{u1,u5,u8},{u3,u10},{u2},
{u4},{u6},{u7},{u11},{u12}}
U/IND(A-{a2})={{u2,u7,u11},{u2},{u3},
{u4},{u5},{u6},{u8},{u9},
{u10},{u12}}
U/IND(A-{a3})={{u4,u6},{u1},{u2},{u3},
{u5},{u7},{u8},{u9},{u10},
{u11},{u12}}
U/IND(A-{a4})={{u9,u12},{u1},{u2},{u3},
{u4},{u5},{u6},{u7},{u8},
{u10},{u11}}
将式(4)~式(5)带入上面的等价类计算得:
SA(a1)=0.390SA(a2)=0.275
SA(a3)=0.113SA(a4)=0.122
利用式(6)确定出各个指标的权重w1~w4分别为0.4355,0.3050,0.1261,0.1334。将获得的权重结合式(7)计算出各设计方案的综合评价值,如表2最后一行所示。
从表2的评价结果可知,V2V1V3,由此可以看出整体上方案3最优,虽然它在系统效能方面稍差一些,但其寿命周期费用较低,研制风险较小,研制周期也较短。但是这三个方案之间的差距并不是很明显,在实际的涡轴发动机型号发展中可以根据实际需求,充分权衡各方面的利益情况下进行灵活选择。即可以以方案3为蓝本,将方案2中如何提升系统效能的优秀设计吸纳进来,设计出一套性能适中、开发和使用成本较低的涡轴发动机;也可以以方案2为蓝本,充分汲取方案1与方案2中对研制周期、费用、研制风险管理上好的方案,设计出一套高效能,开发与使用成本适中的涡轴发动机。
5 结语
本文构建了涡轴发动机型号发展评价指标体系,并应用粗糙集理论对世界上典型的同类型涡轴发动机的各项指标数据进行挖掘,以已知数据为驱动,用信息熵求得各指标的重要度,标准化处理后得到各指标的权重。该方法克服了传统主观权重判定法中对专家的过分依赖与客观权重判定法中可能出现的较大偏差,在相似型号较多的情况下可以通过增加同类型机的数量进一步提高权重确定的准确性与客观性。
[1] D.Mavris,D.DeLaurentis.An integrated approach to military aircraft selection and concept evaluation[R].AIAA,1995-95-3921:1-11.
[2] 熊少华,刘洪彬.雷达情报网作战能力评价指标体系研究[J].系统工程与电子技术,2000,22(3):94-95.
[3] 朱斯高,岳超源,赵勇.某型空舰导弹武器系统作战效能评估指标体系[J].华中科技大学学报,2005,22(9):126-128.
[4] 黄俊,武哲,孙惠中,等.作战飞机总体设计评价准则和评估方法研究[J].航空学报,2000,21(1):70-73.
[5] 刘大伟.武装直升机总体方案评估方法研究[D].南京:南京航空航天大学,2010.
[6] LU Hua,ZHOU De-yun.Research on Tactics Decision of Air-to-Ground Multi-target Combat[C]//International conference on computational intelligence and software engineering(CiSE),2009:1-5.
[7] 路录祥,王新洲.军用直升机型号发展工程[M].北京:航空工业出版社,2009.
[8] 周文松,蔡春,周卿吉,等.导弹武器系统方案评审指标体系研究[J].系统工程与电子技术,2001,23(11):18-21.
[9] WU Xiao-ping,AN Wei.System design theory and its application for the marine power systems[J].2000 Ⅱ GSSS-CB Workshop on “system,control,information” Methodologies and Applications,2006(6):1-6.
[10] 孟科,张恒喜,孟曼利.基于粗糙集的战斗机型号工程综合评价决策模型[J].航空学报,2006,27(4):641-645.
[11] C.Veleyuthan,K.Thangavel.Improved rough set algorithms for optimal attribute reduct[J].Journal of Electronic Science and Technology,2011(2):108-117.
[12] 菅利荣.面向不确定性决策的杂合粗糙集方法及其应用[M].北京:科学出版社,2008.
[13] Z.Pawlak,A.Skowron.Rough sets: Some extensions[J].Information Sciences,2007,177:28-40.
[14] Z.Pawlak.Rough sets and intelligent data analysis[J].Information Sciences,2002,147:1-12.
[15] 李远远,云俊.粗糙集理论在综合评价中的应用研究[J].中国管理科学,2009,17(10):192-196.
Comprehensive Evaluation Decision Model of Turboshaft Engine Based on Rough Set
ZHANG Yuanfa1JIANG Tao2LI Ronghui1
(1.Naval Command Automation Workstation,Beijing 100841)(2.Support Department,No.77126 Troops of PLA,Chongqing 402260)
An index system is proposed,which is based on quality standards of the new turboshaft engine program,integrated considering the system designation and needs of users.The rough set theory is applied to explore the index data of other turboshaft engines with similar capabilities which are used now in other countries.The conception of information entropy is used to compute the weighting coefficient of every index.This approach overcomes the subjectivity of traditional subjective way of weighting coefficient determination and overcomes potential error of impersonal way of weighting coefficient determination.At last,the comprehensive evaluation decision model of the turboshaft engine program development is set.The feasibility of the model is verified by a case study.
turboshaft engine,rough set,comprehensive evaluation,index system,information entropy
2014年8月5日,
2014年9月27日
章原发,男,助理工程师,研究方向:计算机通信。蒋涛,男,研究方向:综合保障。李荣辉,男,硕士,工程师,研究方向:计算机通信。
E917
10.3969/j.issn1672-9730.2015.02.002

