垂直电流元在深海中的电场强度算法推导*

张建春 王向军

(海军工程大学电气工程学院 武汉 430033)



垂直电流元在深海中的电场强度算法推导*

张建春 王向军

(海军工程大学电气工程学院 武汉 430033)

利用镜像法来研究腐蚀相关轴频电场在均匀、线性各向同性半无限大的导电介质中垂直方向所产生的电场强度,以垂直时谐电流元进行建模。通过矢量磁位A的引入对垂直时谐电流元在两层介质中某一固定点产生的电场强度推导出新的表达式,并验证其正确性。

导电介质; 电场强度; 垂直时谐电流元; 矢量磁位

Class Number TM15

1 引言

在海水为半无限大的空间中[1～2],本文将舰船等效为垂直电流元来进行建模。通过利用镜像法对海水中的垂直电流元半无限大、线性、均匀、各向同性的海水导体空间中任意点处的电磁场强度的表达式推导[3～4],本文所采用的镜像法求解矢量磁位的计算过程较为简单,避免了重复计算,并与数值计算方法[5]相结合,提高计算结果的正确性。最后通过与其他文献应用的算法得出的表达式[6～9]进行比较,并通过仿真验证其正确性。

2 腐蚀相关等效模型的建立及矢量磁位的引入

由Maxwell方程可知在线性、均匀、各向同性的介质中,时谐电磁场的电场强度E、磁感应强度B与矢量磁位的关系[4]如下:

(1)

(2)

(3)

其中:JS为外加电流元的电流密度,μ为媒质的磁导率,k2=-jωμ(σ+jωε),ω为场的角频率。

A=Azez

(4)

图1 半无限煤质中的垂直电流元

应用镜像法可以写出垂直电流元的矢量磁位在图1所示介质的内边界面上的边界条件和约束条件[4]。

边界条件:

(5)

约束条件:

(6)

式中,A1为垂直时谐电流元在空气的a′位置产生的矢量磁位,A2为海水的a位置产生的矢量磁位。

首先,计算在空气中任意点处产生的矢量磁位时,将海水看作是与空气具有相同介质,而空气中产生的矢量磁位仅由海水中的电流元产生,而在空气中不存在时谐电流元,即式(6)右边为零,通过边界条件和约束条件并应用快速Hankel变换[11]和欧拉公式很容易得到空气中的矢量磁位为

+d(λ,m)e-zu1]dλ

(7)

由图1可知,当z→∞时,A1z应有界,从而可得b(λ,m)=0,由边界条件(5)知,d(λ,m)只能取m=0,则

(8)

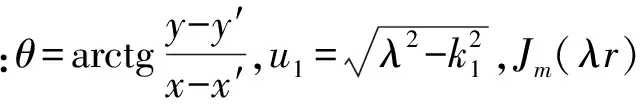
在求解海水中的矢量磁位时,将空气看做与海水介电常数相同的介质,在镜像z=h处放置一极低频垂直时谐电流元-JSδ(|R′|)ez作为等效电流元,则

+γ(λ,m)ezu1]dλ

(9)

+χ(λ,m)e-zu1]dλ

(10)

在z=h处,当z→∞时A2|z=h有界,则γ(λ,m)=0,并由边界条件知,m只能取0,从而得镜像源在a处产生的矢量磁位为

(11)

同理,在z=-h处由边界条件z→-∞时,A2|z=-h有界,则χ(λ,m)=0,从而根据边界条件知电流元在a处产生的矢量磁位为

(12)

由于海水中的矢量磁位由镜像电流元和电流元两者叠加而成,则在海水中产生的矢量磁位为

A2= (A2z|z=h+A2z|z=-h)ez

+β(λ,0)ezu2)J0(λr)dλez

(13)

将式(8)、式(13)分别代入边界条件式(5)便可确定d(λ,0)、α(λ,0)、β(λ,0)为

α(λ,0)=0

综上得

3 海水中垂直电流元在两层导电介质任意点的电磁场强度

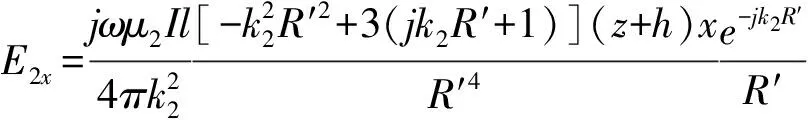
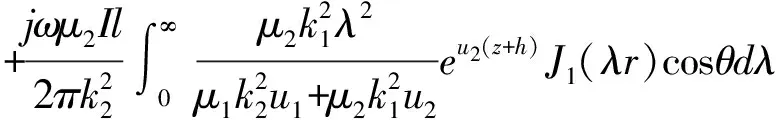
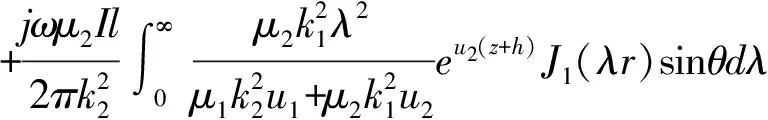
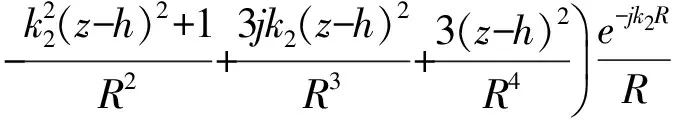
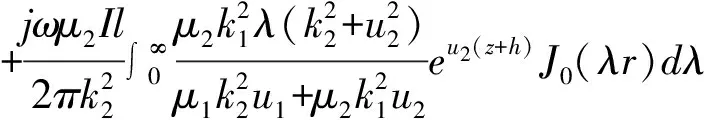
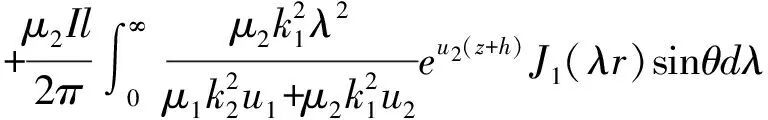
B2z=0

4 计算实例

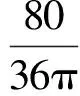
5 结语

本文用经典镜像法的方法结合在其他文献原有的研究基础上求解出垂直时谐电流元的矢量磁位的表达式,并根据经典的矢量磁位变量的引入推导出了位于海水中的垂直时谐电流元在海水中的电场强度表达式。

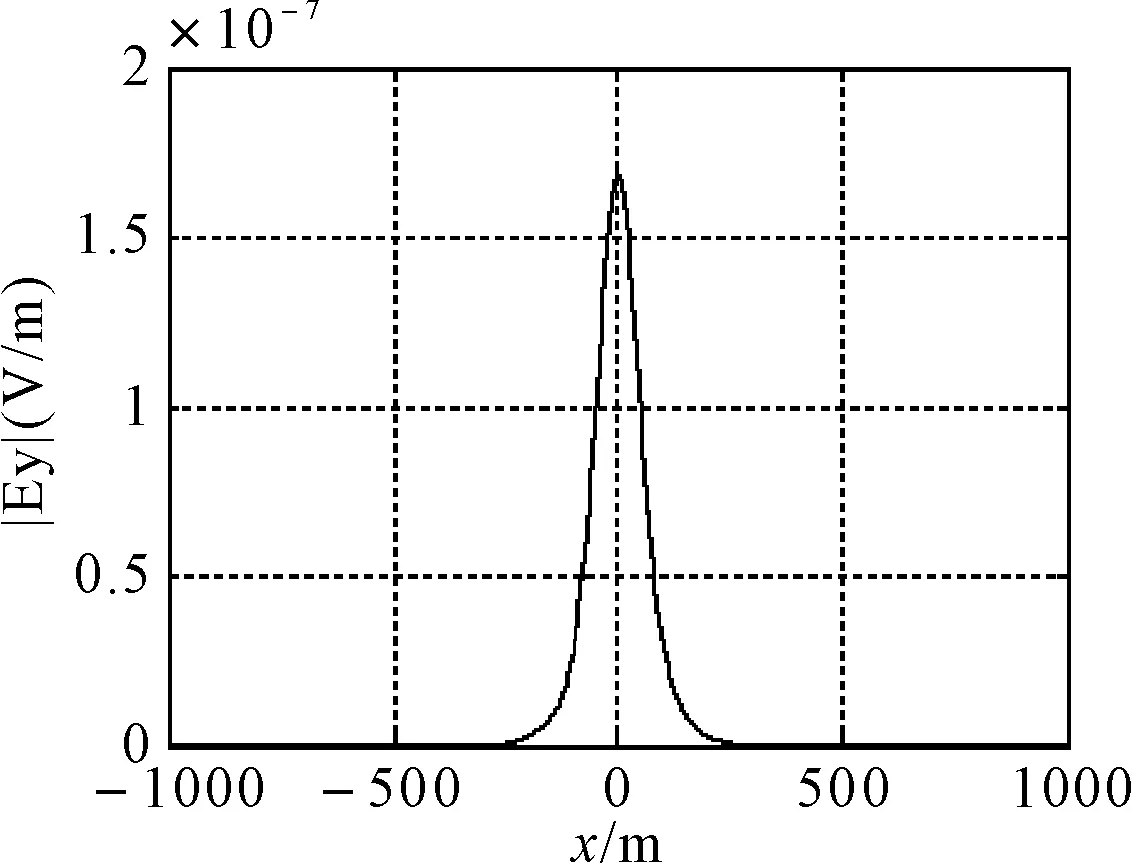
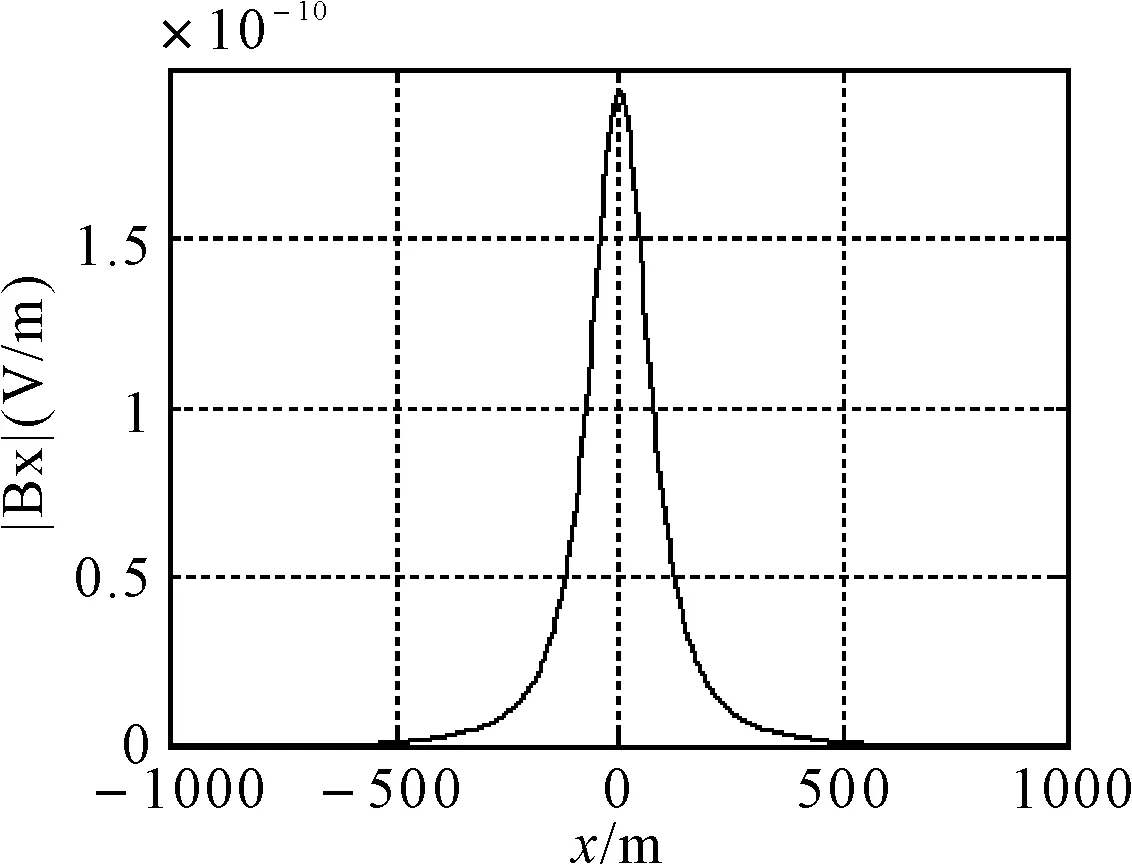
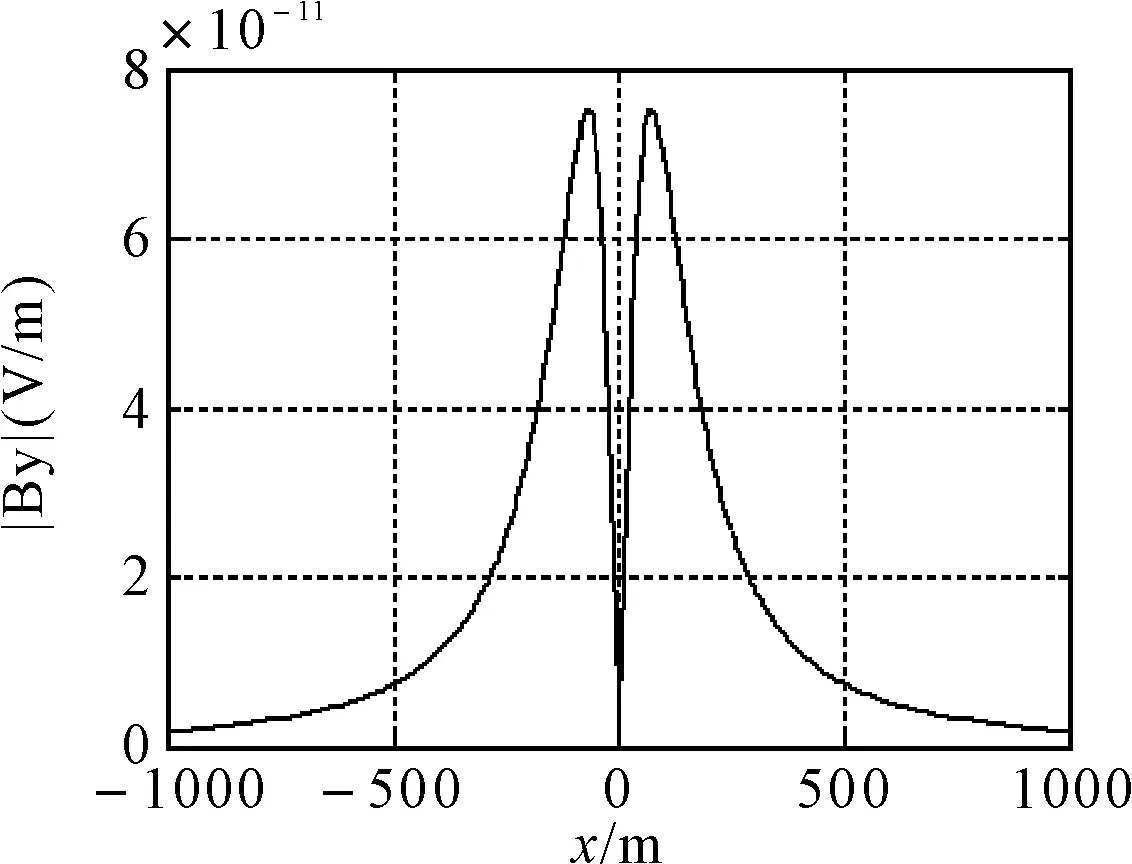
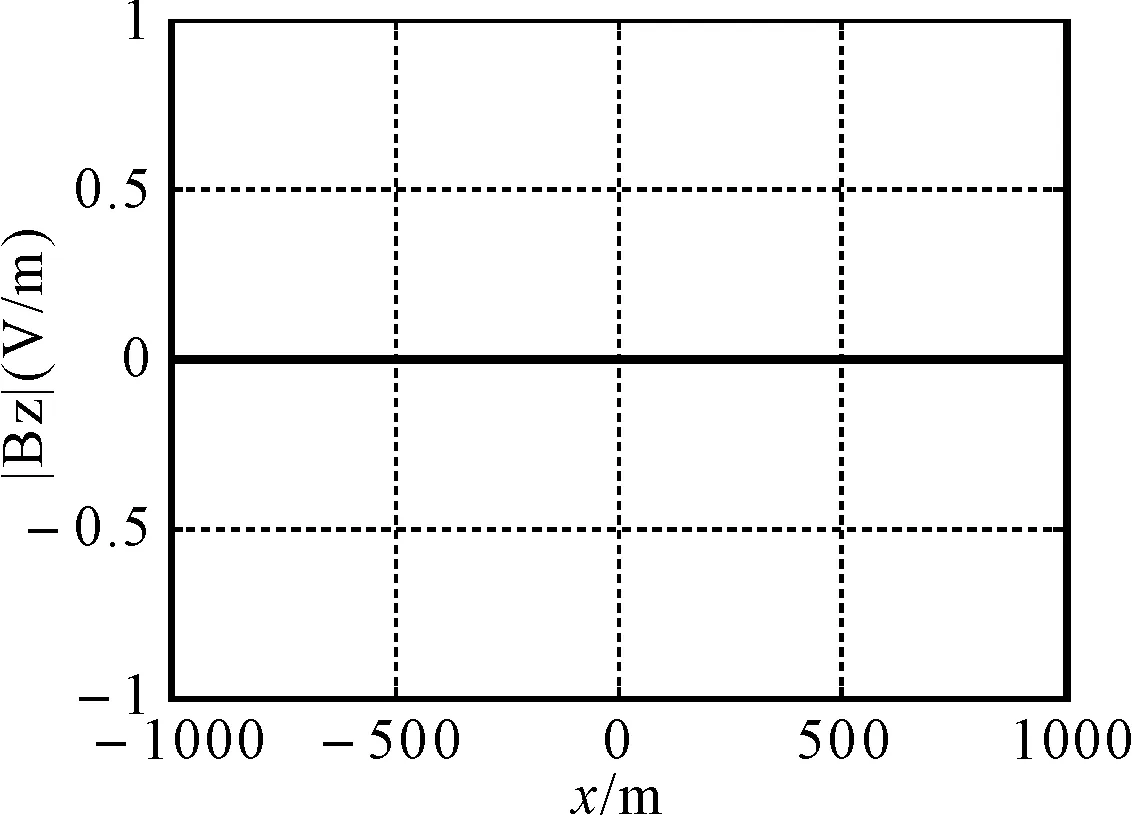
图2 海水中极低频时谐垂直电流元产生的电磁场幅值分布

该结果当μ1=μ2=μ且z轴反向时与文献[7]的结果是等价的,同时与文献[6]第五章推导出的结果也完全相等,本文采用的镜像法是将电流元整体进行镜像求解,且镜像源与电流元的求解方法相同,相对文献[6]采用的镜像法计算过程较简单,避免了重复的计算过程,使在求解矢量磁位时节省了很多时间。

[1] King R W P. Electromagnetic field of a vertical electric dipole over animperfectly conducting half-space[J]. Radio Science,1990,25(3):149-153.

[2] King R W P. The electromagnetic field of a vertical dipole in the presence of a three-layered region[J]. Radio Science,1994,29(1):97-113.

[3] Bannister P R. The image theory electromagetic fields of a vertical electric dipole in the presence of a conducting half space[J]. Radio Science,1982,17(5):1095-1102.

[4] 雷银照.时谐电磁场解析方法[M].北京:科学出版社,2000:108-148.

[5] 卢新城,龚沈光,陈新刚,等.水平n层导电介质中时谐垂直点偶极子的电磁场[J].地球物理学进展,2004,19(3):596-601.

[6] 徐建华,胡文宝,李鹏翔.层状导电媒质中垂直电偶极子的场[J].江汉石油学院学报,1992,14(1):41-44.

[7] Peter R B, Rene L D. Simple Expression for Vertical Electric Dipole Quasi-static Range Subsurface-to-Subsurface and subsurface-to-air Propagation[J]. Radio Science,1978,13(2):501-507.

[8] 毛伟,林春生.两层介质中运动垂直时谐偶极子产生的电磁场[J].武汉理工大学学报(交通科学与工程版),2011,10(5):1081-1085.

[9] 汪小娜,肖昌汉,王向军,等.运动潜艇的感应电场分布[J].海军工程大学学报,2012,24(4):7-10.

[10] 卢新城,龚沈光,孙明.轴转动调制腐蚀电流产生的极低频磁场的测定[J].兵工学报,2004,25(5):544-546.

[11] 胡俊,聂在平.索末菲尔德积分新方法——快速汉克尔变换[J].电子学报,1998,26(3):126-128.

Arithetic Derivation about Electric Field Intensity of Vertical Current in the Deep Sea

ZHANG Jianchun WANG Xiangjun

(College of Electronic Engineering, Naval University of Engineering, Wuhan 430033)

Image method is used to study the electric intensity related to shaft-rate of corrosion in the conductive medium, which is half infinite field of hoegeneous, linear and in the same nature, modeled by vertical harmonic current. The new electricity intensity expression about some fixed point in two layer medium, which is produced by vertical harmonic current, is deduced by introducing the magnetic vector potential A, and its correctness is verified at last.

conductive medium, electric intensity, vertical harmonic current, magnetic vector potential

2015年4月1日,

2015年5月27日

张建春,男,硕士研究生,研究方向:电磁环境与防护技术。王向军,男,博士,教授,硕士生导师,研究方向:电磁环境与防护技术。

TM15

10.3969/j.issn.1672-9730.2015.10.043