三平移并联机器人正解解析法的研究

蒙运红 金 逸 黄 进

(1.华中科技大学机械学院 武汉 430074)(2.长江科学院仪器所 武汉 430010)



三平移并联机器人正解解析法的研究

蒙运红1金 逸2黄 进1

(1.华中科技大学机械学院 武汉 430074)(2.长江科学院仪器所 武汉 430010)

论文对3-PUU三平移并联机器人进行了运动学建模,并通过置换消元法推导出该机构位置正解的解析式,实验验证了正解算法的正确性,并利用正解解析式得出了该机构一些运动特性,为该类型并联机器人的实时反馈控制提供了理论依据。

三平移; 机构; 并联; 机器人; 运动学; 正解

Class Number TP29

1 引言

并联机构运动学正解是研究进行运动学分析的基础[1～3],其解法主要有数值法和解析法。数值法的速度慢、并且不一定能求出所有可能的解,解析法求解需要建立复杂的数学模型,其公式推导及计算过程相当繁杂,不同的机构复杂度也有很大差异。在对称结构的三自由度并联机构正解求解方法中,很多学者[4～7]分别求出了平面机构3-RRR、3-RPR和空间机构3-RPR和3-RPS位姿正解的解析式。鲁开讲等[8]和高征[9]采用不同方法求出球面三自由度并联机构位姿方程的全部解。针对非对称结构,刘治志等[10]求出了2-UPS&PRR位姿正解的解析解,郭玉等[11]对过约束的2-RTR&RSR机构进行了位姿正解建模,并求出其数值解。黄俊杰[12]等结合遗传算法求出3-PRS并联机构数值解。本论文对图1所示的具有对称结构的3-PUU三平移并联机器人的运动学正解进行了推导,得出了其终端执行器位置计算的解析表达式,为该种类型机器人运动的适时控制提供了理论基础。

2 三平移并联机器人运动学位置正解

如图1所示,电机带动三滑块上下运动,通过12个虎克铰链和三个平行四边形机构,带动终端执行器沿水平(X)、垂直(Y)和铅垂(Z)方向移动,终端执行器上加有旋转主轴,刀具与主轴相连。其机构运动简图如图2所示。A1,A2,A3分别为三滑块上万向节铰链中心,C1,C2,C3为丝杠中心线与工件台表面交点,B1,B2,B3为动平台上万向节铰链中心。D1,D2,D3为滑块上万向节铰链中心在工作台表面的投影。△A1A2A3,△B1B2B3,△D1D2D3均为等边三角形。设△D1D2D3的内心为固定坐标系原点O,与D1D2平行的方向为X轴方向,向右为正。垂直向里为Y轴正,竖直向上为Z轴正,A1D1=s1,A2D2=s2,A3D3=s3。设△B1B2B3的内心为动坐标系原点o,与B1B2平行的方向为x轴方向,向右为正。垂直向里为y轴正,竖直向上为Z轴正。x,y,z与X,Y,Z三轴分别相互平行。

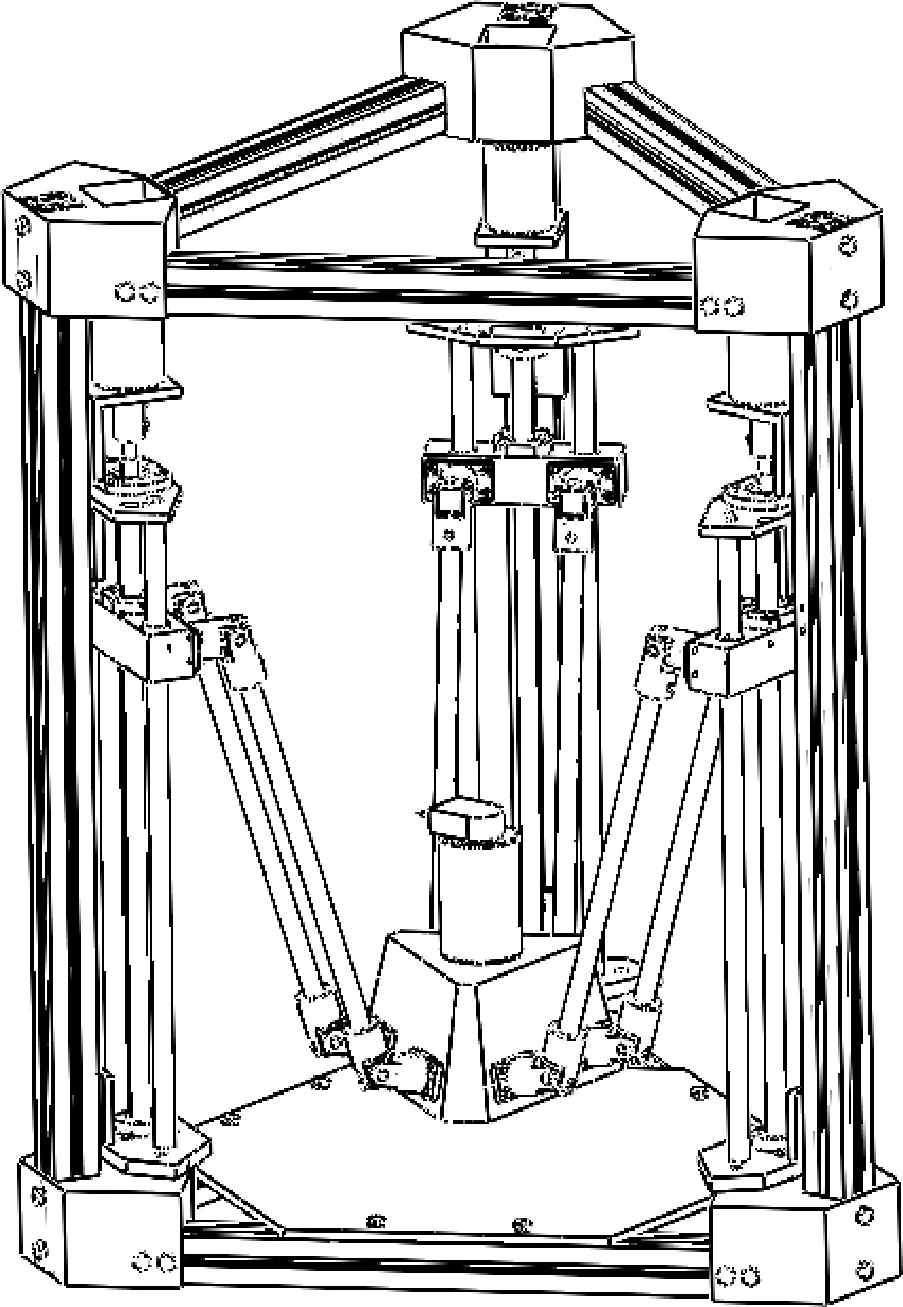
图1 三平移并联机构

图2 机构运动简图及坐标系定义

并联机器人正解就是根据三滑块的位移s1,s2,s3,求出动坐标系上刀尖点在固定坐标系下的的坐标(x,y,z),即求(x,y,z)=F(s1,s2,s3)。

机构运动学尺寸为:固定平台三角形边长l1=lD1D2=lD2D3=lD3D1,动平台三角形边长l2=lB1B2=lB2B3=lB3B1,连杆长度,即万向节铰链中心的距离l3=lA1B1=lA2B2=lA3B3,刀具加工点到万向节铰链中心所在平面的距离l4。

三滑块万向节铰链中心Ai(xAi,yAi,zAi),i=1,3,在固定坐标系下的坐标可表示如下:

根据定长条件可得:

(1)

其中Bi(xBi,yBi,zBi),i=1,3为动平台三个铰链中心在固定坐标系O-XYZ下的坐标。

因为动平台运动中始终水平,故zB1=zB2=zB3

又有△B1B2B3为等边三角形,故

(xB1-xB2)2+(yB1-yB2)2=(xB2-xB3)2+(yB2-yB3)2

=(xB3-xB1)2+(yB3-yB1)2

刀尖点的坐标可以分别表示为

将Ai(xAi,yAi,zAi)和Bi(xBi,yBi,zBi)代入方程(1),可得(x,y,z)关于(s1,s2,s3)的方程如下:

设L=l1-l2,zB=zB1=zB2=zB3=z+l4,则上式可简化为

(5)

式(2)+式(3)-2×式(4)化简得:

(6)

展开化简后得:

±分别对应B点处于A点之上或之下的位置。如图所示机构,B点处于A点之下,故取

(7)

将式(7)代入式(5)和式(6)即可求出x、y的值,从而求得三平移并联机器人位置正解的解析式。

3 实验验证

实验室中机器机构运动学尺寸如下:

l1=371mm,l2=175mm,l3=406mm,l4=113mm

实验开始,调整三轴在同一水平面内,即三滑块初始位置s1=s2=s3=533mm;使Ⅰ轴滑块往上运动20mm,Ⅱ轴滑块往下运动20mm,Ⅲ轴不动。则初始和结束两个状态的计算结果如表1所示,实际测量结果如表2所示。

表1 正解计算结果

表2 实测结果

由表1、表2可以看出计算结果和实测结果基本符合,由于所用测量工具为卷尺,故存在一定误差,但说明本论文的正解算法是正确的。

根据三平移并联机器人位置正解的解析式,可以得到该并联机器人的一些运动特性。

1) 当s1=s2=s3=s时,x=y=0,

说明若希望刀尖沿Z轴运动,只需使三滑块同速同向运动,此时刀尖与三滑块同速同向运动。

2) 当s1=s2时,由式(5)x=0。

说明当相邻两轴同高运动时,或该两轴不动第三个轴单独运动时,刀尖在固定坐标系下的投影沿Y轴方向运动,或者说在OYZ平面内运动。

4 结语

论文首先用输出点即刀尖点的坐标表示动平台上三个铰链点的坐标,再根据定长条件得到刀尖点坐标与输入位移关系的三个方程,通过置换消元法,求得三平移并联铣床刀尖点的位置坐标解析式,实验结果验证了解析解的正确性,并利用解析解得出了该机构运动的一些运动特性。为该类型并联机器人的实时反馈控制提供了理论依据。

[1] 张曙,U.Heisel.并联运动机床[M].北京:机械工业出版社,2003.

[2] 黄真,孔令富,方跃法.并联机器人机构学理论及控制[M].北京:机械工业出版社,1997.

[3] 季晔,刘宏昭,原大宁,等.并联机构位置正解方法研究[J].西安理工大学学报,2010,26(3):277-281.

[4] 周琪甦,邵仁玉.平面三自由度并联机构的正解分析[J].南通工学院学报(自然科学版)2002,1(2):79-81.

[5] 曹清林.特殊结构尺度三自由度平面并联机构正解分析[J].机械科学与技术,2003(6):977-979.

[6] Chung J, Yi B J, Oh S. A Foldable 3 DOF Parallel Mechanism with Application to a Flat panel TV Mounting Device[J]. IEEE Transactions on Robotics,2009,25(5):1214-1221.

[7] 吴昌林,陈航.几种三自由度并联机构的位置正解方法[J].机床与液压,2006(5):71-73.

[8] 鲁开讲,牛禄峰,雷文莉,等.球面三自由度并联机构位姿正解的研究[J].机械设计,22(1):59-61.

[9] 高征,高峰.球面3自由度并联机构的正解分析新方法[J].机械设计与制造,2006(9):122-124.

[10] 刘治志,罗玉峰,杨廷力,等.一种新型空间三自由度并联机构及其位置正解[J].机械设计与制造,2008(7):15-16.

[11] 郭玉,赵新华,李彬.一种过约束3自由度并联机构的位置正解研究[J].天津理工大学学报,2012(2):20-22.

[12] 黄俊杰,赵俊伟,等.3-PRS并联机构位置正解分析[J].河南理工大学学报(自然科学版),31(4):434-436.

Analytic Positive Solution Algorithm of 3-d.o.f Translational Parallel Robot

MENG Yunhong1JIN Yi2HUANG Jin1

(1. School of Mechanics, Huazhong University of Science & Technology, Wuhan 430074) (2. Instrument Institute, Yangtze River Scientific Research Institute, Wuhan 430010)

The analytic expression of the positive solutions of mechanism position of the 3-PUU 3-d.o.f translational parallel robot is derived by kinematics modeling and the displacement elimination in this paper. The analytic positive solution algorithm is verified by the experiments, and used to obtained some movement characteristics of the mechanism, and provides theory basis for real-time feedback control of this type of parallel robot.

3-d.o.f translational, mechanism, parallel, robot, kinematics, positive solutions

2015年4月10日,

2015年5月29日

国家自然科学基金项目(编号:51275363)资助。

蒙运红,女,博士,高级工程师,研究方向:机械设计及理论。金逸,男,高级工程师,研究方向:机械制造及工艺设备自动化。黄进,女,高级工程师,研究方向:机械制造及工艺设备自动化。

TP29

10.3969/j.issn.1672-9730.2015.10.017