基于MATCONT的潜艇垂直面操纵运动稳定性与分叉分析*
吕帮俊 彭利坤 何曦光
(海军工程大学动力工程学院 武汉 430033)
基于MATCONT的潜艇垂直面操纵运动稳定性与分叉分析*
吕帮俊 彭利坤 何曦光
(海军工程大学动力工程学院 武汉 430033)
基于Matlab数值分岔分析工具箱MATCONT对潜艇高速机动时的运动稳定性与分岔问题进行了研究。分析了潜艇重心坐标和尾升降舵角变化时的单参数分岔,搜索到系统的鞍结分岔和BP分岔点,通过垂直面非线性运动方程数值积分的动态仿真,验证了动态仿真与数值分析结果的一致性。
潜艇; 垂直面运动; 稳定性与分岔; MATCONT
Class Number U661; TP13
1 引言
确定潜艇运动稳定性的传动方法主要集中在直线基准运动附近小扰动情况下,基于线性近似模型,使用垂直面和水平面两个独立的稳定性指标来判断[1]。
潜艇水下空间机动本质上是一种非线性运动,因此描述潜艇运动的数学模型也应该是非线性的。现代潜艇的朝着大潜深、高航速的方向发展,尤其是战术训练中往往需要潜艇在垂直面以高航速、大舵角作强机动,这些对潜艇的操纵控制技术提出了更高的要求。随着航速的提高,水动力的非线性、不对称性和耦合特性使得潜艇的空间机动呈现高维复杂非线性特征,而目前针对高维非线性系统复杂动力学特性的研究尚不充分。美国海军研究生院的Papoulias等[2~3]应用非线性动力学及非线性数值分析的相关理论对潜艇在低速深度控制下水平舵的多稳态解,自由正浮力上浮中的运动稳定性等问题作了系统分析。戴余良等[4]应用奇异性和分叉理论,采用同伦延拓数值计算方法,研究了航速、升降舵、方向舵和剩余浮力等因素对潜艇应急上浮过程运动稳定性的影响。王晓玢等[5]以葛特勒方程为基础,研究潜艇处于高速大舵角的运动模态,为强机动情况下潜艇操纵及自动控制系统的设计提供理论。
本文采用基于Matlab的数值分叉分析工具箱MATCONT,针对潜艇垂直面非线性运动模型进行稳定性和分叉分析,重点研究高航速下操纵尾升降舵角以及重心位置变化情况下模型的稳态解和分叉情况,为强机动下潜艇的运动稳定性和航行安全性提供参考依据。
2 数学模型
考虑潜艇的受力,其垂直面运动二阶非线性方程:
-(xGW-xBB)cosθ-(zGW-zBB)sinθ

η=0.012n/u
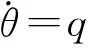
其中采用的坐标系和主要参数如图1所示,u,w,q分别为潜艇的纵向速度、垂向速度和纵倾角速度;θ,ζ分别为潜艇的纵e倾角和深度;δb,δs分别为潜艇的首、尾升降舵角;W,B分别为潜艇的重力和浮力;xG,B,zG,B分别为潜艇重心和浮心的位置坐标,n为螺旋桨转速,Cd0为潜艇的阻力系数。
3 同伦延拓非线性数值计算方法
为解决应用分岔理论对非线性系统进行分岔分析时,定量搜索分岔点、判断分岔点及确定分岔点处新分支方向等数值分析难题,比利时Govaerts[6]等开发了基于MATLAB—GUI平台求解参数化非线性动力微分方程的分岔分析工具箱MATCONT,它可以计算平衡点曲线、极限点、Hopf分岔、极限环等,其算法的核心是基于同伦延拓的非线性数值计算方法。

图1 坐标系和运动参数
对于含参数的常微分方程系统


如果系统的Jacobi矩阵在平衡点处存在零特征值,则平衡点是奇异的,在奇异点处可能出现静态分岔。平衡点静态分岔问题实际上是平衡方程的多重解问题。
同伦延拓方法是求解非线性问题的一种非常有效的方法,它克服了传统迭代法局部收敛的弱点,对初值的选取没有严格限制,能够全局收敛,可以求出问题的全部解。传统的求解方法如迭代法、消去法等存在的最大问题是依赖于初值的选取,初值选择不当常常导致迭代过程不收敛,而且很难求出全部解。因此,同伦延拓方法被誉为二十世纪数学研究中一项带突破性的新成果。

为了求解非线性方程组f(x)=0,其中光滑映射f:Rn→Rn,x=[x1,x2,…,xn]T,选取具有已知零点的光滑辅助映射g:Rn→Rn,将其与映射f构成一线性同伦函数H:Rn×Rn→Rn,使得H(x,0)=g(x)和H(x,1)=f(x),典型的同伦函数为
H(x,λ)=λ·f(x)+(1-λ)·g(x)λ∈[0,1]
对于同伦方程组H(x,λ)=0,当λ=0时,其解与辅助方程组g(x)=0的解相同;让同伦参数λ从0逐渐变化到1,并跟踪同伦方程组的解,则当λ=1时,同伦方程组的解便是待解方程组f(x)=0的解。
4 潜艇垂直面操纵运动分叉分析
1) 计算条件:δb=δs=0,n=1000rpm,W=B=13400N,xB=xG=zB=0,潜艇纵倾角随重心坐标zG变化的稳态解和分岔情况如图2所示。
图3为以zG为同伦参数时特征根实部的变化情况,zG的变化范围为[-3.5,3],在zG=0附近系统特征值实部的正负号发生了改变,因此zG>0时平衡点稳定,zG<0时平衡点不稳定。研究平衡点在BP点的分岔情况,发现在BP点处与原解曲线垂直的方向上出现了新的两支解曲线,图2所示。在这两支新的解曲线上,纵倾角急剧增加。这是因为重心zG=0时,重心与浮心重合,稳定中心高及纵倾扶正力矩为零,稍有扰动,潜艇姿态就会发生无法预料的剧烈变化,这是应当避免的情况。
图4中给出了分岔点BP前后潜艇纵倾角随时间的动态响应曲线,其中实线和虚线分别对应于zG=0.1和zG=-0.1时,潜艇初始纵倾角均为θ=10°,可以看出zG=0.1时潜艇纵倾角可以回复到零,而zG=-0.1时系统是发散的。
2) 计算条件:δb=0,n=1000rpm,W=B=13400N,zG=0.061m,xB=zB=0,图5中,实线、虚线和点划线分别表示当xG=0、xG=1%L和xG=-1%L时,潜艇纵倾角随尾舵角δs变化的稳态解和分岔情况,其中L为艇长。

图2 纵倾角随zG的变化

图3 系统特征值随zG的变化

图4 分岔点前后潜艇的纵倾响应
当xG=0,δs=±0.93°时,系统发生了鞍结分岔,图6为相应的系统特征值实部的变化情况,分岔点处系统的特征值为零,而在分岔点附近系统特征值实部的正负号发生了改变,系统的稳定性也随之发生变化。在鞍结分岔点潜艇纵倾角为90°,此时艇的重心和浮心在同一水平面内。当纵倾角小于90°时,浮心在重心之上,此时重力和浮力产生的合力矩为扶正力矩,在此力矩的作用下,潜艇定深航行时因为扰动产生的小量纵倾能够回复到无纵倾状态;而当潜艇纵倾角大于90°时,重心在浮心之上,此时重力和浮力产生的合力矩为倾覆力矩,在此力矩的作用下,潜艇的小量纵倾将进一步增大,导致系统不稳定。当xG=1%L时,潜艇的重心向艇首方向移动,从而引起了纵向稳定中心高的增大,因此分岔点对应的尾舵角值也有所增大,另一方面,由于重心向艇首方向的移动,当潜艇首倾使得重心和浮心在同一水平面时对应的纵倾角将大于90°,而当潜艇尾倾使得重心和浮心在同一水平面时对应的纵倾角将小于90°,所以图5中δs>0时对应的分岔点位于xG=0时的分岔点的右下方,δs<0时对应的分岔点位于xG=0时的分岔点的左下方。对于xG=-1%L时分岔点的移动情况可用类似的方法进行分析。

图5 对于不同xG纵倾角随δs的变化
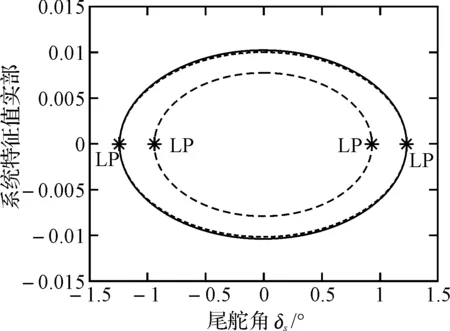
图6 对于不同xG系统特征值随δs的变化
图7 分岔点前后潜艇的纵倾响应
图7给出了xG=0时,右侧分岔点前后潜艇纵倾角随时间变化的动态相应曲线,进一步说明了由静态分岔引起的状态突变的响应过程。
5 结语
基于Matlab的数值分岔分析工具箱MATCONT,研究了潜艇高航速下垂直面非线性运动的稳定性和分岔问题。分别以尾升降舵角和重心垂向坐标为同伦参数,分析了某模型艇垂直面运动的稳态解和分岔情况,所得分岔点以及分岔点附近运动稳定性的变化情况与目前已知的潜艇运动规律一致,从而验证了进一步利用该方法探讨潜艇空间高速非线性运动稳定性和分岔问题的可行性,为强机动下潜艇的运动稳定性和航行安全性提供参考依据。
[1] 施生达.潜艇操纵性[M].北京:国防工业出版社,1995.
[2] Papoulias F A, Aydin I. Out of plane solutions and bifurcations of submersibles in free positive buoyant ascent[J]. Journal of Ship Research,1994,38(4):259-271.
[3] Papoulias F A. Nonlinear studies of dynamic stability of submarines in the dive plane[J]. Journal of Ship Research,1995,39(4):347-356.
[4] 戴余良,王长湖,苗海,等.潜艇水下运动稳定性非线性分析研究[J].船舶力学,2011,15(8):844-852.
[5] 王晓玢,孙尧,莫宏伟.潜艇操纵运动分岔突变特性[J].工程力学,2009,26(10):252-256.
[6] Govaerts W, Kuznetsov Yu A, Witte V De, et al. MATCONT and CL MATCONT: Continuation toolboxes in matlab[EB/OL]. http://www.sourceforge.com/,2011-08.
Stability and Bifurcation Analysis of Submarine Motion in Dive Plane Based on MATCONT
LV Bangjun PENG Likun HE Xiguang
(College of Power Engineering, Naval University of Engineering, Wuhan 430033)
The problem of dynamic stability and bifurcation of submarine motion in the dive plane is examined utilizing numerical bifurcation tool box MATCONT based on Matlab. The signal parameter bifurcations analysis including submarine stern plane deflection and coordinates of submarine center of gravity are studied respectively. The saddle-nod bifurcation and branch point are obtained, and the stability analysis results are verified by direct numerical integration of the nonlinear equations.
submarine, motion in vertical plane, stability and bifurcation, MATCONT
2014年7月7日,
2014年8月14日
吕帮俊,男,博士,讲师,研究方向:潜艇操纵。
U661; TP13
10.3969/j.issn1672-9730.2015.01.015

