舰用12脉波整流器直流侧谐波分析

秦萌涛,宋文武，黄　琛

(电磁兼容性国防科技重点实验室, 湖北 武汉 430064)

舰用12脉波整流器直流侧谐波分析

秦萌涛,宋文武，黄琛

(电磁兼容性国防科技重点实验室, 湖北 武汉 430064)

摘要：针对现代舰艇直流电网的谐波问题，在分析负载并联的12脉波整流站基本工作原理和理想条件下特征谐波的基础上，采用调制理论和傅里叶分析方法对交流侧电压不对称、触发脉冲间隔不对称和变压器漏感引起的换相问题等非理想条件下，整流系统直流侧输出电流(电压)的谐波情况进行理论分析和仿真验证。计算和仿真结果表明：交流侧电压的不对称和触发脉冲间隔的不对称会导致12脉波整流系统直流侧输出电流(电压)的2，4次等低次非特征谐波显著增多，而考虑变压器漏感引起的换相时，则直流侧输出将含有6 n次谐波分量且其他各次非特征谐波含量和总的谐波畸变率增加很多。

关键词：非特征谐波;12脉波整流;开关函数;傅里叶分析

0引言

舰船综合电力系统(Integrated Power System, IPS)的核心思想是电力集成。它将舰船电能的产生、输送、分配、变换等综合技术应用于现代舰船电力推进和新概念武器发射[1-2]。舰船综合电力系统具有效率高、损耗低、可靠性和可维护性强的优点，极大地提高了舰艇的机动性能和作战性能等。但由此而配载的工作于非线性状态下的电子设备将大量谐波和无功分量注入了电力系统，尤其是现代电力电子器件因其开关动作引起的非线性工作模式。

用于直流配电的整流装置正是电网中最主要的谐波源之一。当直流系统处于理想稳态对称运行的情况，整流器只产生特征谐波。但实际中，由于三相电压不对称、换流变压器三相参数不平衡、触发脉冲不对称以及多脉波整流系统中移相变压器结构不对称等原因，直流侧和交流侧还会出现其他次数的非特征谐波。谐波分析方法主要分为时域法和频域法，文献[3-4]采用基于Newton-Raphson法同时计算基波和谐波潮流，但要求谐波源电压和电流已知，且方程组Jacobi矩阵十分复杂，计算量大。文献[5-8]提出了谐波导纳矩阵法，该方法用一频域耦合导纳矩阵模拟谐波产生特性，考虑了系统和谐波的相互耦合，清晰地展现了谐波产生机理，并且其模型精确、不需迭代，相比其他频域方法具有优势。但由于模型精细，耦合导纳矩阵元素取决于电路参数和系统运行参数，由于系统通常都是时变的，矩阵每次都需重新计算，工作量过大。本文采用基于调制理论和时域波形傅里叶分析的方法，对舰艇上常用的12脉波整流系统直流侧谐波特性进行分析。

1理想条件下的直流侧特征谐波

假设：可认为整流器工作于理想状态[9]；交流侧的电压是三相对称的正弦电压，即只含有正序分量；各相的交流侧阻抗完全相等；直流侧的平均电流恒定；三相的触发脉冲对称且间隔相等；不考虑晶闸管的换相过程。

12脉波并联全桥整流原理如图1所示。

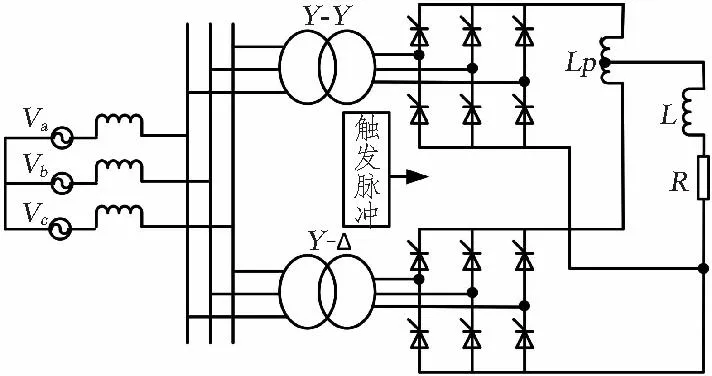
图1　12脉波并联全桥整流器Fig.1　12-pulse wave parallel full bridge rectifier

因二次侧星型(Y)和三角形(Δ)连接的2组三相整流桥输出电压之间有1个固定π/6的相移[10]，若将整流器直流输出侧串联或并联连接时，则可形成12脉动的直流电压波形。

设输入三相正弦电压为：

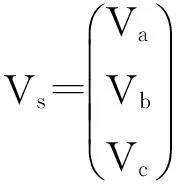
(1)

式中：V0为各相电压的有效值；ω0为电网电压的角频率；t为相应的周期。设直流侧负载为电阻R和电感L的串联，Lp为平衡电抗器。

根据调制理论[11-14]，直流侧输出电压VDC是由输入侧三相电压Vs经电压开关函数SV调制得到的，即有：

VDC=SV(ωt)·Vs，

(2)

式中：SV(ωt)=[Sa(ωt),Sb(ωt)为开关函数,Sc(ωt)]为一个行向量，它的每个元素与开关器件开通和关断状态相对应。设整流器的触发角为α(≤2π/3)，不考虑换相过程，则开关函数的时域表达式为：

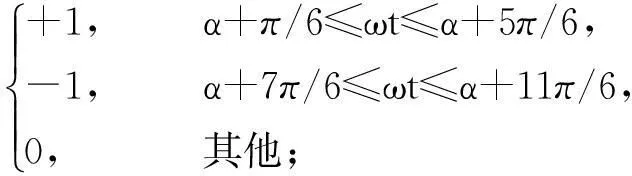
Sb(ωt)=Sa(ωt-2π/3),Sc(ωt)=Sa(ωt+2π/3)。

(3)

图1中二次侧星型(Y)连接的直流输出电压1个工频周期为6脉动，其时域表达式为：

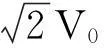
ω0t∈[α+π/6,α+π/2]。

(4)

为分析方便，假设α=0，对式(4)进行傅里叶分解得到：

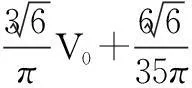
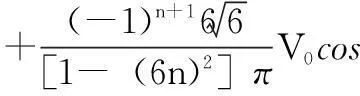
(5)

二次侧三角形型(Δ)连接的直流输出电压为:

VDC2(ωt)=VDC1(ωt-π/6)，

ω0t∈[α+π/6+π/6,α+π/2+π/6]。

(6)

两组三相整流桥经平衡电抗器后输出电压的值为：

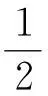
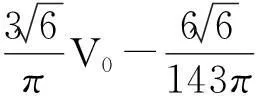
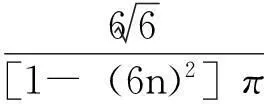
(7)

因此，根据电路理论，总输出电流为:

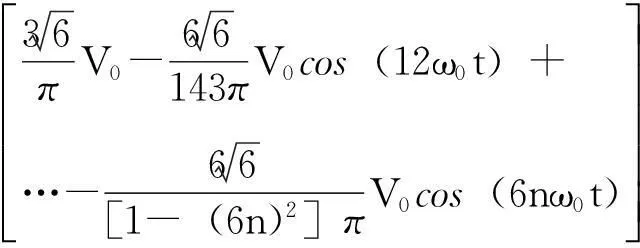
(8)

式(8)说明，理想情况下，12脉波整流器输出电流仅含12n(n=1,2,3…)次谐波分量，且幅值随频率增大以1/(6n2)的速度较快地衰减。

对于α≠0(α≤π/3)，按照同样的方法可得到相同的结论。

2非理想条件下的直流侧非特征谐波

2.1　电网负序分量引起的非特征谐波

电网实际运行时，整流器输入交流电压常存在不对称现象，主要体现在负序电压的存在。假设各相相角不变，则由对称分量法，输入电压可分解为零序分量Vo、各自对称的正序分量Vp与负序分量为Vn的和，即：

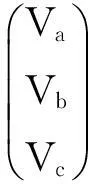
(9)

根据调制理论，可得到：

VDC=SV(ωt)·Vs=SV(ωt)·Vo+SV(ωt)·Vp+

SV(ωt)·Vn。

(10)

其中

第1项为零序分量整流输出的直流电压。由于开关函数三相对称，故有：

SV(ωt)·Vo=Sa·V0∠φ+Sa·V0∠φ+Sa·V0∠φ=

(Sa+Sa+Sa)·V0∠φ=0；

(11)

第2项SV(ωt)·Vp为正序分量整流输出的直流电压，其谐波分析方法与理想条件下相同，谐波次数仍为12n(n=1,2,3…)，只是幅值有所不同；

第3项SV(ωt)·Vn为正序分量整流输出的直流电压，设：

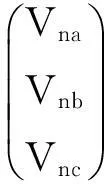
(12)

则经过开关调制，二次侧星型(Y)连接的直流输出电压的周期为T0/2，其时域表达式为：

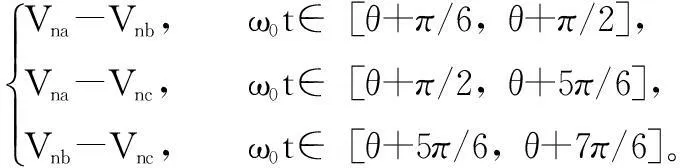
(13)

对式(13)进行傅里叶级数展开(假定θ=0)可得：

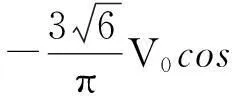
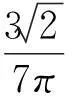
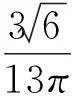
(14)

则二次侧三角形型(Δ)连接的直流输出电压为:

VDC2(ωt)=VDC1(ωt-π/6)，

ω0t∈[α+π/6+π/6,α+π/2+π/6]。

(15)

2组三相整流桥经平衡电抗器后输出电压的时域值为：

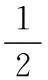
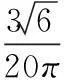
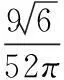
(16)

因此，根据电路理论，总输出电流为:

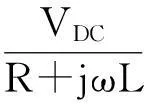
(17)

式(17)说明，负序分量激励下，12脉波整流器输出电流含2n(n为自然数，且n不为3的整数倍)次谐波分量，其中2次谐波幅值最大，且各次谐波幅值随频率增大较快地衰减。

因此，通过以上对式(10)中3项的傅里叶分析可得出如下结论，当三相电压中出现负序分量时，12脉波整流的直流输出端会出现2n(n为自然数，n≠6k(k为奇数))次谐波分量，谐波含量较三相电压对称时有明显的增加。

2.2　触发脉冲不对称引起的非特征谐波

当触发脉冲不对称时，也可将开关函数分解为零序分量、各自对称的正序分量和负序分量之和[15]，即：

SV(ωt)=SVo(ωt)+SVp(ωt)+SVn(ωt)。

(18)

假设三相电压Vs对称，同理根据调制理论，有：

VDC=SV(ωt)·Vs=SVo(ωt)·Vs+SVp(ωt)·Vs+

SVn(ωt)·Vs。

(19)

与三相电压存在零序和负序分量的情况相同，由于Vs三相对称，式(19)中第1项SVo(ωt)·Vs为0；第2项SV(ωt)·Vp为正序分量整流后相应的直流分量，其谐波分析方法与理想条件下相同，其包含的谐波次数仍为12 n(n=1,2,3…)，只是幅值有所不同；第3项为负序分量整流后相应的直流分量，其谐波分析方法与三相电压存在负序分量相同，其包含的谐波次数为2 n(n为自然数，且n不为3的整数倍)次。因此，式(19)中含有2n(n为自然数，且n≠6k(k为奇数))次谐波分量。

综合第2.1和第2.2节的分析和计算，可得出结论：当三相电压和触发脉冲均不对称时，12脉波整流直流输出侧将出现2n(n为自然数)次谐波分量，其中电网中的正序分量产生12n(n=1,2,3…)次特征谐波，负序分量产生的其余次数谐波为非特征谐波。

2.3　换相重叠角引起的非特征谐波

理想条件下忽略了晶闸管的换相过程，而实际中由于交流侧电感的影响，开关管的电流不能突变，换相过程不能瞬时完成[16]。因此，整流器的开关函数将不再是式(3)所示的方波形式。假设二次侧变压器漏感用集总电感LB表示，换相重叠角为γ。

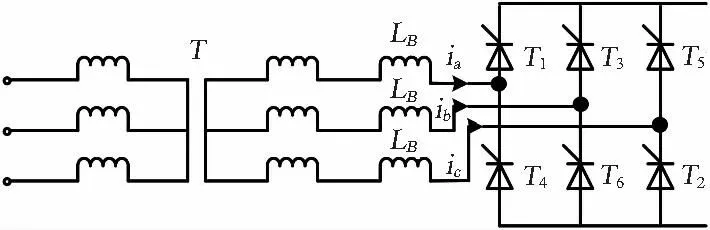
图2　变压器存在漏感时的Y-Y连接三相全波整流桥Fig.2　Three-phase full wave bridge rectifier while leakage inductance　exists in the Y-Y connection type transformers

根据对换相过程的分析可知，电压开关函数是有跃变的阶梯方波[4]，如图3所示。

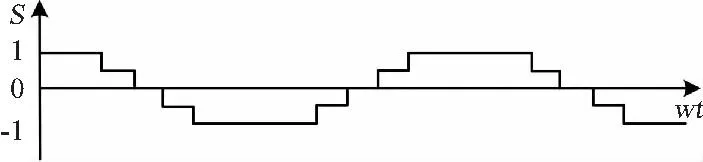
图3　考虑换相时的开关函数时域波形Fig.3　Expression of the switching function in time domain　considering the commutation

其傅里叶级数形式为：

(20)

式中：φ1为基波电压初始相位；α为晶闸管的触发角；γ为换相重叠角，且LB越大γ越大。

根据调制理论，换相过程中，直流侧输出电压为(T1和T3换相，T2导通)：

(21)

非换相过程时，直流侧输出电压为：

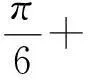
(22)

直流侧脉波的周期仍然是π/3，因此对其进行傅里叶级数展开可得VDC1，由于表达式中含有参数γ，结果十分复杂，此处不再列出，从结果可看出，Y-Y连接的三相全波整流器直流侧输出电压VDC1包含6n(n=1,2,3…)次谐波分量。假设2组变压器漏感相同，则Y-Δ连接的三相全波整流器直流侧输出电压与Y-Y连接时的输出电压之后π/6，经平衡电抗器后总的输出电压为两者的几何平均值，从结果分析得出考虑变压器漏感引起的换相时，12脉波整流输出直流电压包含6n(n=1,2,3…)次谐波分量(波形的对称性被破坏)，此分析结果对直流输出电流同样成立。又因换相期间输出电压降低，故而整流输出电压平均值也降低了。

3结果验证

根据图1所示的12脉波并联全桥整流器拓扑，在Matlab/Simulink中建立仿真模型，交流侧输入相电压有效值为220 V，频率为60 Hz，触发角为0°，负载电阻为0.25 Ω，负载电感为10 μH，开关器件采用晶闸管(其开通电阻为0.001 Ω，串联RC缓冲电路与之并联，其中缓冲电阻Rs=10-5，缓冲电容Cs=10-6)。分别对理想条件下和第2部分中所分析的几种非理想因素作用下的直流侧输出电流波形及其频谱进行验证。

图4为理想条件下12脉波整流直流侧输出电流波形及其频谱。

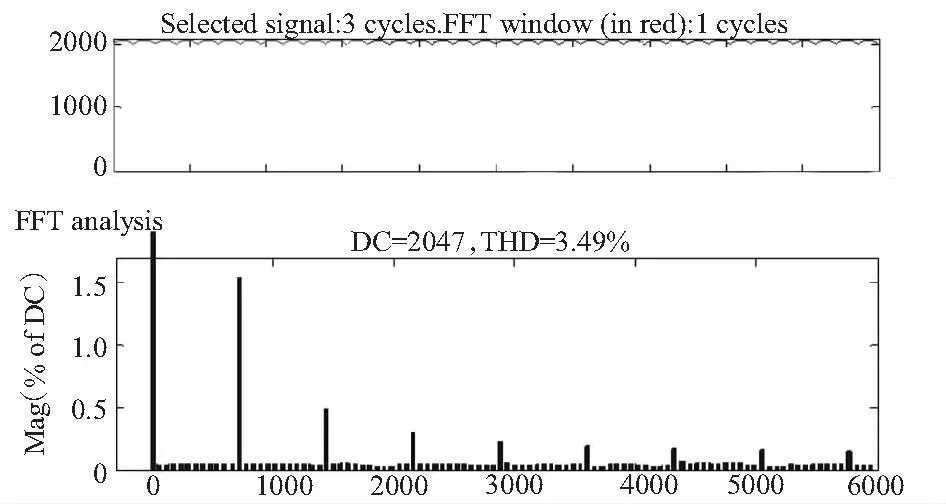
图4　理想条件下直流侧输出电流波形及其频谱Fig.4　Output DC current waveform and its spectrum under　ideal conditions

从图4可看出，输出直流电流是12脉动的，频谱中主要包含12n(n=1,2,3…)次谐波分量，且其幅值随次数增加衰减较快。由于仿真模型中变压器和晶闸管相关参数不完全理想，频谱中包含的其他各次谐波，但幅值均很小，可忽略不计。

图5为电网存在4%的负序分量且正负序相位差为0时的整流器直流侧输出电流及频谱。

图5中直流侧输出电流波形的周期为1/2×1/60 s，与第2部分分析相符，直流输出仍包含12n(n=1,2,3…)次谐波分量，但频谱中的2次谐波分量明显增加，其幅值仅次于直流分量。2次非特征谐波的引入会对直流用电设备和挂在在电网的滤波器带来很大的问题。

图6为第2组6脉波整流桥触发脉冲相位比第1组延迟2.16°时的整流器直流侧输出电流及频谱。

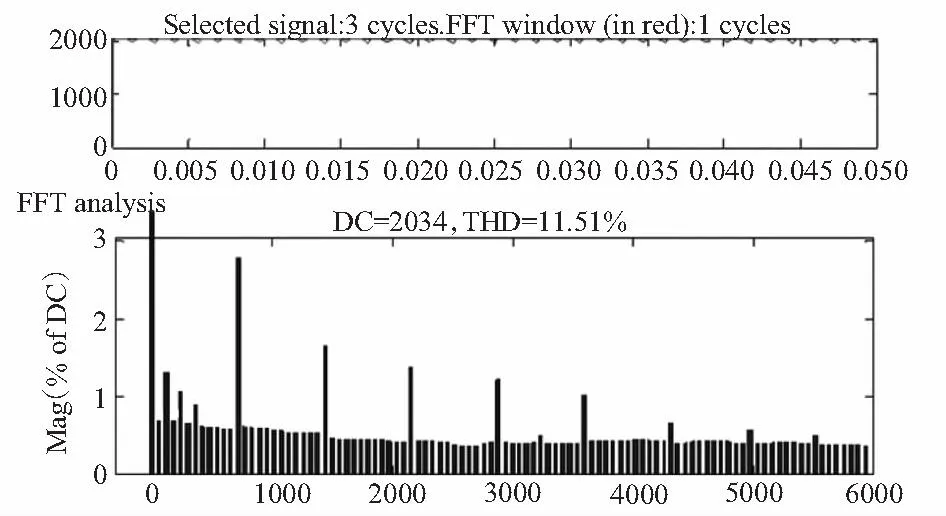
图6　触发脉冲间隔不对称时直流侧输出电流波形及其频谱Fig.6　Output DC current waveform and its spectrum while　the trigger pulse intervals are asymmetry

图6中直流侧输出电流波形的周期也是1/2×1/60 s，直流输出仍包含12n(n=1,2,3…)次谐波分量。与理想条件下的输出电流相比，频谱中的2n(n=1,2,3…)次谐波分量明显增加。与此同时，其他各次谐波分量及总的谐波畸变率均有明显增加。

图7为考虑变压器漏感引起的换相时的整流器直流侧输出电流及频谱(变压器漏感LB=10 μH)。

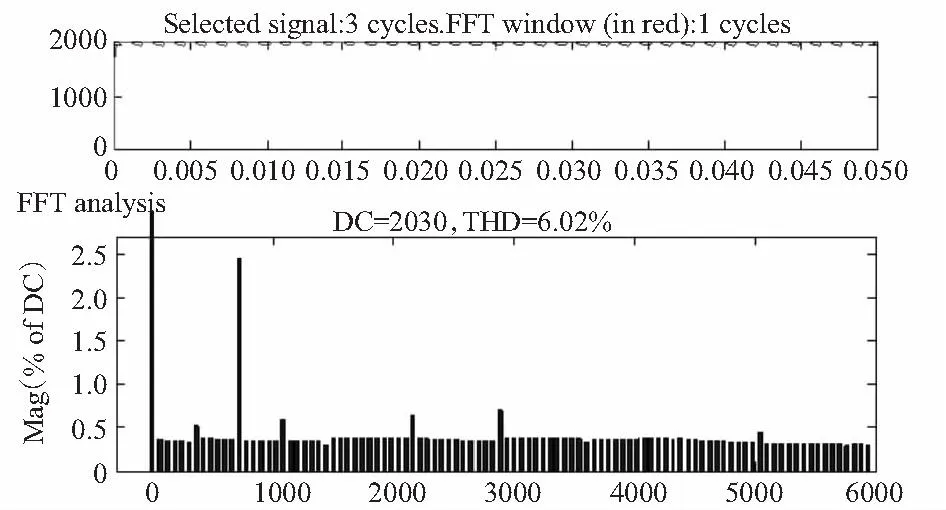
图7　考虑换相时直流侧输出电流波形及其频谱Fig.7　Output DC current waveform and its spectrum　considering the commutation

图7中直流侧输出电流波形的周期也是1/6×1/60 s，包含6n(n=1,2,3…)次谐波分量。但其他各次谐波分量均有明显增加，这是由开关器件的不理想引起的。

因此，第2部分理论分析计算与第3部分的Matlab/Simulink时域模型结果基本一致，说明理论计算的模型和方法可靠。

3结语

本文根据调制理论和傅里叶分析理论(开关函数法)对理想情况下和各种非理想情况下12脉波整流系统直流侧谐波特性进行了深入的分析，经过分析可得出如下结论：

1)理想12脉波整流系统直流侧包含12n(n=1,2,3…)次非特征谐波，谐波幅值随次数增加较快衰减。

2)当交流侧输入电压包含负序分量时，整流输出将出现2n(n=1,2,3…)次谐波分量，其中2次谐波幅值最大，危害也最大。

3)当触发脉冲间隔不对称时，直流侧输出也将出现低次非特征谐波。

4)当变压器存在漏电感时，输出波形会出现换相重叠角，且包含6n(n=1,2,3…)次谐波分量，并且系统总谐波畸变率也会增大。

总之，舰艇电网中整流系统实际运行时，会受到各方面因素的影响。不同运行状况下，其直流侧输出的谐波成分也会有很大差异。本文的分析方法可帮助我们理解整流系统谐波产生的机理，为有效地设计滤波装置提供参考。

参考文献：

[1]张志强,庄亚平,冀路明,等.舰船综合电力系统有源直流滤波器浅述[J].船电技术,2007(4):230-232,246.

ZHANG Zhi-qiang,ZHUANG Ya-ping,JI Lu-ming,et al.Review of active DC filter in shipboards integrated power system[J].Marine Electronic and Electronic Technology,2007(4):230-232,246.

[2]赵怀军,宋倩楠,邱宗明,等.舰船电力系统谐波的产生、危害和抑制[J].舰船科学技术,2007,29(4):61-65.

ZHAO Huai-jun,SONG Qian-nan,QIU Zong-ming,et al.Origination,harm and suppression of harmonics in ships electric power system[J].Ship Science and Technology,2007,29(4):61-65.

[3]HU Li-hua,YACAMINI R.Harmonic transfer through con-verters and HVDC links[J].Power Electronics, IEEE Transactions,1992(7):514-525.

[4]JOHN R,KRISHNAYYA P C S.Unusual current harmonics arising from high-voltage dc transmission[J].Power Apparatus and Systems, IEEE Transactions,1968(3):883-893.

[5]SUN Yuan-yuan,et al.A harmonically coupled admittance matrix model for AC/DC converters[J].Power Systems, IEEE Transactions,2007,22(4):1574-1582.

[6]孙媛媛,徐文远.整流器的谐波分析方法[J].电力自动化设备,2009(3):10-15.

SUN Yuan-yuan,XU Wen-yuan.Harmonic analysis method for converter[J].Electric Power Automation Equipment,2009(3):10-15.

[7]PHADKE A G,HARLOW J H.Generation of abnormal harmonics in high-voltage ac-dc power systems[J].Power Apparatus and Systems, IEEE Transactions,1968(3):873-883.

[8]孙媛媛,王小宇,尹志明,等.三相整流装置谐波产生机理分析及简化模型[J].电力系统自动化,2012,36(7):51-56.

[9]姜齐荣,赵东元,陈建业.有源电力滤波器[M].北京:科学出版社,2005.

[10]陈坚.电力电子学[M].北京:高等教育出版社,2002.

[11]YACAMINI R.Power system harmonics.Part 4: Interharmonics[C].Power Engineering Journal，1996:185-193.

[12]REEVE J O H N,BARON J A,KRISHNAYYA P C S.A general approach to harmonic current generation by HVDC converters[J].Power Apparatus and Systems, IEEE Transactions，1969(7):989-995.

[13]覃汉.大功率可控硅整流器的运行及其谐波分析[J].广西电力技术,2000(3):42-43+56.

[14]王磊,刘小宁,王伟利.大功率整流电路直流侧非特征谐波的分析[J].继电器,2007(3):37-40+65.

WANG Lei，LIU Xiao-ning，WANG Wen-li.Abnormal harmonic analysis of DC side in high power rectifying system[J].Relay,2007(3):37-40+65.

[15]游林儒,王炎,毕淑娥.可控整流器在非理想运行条件下的谐波分析[J].电力电子技术,2000(3):9-10+16.

YOU Lin-ru,WANG Yan,BI Shu-e.Harmonic analysis of rectifier under nonideal operating conditions[J].Power Electronics,2000(3):9-10+16.

[16]全恒立,刘志刚,张钢,等.地铁24脉波整流器空载直流侧谐波特性分析[J].铁道学报,2012(3):28-33.

QUAN Heng-li， LIU Zhi-gang， ZHANG Gang，et al. Research on DC floating voltage of 2 4 pulse phase′shifting rectifiers[J].Journal of the China Railway Society,2012(3):28-33.

Harmonic analysis of 12-pulse rectifier for ship at the DC side

QIN Meng-tao,SONG Wen-wu,HUANG Cheng

(Science and Technology on Electromagnetic Compatibility Laboratory,Wuhan 430064,China)

Abstract：For harmonic problems of modern warships DC grid, the operation principle and characteristic harmonics at the DC side under ideal conditions of the 12-pulse wave parallel full bridge rectifier are analyzed. On basis of that, the harmonic conditions are calculated and analyzed using modulation theory and Fourier analysis and simulated using Matlab/Simulink when the AC side voltage is asymmetry, the trigger pulse intervals are asymmetry and considering the commutation caused by the transformers′ leakage inductance. The results indicate that the 2th and 4th harmonic components increase obviously when the AC side voltage is asymmetry and the trigger pulse intervals are asymmetry of the 12-pulse wave rectifier. Also，when considering the commutation, the output current consists of 6 nth harmonics and the whole harmonic distortion increases significantly.

Key words：non-characteristic harmonics; 12-pulse wave rectifier; switching function; fourier analysis

作者简介：秦萌涛( 1990 - ) ，男，硕士研究生，主要研究方向为舰船电磁兼容及有源电力滤波器。

收稿日期：2014-04-18； 修回日期： 2014-05-08

文章编号：1672-7649(2015)02-0101-06

doi：10.3404/j.issn.1672-7649.2015.02.021

中图分类号：TM48

文献标识码：A