一类具分段常数变量的捕食-食饵系统的Neimark-Sacker分支
陈斯养,靳 宝
陕西师范大学, 数学与信息科学学院, 西安 710062
一类具分段常数变量的捕食-食饵系统的Neimark-Sacker分支
陈斯养*,靳 宝
陕西师范大学, 数学与信息科学学院, 西安 710062
讨论了具时滞与分段常数变量的捕食-食饵生态模型的稳定性及Neimark-Sacker分支;通过计算得到连续模型对应的差分模型,基于特征值理论和Schur-Cohn判据得到正平衡态局部渐进稳定的充分条件;以食饵的内禀增长率为分支参数,运用分支理论和中心流形定理分析了Neimark-Sacker 分支的存在性与稳定性条件;通过举例和数值模拟验证了理论的正确性。
分段常数变量;时滞;稳定性;Neimark-Sacker分支
种群生态学是迄今数学在生态学中应用最为广泛、发展最为成熟的生态学的分支。捕食-食饵系统是种群生态学中生物种群相互之间的基本关系之一,是构成复杂食物链、食物网和生物化学网络结构的基石,从而引起了广大数学工作者和生物学家的关注。祁君和苏志勇[1]在经典的捕食-食饵系统中考虑到由于捕食效应对食饵种群带来的正向调节作用后,提出了具有捕食正效应的捕食-食饵系统。从理论上说明了正向调节作用对系统的影响,并就第一象限内平衡点存在时的相图解释了捕食正效应的作用。杨立和李维德[2]利用概率元胞自动机模型对空间隐式的、食饵具Allee 效应的一类捕食-食饵模型进行模拟,发现随着相关参数的变化,种群的空间扩散前沿由连续的扩散波逐渐转变为一种相互隔离的斑块向外扩散。Freedman 与 Wolkowicz 在Rosenzweig-MacArthur模型[3]中选取第4功能反应函数进行了全局范围内的分支情况的研究。经典的捕食-食饵模型可以被表达成如下的非线性微分方程模型:
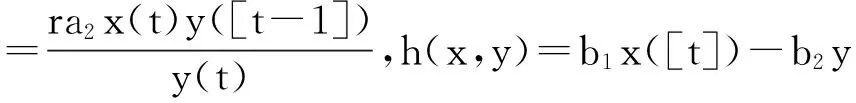
(1)
模型(1)满足初始条件:
x(0)=x0>0y(s)=φ(s)≥0,φ(0)>0,φ∈C([-1,0],R+)
(2)
式中,r表示食饵的内禀增长率,a1表示食饵的环境容纳量,a2表示捕食系数,b1表示捕食效率常数,[t]表示对变量t∈[0,+)取整。
1 正平衡态稳定性分析
由模型(1)可知b1>a1s时,模型(1)存在惟一的正平衡态:
定理1 模型(1)满足初始条件(2)的解为正、全局存在且有界(∀t≥0)。
说明:对定理1运用反证法和比较原理即可得证,故将其证明略去。
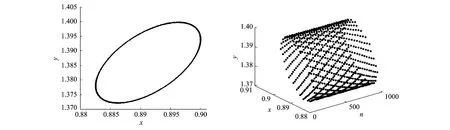
当n≤t (3) 对(3)由n到t积分并令t→n+1,即得: (4) 得(4)式的线性近似系统 υ(n+1)=Aυ(n)+Bυ(n-1) (5) 其中 υ(n)=(ψ(n),φ(n))T 则线性系统(5)的特征方程为 λ3+ϑ1λ2+ϑ2λ+ϑ3=0 (6) 其中 以下应用Schur-Cohn判据[13]对模型(1)正平衡态稳定性进行分析,给出捕食者和食饵共存且数量保持稳定的条件。 定理2模型(1)满足下列5种情况之一: (2)当M3=1时,P5 (5)当M3<1,M5>0,Δ>0时,P1 其中: 最后考虑条件(Η3) 由ϑ1<0,ϑ2>0,ϑ3>0知(Η2)和(Η3)⇔(M32-M3)P2+M4P+M5<0等价于如下条件(v)或(vi): (v) 当M3>1时,知M5>0,若Δ<0或Δ>0,M4>0(此时Pi<0(i=1,2)),则其交集为空集;若Δ>0,M4<0,知 Pi>0(i=1,2),P1 (vii) 当M3<1时,知M32-M3<0,若Δ<0时,0 由此知0 本节以r作为分支参数,分别讨论模型(1)的Neimark-sacker分支存在性及其分支方向与稳定性。因情况(2)不会产生分支(分支临界值r0趋于零或无穷大),故下文对定理2中(1)的情况给出产生分支的条件,情况(3)的分支条件可同理给出。 下面讨论模型(1)的分支方向及其稳定性. 将(4)式写作如下变换形式: (7) 取 B(x,y)和C(x,y,z)分量分别为: 还有一种情况就是动静互衬,也就是既描写运动的事物又描写静止的事物,使一方衬托另一方,特点更为突出。如: 记 z7=F1,x1x1x1,z8=F1,x1x1x3=F1,x1x3x1=F1,x3x1x1z9=F1,x3x3x1=F1,x3x1x3=F1,x1x3x3, z10=F1,x3x3x3,z11=F2,x3x3x3,z12=F2,x1x1x2=F2,x1x2x1=F2,x2x1x1,z13=F2,x2x2x1=F2,x2x1x2=F2,x1x2x2,z14=F2,x2x2x2 经计算可知: (8) (9) 其中: 经计算: 其中: 经计算可知: 由以上计算知ζ的表达式如下: 由如上分析和推理可得如下定理4。 本节将通过实例,运用Matlab软件绘出相应的分支图,验证以上理论的可行性,并通过图形说明该模型复杂的动力学行为。 例 在模型(1)中,取a1=0.5,a2=0.4,b1=4,b2=2.5,s=0.1计算可得: M3=1.2400,M4=-1.8426,Δ=2.7092,ζ=-0.4851<0,Ρ1=0.3304>(M3-1)/M3=0.1935 则分支参数的临界值r0=2.4852,惟一正平衡态E(0.8912,1.3860) 对应分支图为图1。由图1可知,当r 图1 r-x,r-y分支图Fig.1 r-x,r-ybifurcation map 图2 x,y稳定解图(r=2.26 图3 稳定图(r=2.26 图4 N-S分支图Fig.4 N-S bifurcation map 图5 x,y像平面图和空间解图(r=r0=2.4852)Fig.5 phase plane and space solution map of x and y (r=r0=2.4852) 本文应用Schur-Cohn判据、分支理论及中心流形投影等理论给出了具有时滞与分段常数变量捕食-食饵模型的稳定性及Neimark-sacker分支的存在性以及稳定性条件。通过模型的分析得到如下两个主要结论: H1) 在捕食-食饵系统中考虑捕食者只在一定时间段或整数时刻且具有滞后效应捕食时,由定理2可知,系统的稳定性(捕食者和食饵共存且数量保持稳定)将会变得非常复杂。 H2) 由实例可知,系统在其它参数不变的情况下,当食饵的内禀增长率r<2.4852时,由图1—图3可知捕食者和食饵的数量处于稳定状态;当r=2.4852,由图4,图5知捕食者和食饵的数量将呈现周期性变化,系统产生Neimark-sacker分支;当r>2.4852时,由图1知系统的正平衡态由稳定到不稳定。 综上所述,在捕食-食饵系统中,若考虑捕食者只在一定时间段或整数时刻且具有滞后效应捕食时,模型动力学行为将变得更为错综复杂;食饵的内禀增长率达到确定的临界值时,种群数量将失去原有的稳定性,模型将产生惟一稳定的超临界Neimark-Sacker分支。 [1] 祁君, 苏志勇. 具有捕食正效应的捕食-食饵系统. 生态学报, 2011, 31(24): 7471- 7478. [2] 杨立, 李维德. 利用元胞自动机研究一类捕食食饵模型中的斑块扩散现象. 生态学报, 2012, 32(6): 1773- 1782. [3] Kot M. Elements of Mathematical Ecology. London: The Cambridge University Press, 2001: 107- 160. [4] He Z M, Lai X. Bifurcation and chaotic behavior of a discrete-time predator-prey system. Nonlinear Analysis: Real world Applications, 2011, 12(1): 403- 417. [5] Wang W M, Ling L. Stability and Hopf bifurcation analysis of a delayed predator-prey model with constant rate harvesting. Journal of Mathematical Biology, 2009, 24(4): 1- 14. [6] Wang J F, Shi J P, Wei J J. Predator-prey system with strong Allee effect in prey. Journal of Mathematical Biology, 2011, 62(3): 291- 331. [7] Beretta E, Kuang Y. Global analyses in some delayed ratio-dependent predator-prey systems. Nonlinear Analysis: Theory, Methods & Applications, 1988, 32(3): 381- 408. [8] Skalski G T, Gilliam J F. Functional responses with predator interference: viable alternatives to the Holling type II model. Ecology, 2001, 82(11): 3083- 3092. [9] Mischaikow K, Wolkowicz G. A predator-prey system involving group defense: a connection matrix approach. Nonlinear Analysis: Theory, Methods & Applications, 1990, 14(11): 955- 969. [10] Jost C, Arditi R. From pattern to process: identifying predator-prey models from time-series data. Population Ecology, 2001, 43(3): 229- 243. [11] Salt G W. Predator and prey densities as controls of the rate of capture by the predatorDidiniumnasutum. Ecology, 1974, 55(2): 434- 439. [12] Martin A, Ruan S G. Predator-prey models with delay and prey harvesting. Journal of Mathematical Biology, 2001, 43(3): 247- 267. [13] Jury E I. Theory and Application of the Z-transform Method. New York: Wiley, 1964. [14] Kuznetsov Y A. Elements of Applied Bifurcation Theory. New York: Springer-Verlag, 2004. Neimark-Sacker bifurcation behavior of predator-prey system with piecewise constant arguments CHEN Siyang*, JIN Bao CollegeofMathematicsandInformationScience,ShaanxiNormalUniversity,Xi′an710062,China The dynamic relationship between prey and predator has long been and will continue to be a dominant theme in ecology because of its universality. The prey-predator interaction, one of the most fundamental interspecies interactions, was first described mathematically by Lotka and Volterra in two independent works, resulting in what are now called the Lotka-Volterra equations. A predator-prey model based on the logistic equation was initially proposed by Alfred J. Lotka in 1910 to describe autocatalytic reactions. He later developed this model and in 1925 arrived at the Lotka-Volterra equations that we know today. Almost at the same time (1926), Vito Volterra, an Italian mathematician, independently established the Lotka-Volterra model after analyzing statistical data of fish catches in the Adriatic. The Lotka-Volterra equation is one of the fundamental population models in theoretical biology. Since these early works, prey-predator interactions have been studied systematically. Much of this work has focused on models with continuous time delay as well as their stability, oscillations, Hopf bifurcations and limit cycles, but no attention has been paid to models with piecewise constant arguments and a time delay. In fact, because of environmental factors or predator characteristics, prey are often captured only during certain times of the season. In addition, there is a time delay before hunting because of predator maturation times in practical predator-prey systems. Therefore, it is more realistic to employ the functional response with piecewise constant arguments and a time delay in predator-prey models. In this paper, we discuss the stability and bifurcations of predator-prey systems with piecewise constant arguments and a time delay. First, a discrete model that can equivalently describe the dynamical behavior of the original differential model is deduced. Sufficient conditions for the local asymptotic stability of the steady state are achieved based on an analysis of the eigenvalues and Schur-Cohn criterion. Second, by choosing a parameter r, the intrinsic growth rate of prey, as the bifurcation parameter and using the bifurcation theory and center manifold, we find that the discrete model undergoes a Neimark-Sacker bifurcation at an exceptive value ofr. The results show that 1) the stability of the predator-prey system is very complex when we consider piecewise constant arguments and a time delay; and 2) the positive equilibrium of the model switches from being stable to unstable as the intrinsic growth rate of prey increases beyond a critical value, at which point the unique supercritical Neimark-Sacker bifurcation will occur. Finally, computer simulations based on the system supported our main results and illustrated them intuitively. The numerical examples also justify the reasonableness of the conditions given in our paper for the loss of equilibrium. The parameters of the predator-prey model come from nature. However, we can still add to the model a feedback control factor and interference from outside to change the equilibrium, bifurcation point, or amplitude of the periodic solution. Study of our model and its ameliorated version can provide a theoretical basis for understanding ecology and protecting the environment. piecewise constant arguments; delay; stability;Neimark-Sacker bifurcation 国家自然科学基金资助项目(11171199, 61273311); 中央高校基本科研专项基金资助项目(GK201302004, GK201302006) 2013- 06- 05; 日期:2014- 05- 08 10.5846/stxb201306051340 *通讯作者Corresponding author.E-mail: chsy398@126.com 陈斯养,靳宝.一类具分段常数变量的捕食-食饵系统的Neimark-Sacker分支.生态学报,2015,35(7):2339- 2348. Chen S Y, Jin B.Neimark-Sacker bifurcation behavior of predator-prey system with piecewise constant arguments.Acta Ecologica Sinica,2015,35(7):2339- 2348.



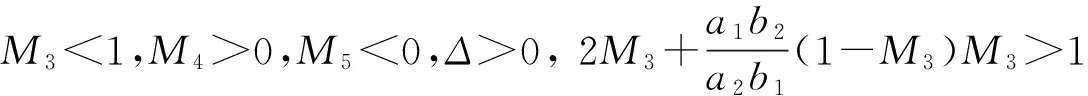

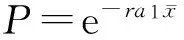
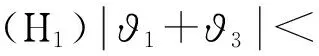

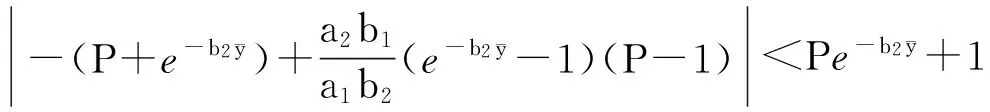
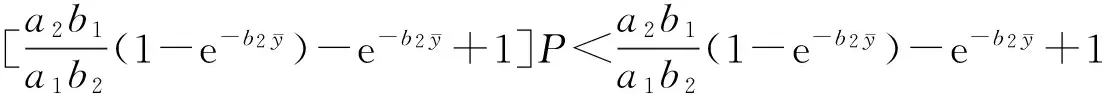


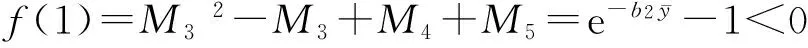



2 Neimark-Sacker分支分析



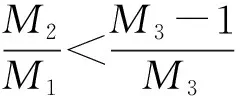
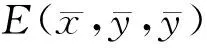


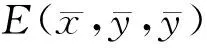



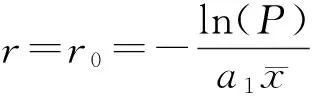
3 数值计算




4 总结

