离心风机工况点改变时的转数计算

张立奎

（深圳市百斯特环保工程有限公司，广东深圳518055）

在化工、冶金、环境工程废气治理及通风工程设计和运行中，都会面临离心风机（以下简称风机）在管网中工况点的确定及其改变时风机转数相应的调整问题。管网中风机工况点为风机性能曲线和管网性能曲线交点。管网中风量、风阻变化或两者同发生变化，工况点都会发生变动，当风机满足不了需求时，风机的转数应随之进行相应调整才行。新的工况参数：风量、风压下的风机转数如何求取，在一些工程技术人员中不很清楚，常常出现概念上混乱，导致不该有的失误。本文将对这一问题详细阐述。

1 风机和管网的性能曲线

1.1 风机性能曲线

风机的风压与风量pt-Q、内功率与风量Ni-Q及内效率与风量ηi-Q 关系曲线称风机的性能曲线。这3 条曲线均由实验测出，至今还无法用数学解析式表示。在工况点及转数计算中用的最多的是pt-Qt线，其次Ni-Q 线。当转数增大时，pt-Q 曲线及Ni-Q 曲线均上移；反之，均下移。具体绘制是在原转数n1的pt-Q 或Ni-Q 线上取若干点参数值（Q，pt）或（Q,Ni）,代入风机的比例定律算式（见下文）求出新转数n2的相对应各点值，再绘成曲线。

1.2 管网性能曲线

管网中风阻与风量pf-Q 关系线称管网性能曲线，该曲线方程可由流体流动的柏努利（Bernoulli）方程导出；Pf=ΔZ·ρ·g+ΔPc+KQ2

式中 Pf：管网总风阻，Pa，其值等于管网风机的风压，Pf=Pt；ΔZ：气流进、出管网位差，m；ρ：气流密度，kg·m-3；g：重力加速度，9.81m·s-2；ΔZ·ρ·g：位压差，Pa，在计算涉及的高度范围内若不考虑大气压变化时，则不计位压差，ΔZ·ρ·g=0；ΔPc：气流进、出管网静压差，Pa；Q：风量，m3·s-1或m3·h-1；K：表征管网的性能，称管网性能系数，K 包含管网中各种与流量有关的摩擦因数及阻力系数。对一定管网（指管网系统、管内径、管长度、网中阀门开启度、管网中的设备、风道中障碍物等均不变），K 近似为一常数。K 有因次，为Pa·m-6s2或Pa·m-6h2,其数值和因次随风量、风阻、气流密度、流通面积等所采用因次不同而不同。管网内风阻越大，K 值越大。

当忽略了位压差后，则上式：Pf=ΔPc+KQ2（1）式（1）反映管网内风量与风阻关系，称管网性能曲线方程，为一个二次抛物线方程，ΔPc为抛物线截距。K 值越大抛物线越陡峭，则输送同样气量风机需提供的风压（能量）越大，反之，需提供风压越小。

当管网进出端口都与大气相通时，则Δpc=0,式（1）为：

式（2）为一通过坐标原点的二次抛物线方程，也是最常见的管网性能曲线方程，常称之狭义管网性能曲线方程，其绘制的曲线为狭义管网性能曲线，而式（1）绘制的曲线则常称广义管网性能曲线。在无特指情况下，一般说的风机管网性能曲线方程均指式（2）。

2 比例定律及等效率线方程

风机比例定律是由相似理论得出的。对于两相似风机，不但要几何形状相似（主要叶轮形状相似），且机壳内气流受力（主要粘滞力，惯性力，静压力）方向相同，大小成比例，满足这两条件，气流在机壳内流动工况相似，因此它们内效率是相等的。这样便可导出风机相似定律算式（5）：

式中 D：叶轮外径，m；ρ：输送气体密度，kg·m-3；Kp：气体压缩系数，当风机风压Pt≤2500Pa 时，可不计Kp的影响；当风机风压Pt＞2500Pa,需计入Kp值；下标“M”的为模型风机。

式中 γ：绝热压缩指数，对空气，γ=1.4；Pt：风机风压（全压），Pa；P1：风机进口气流压力，Pa。

对于同一风机或同一型号风机，当输送同一状态气体、风压Pt≤2500Pa 时，若转数不同，则式（Ⅰ）简化为

这就是常用的风机比例定律算式。要注意的是式（Ⅱ）中的“1、2”两点是同一型号两相似体内或同一风机体内流动工况相似的两工况点。

由比例定律算式：

故

式（3）为一个通过坐标原点二次抛物线方程，在该抛物线上各点流动工况相似、内效率是相等的，称（风压）等效率线方程。kp称风压等效率系数。

比较式（2）和式（3）：因Pf=Pt，故K=kp，式（2）、（3）两式重合，即狭义管网曲线方程与风压等效率方程相重合。

用同样方法由比例定律也可得：

故

式（4）为一个通过坐标原点的3 次抛物线方程，在该抛物线上各点流动工况相似、内效率是相等的，称（功率）等效率线方程。kN称功率等效率系数。

3 工况点改变时的风机转数计算

3.1 管网性能曲线不变，工况点沿管网线上移

生产上由于某种原因，要求在原有的管网内改变（如增大）风量，就属于这种情况。当管网一定，风量增大，风阻也随之增加，因此，需增大风机的转数，使风压提高，才能克服风阻满足需求。

3.1.1 狭义管网性能曲线方程

如图1，工况点由A1变到A2。此时由于K=kp管网性能曲线与风压等效率曲线重叠，A1、A2两点为等效率工况点。只要将A1、A2的相关参数值代入比例定律算式即可求出n2：

图1 A1 沿管网线变Fig.1 A1 moving along the curve of duct system

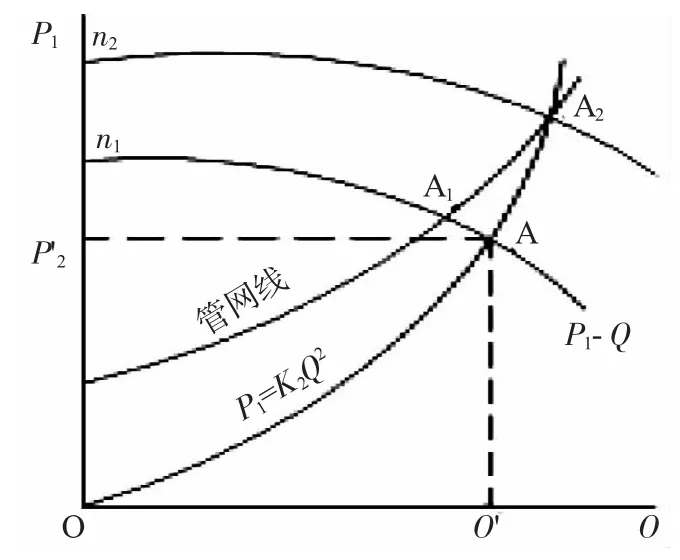
图2 A2 沿广义管网线变Fig.2 A1 moving along the curve of broad meaning duct system

3.1.2 广义管网性能曲线方程

此时需将改变后的工况点A2参数值（Pt2，Q2）代入式（3）风压等效率曲线方程中，则

在风机性能曲线及管网性能曲线图上（图2），绘出此风压等效率曲线，该曲线通过A2点并与n1转数的风机Pt-Q 性能曲线交于A' 点（Q'，Pt'），则A'与A2均为等效率曲线上的点，可用比率定律进行计算n2：

3.2 管网性能曲线改变，工况点沿等流量线移动

管网内由于某种原因风阻改变（如增加）而生产上又要保持原有的风量属于这种情况，此时工况点沿Q1垂线移动。

变动后的工况点为A2，A2在Q1垂线上。将A2点参数风量Q1、风压Pt2值代入式（3），求出风压等效率性能曲线方程：

若管网曲线是狭义管网性能曲线，因kp=K 故Pt=KQ2因此，这也是新的狭义管网性能曲线方程。在原风机性能曲线和管网性能曲线图上绘制风压等效率曲线。该曲线通过A2点并与n1风机Pt-Q 性能曲线交于A' 点（Q'，Pt'）（图3，图4）。A' 点与A2点均在风压等效率线上:

图3 A1 不沿管网线变Fig.3 A1 moving along the Q1 perpendicular line（for the curve of duct system

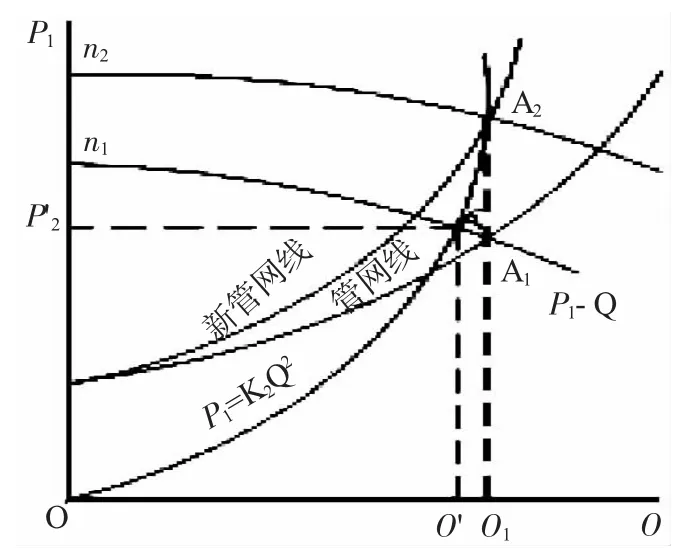
图4 A1 不沿广义管网线变Fig.4 A1 moving along Q1 perpendicular line line（for the curve of duct system（for the curve of broad meaning duct system）

例1.某离心风机，型号4-72No.20B,630r·min-1,在管网中运行的工况点A1参数Q1=56.7m3·s-1,Pt1=1800Pa，管网性能曲线方程Pt=0.56Q（2图5）。现因生产需要，在管网中增添新的设施，管网的风阻将增至2620Pa。如欲维持原风量，问此时风机的转数应调整为多少？已知风机进气压力100kPa。

解：风阻增加后，工况点由A1变为A（256.7m3·s-1,2620Pa）（图5）：

由风压等效率曲线方程：

因为管网曲线为狭义管网性能曲线，故上式也是风阻变化后新的管网性能曲线方程。将此式绘成曲线，该曲线通过A2点并与n1（630r·min-1）转数风机Pt-Q 性能曲线交于A' 点（Q'=50.6m3·s-1,Pt'=2090Pa）（图5）。风机转数调至：

因P2=2620Pa＞2500Pa,需计算气体压缩系数影响，由式（Ⅰ-1）

同样方法可得A' 点风压2090Pa 系数KP'=0.993，=0.998≈1

故可不计气体压缩系数对风压等效率曲线方程影响。

图5 沿Q1 线移动n2 的计算2（管网性能曲线）Fig.5 Calculating n2 during A1 moving along Q1 perpendicular line（for the curve of duct system）

图6 A1 沿Q1 垂线移动的计算（广义管网性能曲线）Fig.6 calculating n2 during A1 moving along Q1 perpendicular line（for the curve of broad meaning duct system）

例2.如上例管网出口端通入静压300Pa 某一设备，则管网性能曲线为：Pt=300+0.56Q2,原工况点A1:Q1=53.7m3·s-1，Pt1=1915Pa.欲维持原风量不变，则管网中风阻需增至2410Pa，问此时风机的转数应调至多少才行？

解：新工况点A2（Q2=53.7m3·s-1，Pt2=2410Pa），求风压等效率曲线方程：

绘制此风压等效率方程曲线（图6），该曲线通过A2点并交n1转数（630r·min-1）风机Pt-Q 性能曲线于A'点（Q'=50.3m3·s-1,Pt'=2115Pa）（图6）。故风机转数应调至：

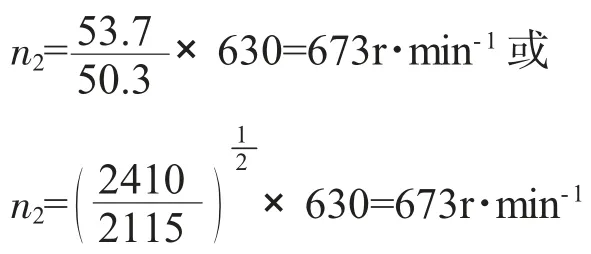
若本题欲求新管网性能曲线，只需将原管网曲线抛物线截距及A2工况点风压Pt2、风量Q1值代入式（1）即可求出管网曲线性能系数K：

图6 中未绘出新的管网性能曲线。

4 功率等效率曲线应用

工况点改变时风机转数计算也可用功率等效率曲线，但比较麻烦，尤其是对广义管网性能曲线。

4.1 工况点沿管网性能曲线移动

在管网和风机Pt-Q 性能曲线图上，再绘出风机Ni-Q 功率性能曲线。

4.1.1 狭义管网性能曲线

在图7 上，Q1垂线与Ni-Q 线交于A1N点（Q1,Ni1），将其参数值代入式（4）得

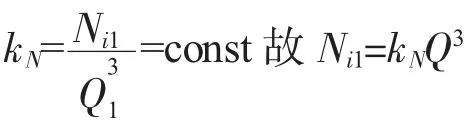
绘制此功率等效率方程曲线，该曲线通过A1N点与Q2垂线相交于A2N（Q2,Ni2）,则A2N与A1N在功率等效率线上，故

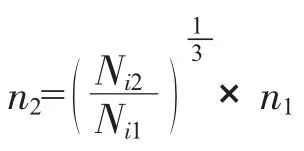
4.1.2 广义管网性能曲线

在图8 上，绘制出通过A2点的风压等效率曲线=const，故得Pt=kpQ2，该线与n1转数风机Pt-Q 的性能曲线交于A' 点（Q',Pt'）,Q' 垂线与n1时的Ni-Q 风量功率性能曲线交于AN' 点（Q',Ni'），将Q'Ni" 值代入式（4）得=const，于是得功率等效率曲线方程：Ni=kNQ3。在图8 上绘出该曲线，该曲线通过AN'点并与Q2垂线交于A2N（Q2，Ni2）,AN'与A2N在功率等效率线上，则：

图7 A1 沿管网线变及Ni-Q3 线Fig.7 A1 moving along the curve of duct system and Ni-Q3 curve

图8 A1 沿广义管网线变及Ni-Q3 线Fig.8 A1 moving along the curve of broad meaning duct system and Ni-Q3 curve

4.2 管网性能曲线改变，工况点沿等流量线移动

在图9、10 上（此两幅图上均未绘出原和新管网性能曲线），工况点由A1移至A2。将新工况点A2（Q1，Pt2）值代入式（3）得风压等效率曲线方程。若是狭义管网曲线，因kp=K，故该方程也即狭义管网曲线方程：

此曲线与n1转数风机的性能曲线Pt-Q 交于A'点（Q'Pt'），作Q'垂线，与n1转数Q-Ni风机性能曲线交于AN′点（Q'，Ni′），将此参数值代入式（4）得功率等效率曲线方程：

在同一图上，绘出此功率等效率曲线，该曲线通过AN' 点并与Q1线交于A2N点（Q1，Ni2）（图9，图10），AN'点与A2N均在功率等效率线上

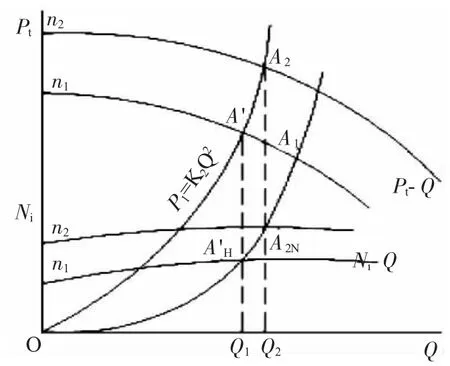
图9 A1 不沿管网线变及Ni-Q3 线Fig.9 A1 moving along Q1 perpendicuar line（for the curve of duct system）and Ni-Q3 curve

图10 A1 不沿广义管网线变及Ni-Q3 线Fig.10 A1 moving along Q1 perpendicular line（for the curve of broad meaning duct curve）and Ni-Q3 curve

5 结语

5.1 求解n2 关键——等效率线方程

综上所述可见：当管网工况点改变时，求解n2关键是由改变后的工况点A2坐标参数求出（风压）等效率曲线方程。将该方程绘成曲线，曲线通过A2点，并与n1转数风机Pt-Q 性能曲线相交得出A'点。因A'与A2为等效率点，故将坐标参数代入比例定律即可求得n2。若是狭义管网性能曲线，因这种情况（风压）等效率曲线与管网性能曲线一致，所以当工况点沿管网性能曲线变动时就不需再求出（风压）等效率曲线方程了，可直接用管网性能曲线。用功率等效率曲线求解工况点变动时的风机n2十份烦冗，且计算完全是多余的，如图7～9 及图10 之情况：因为风压等效率曲线及相关的等效率点已经得出，用比例定律就已经可算出n2，再继续往下算功率等效率曲线就多此一举了。因此，使用功率等效率曲线求n2仅仅只有理论上意义，唯一好处是可加深我们对风机各性能曲线理解及明确这样一个概念：求n2关键是必须确定等效率工况点，为此先要求出等效率曲线方程绘制出等效率曲线。

5.2 关于风机比例定律

比例定律使用先决条件是指两几何相似风机在流动工况相似条件下得出的，即使是对于同一风机，但在转数改变时，要做到流动工况完全相似依然是困难的，因此用比例定律进行计算时存在一定的近似性，转数相差愈大，则近似性愈大，一般转数变化控制在15%～20%之内。

5.3 输液管网相关计算

比例定律同样适用于输液管网，离心泵壳内相似工况点，其比例定律形式为：

式中 H：泵的压头，m；N：泵轴功率，kW；η：离心泵效率。

对于输液管网，其性能曲线多为广义管网性能

曲线，类似于式（1）：

Hf=HC+KQ2

式中 HC=△Z+为位头与静压头和,m 在极特殊情况下（罕见）：HC=0,则输液管网性能曲线为：Hf=KQ2此式类似风管管网狭义性能曲线，即式（2）。

同样，对离心泵，其等效率曲线方程有：

压头等效率曲线方程：

H=KNQ2式中kH=const.

率等效率曲线方程

N=KNQ3。式中kN=const.

当工况点变动时，进行转数等相关计算，其方法类似风机管网中的计算，本文不再赘述。

［1］谭天恩，窦梅.化工原理（上册）［M］.北京：化学工业出版社，2014.61-65.

［2］王志魁，化工原理［M］.北京：化学工业出版社，2004.67-71；80-81.

［3］张玉成，仪登利.通风设计与选型［M］.北京：化学工业出版社，2011.95-97.

［4］商景泰.通风机实用技术手册［M］.北京：机械工业出版社，2011.

［5］张立奎.离心风机无因次性能曲线［J］.南昌大学学报（工科版），2013，（3）.

［6］张立奎.离心风机在选择和变工况点时性能参数换算［J］.化工装备技术,1996，（4）.

［7］孙研.风机产品样本（上、下册）［M］.北京：机械工业出版社，2003.