C*代数斜多项式构成的完备化空间

陈本菊

(重庆师范大学数学学院,重庆 401331)

C*代数斜多项式构成的完备化空间

陈本菊

(重庆师范大学数学学院,重庆 401331)

C*代数里的元素构成的多项式代数是不完备的,利用补充极限点使之完备化,即成为一个巴拿赫空间,文中证明了斜多项式代数的完备化空间构成一个巴拿赫代数,且也是一个C*代数.

C*代数;多项式代数;完备化;等距同构

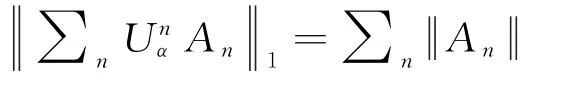
令l1(,α)为P(,α)在这个范数下的完备化空间.若l1(,α)是C*代数.则l1(,α)的二次对偶l1(,α)**也可以以一种自然的方式看作一个冯·诺依曼代数.

1 准备知识

定义1[5-6]设(,ρ)是度量空间,{xn}是中的点列,如果对于任一正数ε,存在正数N(ε),使得当自然数n,m≥N(ε)时ρ(xn,xm)＜ε,就称{xn}是中基本点列,或称为Cauchy点列.如果度量空间中每个基本点列都收敛,就称是完备度量空间.完备的赋范线性空间又称为巴拿赫空间(Banach space).

定义2是度量空间,A及E是中点集,如果E中任何一点x的任何环境中都含有集A中的点,就称A在E中稠密.如果有完备的度量空间,使得保距同构于的稠密子空间,则称1是的完备化空间.

定理1 (1)A在E中稠密的充要条件是⊃E.

(2)A在E中稠密的充要条件是对任一x∈E,有A中的点列{xn},使得xn→x(n→∞).

定理2 对于任一度量空间必存在完备化空间.

定理3 设,是度量空间的两个完备化空间,则必有→的等距同构映照φ,使得对一切x∈,φ(x)=x.因此,度量空间的完备化空间在等距同构的意义下是唯一的.

证设1,2是度量空间的两个完备化空间,则在1中稠密,对于每个ξ∈,必有一列{xn} ⊂,使得在中{xn}→ξ.{xn}同时是中的基本点列,则必存在x′∈,使得在中{xn} →x′,我们作映射

φ为等距同构映射.

定义3[1]若是一个复巴拿赫空间,在上定义了一个乘法运算满足条件:

2 C*代数斜多项式构成的完备化空间

定义4[2]令为C*代数,α是上的自同态.斜多项式代数P(,α)由所有形如的多项式构成,其中An∈,变量Uα满足A Uα=Uαα(A).

命题1 上式定义的范数的确满足范数的三条性质.

证为不引起混淆,范数统一用表示.设P∈P(,α),则

令l1(,α)为P(,α)在这个范数下的完备化.

定理4是巴拿赫空间.

证设为中一列基本点列,n=1,2,3,….则∃N＞0,当n,k＞N时,对∀ε＞0,都有

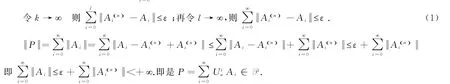
是巴拿赫空间.

命题2 P(,α)在中稠密.

证设

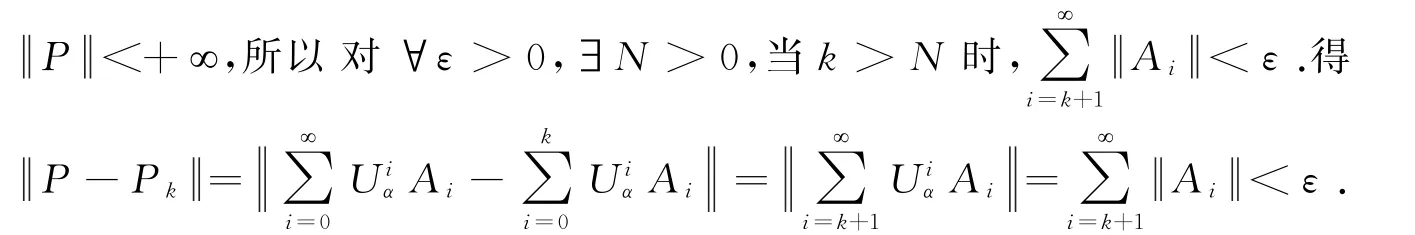
3 结论

l1(,α)为P(,α)在这个范数下的完备化空间.由定理3,度量空间的完备化空间在等距同构的意义下是唯一的.

定理5 l1(,α)等距同构于.

证l1(,α)为P(,α)的完备化空间,∃P′∈l1(,α),使得Pn→P′(n→∞),Pn∈P(,α).作映照

ψ(P)=P′

ψ(x y)=ψ(x)ψ(y),

由收敛序列极限的唯一性知ψ为双射.

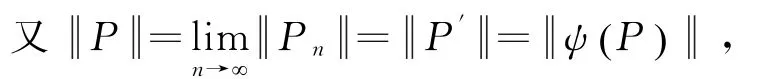
ψ为等距同构映照.因此l1(,α)等距同构于.

因此l1(,α)与在等距同构的意义下看作是一样的,即l1(,α)=.

定理6 l1(,α)是巴拿赫代数.

证设

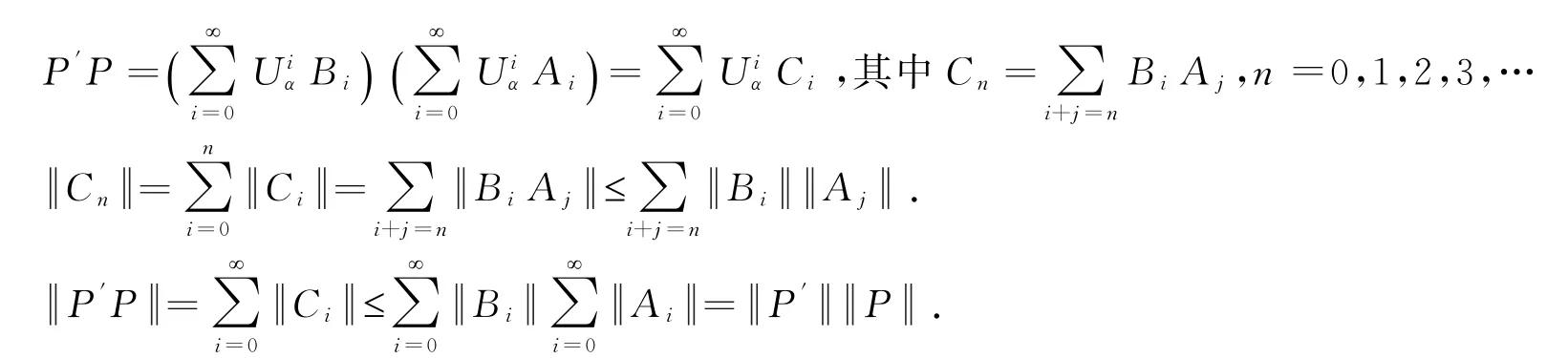
l1(,α)是巴拿赫空间,所以l1(,α)是巴拿赫代数.

定理7 l1(,α)是C*代数.

证设定义了P的对合.因为为C*代数,所以对∀A∈有

所以l1(,α)是C*代数.

推论1 l1(,α)的二次对偶l1(,α)**以一种自然的方式可以看作一个冯·诺依曼代数.

[1]许全华,吐儿德别克,陈泽乾.算子代数与非交换Lp空间引论[M].北京:科学出版社,2010:1-35.

[2]Davidson KR,Katsoulis EG.Semicrossed products of simple C*algebras[J].Math.Ann.,2008(342):515-525.

[3]Turumaru T.Crossed products of operator algebras[J].Tohoku math.,1958(10):355-365.

[4]Peters J.Semicrossed products of C*_algebras[J].Funct.Anual.,1984(59):498-534.

[5]夏道行,吴卓人,严绍宗,等.实变函数论与泛函分析[M].2版.北京:高等教育出版社,2010:52-67.

[6]胡适耕.泛函分析[M].北京:高等教育出版社,2009:3-14.

The completion space of polynomialconstituted by C*-algebra

CHEN Benju
(College of Mathematics Sciences,Chongqing Normal University,Chongqing 401331,China)

In this paper,we add the limit points into skew polynomial algebra,then it become a Banach Space,we show that this Banach Space is a C*algebra.

C*algebra;polynomial algebra;completion;isometrically isomorphic

O177.5

:A

:1671-9476(2015)05-0042-04

10.13450/j.cnkij.zknu.2015.05.011

2015-03-20;

:2015-05-12

陈本菊(1987-),女,重庆合川人,硕士研究生,研究方向:算子代数.