压缩机转子系统的振动可靠性灵敏度设计*

朱丽莎， 张义民， 杜尊令

(1.东北大学机械工程与自动化学院 沈阳，110819) (2.沈阳机床股份有限公司中捷立式加工中心 沈阳，110141)



压缩机转子系统的振动可靠性灵敏度设计*

朱丽莎1， 张义民1， 杜尊令2

(1.东北大学机械工程与自动化学院 沈阳，110819) (2.沈阳机床股份有限公司中捷立式加工中心 沈阳，110141)

为了对压缩机类复杂的转子系统进行可靠性灵敏度设计，探讨可靠度与基本随机变量之间的关系，得到不同随机变量对可靠性的影响程度。通过引入隔离裕度和放大因子的概念，在转子系统动力响应的基础上，预测系统实际隔离裕度与许用隔离裕度。首先，根据许用隔离裕度不超过实际的隔离裕度的关系准则，针对压缩机类转子系统提出了一种基于共振失效的振动可靠性模型；然后，利用神经网络模型代替了有限元模型建立了复杂结构的可靠度与基本随机变量的强非线性关系；最后，以某齿轮转子系统为例，应用可靠性设计理论求解某转子系统危险位置的可靠度，应用可靠性灵敏度理论得到了系统均值灵敏度和方差灵敏度。

可靠性； 隔离裕度； 灵敏度； 振动； 转子系统

引 言

转子系统的可靠性研究是近代机械领域研究的热门课题。目前，对转子系统的可靠性建模，主要分为如下几类：a.基于碰摩失效的可靠性模型,转子的特殊位置在工作状态下由于振动超限造成与定子之间的碰撞摩擦，如转子系统的质量慢变[1]、不对中[2-3]和油膜振荡失稳[4-5]都会造成系统失效；b.基于疲劳失效的可靠性模型,转子由于受到复合应力的作用产生疲劳破坏，在大量疲劳强度分布试验的基础上，采用应力-强度可靠性分析方法，对疲劳寿命进行估算[6]；c.基于频率干涉的可靠性模型[7],根据转子系统的固有频率与激振频率差的绝对值不超过规定值的关系准则，定义了转子系统共振问题的可靠性模式和系统的可靠度；d.基于裂纹失效的转子可靠性模型。胥建群等[8]基于断裂力学的理论对汽轮机转子系统进行了概率分析，将裂纹扩展速率、初始裂纹尺寸和应力变化幅值考虑成独立随机变量，对含有初始缺陷的汽轮机转子进行了寿命预测。

参照美国石油协会标准，笔者提出了一种基于共振失效的振动可靠性模型。此模型引入了隔离裕度和放大因子(amplification factor,简称AF)的概念，通过转子系统的动力响应曲线计算出实际的隔离裕度和许用的隔离裕度。根据转子系统的许用隔离裕度不超过实际的隔离裕度的关系准则，建立了系统的可靠性模型，并基于Edgeworth级数和四阶矩方法，选取某转子系统的危险位置进行了可靠性求解与可靠性灵敏度设计。

1 共振失效机理

API617是美国石油学会针对石油、化学和气体工业用的轴流类、离心类压缩机以及膨胀机-压缩机的整体设计、试验、安装和维护等制定的标准。根据API617中动力学设计的要求，转子系统在横向振动分析过程中，有两种情况会发生共振：a.放大因子大于等于2.5；b.转子系统的实际隔离裕度小于许用的隔离裕度。两种情况同时发生则认为转子系统发生了共振失效。

1.1 放大因子AF的计算方法

转子第1阶临界转速处，放大因子AF定义为

(1)

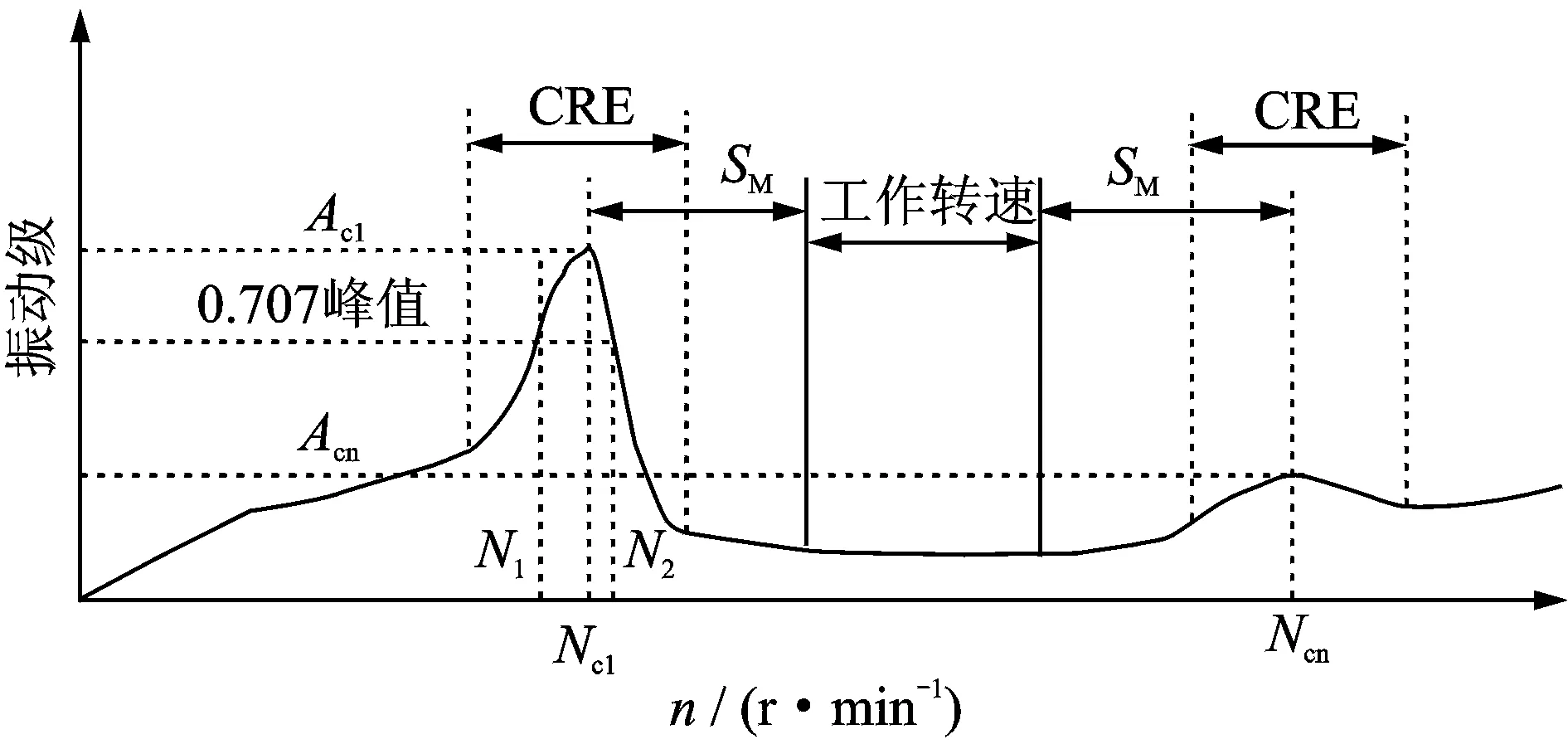
图1 放大因子计算示意图Fig.1 The calculation diagram of amplification factor

放大因子AF的计算示意图如图1所示，并不代表任何实际的转子系统的响应曲线。图中：Nc1为转子第1阶临界转速，中心频率，单位r/min；Ac1为在Nc1处的振幅；Ncn为转子第n阶临界转速；Acn为在Ncn处的振幅；N1为0.707倍振幅峰值时对应的初始转速；N2为0.707倍振幅峰值时对应的终止转速；N2-N1为在“半功率”点峰值宽度；SM为隔离裕度；CRE为临界响应区。

1.2 许用隔离裕度SM′的计算方法

1) 如果在某一临界转速处的AF<2.5，说明该响应在此临界转速下不会发生振动，因此不需要计算隔离裕度。

2) 如果在某一临界转速处的AF≥2.5，并且此临界转速低于工作时的最小转速，该SM′(作为最小转速的百分数)用式(1)计算，得到的值与16相比，取较小者。最小转速为工作转速的85%。

(2)

3) 如果在某一临界转速处的AF≥2.5，并且此临界转速高于工作时的最大连续转速，该SM′(作为最大连续转速的百分数)用式(2)计算，得到的值与26相比，取较小者。最大连续转速取工作转速的115%。

(3)

1.3 实际隔离裕度SM的计算方法

实际隔离裕度与工作转速和临界转速有关，分为两种情况。

1) 当工作转速Nw小于某一临界转速Ncn，则实际隔离裕度为

(4)

其中:Nwmax为最大连续工作转速，为工作转速Nw的115%。

2) 当工作转速Nw大于某一临界转速Ncn，则实际隔离裕度为

(5)

其中：Nwmin为最小连续工作转速，为工作转速Nw的85%。

在确定了转子的临界转速以及振动响应曲线后，就可以计算出系统的放大因子(AF)、实际隔离裕度(SM)和许用隔离裕度(SM′)，进一步判断系统是否失效，流程图如图2所示。

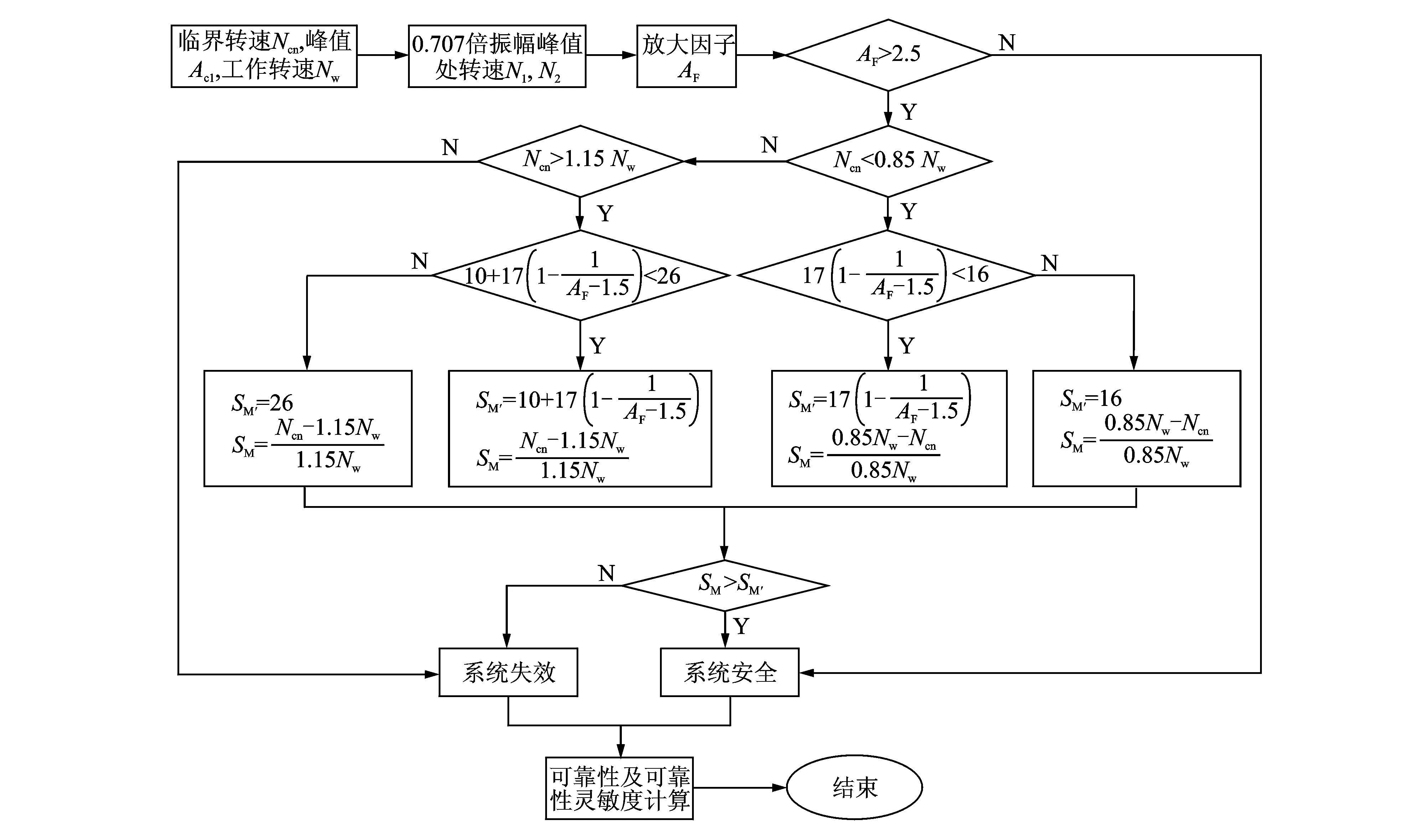
图2 程序流程图Fig.2 Program flow chart

2 可靠性与可靠性灵敏度分析

2.1 极限状态方程

当计算的隔离裕度大于规定的隔离裕度时，系统安全，反之则系统发生共振失效。因此，当工作转速低于临界转速时，极限状态方程的表示为两种形式。

1)SM′<26时

(6a)

2)SM′>26时

(6b)

当工作转速高于临界转速时，极限状态方程的表示为两种形式。

1)SM′<16时

(6c)

2)SM′>16时

(6d)

其中：X为由系统基本参数组成的随机变量向量。

采用人工神经网络技术[9]可以模拟得到函数Ncn(X)，N1(X)，N2(X)与基本随机变量的关系式，进而得到极限状态方程g(X)与基本随机变量之间的非线性显性关系式。

2.2 可靠性设计

根据概率论和随机摄动法的相关知识，状态函数g(·)的前四阶矩[2-4]为

其中：C3和C4分别表示随机向量的三阶中心矩和四阶中心矩;(*)k=(*)⊗(*)⊗…(*)为(*)的kronecker幂。

可靠性指标定义为

(11)

根据Edgeworth级数和四阶矩技术，得到转子系统的可靠度计算公式为

R(β)=P(SM≥SM′)=P(g(X)≥0)=1-F(-β)

(12)

函数F(·)的表达式可以根据Edgeworth级数展开为

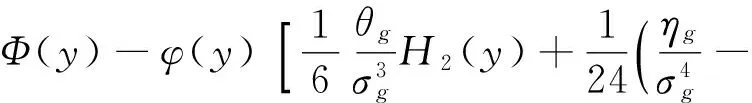
(13)

其中：y=-β；Ф(·)为标准正态分布函数；θg，ηg分别为状态函数的三阶矩和四阶矩；Hi(y)为i阶Hermite多项式，其递推关系为

(14)

2.3 可靠性灵敏度设计

可靠度对基本随机变量均值的灵敏度为

(15)

(16)

其中：In为n×n维单位矩阵;Un×n为置换矩阵;其维数为n2×n2并且每行和每列只有一个元素“1”;“⊗”表示向量矩阵之间的Kronecker乘积。

可靠度对基本随机变量方差的灵敏度为

(17)

在进行结构设计时，设计因素往往很多，而且各因素对结构失效的影响程度又各不相同，影响可靠性的因素之间存在单位不统一的问题，因此需要将可靠性灵敏度进行无量纲化，表示为

(18)

(19)

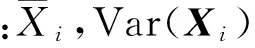
3 算 例

某齿轮转子系统轴承处的不平衡响应曲线如图3所示。

当临界转速低于工作转速时，定义左轴承处共振失效的极限状态方程为

(20)

其中：X为由系统基本参数组成的随机变量向量，X=[β,α,L,k,U]T各个基本随机变量的前四阶矩如表1所示；工作转速Nw假设为基本随机变量，和Nc1(X),N1(X),N2(X)函数均不相关。

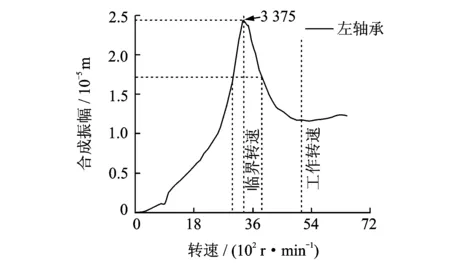
图3 轴承处的不平衡响应曲线Fig.3 Unbalance response curve of bearing

表1 基本随机变量的前四阶矩

将均值代入式(17)可以得到系统的实际隔离裕度与要求的隔离裕度分别为SM=22.201 5；SM′=10.078 1。

因此在随机变量取均值时，系统是安全的。

有限元模型较复杂，用一次确定性的有限元模型进行可靠性设计，假设做106次随机抽样，则需要大约54 Y的时间，这是不符合实际的。因此，笔者在有限样本的基础上，采用神经网络模型代替有限元模型，基于矩方法和Edgeworth级数方法进行可靠性设计。

人工神经网络采用5-8-1的形式，随机抽样共进行100次的拉丁超立方试验，在达到允许误差后，得到的神经网络模型可以代替有限元模型。在基本随机变量均值附近重新设计20组检验样本，将检验样本分别带入有限元模型和神经网络模型，极限状态函数误差如图4所示。

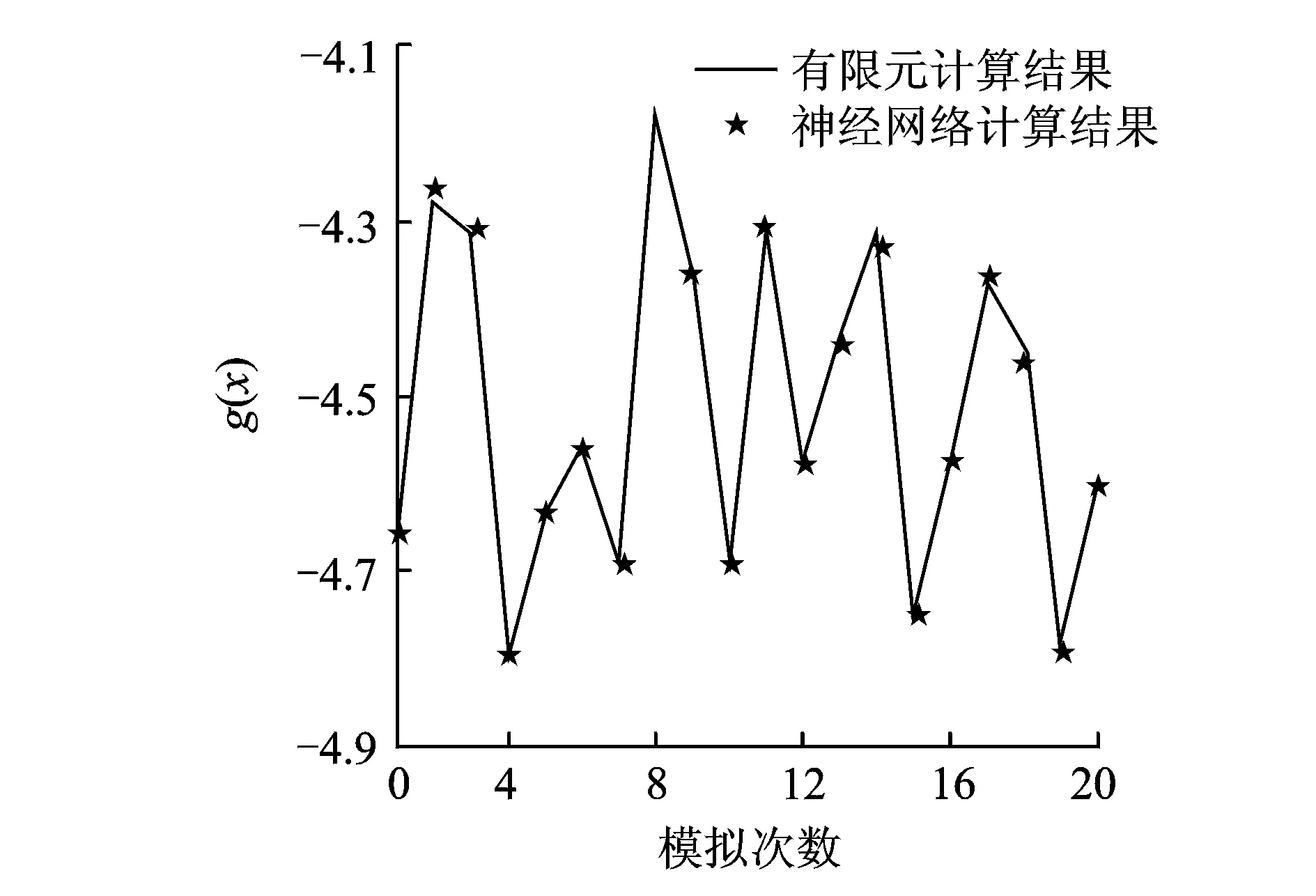
图4 有限元模型与神经网络模型对比结果Fig.4 Comparison of the results between FEM and ANN model

3.1 可靠度计算

基于Edgeworth级数和四阶矩方法对系统进行可靠度求解，得到系统不会发生共振失效的概率。

可靠性指标为β=3.108 2；可靠度为RE=0.999 278。采用蒙特卡洛抽样方法[10]计算，模拟次数为N=100万次，得到的可靠度为RMCS=0.996 367(N=106)。

通过Edgeworth级数方法得到的可靠度RE与采用蒙特卡洛法得到的可靠度RMCS的误差为

通过计算得知，采用Edgeworth级数方法计算可靠度与蒙特卡洛方法的结果误差很小，吻合程度高。但若计算过程全部采用蒙特卡洛方法效率低，采用神经网络与Edgeworth级数结合的方法可以大大提高计算效率[11]。此方法还可以计算系统对基本随机变量的可靠性灵敏度。

3.2 可靠性灵敏度计算

可靠性对基本随机参数向量Xi均值和方差的灵敏度无量纲化后分别表示为

通过计算结果发现，随着均值的增加，系统可靠度增加的基本随机变量为中心距、不平衡量和工作转速。随着均值的增加,系统可靠度降低的基本随机变量为螺旋角、方位角和啮合刚度。

根据各参数无量纲后的均值和方差的计算结果画出灵敏度的直方图如图5，6所示。通过直方图可以形象直观地看到，对系统可靠度影响最大的参数为工作转速，其次为中心距、方位角、不平衡、螺旋角及啮合刚度。

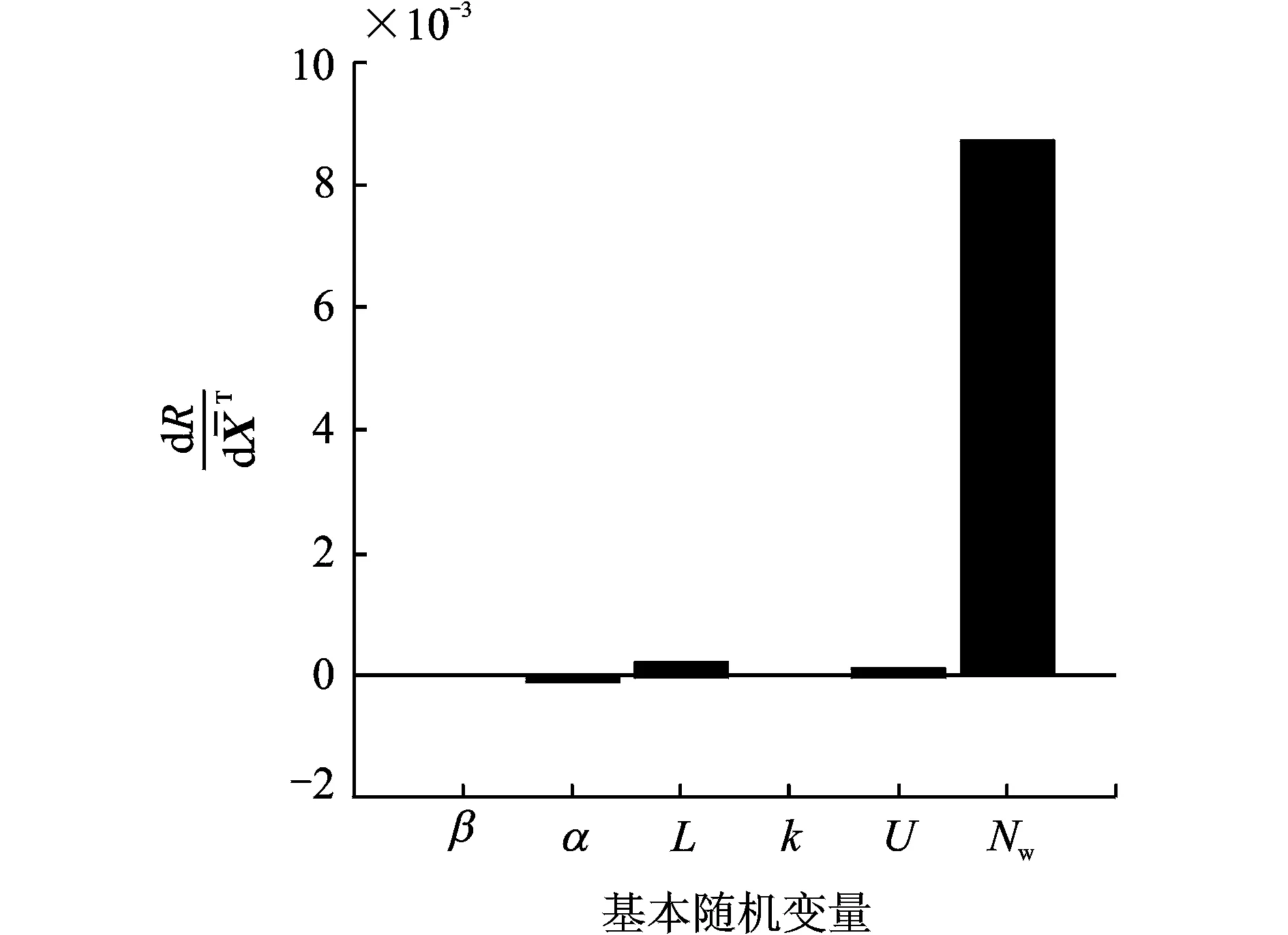
图5 可靠度对基本随机变量均值的灵敏度Fig.5 Reliability sensitivity to the mean value of parameters

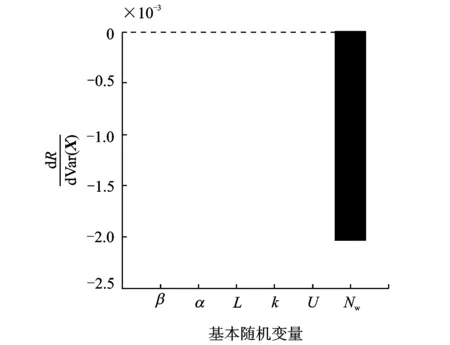
图6 可靠度对基本随机变量方差的灵敏度Fig.6 Reliability sensitivity to the variance of parameters

4 结 论

1) 笔者提出的共振失效依据API标准在工作转速临近临界转速的工况下，根据响应结果曲线进行的二次判定。此方法适用于压缩机和膨胀机类的转子系统建立失效判据。

2) 用神经网络模型代替有限元模型，可以降低求解样本的时间，为大型复杂系统的可靠性求解提供了有效的解决途径。

3) 对实际样本数量不足以统计确定概率分布的情况，基于矩方法和Edgeworth级数的可靠性设计，可以快速准确得到系统可靠度、均值灵敏度和方差灵敏度以及各参数对系统影响排序；针对压缩机类转子系统，在实际工作中最需要注意工作参数、其次是制造和安装参数，最后是啮合参数。

[1] 王宗勇, 吴敬东, 闻邦椿. 质量慢变转子系统的松动与碰摩故障研究[J]. 振动工程学报, 2005, 18(2): 167-171.

Wang Zongyong, Wu Jingdong, Wen Bangchun. Research on pedestal looseness and rub-impact faults of rotor system with slowly varying mass [J]. Journal of Vibration Engineering, 2005, 18(2): 167-171. (in Chinese)

[2] 陈果, 李兴阳. 航空发动机整机振动中的不平衡-不对中-碰摩耦合故障研究[J]. 航空动力学报, 2009, 24(10): 2277-2284.

Chen Guo, Li Xingyang. Study on imbalance-misalignment-rubbing coupling faults in aero-engine vibration [J]. Journal of Aerospace Power, 2009,24(10): 2277-2284. (in Chinese)

[3] 李明. 转角不对中故障的转子系统非线性动力学特征[J]. 振动、测试与诊断, 2011,31(5):552-556.

Li Ming. Nonlinear dynamics characteristics of rotor system with angular misalignment[J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(5): 552-556. (in Chinese)

[4] Wang K S, Chen C S, Huang J J. Dynamic reliability behavior for sliding wear of carburized steel[J]. Reliability Engineering & System Safety, 1997, 58(1): 31-41.

[5] 荆建平, 孟光, 孙毅, 等. 油膜振荡下转子疲劳的损伤力学研究[J]. 机械工程学报, 2004, 40(6): 5-9.

Jing Jianping, Meng Guang, Sun Yi, et al. Study on the fatigue damage of a rotor under oil-whip by continuum damage mechanics[J]. Chinese Journal of Mechanical Engineering, 2004, 40(6): 5-9. (in Chinese)

[6] Sorensen J D, Toft H S. Probabilistic design of wind turbines[J]. Energies, 2010, 3(2): 241-257.

[7] 张义民, 苏长青, 闻邦椿. 转子系统的频率可靠性分析[J]. 振动工程学报, 2009, 22(2): 218-220.

Zhang Yimin, Su Changqing, Wen Bangchun. Natural frequency reliability analysis of rotor system[J]. Journal of Vibration Engineering, 2009, 22(2): 218-220. (in Chinese)

[8] 胥建群, 周克毅, 陈锦涛. 基于概率断裂力学汽轮机转子可靠性研究[J]. 汽轮机技术, 2006, 48(5): 358-360,363.

Xu Jianqun, Zhou Keyi, Chen Jintao. Reliability Study of steam turbine rotor based probability fracture mechanics[J]. Turbine Technology, 2006, 48(5): 358-360,363. (in Chinese)

[9] Cheng Jin, Cai C S, Xiao Rucheng. Application of artificial neural networks to the response prediction of geometrically nonlinear truss structures[J]. Structural Engineering and Mechanics, 2007, 26(3): 251-262.

[10]Fan Haijian, Liang Robert. Reliability-based design of axially loaded drilled shafts using Monte Carlo method[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2013, 37(14): 2223-2238.

[11]朱丽莎, 张义民, 卢昊, 等. 基于神经网络的转子振动可靠性灵敏度分析[J]. 计算机集成制造系统, 2012, 18(1): 149-155.

Zhu Lisha, Zhang Yimin, Lu Hao, et al. Reliability sensitivity analysis of rotor vibration based on neural network[J]. Computer Integrated Manufacturing Systems, 2012, 18(1): 149-155. (in Chinese)

10.16450/j.cnki.issn.1004-6801.2015.05.019

*国家自然科学基金资助项目(U1234208);中央高校基本科研业务费资助项目(N120303002)；辽宁省科技资助项目(20131032)

2013-11-22；

2014-02-27

TB122; TB114.3; TB123

朱丽莎，女，1986年12月生，博士生。主要研究方向为机械可靠性设计。曾发表《直齿轮耦合转子系统的振动可靠性研究》(《振动、测试与诊断》 2013年第33卷第2期)等论文。 E-mail：neulisachu@163.com