基于EEMD排列熵的高速列车转向架故障特征分析*
秦 娜, 蒋 鹏, 孙永奎, 金炜东
(西南交通大学电气工程学院 成都, 610031)
基于EEMD排列熵的高速列车转向架故障特征分析*
秦 娜, 蒋 鹏, 孙永奎, 金炜东
(西南交通大学电气工程学院 成都, 610031)
高速列车转向架关键部件发生机械故障会体现在车体和转向架的振动信号中,为了从监测数据中提取非线性特征参数用于转向架故障状态的反演识别,提出基于聚合经验模态分解排列熵的特征分析方法。首先,对振动信号进行聚合经验模态分解,得到一系列窄带本征模态函数;然后,对原信号和本征模态函数分别计算排列熵值,组成多尺度的复杂性度量特征向量;最后,将高维特征向量输入最小二乘支持向量机分类识别出转向架的工作状态。仿真实验结果表明,该方法在运行速度为200 km/h时,多个通道达到95%以上的识别率,验证了通过聚合经验模态分解排列熵对高速列车转向架机械故障诊断的可行性。
高速列车转向架; 特征提取; 聚合经验模态分解; 排列熵; 最小二乘支持向量机
引 言
转向架是连接车体和轨道的重要机构,其机械性能的恶化轻则导致振动加剧、舒适性降低,重则引起列车运行失稳、脱轨翻车等严重安全事故。目前,国内外对高速列车动车组仍然采用计划定期维修和状态修相结合的检修制度。当设备到达设定运行期限时都会进行常规维修,是一种预防性维修方式[1-2]。随着传感器、通信和信息技术的高速发展,列车转向架故障检测系统获取了海量的运行数据,如何从这些数据中挖掘反映转向架机械故障的本质特征,进而及早发现故障并进行有目的的维修是目前亟待解决的问题。目前,基于数据驱动的高速列车转向架机械故障诊断还处在起步阶段,主要采用简单的振动加速度时域信号峰值、幅值和持续时间作为特征[3]。高速列车属于典型的非线性复杂系统,列车运行产生的振动信号具有明显的非线性非平稳特征[4],采用传统的信号分析方法难以得到满意的效果。因此将智能信息处理方法引入高速列车运行数据的分析和故障诊断是非常有必要的。
经验模态分解(empirical mode decomposition,简称EMD)是近年来提出的一种新的信号分析方法,不依赖于参数的选择,可以通过逐步筛选的方法自适应地将原信号分解为一组本征模态函数(intrinsic mode functions,简称IMFs),IMFs是一组调频或调幅的简单成分信号[5]。当信号具有间歇性或含有冲击成分时,EMD方法体现出致命缺陷——模态混叠问题。聚合经验模态分解(ensemble empirical mode decomposition,简称EEMD)的提出很好地解决了这一问题[6-7]。
排列熵(permutation entropy)是新兴的描述非线性系统复杂度的算法,将不易量化的系统复杂度和紊乱程度用简单的形式定量描述。文献[8]是在原始时域信号的基础上计算排列熵作为反映信号复杂度和随机性的特征参数。文献[9]利用排列熵对信号的变化比较敏感的特性,将其应用在机械振动信号的突变点检测中取得了很好的效果。
笔者的研究对象高速列车转向架机械系统是典型的复杂非线性系统,列车车体和构架上的振动信号受到轨道激扰和转向架上机械部件状态的共同影响,存在复杂的非线性耦合关系。列车振动信号中包含了轨道激励引起的振动,转向架关键部件故障状态引起的振动,车体的固有振动等,仅提取原始混合信号的复杂度不能全面反映信号各模态组份的细节特征。针对高速列车转向架故障振动信号的特点,将聚合经验模态分解和排列熵信息测度相结合用于高速列车转向架故障振动信号的多尺度特征提取。EEMD分解后的IMF是具有特定物理含义的信号,利用相关系数法选取与原信号最相关的模态成分来提取排列熵,可以更好地反映信号在不同尺度和物理意义上的细节复杂度特征。采用最小二乘支持向量机(least squares support vector machine, 简称 LSSVM)进行故障状态识别,实验分析证明了该方法的有效性。
1 聚合经验模态分解
当高速列车发生故障时,振动信号中往往会包含比较多的冲击成分,为了有效地抑制EMD分解过程中的模态混叠现象,采用Wu等[10]提出的聚合经验模态分解。EEMD就是将每个原始信号中加入有限幅值的高斯白噪声,是基于白噪声的统计特性在分解中呈现为自适应二进滤波器。算法的基本原理是:白噪声被添加在时频空间的各个不同尺度的组成成分中,不同尺度的信号就会自动投影到一个由白噪声建立的合适的尺度空间中。利用白噪声多次试验相抵消的统计特性,可采取求平均值的方法来抑制分解结果中噪声的影响[11]。
EEMD算法的步骤为:
1) 初始化聚合次数N,高斯白噪声的幅值系数k,并且使m=1。
2) 计算第m次在信号中加入高斯白噪声后的实验信号
xm(t)=x(t)+k·nm(t)
(1)
3) 利用经验模态分解将加入白噪声后的信号分解为一组本征模态函数(intrinsicmodefunctions,简称IMFs)。
4) 当m 5) 计算N次分解出的各个IMFs均值 (2) 其中:N为经验模态分解的聚合次数;ci,m为由第m次分解得到的第i个IMF。 6) 取每个IMF的N次分解的均值作为最终的本征模态函数。 通过以上步骤,EEMD方法有效克服了模式混叠问题,对传统的经验模态分解进行了重要改进。 衡量系统复杂度的算法有很多,如李雅普诺夫指数,Kaplan-Yorke维数,关联维数和熵等。熵是源于物理学的概念,是对系统内部紊乱程度和产生新模式的可能性的度量。熵值越大,表明系统越复杂。排列熵是近年来提出的一种新算法[12],广泛适用于各种时间序列,并且具有算法简单,运算速度快,对噪声不敏感,计算值稳定等优点[13-14]。 排列熵的计算步骤如下: (3) 其中:j=1,2,…,K;d为嵌入维数;τ为延迟时间;K为重构相空间中重构向量的个数,K=N-(d-1)τ。 对其中第j个重构向量中的数据按从小到大进行排序,得到向量中各元素位置的索引j1,j2,…,jd,即 x(i+(j1-1)τ)≤x(i+(j2-1)τ)≤… ≤x(i+(jd-1)τ) (4) 如果重构向量中存在相等的两个元素,如x(i+(jp-1)τ)=x(i+(jq-1)τ)。 则按照jp和jq原有的顺序,即jp (5) 和其他形式熵的物理意义相似,排列熵也是系统复杂性的度量,熵值越大,系统成分越复杂,越接近随机信号,反之,熵值越小,系统成分越简单规则。熵值的变化可以反映并放大系统动力学性能的变化。 3.1 数据来源及实验方案 实验数据来自西南交通大学牵引动力国家重点实验室,基于多体动力学分析软件Simpack建立某动车组车辆系统非线性动力学模型,车轮踏面外形采用LMA踏面,钢轨采用CN60钢轨,轮对内侧局沿用中国标准1 353mm,充分考虑轮轨接触几何非线性、轮轨蠕滑非线性和非线性悬挂,该车轮由1个车体、2个构架、4个轮对、8个转臂和2个牵引拉杆,全车共62个自由度,仿真采用武汉-广州客运专线实测轨道激扰谱进行分析。转向架故障工况主要涉及横向减振器故障、抗蛇行减振器故障、空气弹簧失气和原车方案(无故障状态)。每种工况下运行速度按照40,80,120,140,160,200km/h,…,递增,直至失稳。每种速度下运行约3.6min,采样频率为243Hz。 仿真实验记录了列车及转向架上各相关部位的振动信号,主要包括车体、构架、轴箱上各个部位横向、纵向和垂向振动加速度和车体、构架、轮对、一系、二系各部位三个方向的振动位移,共得到58个通道数据,每个通道代表列车和转向架上不同的采样位置。图1为采自高速列车转向架端部横向振动加速度信号的4种典型工况振动信号时域和幅值谱图。 图1 4种工况的时域信号和幅值谱Fig.1 Time-domain signal and amplitude spectrum of four working conditions 由图1可以看出,抗蛇行减振器故障和横向减振器故障的时域信号和频域信号相比原车和均具有更强的规律性,主要原因是列车无故障时振动信号主要包含车体固有机械振动和轨道激励等随机因素引起的振动,当故障发生时,减振器的失效使列车在特定的方向和频率上振动加剧而产生横向蛇行、点头、侧滚等周期性较强的非正常运动。 3.2 信号处理流程 由机车车辆动力学原理可知,列车转向架故障振动信号是典型的非线性非平稳信号,故障特征主要体现在低频部分。首先,将原始振动信号进行简单的小波包消噪处理;然后,对消噪后的信号进行聚合经验模态分解,根据信号自身的特点自适应地分解为一系列成分相对简单的本征模态函数,这些IMFs按照频段从高到低的顺序排列。对原始信号和EEMD分解得到的IMFs选取合适的嵌入维数和延迟时间进行相空间重构,计算反映各尺度信号复杂度特征的排列熵测度值,组成高维特征向量。将这个高维特征向量输入到最小二乘支持向量机中进行分类识别,得到高速列车转向架的故障状态识别结果。图2为信号处理流程图。 图2 信号处理流程图 3.3 信号的聚合经验模态分解 消噪后的振动信号采用EEMD进行分解,图3为横向减振器故障状态下构架上1架1位横向振动加速度信号的EEMD分解结果的前8个IMFs分量。理想情况下,每个IMF分量都是一个简单的平稳信号,代表了原信号中的特征成分之一。由于受到包络估计函数,白噪声幅值系数和聚合迭代次数等参数选择的影响,分解结果中不可避免地存在虚假成分。为了从IMFs中选取出最能反映原信号特征的分量,采用相关系数法求出各IMFs与原信号的相关系数。实验结果表明,前6个IMFs与原信号的相关系数均大于0.1,后面的IMFs相关系数都小于0.1且呈现逐层降低趋势。因此,选取原信号和前6个IMFs作为进一步特征提取的对象。 图3 信号EEMD分解结果Fig.3 Decomposition result by EEMD 3.4 排列熵特征提取 在排列熵的计算中,参数的选择对熵值的计算结果会产生影响。重构相空间维数m的值越大越能体现信号动态演化的过程。按照经验[15],选取d=5,τ=4计算原始信号和EEMD分解后的前6个IMFs的排列熵值。4种工况的各尺度排列熵计算结果如表1所示。 表1 4种工况的各尺度排列熵特征值 Tab.1 Multiscale permutation entropy of four working conditions 工况原信号IMF1IMF2IMF3IMF4IMF5IMF6原车3.7304.5714.3303.8193.0132.2121.589空气弹簧失气4.5174.3084.0224.4753.0372.3241.649抗蛇行减振器故障3.6104.6784.4354.1663.0901.9351.502横向减振器故障4.5974.6184.2054.4933.1602.3541.460 对4种工况的仿真数据各截取70个样本信号,每个样本729个采样点,运行速度为200 km/h。对所有的样本计算EEMD分解后的各尺度排列熵特征,构成280×7的特征矩阵。为了更好地展现样本在高维特征空间中的类内聚集性和类间分离性,图4给出了构架上1架1位横向加速度信号的排列熵特征在三维特征空间中的分布情况(200 km通道7)。可以看出,EEMD排列熵特征在高维特征空间上拥有良好的类内聚集性,这是分类识别的基础。 图4 排列熵特征的3维空间散点图Fig.4 Scatter diagram of permutation entropy in 3-D feature space 3.5 最小二乘支持向量机故障状态识别 由于计算量巨大,仿真实验得到的样本数比较有限,为了实现高速列车转向架故障状态自动分类识别,采用最小二乘支持向量机作为分类器。最小二乘支持向量机比传统支持向量机在不降低识别精度的前提下具有更快的收敛速度[16]。将7维EEMD排列熵特征向量作为最小二乘支持向量机的输入,得到运行速度为200 km/h下识别率如表2所示。不同通道的正确识别率差距较大,说明车体构架上不同位置对转向架故障的敏感程度不同,这是由振动的传导路径和机车及转向架的机械结构决定的。从表2可以看出,识别率较高位置集中体现在构架上横向加速度、轴箱上加速度和车体位移信号,与车辆动力学结论相一致。 表2 不同位置的故障识别率 Tab.2 Fault recognition rate of different position % 通道数识别率1~1083.082.183.040.267.969.699.153.697.374.111~2098.292.910067.093.878.678.667.968.898.221~3052.710079.550.010099.146.410072.330.431~4098.277.798.286.697.587.571.458.979.560.741~5080.458.071.450.967.943.875.049.165.269.651~5873.274.186.672.383.982.181.384.8 从图1可以看出,4种典型工况下振动信号在时域和频域上体现出不同程度的差异,但是直观上并不能很好地区分抗蛇行减振器故障和横向减振器故障以及原车与空气弹簧失气。笔者采用EEMD和排列熵相结合的方法,对振动信号进行处理后可以得到量化的故障特征参数,通过LSSVM实现故障自动识别,在多个传感器通道均得到了满意的识别率。为了验证EEMD排列熵特征提取方法的可行性,表3给出了转向架不同位置两种特征提取方法得到的识别结果。可以看出,EEMD排列熵特征在转向架多数位置上得到了更高的识别率。 3.6 参数渐变故障的EEMD排列熵特征 由于在实际的机械系统中,阻尼部件的性能退化往往是一个渐变的过程,因此探讨机械部件的参数退化与信号特征变化之间的关系是很有必要的。 表3 不同特征不同位置的识别率比较 实验选取抗蛇行减振器和横向减振器故障作为例子进行了仿真计算,在其他条件相同的情况下,依次改变减振器的阻尼参数90%,80%,…,10%,其中参数10%接近全故障。每种参数下选取30个样本,每个样本包含729个采样点。将每个样本进行预处理和特征提取。图5为故障参数变化时EEMD排列熵特征的三维空间散点图。 图5 故障参数变化时特征在3维空间上的散点图Fig.5 Scatter diagram of permutation entropy with change fault parameter 从图5可以明显地看出特征跟随故障参数退化而渐变的过程,故障参数退化的初期(约90%)、中期(约50%)和后期(约10%)分别表现出不同的EEMD排列熵特征值。因此,EEMD排列熵可以很好地反映高速列车转向架阻尼部件参数退化过程。 3.7 速度变化时的EEMD排列熵特征 为了研究EEMD排列熵特征受列车运行速度变化影响的情况,实验选取横向减振器全故障工况进行仿真计算,依次改变高速列车的运行速度40,80,120,160,200 km/h。图6为速度变化时构架1架中部横向加速度信号的EEMD排列熵特征在3维空间上的散点图。可以看出,列车运行在低速、中速、高速时,运行速度的变化会引起转向架和车体上振动信号的变化,排列熵很好地反应了这种变化。 图6 速度变化时特征在3维空间上的散点图Fig.6 Scatter diagram of permutation entropy with change speed 笔者提出了一种基于EEMD和排列熵的高速列车转向架机械故障特征提取方法,选用适合于小样本分类、训练速度更快的最小二乘支持向量机进行故障状态的分类识别,取得了满意的识别效果。传统EMD分解方法会产生端点效应、模式混叠问题,选用改进算法EEMD对故障振动信号进行时频分解,采用相关分析法选取和原始信号最接近的6个IMFs。用排列熵对原始信号和选出的IMFs分别进行复杂度分析,以各个尺度上的排列熵值构成反映原信号复杂度的高维特征向量,并输入到LSSVM进行故障状态识别,和传统的近似熵方法相比得到了更高的识别率。同时,EEMD排列熵特征可以很好地反映故障参数渐变和速度变化对振动信号的影响情况。仿真实验证明,该方法可以作为高速列车转向架机械故障分析的一种有效途径。 [1] 蒋贵山. 提高动车组运行安全性的转向架关键检修技术探讨[J]. 铁道车辆, 2013,51(5): 21-24. Jiang Guishan. Discussion of the key Technologies in inspection and repair of bogies to improve the operation safety of multiple units [J]. Rolling Stock, 2013,51(5): 21-24.(in Chinese) [2] Hayashi Y, Tsunashima H, Marumo Y. Fault detection on railway vehicle suspension systems using multiple-model approach[J]. Journal of Mechanical Systems for Transportaion and Logistics,2008,4(1):88-99. [3] 大庭拓也,蔡千华. 基于振动分析的新干线转向架的状态监视[J]. 国外铁道车辆, 2013,50(3):32-40. Dating Tuoye, Cai Qianhua. The condition monitoring for shinkansen bogies based on vibration analysis[J]. Foreign Rolling Stock, 2013,50(3):32-40. (in Chinese) [4] 王小亮,李立,张卫华. 高速列车垂向振动的模拟器再现方法研究[J]. 振动、测试与诊断, 2009,29(1):101-104. Wang Xiaoliang, Li Li, Zhang Weihua. Fuzzy self-tuning based washout algorithm for simulator of high speed locomotive vertical vibration[J]. Journal of Vibration, Measurement & Diagnosis, 2009,29(1):101-104. (in Chinese) [5] Bin G F, Gao J J, Li X J, et al. Early fault diagnosis of rotating machinery based on wavelet packets-Empirical mode decomposition feature extraction and neural network[J]. Mechanical Systems and Signal Processing, 2012, 27(2):696-711. [6] Lei Yaguo, He Zhengjia, Zi Yanyang. EEMD method and WNN for fault diagnosis of locomotive roller bearings[J]. Expert Systems with Applications,2011, 38(6):7334-7341. [7] An Xueli, Jiang Dongxiang,Li Shaohua, et al. Application of the ensemble empirical mode decomposition and Hilbert transform to pedestal looseness study of direct-drive wind turbine[J]. Energy,2011, 36(9):5508-5520. [8] Xiang Shuiying, Wei Pan, Yan Lianshan, et al. Quantifying chaotic unpredictability of vertical-cavity surface-emitting lasers with polarized optical feedback via permutation entropy[J]. IEEE Journal of Selected Topics in Quantum Electronics, 2011, 17(5):1212-1219. [9] 冯辅周,饶国强,司爱威,等. 排列熵算法研究及其在振动信号突变检测中的应用[J]. 振动工程学报, 2012,25(2):221-224. Feng Fuzhou, Rao Guoqiang,Si Aiwei,et al. Research and appl ication of the arithmetic of PE in testing the sudden change of vibration signal[J]. Journal of Vibration Engineering, 2012,25(2):221-224. (in Chinese) [10]Wu Zhaohua, Huang N E. Ensemble empirical mode decomposition:a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis,2009, 1(1):1-41. [11]Matj Z, Samo Z, Ivan P. Non-linear multivariate and multiscale monitoring and signal denoising strategy using kernel principal component analysis combined with ensemble empirical mode decomposition method[J]. Mechanical Systems and Signal Processing, 2011, 25(7):2631-2653. [12]Bandt C, Pompe B. Permutation entropy:a natural complexity measure for time series[J]. Physical Review Letters,2002, 88(17):174102. [13]冯辅周,司爱威,饶国强,等. 基于小波相关排列熵的轴承早期故障诊断技术[J]. 机械工程学报, 2012,48(13):73-79. Feng Fuzhou, Si Aaiwei, Rao Guoqiang, et al. Early fault diagnosis technology for bearing based on wavelet correlation permutation entropy[J]. Journal of Mechanical Engineering, 2012,48(13):73-79. (in Chinese) [14]Zunino L, Rosso O A, Soriano M C. Characterizing the hyperchaotic dynamics of a semiconductor laser subject to optical feedback via permutation entropy[J]. IEEE Journal of Selected Topics in Quantum Electronics,2011, 17(5):1250-1257. [15]刘永斌,龙潜,冯志华,等. 一种非平稳-非线性振动信号检测方法的研究[J]. 振动与冲击,2007,26(12):131-134. Liu Yongbin, Long Qian, Feng Zhihua,et al. Detection method for nonlinear and non-stationary signals[J]. Journal of Vibration and Shock, 2007,26(12):131-134.(in Chinese) [16]李兵,张培林,任国全,等. 运用EMD和GA-SVM的齿轮故障特征提取与选择[J]. 振动、测试与诊断,2009,29(4):445-448. Li Bing, Zhang Peilin, Ren Guoquan, et al. Gear fault diagnosis using empirical mode decomposition, genetic algorithm and support vector machine[J]. Journal of Vibration, Measurement & Diagnosis,2009,29(4):445-448. (in Chinese) 10.16450/j.cnki.issn.1004-6801.2015.05.013 *国家自然科学基金重点资助项目(61134002);中央高校基本科研业务费专项资金资助项目(2682015CX025) 2013-10-15; 2013-12-13 TP206+.3 秦娜,女,1978年9月生,博士、讲师。主要研究方向为智能信号处理与模式识别。曾发表《高速列车转向架故障信号的聚合经验模态分解和模糊熵特征分析》(《控制理论与应用》2014年第31卷第9期)等论文。 E-mail:qinna@swjtu.cn2 排列熵特征提取

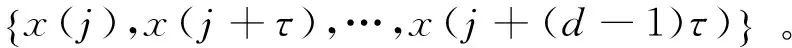



3 高速列车转向架故障信号分析

Fig.2 Signal processing flow chart




4 结束语


