基于神经网络的有限转角力矩电动机滑模控制

许 辉，王自强

(北京航空航天大学，北京100191)

0 引 言

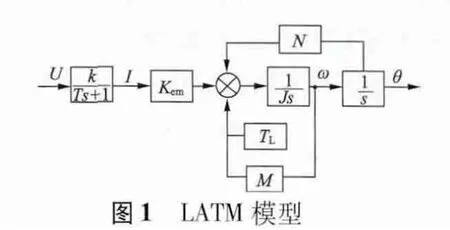
随着电机设计技术的发展，需要具有各种不同工作形式的电机以满足自动控制系统的要求，20 世纪70 年代起发展起来了一种新型电机——有限转角力矩电动机(以下简称LATM)［1］，它与传统电机的运动方式有所不同，能在有限转角范围内围绕某一特定中心位置做周期性往复运动，从而提供了一种特殊的工作方式。有限转角力矩电动机相比传统的力矩电动机，具有结构简单、输出力矩大、可靠性高、波动小且易于控制等突出的优点。由这类电机构成的位置伺服系统频带宽、体积小、动态响应快，适用于扫描型红外成像系统等高精度、高性能要求的控制系统。但由于有限转角力矩电动机是多变量、非线性的复杂对象，而传统的的PI 控制不能很好地控制它［2］，因而在此选择滑模控制［13］来满足其控制性能。滑模变结构控制广泛应用于电机控制领域，可以应用在同步电机、异步电机以及直流电机中［3］。

滑模控制(以下简称SMC)对系统的精度要求不高，对外部扰动、内部参数摄动具有强鲁棒性［4］，因而近年来成为许多学者青睐的控制方法，已经比较普遍用于永磁同步电动机［5］、直流电动机等系统中。国外对滑模变结构控制的研究时间比较早，研究的范围也很广，比如，既有对一般非线性系统的滑模控制［6］，也有针对的新型积分滑模控制同步电机的新型积分滑模控制［7］;为了能够消除谐振、减少误差，使RBF 神经网络控制与滑模控制相结合，设计了基于RBF 网络的滑模控制器［8-9］，很好地解决的存在的问题。近年来，国内也有很多用滑模控制来控制系统的论文，文献［12］针对风电机组输出功率的不稳定，对桨距角进行了RBF 神经网络滑模控制，结果表明，该控制很好地提高了系统的鲁棒性，也有效地减少了抖振现象。文献［14］中，为了减少负载扰动对永磁同步电动机的影响，作者设计了负载转矩滑模控制器，并用实验方法验证了系统的抗干扰能力。

本文结合滑模变结构控制和RBF 神经网络控制来控制此系统，得到系统控制率，并用Lyapunov方法证明控制率的稳定性。最后进行了实验研究和仿真分析［11］，结构表明控制方法能很好地提高系统的鲁棒性，改善了系统的动态性能。

1 LATM 的数学模型

LATM 是近几十年迅速发展起来的一种特种电动机，在跟踪、红外及激光成像等系统中获得了广泛的应用。LATM 在结构和运动形式上有别于一般的旋转电机，它是在一定转角范围内作往复运动。这种电机具有良好的调节特性和机械特性，能直接驱动负载实现快速往复运动。

LATM 的磁场由永磁体建立，电机各个磁路的磁阻随着转子位置的改变而改变，其遵循“磁阻最小原理”，即磁通总是沿着磁阻最小的路径闭合。LATM 采用直流电压控制，电压方程如下:

LATM 的转矩方程:

LATM 的运动方程:

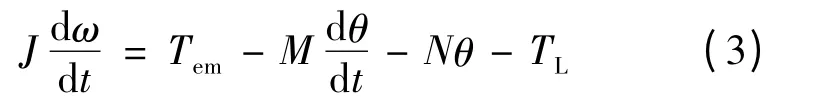
且:

式中:J 为转动惯量;Tem为电磁转矩;TL为负载转矩;ω 为角速度;I 为电枢电流;M 为速度阻尼系数;N 为挠性枢轴扭转刚度;k 为电路放大倍数;T 为电路延时时间常数;Kem为电磁转矩系数。

对式(1)～式(4)做Laplace 变换，可得到电机模型:

由式(1)～式(4)可得电机状态矩阵:

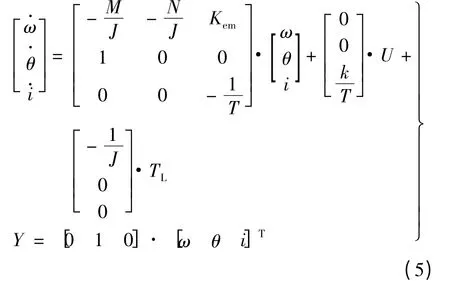
状态方程也可写:

式中:D(T)为外界干扰，且满足|D(T)|≤D。

2 控制策略

神经网络是一种具有高度非线性的连续时间系统，它对非线性系统有很好的映射能力，并且有着强大的学习功能。在滑模变结构控制中添加神经网络控制，可以实现自适应滑模控制。

2.1 RBF 神经网络

Darken C 和Moody J 在20 世纪80 年代提出了RBF 神经网络模型，它是具有单隐层的三层前馈网络，图2 为其结构图。已经证明，RBF 网络具有万能逼近的性能［11］，因而可以很好地应用在非线性度高的电机上，比如本文中的有限转角力矩电动机。

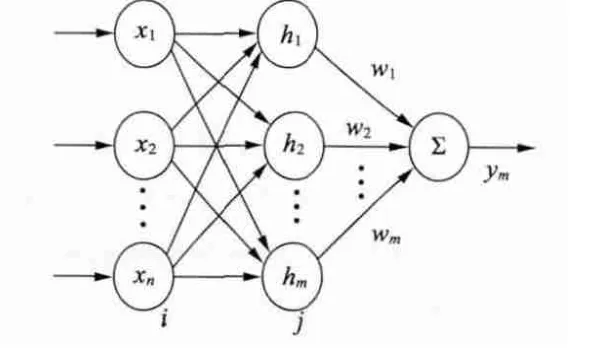
图2 径向基神经网络结构图

用RBF 神经网络逼近函数f，则逼近算法:

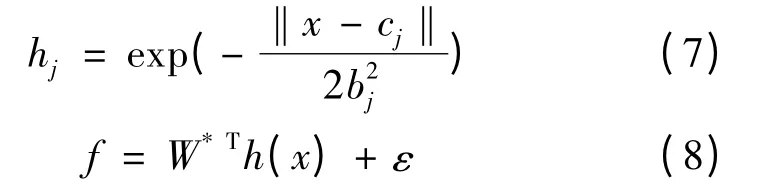
式中:x 为网络输入;j 为网络隐含层第j 个节点;h =［hj］T为高斯函数;W*为网络理想权值;ε 为网络逼近误差，且ε≤εN。

2.2 控制器设计

本节进行控制器的设计，定义角速度跟踪误差:

式中:X1d为理想跟踪指令。

式(7)的微分:

设计滑模面:

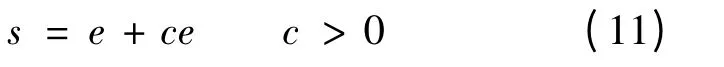
由以上各式可得:

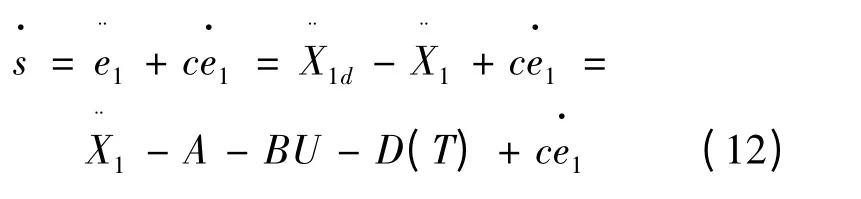
则可设计控制律率:

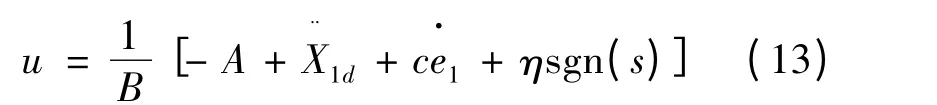
式中:sgn(s)为符号函数;η 为学习效率，η ＞0。

由于参数J 是未知参数，所以我们采用RBF 神经网络来逼近A(J)，以实现稳定控制。

RBF 神经网络输入取x=［e1e·1］T，则RBF 网络输出:

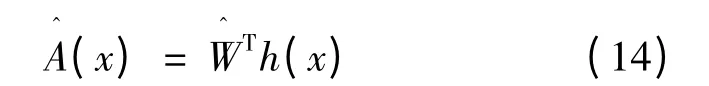
式中:h(x)为RBF 神经网络的高斯函数。

将式(14)代入式(13)中，则控制率:

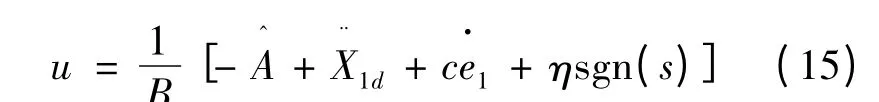
将式(15)代入式(12)中，得到:

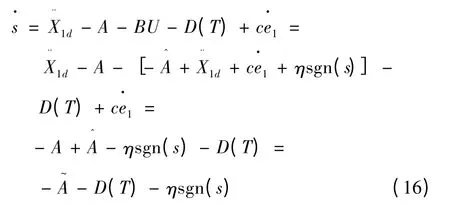
其中:

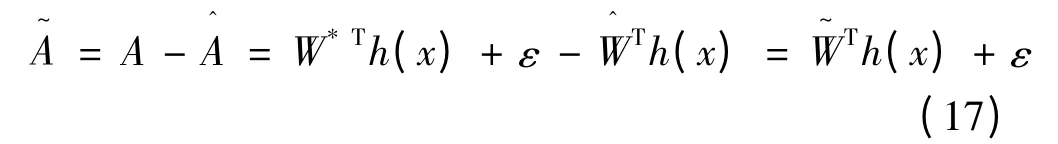
为了实现有限转角力矩电动机的动力学系统的稳定控制，选取Lyapunov 函数:

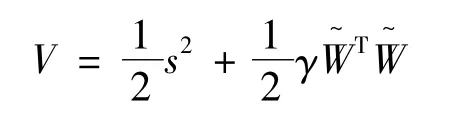
式中:γ ＞0。

对Lyapunov 函数求导，结合式(15)和式(16)，可以得到:

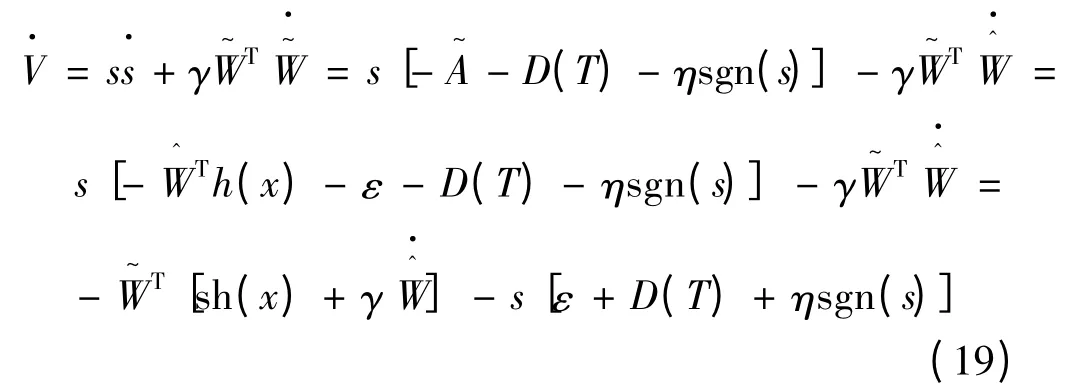
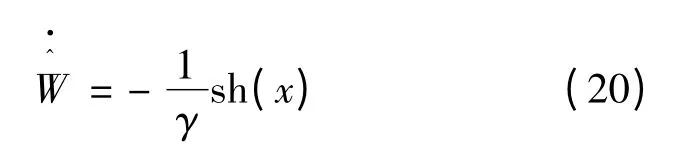
2.3 系统稳定性分析

对控制系统来说，稳定性是十分重要的。对一般系统而言，如果满足滑模的存在及可达条件，则运动进入滑模动态区以后，就开始滑模运动，对通常的反馈系统而言，都希望滑模运动是渐进稳定的，下面就来证明本文中的控制方法是稳定的。

由式(19)与式(20)可知:

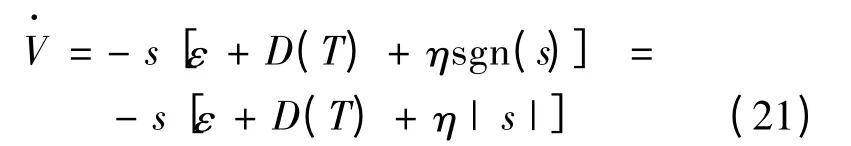
由于逼近误差ε 可以限制得足够小，取η≥εN+D，可得≤0，所以是负定的，此控制方法是稳定的。

3 仿真分析

为了验证以上理论研究的准确性，下面对有限转角力矩电动机控制系统进行了仿真研究。电机参数:速度阻尼系数M =3.88 ×10-5N·m·rad-1·s;挠性枢轴扭转刚度N=0.028 9 N·m/rad;电路延时时间常数T =9.25 ×10-5s;电路放大倍数k =0.474;电磁转矩系数Kem=0.032 N·m/A。

有限转角力矩电动机的滑模控制系统结构图如图3 所示。

首先利用MATLAB/Simulink 建立仿真模型，电机模型由MATLAB/Simulink 中的元件以及电机的数学模型搭建，RBF 网络及滑模控制器用MATLAB语言编程，M 函数实现。

本文采用两种控制方法对比的方法来验证所用算法的有效性。控制方法1 是传统的PID 控制方法，控制方法2 是基于RBF 神经网络的滑模控制方法。两种控制器具有相同的误差反馈增益。

为了着重突出本文中提出的基于RBF 神经网络的滑模控制器的性能优点，分别设计了以下几组仿真进行比较:

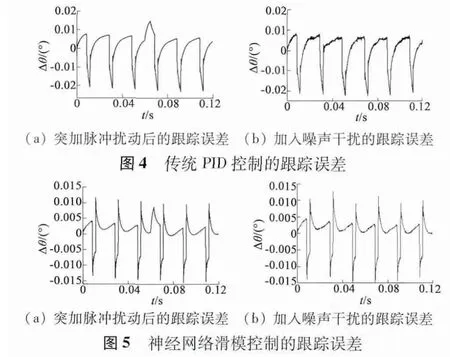
(1)为了比较系统的稳定性和快速性，在控制过程中，相同的时间点突然加入一个脉冲扰动，通过角度跟踪误差，比较传统PID 控制器与神经网络控制器的性能;

(2)为了比较传统PID 控制器与神经网络控制器的抖振性能，在控制仿真的整个过程中，加入相同的噪声干扰，通过角度跟踪误差，来比较两种控制方法的优劣。

由图4(a)与图5(a)可以看出，在0.06 s 时加入一个脉冲干扰，图4(a)中传统PID 控制的系统的跟踪误差有一个明显的增大，差不多经过一个周期才回归正常，并且扰动峰值远超出了正常时误差峰值;而在图5(a)中，由RBF 神经滑模控制的系统的跟踪误差虽有小幅增大，但很快趋于稳定，其扰动峰值也没有超过正常时的误差峰值。说明RBF 神经滑模控制具有更好的系统稳定性和快速性。由图4(b)与图5(b)的仿真图可知，当仿真过程都加上噪声干扰后，传统PID 控制器的跟踪误差有0.023°，而基于RBF 神经网络的滑模控制器的跟踪误差只有0.015°。在相同的工作状态下，相对于传统PID控制器，基于RBF 神经网络的滑模控制器的跟踪性能提升了34.8%。

4 实验验证

为了验证神经网络滑模控制器的优越性以及可行性，通过搭建控制实验平台进行实验研究。有限转角力矩电动机伺服系统主要包括有限转角电机和控制器两部分组成，如图6 所示，控制器部分采用AD公司定点DSP中比较新的16位定点DSP，ADSP -2189。

图6 实验平台

图7 为突加脉冲扰动后的跟踪误差曲线。从图7 中可以看出，用传统PID 控制的跟踪误差曲线沿坐标轴向下方向有很明显的脉动，而神经滑模控制的跟踪误差曲线则比较平缓，没有较大脉动，这个结果与仿真结果基本一致。

图8 为整个实验过程加入噪声干扰后的跟踪误差曲线。从图8 可以看出，神经网络滑模控制所产生的误差远远小于传统PID 控制所产生的误差，误差基本上减少了50%以上，这与前面的仿真结果一致。

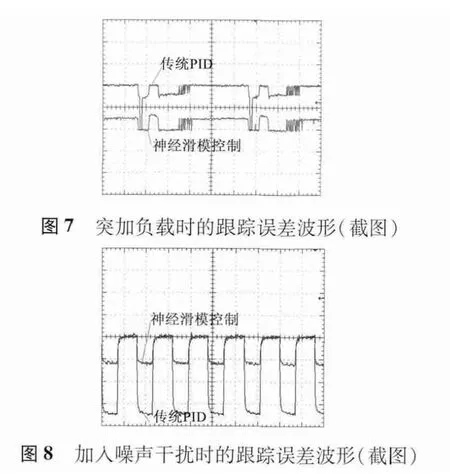
从实验部分可以看出，神经滑模控制器对于长时间工作在干扰环境下的电机，有很好的控制能力，大大增强了系统的鲁棒性。

5 结 语

本文针对有限转角力矩电动机系统存在的参数不确定性和非线性，建立了有限转角力矩电动机的数学模型，提出了一种基于RBF 神经网络的有限转角力矩电动机滑模控制方法，对于控制系统存在的抖振现象，建立了其控制律，并采用李雅普诺夫理论证明了方法的收敛性。该方法克服了系统的非线性和对电机参数的依赖性，对负载扰动和电机参数扰动具有较强的鲁棒性。理论分析和仿真分析均证明所提控制方案的有效性。最后通过实验验证了仿真结果的正确性，以及控制策略的可行性。从文中可以看出，神经滑模控制很适合控制长时间工作在干扰环境中的电机，能很好地提高系统的稳定性。

［1］ ZHANG Y，SMITH I R，KETTLWBOROUGH G.Performance evaluation for a limited-angle torque motor［J］. IEEE/ASME Transactions on Mechatronics，1999，14(3):335 -339.

［2］ DU Chun-yang，LI Tie-cai，CAO Zheng-cai.Accurate tracking control of a limited angel torque motor［J］. Electric machines and Power Systems，1999，27(11):1191 -1199.

［3］ UTKIN A，GULDNER J，SHI J X.Sliding mode control in electromechanical systems［M］.Oxon，UK:Taylor ＆ Francis，1999.

［4］ UTKIN V I. Variable structure systems with sliding modes［J］.IEEE Transactions on Automatic Control，1997，22(2):212-222.

［5］ 朱家厅，王莉娜，薛飞.永磁同步电机的滑模PI 模糊逻辑控制［J］.电气传动，2013，43(7):43 -48.

［6］ BOLIVARD M R，ZINOBER A S I，SIRA-RAMIREZ H.Dynamical adaptive sliding mode output tracking control of a class of nonlinear systems［J］. International Journal of Robust and Nonlinear Control，1997，7(4):387 -405.性积分滑模控制［J］.北京航空航天大学学报，2014，40(3):321 -326.

［7］ LIN F J，CHIU S L，SHYU K K. Novel sliding mode controller for synchronous motor drive［J］. IEEE Transactions on Aerospace and Electronic Systems，1998，34(2):532 -542.

［8］ HUANG S J，HUANG K S，CHIOU K C. Development and application of a novel radial basis function sliding mode controller［J］.Mechatronics，2003，13(4):313 -329.

［9］ LIN S C，CHEN Y Y. RBF network based sliding mode control［C］//IEEE International Conference on Systems，Man，and Cybernetics，1994:1957 -1961.

［10］ 韩松杉，焦宗夏，汪成文，等. 基于神经网络的电液转台非线

［11］ 刘金琨.滑模变结构控制MATLAB 仿真［M］.北京:清华大学出版社，2005:188 -235.

［12］ 秦斌，周浩，杜康，等.基于RBF 网络的风电记住变桨距滑模控制［J］.电工技术学报，2013，28(5):37 -41.

［13］ 付子义，李华群，王振锋.基于神经网络推力观测器的永磁直线电机滑模控制［J］.电气传动，2009，39(11):48 -51.

［14］ 张晓光，孙力，赵克.基于负载转矩滑模观测的永磁同步电机滑模控制［J］.中国电机工程学报，2012，32(3):111 -116.