多跨钢结构人行吊桥桥面板的等效模型研究
胡元伦, 盛宏玉
(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)
夹层板由上下面板和中间的夹芯组成。上下面板几乎提供了夹层板全部的弯曲刚度和平面内的拉伸刚度,肋板则提供了夹层板的横向剪切刚度,同时还起到稳定面板、防止局部屈曲的作用,整体结构类似工字梁的受力原理。夹层板具有优良的比强度和比刚度,良好的抗疲劳、阻尼减振、隔声、吸声、隔热等性能。由于以上优点,夹层板结构在工程中得到了广泛的应用[1-2]。国内外众多学者对夹层板结构进行了一系列研究工作。文献[3]基于低阶剪切理论提出了一种夹层板的等效分析方法;文献[4-5]对夹层结构进行了一系列的实验研究;文献[6]对脱硫塔结构抗震分析的简化模型进行了分析研究;文献[7]运用多种等效理论对夹层板进行了有限元静力分析;文献[8]基于三明治等效理论进行了多夹芯板的动力学分析。在现有的商用有限元分析软件中没有夹芯结构的单元库,而采用实体单元建模难度较大,建模工作量和计算工作量都非常大,因此需要对夹芯结构进行等效处理,建立简单易行而又准确可靠的等效模型,以达到快速计算桥梁特性和提高设计效率的目的。等效模型既要反映结构的主要特征,又不能过于精细和复杂,否则很难在工程实际中加以推广应用。建立等效计算模型关键是寻找一个合理的等效原则,使得等效模型与原模型的动力特性尽可能保持一致。本文以某市博物馆中庭内部多跨折形钢结构人行吊桥为研究对象,从保证等效桥面板与原结构桥面板的抗弯刚度、转动惯量、线密度保持一致的原则出发,对等效模型进行了分析研究,并通过计算说明了等效模型的合理性。
1 工程概况
某市博物馆的主体结构由外围的型钢混凝土框架支撑体系、矩形管桁架屋盖和中庭的多跨折形吊桥组成,其中吊桥的俯视图如图1所示。该吊桥的5段桥面可分为2个部分,第1部分由Ⅰ、Ⅱ2段桥面组成,其中2个固定端通过连接件固结在主体结构的墙体上,2段桥面的1个连接端通过吊杆等支撑构件而自由悬挑;第2部分由Ⅲ、Ⅳ、Ⅴ3段桥面组成,其中有3个固定端通过连接件固结在主体结构的墙体上,3段桥面的2个连接端通过吊杆等支撑构件而自由悬挑。为支撑整个吊桥,桥面上共有竖向吊杆37根(直径60mm)、3个悬臂端共有斜杆19根(直径100mm);竖杆上端用耳板和销与矩形管桁架屋盖连接,竖杆下端用耳板和销与5段桥面板连接。

图1 博物馆吊桥俯视示意图
2 等效模型参数推导
本文采用有限元软件ANSYS建立吊桥的计算模型进行仿真模拟,竖杆和斜杆采用杆单元,箱型钢梁截面的桥面段采用壳单元。由于箱型钢梁的内部设有很多纵向和横向的加筋肋,用壳单元进行网格划分时单元数目很多,进行动力响应计算工作量非常大,所以对桥面板进行等效模型的研究[9],推导出实心梁板和回字形梁板2种等效模型(以下简称为“实心模型”与“回字模型”)的各参数,从而为建模工作做准备。
2.1 基本参数
该博物馆折形人行吊桥的桥面是箱型钢构截面梁,其桥面梁板的横截面示意图如图2所示,各部分尺寸单位为mm。其中梁截面的总宽为B,厚度为H;梁外侧的2根纵向加劲肋的厚度为Bl1,梁中部3根纵向加劲肋的厚度为Bl2;从外向里各纵向加劲肋之间的距离分别为B1、B2、B3;梁高的空隙高度为H1。将箱型钢构截面梁等效成等厚度的实心钢梁,图3所示为等效桥面板的横截面尺寸,其中等效梁的宽度为Bd,厚度为Hd。由于桥面主要是以弯曲变形为主,为了保证等效桥面与箱型钢构截面梁桥面的力学性能尽可能一致,应保证两者的截面抗弯刚度、转动惯量和线密度相同。原桥面板内的横向加劲肋只设置在吊杆处,主要目的是防止桥面板被吊杆拉变形,质量相对总质量非常小,对桥面板横截面的抗弯刚度贡献很小,故在等效中未考虑横向加劲肋的影响。

图2 桥面板横截面图
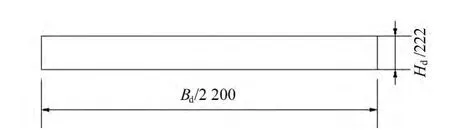
图3 实心桥面板横截面
2.2 抗弯刚度
梁截面的抗弯刚度为EI,其中I为截面绕中性轴的惯性矩。原结构桥面板的材质为钢材,弹性模量取值为E=2.1×1011Pa。根据惯性矩的等效可以确定等效桥面板的等效弹性模量Ed。原截面可以看成大矩形截面内存在几个小矩形截面的空隙。假定等效桥面的宽度Bd与原桥面宽度B相等,对等效实心模型来说,根据EI=EdId可以得到:
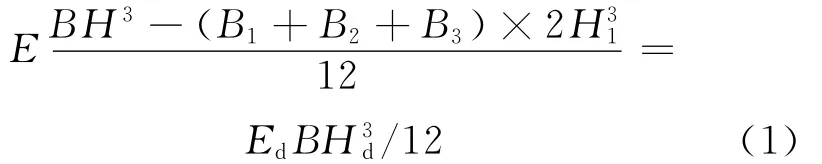
2.3 截面绕中性轴的转动惯量
根据动力学的知识,矩形截面梁绕z轴的转动惯量为:
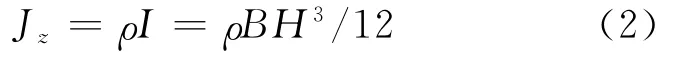
其中,ρ为材料的体密度;B、H分别为梁宽和梁高。对原桥面的钢材,计算中取ρ=7 850kg/m3。根据转动惯量的等效可以确定等效桥面板的等效高度,可以得到:
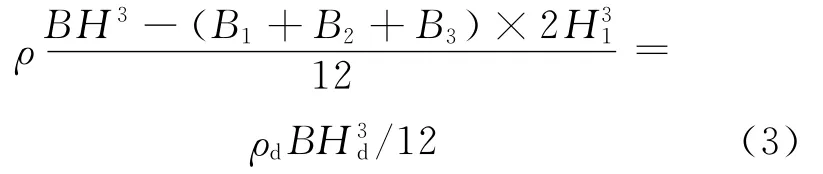
2.4 线密度
梁的线密度m等于材料的体密度与横截面积的乘积,即m=ρA。由于等效实心桥面板的截面尺寸发生了改变,为了保证等效模型与原模型的线密度相同,需要修改等效模型的体密度。原桥面板横截面大矩形面积为BH。空隙矩形截面的面积分别为B1H1、B2H1和B3H1。根据ρA=ρdAd可以得到

将(4)式代入(3)式即可确定等效实心模型的高度Hd,再将其结果代入(1)式和(4)式就能计算出等效模型的弹性模量Ed和体密度ρd。
2.5 模型参数确定
根据原桥面板截面的尺寸,B=Bd=2.2m,B1=0.24m,B2=0.265m,B3=0.505m,H=0.3m,H1=0.26m,再根据上述公式可以得出Hd=0.421m,ρd=1 142kg/m3,Ed=3.1×1010Pa。
2.6 回字形等效模型的参数确定
同样假设回字形等效桥面板的宽度与原桥面宽度相同,为保证抗弯刚度、转动惯量和线密度与原结构一致,可以将箱形梁内部的纵向加劲肋对称平移到最外侧。由此可以求出回字形模型的上下壁厚为0.02m,左右壁厚为0.09m,总高度为0.3m,弹性模量E=2.1×1011Pa,体密度ρ=7 850kg/m3。
3 有限元模型的建立
应用有限元分析软件ANSYS的前处理模块,建立原模型和2种等效模型的三维分析模型。模型中的桥面板和肋板采用SHELL63壳单元,吊杆采用LINK8杆单元,有限元分析的重点是结构的离散化。在建立等效模型时,假定等效桥面的宽度与原桥面相同,吊杆也固定在相同的位置,在对3种模型的桥面进行网格划分时都采用壳单元,且保持桥面板平面内单元的尺寸大小一致,使得计算结果具有可比性。原结构模型共划分113 955个单元,实心模型共划分15 898个单元,回字形模型共划分34 737个单元。原吊桥的整体有限元网格划分如图4所示。

图4 原吊桥ANSYS模型网格划分
4 模态分析
通过有限元软件ANSYS对原模型和2种等效模型进行模态分析,分别得到3种有限元模型的固有频率和振型图,通过对同一振型形态的固有频率对比判定等效效果的优劣。
通过ANSYS计算得到吊桥的前15阶的固有频率和振型。由振型图可知桥面极少发生侧向弯曲,所以只考虑桥面竖向弯曲,选取其中6阶主要振型进行比较,结果见表1所列。

表1 等效模型与原模型频率对比表 Hz
分析表1可以看出,等效模型与原模型的的固有频率计算结果比较接近,等效模型的计算结果相比于原模型普遍偏大,说明等效模型在等效过程中模型刚度得到了一定的加强。采用实心模型的最大误差为3.150%,回字模型的最大误差为4.523%,实心模型等效效果较好。由此可以证明,等效模型能够很好地模拟原模型的动力特性。
实心模型和原模型的一阶振型图分别如图5所示。
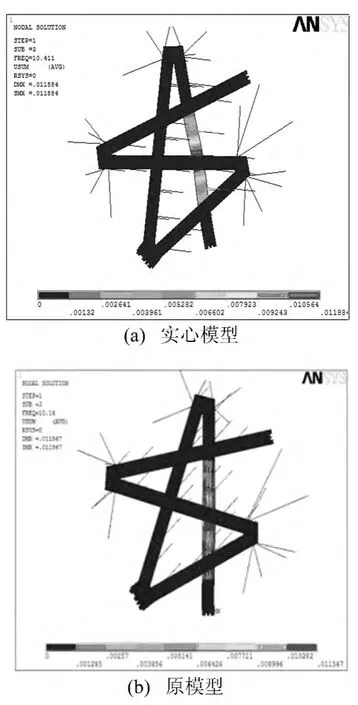
图5 实心模型、原模型一阶振型
5 行人荷载下动力响应的时程分析
行人激励引起的动力荷载并不像车道荷载一样只是一个固定大小的竖向移动荷载,而是一个相当复杂的过程。如何模拟行人荷载,即如何确定行人荷载的模式,一直是国内外学者关注的重点。总结国内外的研究成果可以发现,现今共有2种类型的荷载模式:时域内的荷载模式和频域内的荷载模式。本文使用英国规范BSI5400中规定的单个行人荷载模式来模拟行人引起的动力荷载作用,具体的荷载形式为:
其中,f0为行人步频,f0取2Hz;180为成人平均体重700N乘以Blanchard提出的荷载谐波因子0.257所得。取ξ=0.02,根据结构的前两阶固有频率计算瑞利阻尼。根据吊桥一阶竖弯振型图分别在吊桥的第1至第5层桥面的最大振型位移处设置荷载并布置测点,编号如图6所示。
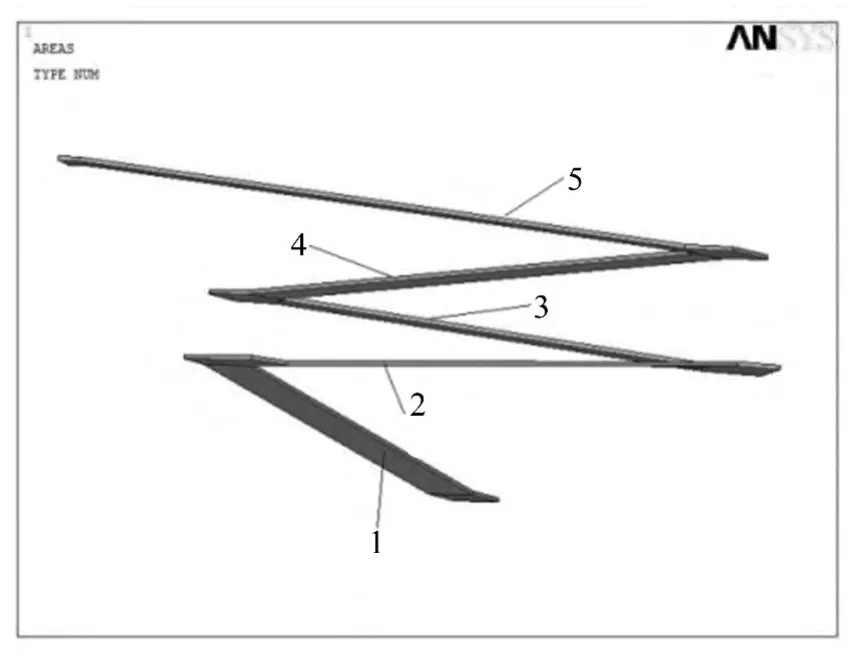
图6 吊桥测点位置编号
由于篇幅的原因,只给出1号测点加速度时程曲线的对比图,如图7所示,各测点的加速度峰值对比见表2所列。由图7和表2可以看出:实心模型和回字形模型的加速度峰值相差很小,原模型和等效模型的加速度曲线也能够较好地吻合,说明实心模型和回字模型的等效效果较好。

图7 吊桥1号测点加速度时程曲线对比图

表2 加速度峰值对比 mm/s2
6 结束语
本文利用等效方法建立了大型钢结构人行吊桥的2种等效模型,可以很方便地得到多肋桥面板的等效模型参数。应用有限元方法求解了吊桥3种模型的固有频率和振型,可以看出等效模型的固有频率比原模型有所增加,等效模型的整体刚度有所提高。实心模型与原模型的固有频率之间的误差相对较小,等效效果更好一些。计算结果表明,本文提出的等效模型是合理的,能很好地模拟原结构的整体动力特性。等效模型的建模工作量和计算工作量都大大减少了,尤其是模态分析和动力响应的时程分析效果更加明显。
[1] 杨亚政,杨嘉陵,曾 涛,等.轻质多孔材料研究进展[J].力学季刊,2007,28(4):503-516.
[2] 张广平,戴干策.复合材料蜂窝夹芯板及其应用[J].纤维复合材料,2000(2):25-27.
[3] 徐胜今,孔宪仁,王本利,等.正交异性蜂窝夹层板动、静力学问题的等效分析方法[J].复合材料学报,2000,17(3):92-95.
[4] 张广成,赵景利.蜂窝夹层结构复合材料的力学性能研究[J].机械科学与技术,2003,22(3):280-282.
[5] 周祝林,徐玉珍,孙佩琼.复合材料平板及蜂窝芯综合性能测试与分析[J].纤维复合材料,2002(4):17-20.
[6] 徐伟荣,牛 飞,盛宏玉.脱硫塔结构抗震分析中的简化模型研究 [J].合肥工业大学学报:自然科学版,2008,31(3):436-440.
[7] Soliman H E,Makhecha D P,Vasudeva S,et al.On the static analysis of sandwich panels with square honeycomb core[J].AIAA Journal,2008,46(3):627-634.
[8] 翟 光,杨小平,梁 斌,等.基于等效理论的多夹心层蜂窝板模态分析[J].机械强度,2007,29(3):517-520.
[9] 王文英,钱 怡.悬索桥等效模型的建立及讨论[J].路基工程,2007(5):28-29.

