基于健康指数的设备运行状态评价与预测

张彦如， 耿梦晓

（合肥工业大学 机械与汽车工程学院，安徽 合肥 230009）

0 引 言

随着现代化工业技术的蓬勃发展，制造企业内由设备安全性、稳定性、可靠性及运行效率等关键能力所确保的核心竞争力在竞争激烈的市场环境中显得尤为重要。确保设备可靠性和维护水平已成为保证系统正常运行的必要条件［1］。在实际生产过程中，随着设备使用寿命的增加，设备性能不断衰退，如不能对设备及时地进行维护，会使产品质量下降、生产周期延长，从而造成出货、交货延迟，顾客满意度下降［2］等问题，严重影响企业的生产效益。

在设备健康状态评价及预测的研究方面，20世纪90年代初期以来，美、英等国家对故障预测与健 康 管 理 （prognostics and health management，PHM）技术进行了大量的研究工作，已经从理论研究进入了实际的工程应用阶段，并渗透到了各个领域。文献［3］研究了应用专家系统评价变压器的绝缘状态；文献［4］将数据融合和数据挖掘技术相融合，全面评估设备的健康状态，并构造了一个在不同工业领域都能通用的状态维修体系。而我国在PHM方面的研究仍局限在航空航天领域，对于装配系统的健康管理研究不多。文献［5］提出的健康状态评价及预测方法基于多参数进行相关性分析，由相关性规律的变化判断发动机的性能；文献［6］提出在退化隐式马尔科夫模型的基础上引入老化因子的概念，描述设备性能的退化情况，用于诊断设备健康状态和预测有效剩余寿命；文献［7］在系统划分和状态特征参数提取的基础上，提出了基于模糊评判的发电设备状态综合评价方法；文献［8］提出了基于机械设备状态信息的运行可靠性评估方法，通过建立设备运行状态信息与可靠性之间的映射模型，实现运行可靠度的计算；文献［9］研究了对变压器运行状态进行模糊评价的多级评估方法，并综合得出变压器的运行状态。上述文献大多以单机设备的某关键特征参数为研究点，评价或预测该单一设备的运行状态，缺乏对系统内设备组综合运行状态的评价和预测研究。

由于装配系统由多台设备组成，因此本文建立了基于设备多特征参数健康状态的评价模型，以此为基础，构建设备综合健康指数，实现制造系统设备运行状态的量化表征，结合实际运行数据实时评价系统设备综合健康状态。此外，通过参数模型法拟合出设备综合健康指数随时间的变化趋势，预测设备的健康状态以及需要维护的时间节点，以实现对制造系统设备的综合健康管理，从而有效地提高制造系统的稳定性和可靠性。

1 设备综合状态评价与预测框架

健康状态是当前系统所处的状态，健康指数是与期望的正常性能状态相比较的性能下降或偏差程度，状态预测是根据系统现在或历史状态预测性地诊断系统未来的健康状态。要实现对装配系统设备综合健康状态评价与预测，需要评估系统设备当前的状态，并预测其未来状态以及设备失效时间。首先确定装配系统设备的监控部位和特征参数，然后以特征参数作为失效依据，运用参数检测法进行实时健康监测，得到健康指数用以判断设备的状态；其次通过参数模型法拟合健康指数随时间的变化趋势，得出未来某时刻系统健康参数的随机分布，并预测设备的健康状态和需要维护的时间节点。基于健康指数的设备综合运行状态评价与预测基本框架如图1所示。

图1 基于健康指数的设备综合运行状态评价与预测基本框架

2 单一设备健康状态评价模型

健康指数定义为设备在生产运行中保持特定性能的满意程度，是通过综合分析设备运行中各种状态信息和现场设备的运行工况得到的介于0和1之间的单一数值，其值越高表示设备的运行状态越好。1代表最佳状态，0代表完全失效状态。

2.1 单一设备单特征参数健康指数计算模型

设备在服役过程中，各指标的标准值随着时间不断发生变化。通过设备的设计参数和一定的历史统计数据，可以得到该参数的标准时间函数~fij（t）与该指标参数正常运行的最小极限值xmin和最大极限值xmax。

当实际测量值超过阈值范围时，健康指数为0，应立即停机检修；当实际测量值与标准值重合时，健康指数为1，为设备最佳状态；当实际测量值在阈值范围之间时，通过与标准值之间的距离相比较，可得出（0，1）之间的数值，用以量化设备状态，具体计算如下：

其中，hij（t）为基于设备i的单特征参数xj的健康指数；fij（t）为特征参数xj在t时刻的测量值；（t）为在t时刻该参数的标准值。

2.2 单一设备多特征参数健康指数计算模型

设备在运行过程中产生了丰富的状态信息，如噪音、应力、应变、温度、压力等，由于设备运行环境复杂，往往难以用设备单个状态特征参数的变化来评价整个设备的运行状态［10］。本文采用综合加权法对设备多特征参数健康状态进行评估，基于多状态特征参数的单一设备健康指数表达式如下：

其中，hi（t）为设备i基于多特征参数的健康指数；m为特征参数个数；ρij为特征参数xj的权重，反映了该参数对设备状态的影响，0≤ρij≤1，且＝1。

设备健康状态评价属于典型的多属性决策问题，设备i各特征参数权重ρij计算方法的确定是该类问题的核心。在设备健康状态评价中，当某些特征参数严重偏离正常值时，往往表示设备某部分性能已急剧下降，需加强监视甚至停机维护，但在常权评判模式中可能会因其权重较小，而整体评价还在正常范围，不能反映设备真实状态。故本文在对系统设备综合健康状态进行评价时，需要考虑各特征参数之间均衡性的问题，根据文献［11］提出的变权公式，可得到各监测特征参数权重的表达式如下：

其中，xij为系统中第i个设备的第j个特征参数；m为特征参数个数为特征参数xij的常权重；ρij为其变权重；α为常数，一般取值α＜1／2。

3 系统设备综合健康状态评价模型

系统设备由多个子设备构成，故对系统设备运行状态进行综合评价时，需要综合各个设备的健康状态。设备综合健康指数（health index，HI）定义为定量描述系统中设备综合运行状态介于0和1之间的单一数值。首先计算系统中各设备的健康指数，再根据各设备对系统运行状态的不同影响程度经过加权得到系统设备综合健康指数。

3.1 装配系统设备重要度评价

设备重要度是指从可靠性、经济性、维修性等因素出发，反映设备在系统正常运行过程中所处地位的重要性程度。设备重要度越高，说明设备对系统的整体运行影响越严重。重要度权重wi可采用层次分析法（AHP）加以确定。为了提高设备综合运行状态评价的可靠性，需要对不同设备进行重要度评价。评价指标体系如下：

（1）可靠性。指标包括对系统功能的影响程度、设备故障后的替代程度、对人员和环境安全性的影响及失效频率。

（2）经济性。指标包括设备原值、设备故障引起的损失费用及维修费用。

（3）维修性。指标包括维修的难易程度、备件的供应程度。

3.2 系统设备综合健康指数计算模型

基于多状态特征参数的设备综合健康指数HI（t）的表达式如下：

其中，HI（t）为基于设备状态的系统综合健康指数，HI（t）∈［0，1］；n为系统中设备数量。

系统设备综合健康指数HI（t）取值在0～1之间，但在工程实际中常用定性的方法将系统的健康状况划分为若干等级，如健康、比较健康、亚健康、不健康（轻微故障状态）、病态（故障状态）、严重病态（严重故障状态）。

依据企业实际生产经验数据，建立系统健康指数与运行状况定性评价等级之间的映射关系，将装配系统设备综合健康状况划分为6个等级，见表1所列。

表1 装配系统设备综合健康指数等级划分

4 系统设备综合健康状态预测

基于数据的预测技术不需要对象系统的先验知识（数学模型和专家经验）［12－14］，而是通过数据分析处理方法挖掘其中的隐含信息并进行预测。HI（t）是系统设备综合运行状态的量化表示，随着生产的进行，其变化呈现出复杂的非线性特征。健康指数时间序列反映了系统设备的宏观特征，同时也蕴涵着系统设备综合状态未来的演化信息。将健康指数HI（t）的历史数据通过回归分析，应用最小二乘法拟合出与历史数据最符合的曲线，通过曲线外推的方法进行系统设备综合健康情况预测，推断系统设备在未来某时刻的综合健康指数，并确定系统设备发生故障的概率以及需要维护的时间节点。

利用（4）式可求得在监测的t（t＝｛t1，t2，t3，…，tk｝）时间段内的系统设备综合健康指数HI（t），表达式如下：

设在t1时刻，系统的健康状态处于一级，即HI（t1）取1，随着生产的运行与时间的推移，健康指数逐渐下降；到tk时刻，系统健康状态处于四级，即该系统设备需要维护。建立相应的预测模型，预测系统需要维护的时间节点，提前制定相应的维护策略。

建立时间对系统设备综合健康指数影响的非线性模型。由于历史数据过多，通过实例验证需要五次多项式拟合才能够较好地反映时间与系统设备综合健康指数的关系。

故本文建立非线性模型，用公式表示如下：其中，β为拟合系数；t为监测时间。

高斯－牛顿迭代法收敛速度快、精确度高、残差小［14］。通过该方法求解上述非线性模型，得到拟合系数β，并以此预测系统设备未来时刻的综合运行状态，以便及时制定系统设备的维护策略。

5 实例验证

以安徽合肥某家汽车有限公司发动机装配车间为例进行设备综合健康状态评价与预测，参评设备包括拧紧机、涂胶机、压装机、翻转机、试漏机和冷试机。设备的综合状态评价分层次进行，如图2所示。首先计算各设备的健康指数，然后经过加权综合最终得到整个装配系统设备的综合健康指数。

根据现场测得的实时数据，拟合得到一段稳定时间内设备i的特征参数xj的时间函数fij（t）。提取出在t时刻各设备的特征参数，见表2所列。

对表2中的设备各特征参数，分别按（1）式计算得到在t时刻各设备的健康指数hij（t），计算结果也列于表2中。

由（4）式计算得到该系统设备综合健康指数HI（t）为：

由表1得到该系统设备运行状态为三级，即亚健康状态，出现异常征兆，不应长期连续运行。

通过系统设备综合健康指数历史数据，对设备在未来时刻的健康指数以及需要维护的时刻进行预测。连续采集该系统在正常运行状况下的200组原始数据为样本，采样间隔为10h，通过上述健康指数计算步骤，运用Matlab得出对应的设备健康指数样本数据拟合，如图3所示。

图2 发动机装配系统设备层次结构图

表2 装配系统各设备特征参数数值

由图3可以看出，观测时间在600h以内，设备综合健康指数急速下降，但仍属于比较健康的状态；随着设备运行时间的增长，设备综合健康指数变化不大，维持在一定水平；但当设备运行了1 800h后，设备综合健康指数又开始加速下降，步入亚健康状态。设备运行时间越久，相应的设备综合健康指数越小，从而进一步证明了本文所提出的发动机装配系统设备状态评价模型的有效性和实用性。

采用高斯－牛顿法，将系统设备综合健康指数历史数据代入，可以求得拟合系数β，见表3所列。表4所列为部分拟合残差，均小于－0.13，且随着设备运行时间的递增，残差值越小，说明拟合效果较好。

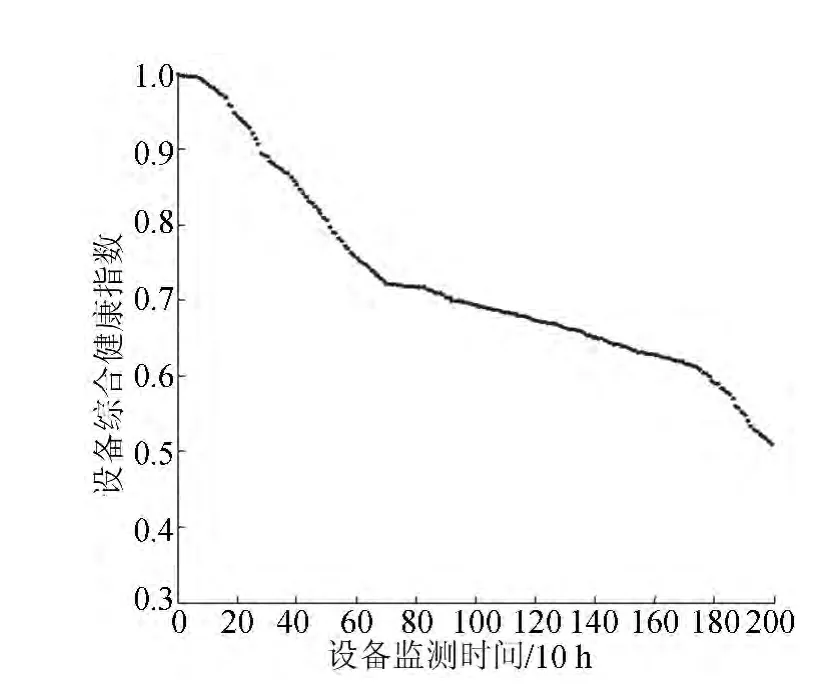
图3 设备健康指数样本数据拟合图

表3 高斯－牛顿法拟合结果

表4 拟合残差

根据求得的拟合系数，依据（6）式建立反映设备综合健康指数与时间的非线性表达式，即HI（t）＝1.0129 162 62＋（－0.022 329 93）t＋（－0.009 596 915）t2＋0.001 507 792t3＋（－7.862 33×10－5）t4＋（1.344 77×10－6）t5；令 HI（t）＝0.45，可求出t＝21.804 9，则需要在设备运行2 180h之后对该设备进行维护。经过现场的观察，系统内压装机设备在运行了2 300h的时候需要维护，证明了该预测模型的有效性。

6 结 论

（1）本文研究了装配系统的设备综合健康状态，建立了基于设备多特征参数健康状态评价模型，提出了设备综合健康指数的概念，实现了制造系统设备运行状态的量化表征，结合实际运行数据能够实时评价系统设备综合健康状态。

（2）通过设备历史数据建立预测模型，运用参数模型法拟合出设备综合健康指数随时间的变化趋势，预测设备的健康状态以及需要维护的时间节点，以便及时制定维护策略。

（3）实例分析表明本文建立的系统设备综合运行状态评价模型与预测模型有效可行，便于实现制造系统设备的综合健康管理，从而有效地提高制造系统的稳定性和可靠性，为生产现场的机械设备维护和诊断工作提供技术参考。

［1］ 廖雯竹.基于设备衰退机制的预知性维护策略及生产排程集成研究［D］.上海：上海交通大学，2011.

［2］ Pan Ershun，Liao Wenzhu，Zhuo Mingliang.Periodic preventive maintenance policy with infinite time and limit of reliability based on health index［J］.Journal of Shanghai Jiaotong University（Science），2010，15（2）：231－235.

［3］ Saha T K，Purkait P.Investigation of an expert system for the condition assessment of transformer insulation based on dielectric response measurements［J］.IEEE Transactions on Power Delivery，2004，19（3）：1127－1134.

［4］ Raheja D，Llinas J，Nagi R，et al.Data fusion／data mining－based architecture for condition－based maintenance［J］.International Journal of Production Research，2006，44（14）：2869－2887.

［5］ 李 强.民航发动机健康管理技术与方法研究［D］.南京：南京航空航天大学，2008.

［6］ 彭 颖.基于退化隐式半马尔科夫模型的设备健康预测及系统性维护策略研究［D］.上海：上海交通大学，2011.

［7］ 顾煜炯，董玉亮，杨 昆.基于模糊评判和RCM分析的发电设备状态综合评价［J］.中国电机工程学报，2004，24（6）：189－194.

［8］ 何正嘉，曹宏瑞，訾艳阳，等.机械设备运行可靠性评估的发展与思考［J］.机械工程学报，2014，50（2）：171－186.

［9］ 廖瑞金，王 谦，骆思佳，等.基于模糊综合评判的电力变压器运行状态评估模型［J］.电力系统自动化，2008，32（3）：70－75.

［10］ 宾光富，周 元.基于Fuzzy－AHP的机械设备多特征参数健康状态综合评价研究［J］.中国机械工程，2009（20）：2487－2492.

［11］ 骆思佳，廖瑞金，王有元，等.带变权的电力变压器状态

模糊综合评判［J］.高电压技术，2007，33（8）：106－110.

［12］ 胡舟宇.复杂成套设备关联建模技术及其应用研究［D］.杭州：浙江大学，2013.

［13］ 景 博，黄以锋，张建业.航空电子系统故障预测与健康管理技术现状与发展［J］.空军工程大学学报：自然科学版，2010，11（6）：1－6.

［14］ 杨兴明，陈海燕，王 刚.基于连分式的广义高斯分布的参数估计［J］.合肥工业大学学报：自然科学版，2012，35（7）：991－996.