非线性不确定多时滞切换奇异系统的鲁棒H∞保性能控制

张立俊，杨丽芸，刘春菊，仇计清，丛 悦，鲍冬冬

(1.河北科技大学理学院，河北石家庄 050018;2.石家庄铁道大学四方学院，河北石家庄050228)

切换系统是一类特殊的混杂系统，它是由若干子系统和描述它们之间联系的切换规则组成。根据恰当的切换规则可以使系统获得较好的性能，例如，2个不稳定的子系统可以通过适当的切换规则使得系统渐进稳定［1］。因为实际系统本身就包含了时滞和不确定性，而这些时滞和不确定性是造成系统不稳定的主要原因［2］。因此，人们对不确定时滞系统进行了广泛的研究［3-6］。在控制这一类系统的时候，人们希望既可以确保系统的稳定性，又可以获得一定的鲁棒性能。在这种研究背景下，文献［7］提出了保性能控制的思想，即设计一个控制器，使得该闭环系统对所有的不确定性，既保持鲁棒稳定性，又保证其给定的性能指标小于某一上界。对于保性能控制问题已经取得了丰富的研究成果［8-11］。文献［12］为了给不确定时滞系统设计鲁棒保性能控制器，提出了利用Riccati方程的方法。而文献［13］将最优保性能控制器的设计归结为具有LMIs约束的凸优化问题。

近几十年来，奇异系统已经被广泛地扩展到电力、经济等系统中，因为应用奇异模型描述问题来比其他系统模型更直接。因此，许多建立在奇异系统基础上的其他系统也得到了广泛的应用［14-16］，如基于线性矩阵不等式的奇异系统的鲁棒稳定性控制［17］，不确定时滞离散奇异系统的鲁棒H∞控制［18］等。但目前研究的切换奇异系统以不确定单时滞系统居多，而关于多时滞的研究尚不多见。本文研究了非线性不确定多时滞切换奇异系统的鲁棒H∞保性能控制问题。首先，定义鲁棒H∞保性能控制的定义;然后应用线性矩阵不等式LMIs的方法，根据相应的切换规则，设计鲁棒H∞保性能控制器，使得闭环系统符合鲁棒H∞保性能控制的定义，最后通过一个数值算例和仿真验证此方法的有效性。

1 问题描述和准备知识

考虑如下非线性不确定多时滞切换奇异系统:

其中:x(t)∈Rn，u(t)∈Rm，z(t)∈Rq和 ω(t)∈L2［0，+∞)分别表示状态，控制输入，被控输出和扰动输入向量，g(x(t))表示非线性干扰，且满足‖g(x(t))‖≤‖Mx(t)‖;φ(t)表示［－ξ，0］上连续的初始状态，h，d表示正的时滞常数，E∈Rn×n表示奇异矩阵，且满足 rank E=r＜n;δ(·):［0，+ ∞)→{1，2，…，n}def=表示分段常值切换信号，且 σ(t)=i表示第i个子系统在t时刻被激活。假设 Ai，Adi，B1i，B2i，Ci，Di，Gi，M表示系统具有适当维数的常矩阵，ΔAi，ΔAdi表示描述参数不确定性的不变矩阵，且具有如下形式:

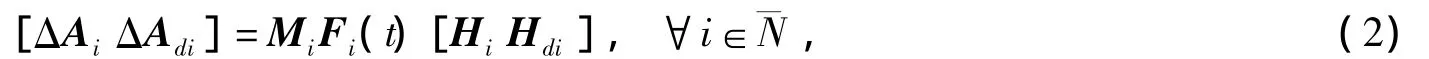
其中Mi，Hi，Hdi(i∈)表示给定的具有相应维数的常矩阵。Fi(t)表示不确定矩阵，且满足(t)Fi(t)≤I。

定义1 考虑系统(1)的自由系统如下:

1)对每一个i∈M，存在s∈C，使得det(sE－Ai－Adi)≠0，则称切换奇异系统(3)是正则的;

2)如果系统(3)是正则的，对所有s∈C，均满足deg(det(sE －Ai－Adi))=rank E，i∈M，deg(p(s))表示多项式p(s)的次数，则称切换奇异系统(3)是无脉冲的。

注1:文中所研究的切换奇异系统均是正则和无脉冲的。证明过程可以参见文献［17］。

注2:M表示一个有限的整数范围，C表示全体实数。

为了方便对问题的研究，x(t)，x(t－d)，x(t－h)，ω(t)，g(x(t))分别被记为 x，xd，xh，ω，g，且

系统(1)在状态反馈控制器uδ(t)(t)=Kδ(t)x(t)作用下的闭环系统为

引入性能指标:

其中Q和R是给定的正定加权矩阵。

定义2 对于系统(1)和给定的常数γ＞0，设计切换规则σ(t)，如果对于所有的参数和性能指标(5)，使得到的闭环奇异切换系统(4)满足:

1)当ω(t)≡0时，闭环奇异切换系统(4)的零解是渐近稳定的;

2)当 φ (t)=0 时，对任意非零向量 ω (t)∈L2［0，+∞)，满足 ‖z‖［0，+∞)＜γ2‖ω‖［0，+∞)成立;

3)存在性能指标的一个上界J*＞0，使得闭环系统(4)是渐进稳定的，且满足J≤J*。则称状态反馈控制律uδ(t)为系统(1)的鲁棒H∞保性能控制律。

引理1［14］(schur补引理)若已知3个矩阵和Ω1，Ω2和Ω3，则＜0，当且仅当

引理2［15］对于任意给定的适当维数的矩阵X，Y和任意标量α＞0，有:

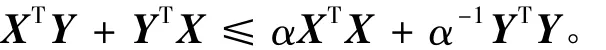
引理3［16］对于适当维数的矩阵Y，M，H，则Y+MFH+HTFTMT＜0，对于所有满足FTF≤I的矩阵成立，当且仅当存在标量ε＞0，有:

2 主要结果

定理1 对于给定的常数γ＞0，λ＞0和性能指标(5)，若存在可逆对称矩阵P∈Rn×n，矩阵Ki及对称正定矩阵 Q1，Q2，n个满足的实数αi，使得如下矩阵不等式成立:

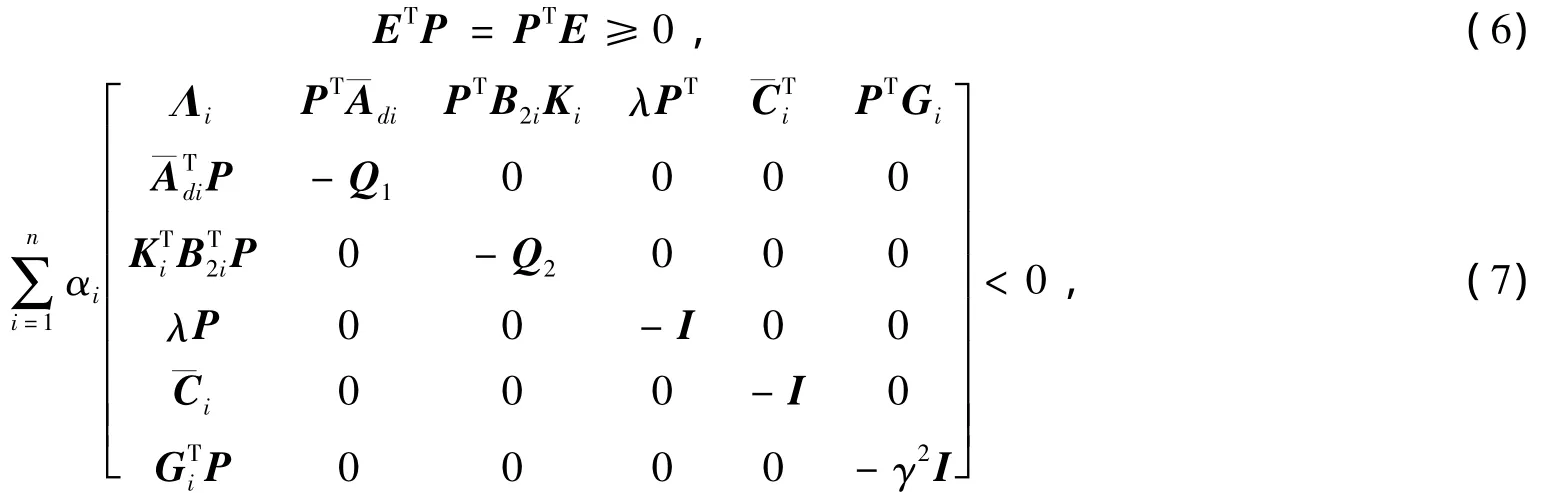
则系统(1)是具有鲁棒H∞干扰抑制水平γ状态反馈可切换正定的。其中=Kix(t)是系统(1)的一个鲁棒H∞保性能控制律，且相应的性能指标满足:

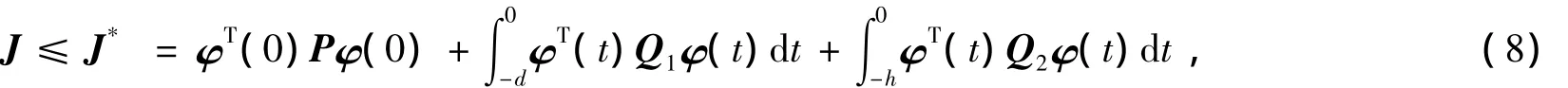
选取的切换规则为

证明 由引理1，不等式(7)等价于

即对于∀x∈Rn/{0}，有:

假设{(tk，ik)，0=t0≤t1≤…}是由切换规则(9)在区间［0，+∞)上生成的切换序列，其中(tk，ik)表示当tk≤t≤tk+1第ik个子系统被激活且在tk+1时离开。对闭环系统(4)构造Lyapunov函数V(xt)，使得对任意非零状态x，V(xt)是正定的。令

V(xt)沿闭环系统(4)对t求导，可得:

首先证明当ω(t)=0时，闭环系统(4)在切换规则(9)下的零解是渐进稳定的。

当ω(t)=0时，

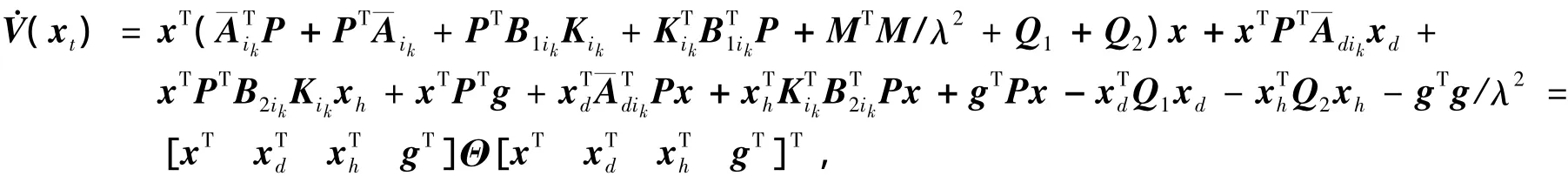
结合式(7)和式(12)可得:

由Lyapunov稳定性理论，闭环系统(4)在切换规则(9)下的零解是渐进稳定的。

下面证明闭环系统(4)满足给定的H∞性能指标。

由引理2知:

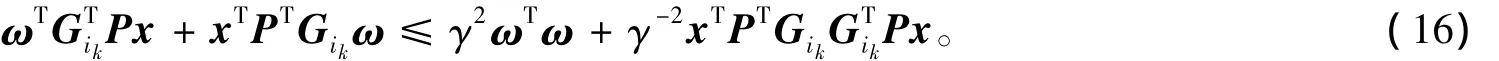
对于任意的ω(t)∈L2［0，+∞)，结合式(14)和式(16)，可得:

其中:

故，

当φ(t)=0时，式(17)两边分别从0～+∞ 对t积分，可得:

故，对于任意的 ω (t)∈L2［0，+∞)，有‖z‖［0，+∞)＜γ2‖ω‖［0，+∞)。

将式(15)两边分别对tk从0～+∞ 取积分，可得:

由此定理得证。

定理2 满足定理1条件，式(6)与式(7)的充要条件为对于任意给定的正实数γ＞0，常数λ＞0，若存在 非 奇异可逆矩阵 S ∈Rn×n，ε＞0，及对阵正定矩阵 Ki，X，Y，常数 ε＞0，n个满足 αi＞0，i∈，且的实数αi，使得如下矩阵不等式成立:

此时，

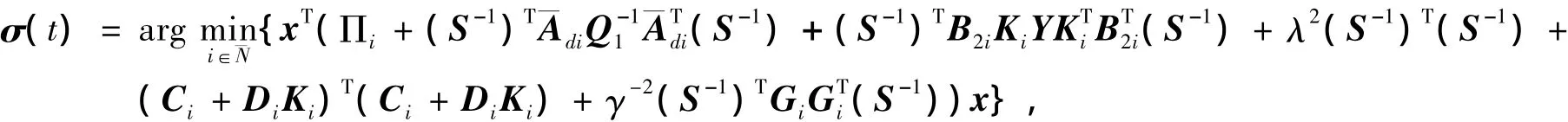
证明 根据定理1只需要证明式(6)和式(7)分别与式(20)和式(21)等价即可。

在式(7)中，分别用Ai+ΔAi(t)=Ai+MiFi(t)Hi，Adi+ΔAdi(t)=Adi+MiFi(t)Hdi，Ci+DiKi代替，可以得到下面的式子:

由引理3，式(22)成立时，当且仅当

成立。

对式(23)应用引理1，并且左乘 d iag{P－1，I，I，I，I，I，I，I，I，I}T右乘 d iag{I，I，I，I，I，I}，并令 P－1=Ti，则可推导出式(21)与式(7)等价。

另外，令P－1=X，容易得出式(20)与式(6)等价。故定理2得证。

定理3 对于系统(1)和性能指标(5)，对于给定的常数γ＞0，λ ＞0，如果存在可逆矩阵S∈Rn×n，ε＞0，β＞0，及对阵正定矩阵 X ，Y，N1，N2，n个满足 αi＞0，i∈，且的实数αi，使得以下凸优化问题有最优解

证明 由定理2知，若式(21)成立，则Uδ(t)(t)=Kδ(t)x(t)=Tδ(t)P为系统(4)的鲁棒H∞保性能控制器，性能指标上界由式(19)确定。

式(24)中的2)等价于 φT(0)S－1φ(0)＜β，

式(24)中的3)等价于UTX－1U＜N1，且tr{UTX－1U}＜tr{N1}，

式(24)中的4)等价于UTY－1U＜N2，且tr{UTY－1U}＜tr{N2}。

3 数值举例

考虑如下非线性不确定多时滞切换奇异系统(1)的参数如下:

选取 γ =1，λ = 0.3，ξ=1，性能指标的对称加权矩阵为初始条件为

通过应用LMIs工具箱中的mincx，得到:

利用这个可行解构造出该系统的最优鲁棒H∞保性能控制器:

相应的性能指标J*=23.905 5。

4 结语

本文针对一类非线性不确定多时滞切换奇异系统，研究了该系统的鲁棒H∞保性能控制问题。主要目的是给出鲁棒H∞保性能控制器，该控制器不仅使得闭环系统是渐进稳定的，而且相应的性能指标不得超过某个规定的上界。基于Lyapunov函数和线性矩阵不等式，得到闭环系统渐进稳定的充分条件并设计鲁棒H∞控制器。最后通过数值举例证明了所用方法的有效性。

/References:

［1］ LIBERZON D，MORSE A S.Basic problems in stability and design ofswitched systems［J］.IEEEControl SystemsMagazine，1999，19(5):59-70.

［2］ 宋正一，赵军.不确定时滞线性离散切换系统的鲁棒H∞控制［J］.自动化学报，2006，32(5):760-766.SONG Zhengyi，ZHAO Jun.RobustH∞control for linear deiscrete-time switched systemswith norm-bounded uncertainties and time-delay［J］.Acta Automatica Sinica，2006，32(5):760-766.

［3］ 王刻奇，杨智.不确定离散时滞系统的时滞相关保性能控制［J］.信息与控制，2010，39(3):373-378.WANG Keqi，YANG Zhi.Delay-dependent guaranteed cost control of uncertain discrete time-delay system［J］.Information and Control，2010，39(3):373-378.

［4］ CHENWuhua，GUAN Zhihong，LU Xiaomei.Delay-dependent guaranteed cost control for uncertain discrete-time systemswith both state and input delays［J］.Journal of The Franklin Institute，2004，341(5):419-430.

［5］ 邱占芝，张庆灵，刘明.不确定时延输出反馈网络化系统保性能控制［J］.控制理论与应用，2007，24(2):274-278.QIU Zhanzhi，ZHANG Qingling，LIUMing.Guaranteed performance control for output feedback networked control systemswith uncertain time-delay［J］.Control Theory ＆ Applications，2007，24(2):274-278.

［6］ 孙晓岭，杨丽芸，鲍冬冬，等.时滞网络化控制系统的鲁棒H∞稳定性分析［J］.河北科技大学学报，2013，34(4):297-301.SUN Xiaoling，YANG Liyun，BAODongdong，et al.Analysis of robustH∞stability for time delay network control system［J］.Journal of Hebei University of Science and Technology，2013，34(4):297-301.

［7］ SHEKDIN SL，PENG T K C.Adaptive guaranteed cost control of systemswith uncertain parameters［J］.IEEE Transactionson Automatic Control，1972，17(4):474-483.

［8］ YONEYAMA J.Robust stabilization for uncertain time-delay systems under time-varying sampling ［J］.Applied Mathematical Sciences，2009，38(3):1873-1883.

［9］ JIA Huimei，XIANG Zhengrong，KARIMIH R.Robust reliable passive control of uncertain stochastic switched time-delay systems［J］.Applied Mathematics and Computation，2014，231:254-267.

［10］ DU Zhaoping，ZHANGQinglin.Delay-dependent robustcontrol for uncertain singular systemswithmultiple state delays［J］.IETControl Theory Application，2009，3(6):731-740.

［11］ 何召兰，高岑，武俊峰.不确定时滞切换奇异系统的鲁棒H∞控制［J］.北京化工大学学报(自然科学版)，2012，39(1):89-92.HE Zhaolan，GAO Cen，WU Junfeng.RobustH∞control for uncertain time-delay switched singular systems［J］.Journal of Beijing University of Chemical Technology(Natural Science)，2012，39(1):89-92.

［12］ MAHMOUD M S，XIE L.Guaranteed cost control of uncertain discrete systemswith delay［J］.International Journal of Control，2000，73(2)，105-114.

［13］ 杨坤，沈艳霞，纪志成.不确定时变时滞切换奇异切换广义系统的鲁棒H∞保性能控制［J］.控制决策，2013，28(5):787-796.YANG Kun，SHEN Yanxia，JIZhicheng.RobustH∞guaranteed cost control for uncertain switched singular systems with time-varying delay［J］.Control and Decision，2013，28(5):787-796.

［14］ YUE D，HAN Q L.Delay-dependent exponential stability of stochastic systems with time-varying delay nonlinearity and markovian switching［J］.IEEE Transactions on Automatic Control，2005，50(2):217-222.

［15］ SU H，WANG X Z.Flocking formulti-agents with a virtual leader［J］.IEEE Transctions on Automatic Control，2009，54(2):293-307.

［16］ XU Shengyuan，SHIPeng，CHU Yuming，et al.Robust stochastic stabilization andH∞control of uncertain neutral stochastic time-delay systems［J］.Journal of Mathematical Analusis and Applications，2006，314(1):1-16.

［17］ WU Zhengguang，ZHOUWuneng.Delay-dependent robust stabilization for uncertain singular systemswith state delay［J］.Acta Automatica Sinica，2007，33(7):714-718.

［18］ FANG Mei.Delay-dependent robustH∞control for uncertain singular systemswith state delay［J］.Acta Automatica Sinica，2009，35(1):65-70.