岩石三点弯曲梁破坏过程数值模拟研究
刘 松,周宗红,付 斌,肖迎春(昆明理工大学国土资源工程学院,云南 昆明 650093)
岩石三点弯曲梁破坏过程数值模拟研究
刘 松,周宗红,付 斌,肖迎春
(昆明理工大学国土资源工程学院,云南 昆明 650093)
【摘 要】本文选用能够分析真实破裂过程的数值模拟工具RFPA2D,针对岩石试样三点弯曲梁的破坏过程进行数值模拟及分析,研究了加载不同位移量的破坏规律和偏置裂纹的位置对三点弯曲梁破坏模式的影响。数值模拟结果表明:在加载位移量小时,三点弯曲梁发生拉伸破坏,且只出现一条裂纹;在较大的加载位移量时出现多条平行拉伸裂纹;当L<3cm时,偏置裂纹尖端首先起裂,并向上扩展贯通整个试样的高度;当L≥3cm时,伴随偏置裂纹发育的同时,梁底部中心位置也出现了一条中心裂纹,然而最终仅中心裂纹贯通了整个试件。由于岩石自身存在非均匀性,局部的裂纹发育情况呈现出曲折性。破裂模式上模拟结果与相关的试验结果具有较好一致性。
【关键词】三点弯曲;RFPA2D;岩石破裂;数值模拟;裂纹扩展;偏置裂纹
1 引言
1.1研究现状
岩石自身的强度及其含有的微裂纹决定了岩石类材料的断裂过程,而其破坏过程实际上就是微裂纹萌生、扩展、贯通,直至岩石破裂失稳的过程,裂纹断裂路径的发育情况对于岩体工程设计有着十分重要的意义。岩石材料自身所具有的非均匀性,使其断裂破坏过程变得十分复杂,如何分析这种复杂的断裂破坏失稳过程,一直是学者们的研究重点[1-2]。很多国内外学者针对裂纹扩展及其所导致的岩体破坏过程,进行了大量的科学试验研究[3-4]。在岩石断裂力学的研究过程中,鉴于三点弯曲试件试验简单,故使用较多,但断裂力学的理论还是建立在假设材料均匀的基础之上,很多岩石的破坏过程数值模拟工作还是停留在宏观研究上,且假设岩石是一种均匀材料,没有给出岩石破裂的整个过程及其特征。
1.2RFPA2D软件简介
在模拟岩石类的破坏过程方面,RFPA(Rock Failure Process Analysis)程序具有很强的适应性。RFPA系统基于岩石细观结构的认识,首先把材料离散成具有一定尺寸的细观基元,认为材料宏观破坏是细观单元破坏的累积过程。从细观力学角度考虑,认为构成岩石类材料的每个微观单元是均匀且连续的介质,但是这些单元之间的力学性质(如强度、弹性模量等)可能相差很大,包含缺陷多的微观单元间则表现出更大的离散性。用RFPA2D进行三点弯曲变形与破坏过程的数值模拟不但可以得到每一加载步的应力场以及声发示意图,还可以通过图形显示模型从裂纹萌生扩展直至贯通的整个过程。该程序能够很好地模拟岩石的破坏模式以及破坏过程中声发射分布,故已大量应用于岩石破裂机制和岩石力学与工程问题的研究中,并已取得了重要的研究成果[5-8]。
应用RFPA系统通过加载不同位移量,模拟岩石试样在三点弯曲试验中试件宏观破坏过程中裂纹的发育规律,再现试样载荷后的裂纹萌生、扩展直至断裂的全过程,从细观力学角度对岩石试件的破坏过程进行模拟研究;并且对含偏置裂纹的三点弯曲梁在荷载作用下的破坏过程进行模拟,通过对比分析得出荷载作用下含偏置裂纹三点弯曲梁的断裂机制。
2 数值模型及方案
数值模拟中采用的试件尺寸[9]为120mm×40mm(长×高),跨度为100mm,在跨度中间作用有集中载荷P,单元的规模为240×120=28800个单元。模拟中的试件分两组:a组为无预制裂纹组,共有2个试件,编号为a1、a2;b组为有预制裂纹组,根据断裂力学的试验方法,试样中会预制初始裂纹,从而保证在初始裂纹处开始断裂扩展。预制裂纹的位置用L来表达,共有5个试件,L为试件下部的预制裂纹到跨中的距离,在L分别取0、1、2、3、4cm处分别开切一个长10mm、宽1mm的预制裂纹。数值模型的详细情况如图1,图中以不同灰度表示弹性模量。
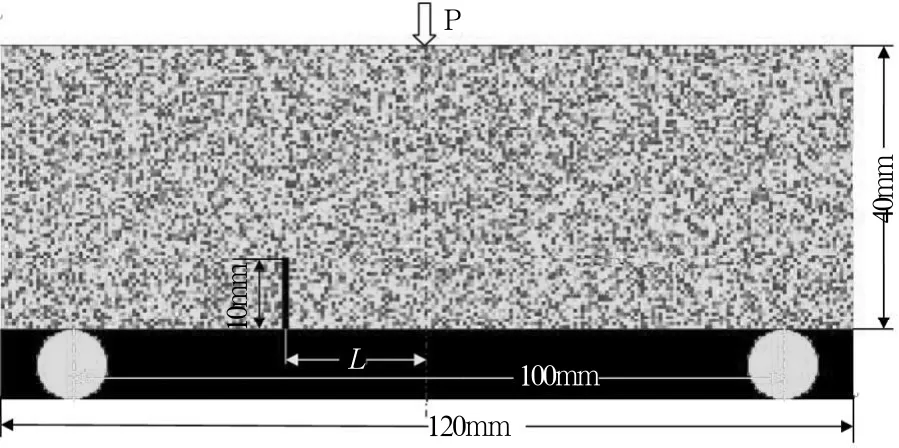
图1 三点弯曲数值模型
在模拟中把模型简化为平面应力问题来研究,假设试样为非均匀材料,其细观力学参数按Weibull分布随机赋值,且由相同尺寸的四边形单元构成。试验的相变控制参数取值如下:内摩擦角30°,压拉比为10,最大压拉应变系数分别为200和1.5,残余强度阈值系数为0.1,采用修正的Coulomb准则作为判断依据。
三点弯曲梁材料力学性质参数为:均质度1.5、抗压强度55.8MPa、弹性模量56.5GPa、泊松比0.28、摩擦角30°、密度2770kg/m3。每组试验均采用相同的力学参数。每个试件的加载方式均采用位移控制的分布加载,a组试件每一步的加载位移量分别为0.001、0.002mm,b组试件每步的加载位移量为0.001mm。
3 数值模拟结果分析
3.1a组试件模拟结果分析
(1)a1试件每一步的加载位移量为0.001mm,一共加载了100步。图2给出了试件模拟全过程的应力—加载步曲线。
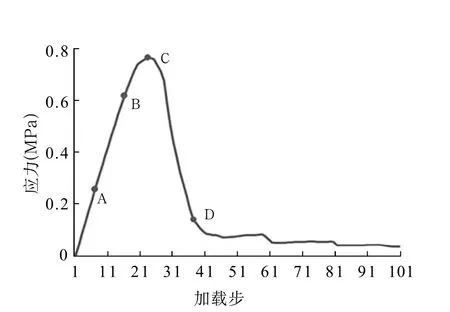
图2 应力—加载步曲线
从图2中可以看到,当加载到第10步(图2中的点A)时,此时应力达到0.38MPa,试样在底部中央开始产生破裂点,此后随着加载步的不断增大,破裂点逐渐增加且增加的速度越来越快。当加载到第20步(图2中的点B)时,试件底部中间偏左位置出现明显裂纹并伴有次生裂纹出现。当加载到第23步(图2中的点C)时,所承受的应力达到了峰值,此时在梁的底部跨中位置产生了较多破裂点,梁的底部萌生一组垂直横梁方向的微裂纹(如图3中step23所示),受拉破裂点数目持续增加并且开始在梁的中部大量聚集,逐渐向加载点一侧靠近,这是由于三点弯曲试验中梁的中间部位所受应力最大,并以纯拉应力为主。在此之前,试件一直表现出较好的线性(图2中AC段)。继续加载,由于裂纹尖端高度应力集中,主要裂纹与次生裂纹开始由各个微裂纹贯通产生,并且主要裂纹与次生裂纹基本平行,试件的承载力开始迅速下降且表现出材料的非线性特征(图2中CD段),当加载到第28步时,裂纹的扩展长度大约是梁高的1/2,并且向着加载点方向继续扩展,从图3中可以看出当加载到第62步时,破裂点数目几乎不再增加,此时破裂点在试件中间偏左位置形成了一条断裂带,裂纹贯穿试件,并且试件的承载能力几乎为零,试件彻底破坏。
图3是三点弯曲梁破裂全过程图,图中给出关键步的最大主应力示意图。为了观察方便,其中主应力图是试件的某一固定截面图,可以清楚地观察到模型内部的裂纹发展状况。
从图3中可知,模拟开始加载时试件加载点受压应力作用,并且在加载点附近产生压应力集中,试件下部中心位置附近受分布较分散的拉应力作用,在两个支点位置附近没有拉应力集中。在外荷载作用下,受拉区内低强度基元首先破坏,相互贯穿产生多条微裂纹破坏,这些微裂纹方向垂直于受拉方向,但是并不是所有的裂纹均进一步发育破坏。这些微裂纹在荷载的作用下继续萌生,并随着载荷的增加逐渐发育、贯通,形成主要的破坏裂纹。随着荷载的增加,试样很快就会达到抗拉强度极限而发生破坏,而此时受压区内大部分单元并没有发生破坏,这是因为岩石的抗拉强度远小于其抗压强度。而后受压单元回弹卸荷,导致试样承载能力快速降低,释放出的能量致使试件宏观破坏。破坏过程中的裂纹并不是始终沿着垂直方向,局部的裂纹扩展呈现出曲折性。说明岩石自身的非均匀性对裂纹起裂的部位和局部的发育路径有很大影响,但是试件裂纹的发育路径总体上有一定的规律。
(2)a2每一步的加载位移量为0.002mm,共加载了50步。出现了另一种破裂模式,如图4所示。当对试件加载不同的位移量时,试件的破坏表现出一定的规律性。载荷加载到试样上,试样中部分分散的强度低的单元荷载先达到阀值,发生了零星的破坏。在梁的下部中心位置分散的破坏单元连接、贯通、聚集形成规模很小的数条微裂纹,其中有3条微小的平行裂纹(如图4中step12)可见。随着继续加载,试件下边缘的3条裂纹中的两边裂纹继续由下向上扩展发育为主要裂纹,并伴有分叉的剪切裂纹出现,而中间裂纹不在扩展发育(如图4中step20)。从细观上来看,其破坏主要是由于拉伸损伤造成的受拉破坏,破裂点数目持续增加并且开始在梁的中部大量聚集,逐渐向加载点一侧靠近,拉应力集中转移到新的裂纹尖端,裂纹尖端的拉应力正是促使裂纹扩展的因素。继续加载,生成的两条主要裂纹扩展到一定阶段后右侧裂纹停止发育,而原有的左侧裂纹向着加载端方向继续扩展。最终试样内出现2条规模较大的裂纹,左侧裂纹贯通整个试样,右侧裂纹长度大于试样高的一半(如图4中step36)。

图3 a1试件断裂过程

图4 a2试件断裂过程
(3)在加载的位移量小时,在试样中间形成一条拉伸裂纹,加大位移量时形成了既有拉伸裂纹又有剪切裂纹的数条裂纹。从图3可以看出加载位移量为0.001mm时,在试件的底部首先出现单元的破坏现象,并且下部形成初始微裂纹并且逐渐的扩展成主要裂纹,随着不断加载,试件的下部又生成了新的次生裂纹,模拟过程中试样破坏的规模小,裂纹贯通的速率也慢。当位移量上升到0.002mm/步时,破坏单元还是出现在试件的下部,与a1试样相比,a2试样单元破坏的时间提早,而且单元破坏时释放的能量、数量、增长的速度都很高,单元破坏到一定程度时,试件下部靠近中心位置形成3条规模很小的初始微裂纹,但是继续加载后,中间的初始裂纹不再发育,左侧和右侧的初始裂纹扩展的速度较快,最终左侧初始裂纹扩展成为主裂纹,贯通整个梁。而另一条初始裂纹的扩展速度相对较慢,最后不再扩展,其裂纹数量和裂纹扩展规模都明显要高于位移量为0.001mm的情况。在两种加载位移量情况下,三点弯曲梁达到最大承载力后并没有立即失稳破坏,其承载力是逐渐下降的,即该岩石材料没有显示出明显的脆断性。
3.2b组试件模拟结果分析
b组加载位移量为0.001mm,共加载50步。通过多次模拟,研究了L的不同取值对梁破坏模式的影响。随着L慢慢加大,试样底面的中心裂纹起裂的时间会推后。开始加载时起裂较缓慢,随后扩展速度逐渐加快。当L=0、1、2cm时,新裂纹在预制裂纹尖端处起裂,进而向着加载点的方向缓慢扩展、发育,最终贯穿整个试样。当L=3、4cm时,预制裂纹尖端处与试样下端面的中心位置同时开始萌生新的裂纹,随后预制裂纹处的裂纹停止发育,中心裂纹继续向上贯通,最后导致试件破坏,失去承载力。在破裂模式上,数值模拟结果与相关试验结果[10-13]具有较好的一致性。
经过多次的数值模拟得到了两种典型的破坏模式,下面分别以L=2cm和L=3cm时的两种破坏模式为例加以介绍。图5给出了L=2cm时梁的最大主应力分布图。施加荷载后,辐射状的应力向加载点下部传播,在试件中产生了复杂的分布形态。到达预制裂纹的尖端处时,发生应力集中现象。在第8步时,预制裂纹尖端处出现了新的微裂纹,新裂纹向着试样上部加载点的方向发育,最后贯通试样。图6给出了L=3cm时破坏模式图,开始加载时,试样中的应力分布与图5中的现象相像。但是新裂纹的起裂时间要推后,在偏置裂纹的上端首先起裂,随后,在试样的下部中心位置也出现新的裂纹。但是偏置裂纹处的新裂纹在35步后就不再发育,中心处裂纹扩展的速率加快。最终是中心处的主裂纹贯通了整个试样高度,致使三点弯曲试样宏观破裂。
数值模拟结果表明:L=3cm是试验破坏模式不同的转折点;当L<3cm时,偏置裂纹处产生新裂纹,并向着加载点的方向贯通试件;当L≥3cm时,偏置裂纹处率先产生新裂纹,随后试件底部中心附近发育出新裂纹,但只有中心主裂纹最后贯穿试件,致使试件完全破坏。

图5 L=2cm时梁的破坏过程

图6 L=3cm时梁的破坏过程
4 结论
本文数值模拟了施加不同位移量作用下的岩石三点弯曲试件的破坏规律,在加载作用下,裂纹的数量受加载位移量的影响而不同;并且模拟了含有偏置裂纹的试样破坏过程及模式,探讨了偏置裂纹的不同位置对其破坏模式的影响。主要结论如下:
(1)在低位移量加载情况下形成一条跨中部位的拉伸裂纹; 在较大加载位移量情况下,形成多条平行拉伸裂纹,部分拉伸裂纹分叉形成剪切裂纹。
(2)在较大的加载位移量下,单元破坏的时间提早,而且单元破坏时释放的能量、数量、增长的速度都很高。
(3)三点弯曲梁达到最大承载力后并没有立即失稳破坏,其承载力是逐渐下降的,即该岩石材料没有显示出明显的脆断性。
(4)随着距离L的增大,偏置裂纹的发育时间推迟。当 L<3cm时,新裂纹在偏置裂纹处发育,并向上扩展贯通整个试样;当L≥3cm时,偏置裂纹处率先产生新裂纹,随后试件底部中心附近发育出新裂纹,但只有中心主裂纹最后贯穿试件,致使试件完全破坏。
【参考文献】
[1]管辉,黄炳香,冯峰.灰岩试样三点弯曲断裂特性试验[J].煤炭科学技术,2012,40(7):5-9.
[2]左建平,柴能斌,周宏伟.不同深度玄武岩的三点弯曲细观破坏实验研究[J].岩石力学与工程学报,2013,32(4):659-695.
[3]吴刚,翟松韬,李玉寿,等.高温下大理岩受压破坏的细观结构分析[J].岩石力学与工程学报,2012,31(2):3579-3585.
[4]左建平,黄亚明,刘连峰.含偏置缺口玄武岩原位三点弯曲细观断裂研究[J].岩石力学与工程学报,2013,32(4):740-746.
[5]ZUO J P, XIE H P, ZHOU H W. Investigation on meso-failure behavior of sandstone under thermal-mechanical effects based on high temperature SEM[J]. Science China Physics, Mechanics and Astronomy, 2012, 55(10): 1855-1862.
[6]马悦,戴峰,徐奴文,等.观音岩水电站混凝土梁三点弯曲试验的数值模拟[J].混凝土,2015(4):14-17.
[7]刘松,周宗红,肖迎春,等.石灰岩抗拉强度的试样厚度效应试验研究[J].中国钨业,2015,30(2):7-11.
[8]钟惠萍,黄小明,张建仁,等.混凝土拉伸断裂过程的RFPA2D模拟[J].长沙交通学院学报,2001,17(2):49-53.
[9]中华人民共和国国土资源部.DZ/T0276.22-2015岩石物理力学性质试验规程(第22部分):岩石抗折强度试验[S].北京:中国标准出版社,2015.
[10]赵小平,左建平,裴建良.锦屏层状大理岩断裂机制的细观试验研究[J].岩石力学与工程学报,2012,31(3):534-542.
[11]左建平,周宏伟,范雄,等.三点弯曲下热处理北山花岗岩的断裂特性研究[J].岩石力学与工程学报,2013,32(12):2422-2430.
[12]XIE H P, ZUO J P, ZHOU H W, et al. Meso-failure mechanism of rock under thermal-mechanical coupling effects[J]. Journal of Mechanics and MEMS, 2009, 1(2): 157-167.
[13]贾敬辉,张永彬.动荷载作用下三点弯曲梁的破坏形式与偏置裂纹位置的关系[J].武汉理工大学学报,2012,34(11):84-87.
Numerical Simulation of Failure Process of the Rock Three Point Bending Beam
LIU Song, ZHOU Zong-hong, FU Bin, XIAO Ying-chun
(Faculty of Land Resources Engineering, Kunming University of Science and Technology, Kunming 650093, China)
Abstract:In this paper, the real failure process analysis simulation tool RFPA2Dwas used to simulate the damage process of rock sample three-point bending beams. The failure law of the different displacement and the influence of the position of the offset notch on the failure mode of the three point bending beam is studied. Numerical simulation results show that, when the load displacement amount is small, three-point bending beam tensile failure occur, and appeared only one crack; when a large amount of load displacement, a plurality of parallel tension cracks occur; when L< 3cm, offset notch tip first initiation and upward expansion along a certain angle. and then ultimately through the entire height of the sample; when L≥3cm, offset notch expansion occurs, at the same time, in the bottom center of the beam position is also sprouted out of a central crack, but in the end only the central crack through the entire height of the sample. Due to the heterogeneity of the rock itself, partial crack propagation is tortuous. The numerical simulation results are in good agreement with the experimental results.
Key words:three-point bending; RFPA2D; rock failure; numerical simulation; crack propagation; offset notch
【收稿日期】2015-08-11
【基金项目】国家自然科学基金项目(51264018,51064012)。
【中图分类号】TQ172.79
【文献标识码】A
【文章编号】1007-9386(2015)06-0053-05

