基于子集模拟优化的空天飞机再入轨迹混合优化方法

朱俊杰 余雄庆

1.飞行器先进设计技术国防重点学科实验室，南京210016

2.南京航空航天大学，南京210016

空天飞机轨迹优化是在飞行动力学和物理学约束的条件下，寻求某种意义下最优解的过程，它贯穿于整个飞行器设计过程中，影响着总体、气动布局、制导控制、动力和结构等多个分系统的设计。

轨迹优化是一类最优控制问题，属于复杂的大规模非线性优化范畴。轨迹优化设计方法主要有基于极大值原理的间接法和基于非线性规划理论的直接法。间接法的优点是计算精度高，且能满足最优必要性条件，但由于繁杂的数学推导和难于求解的两点边值问题，目前已很少使用间接法求解轨迹优化问题。随着计算机技术的发展，目前的研究更多倾向于使用直接法求解。采用直接法求解轨迹优化问题时，先将最优控制问题转化为非线性规划问题(nonlinear programming，NLP)，对控制变量和状态变量进行离散，对状态方程、端点约束以及路径约束进行节点转化，再选择优化算法求解决策向量和目标函数［1］。

优化算法一般可分为2类:1)经典优化算法，例如序列二次规划法(简称SQP)，梯度下降法和罚函数方法［2］等;2)智能优化算法，例如遗传算法(Genetic Algorithm，简称GA)，进化策略(Evolution Strategy，简称ES)和粒子群优化(Particle Swarm Optimization，简称PSO)［3］等。基于梯度的优化算法的优点是收敛速度快，但对初值较为敏感，且容易陷入局部最优点。对于空天飞机再入轨迹问题，有数百甚至数千个设计变量，面对这么多变量，以人工方式给出一个合理的初始值，几乎不可能。智能优化算法的优点是无需给出初值，稳健性好，但收敛速度慢，优化结果不够精确。为了克服经典优化算法和智能优化算法的缺点，近年来，有学者将GA与SQP相结合来求解轨迹优化问题，如Vavrina采用GA与梯度迭代算法相结合的方法求解低推力轨迹优化问题［4］。但是，用GA-SQP混合算法求解再入轨迹优化问题时，通常选取的配点数为30～50［1］，配点数继续增加的话，GA为SQP提供的初始点的质量会越来越差，导致SQP最终不易收敛。而在某些轨迹优化问题中，取30～50个配点可能精度上不能满足设计要求。

本文尝试采用一种新的随机优化算法-子集模拟优化算法［5］(Subset Simulation Optimization，简称SSO)，来改进现有的混合优化方法，这种方法简称为SSO-SQP。有关研究表明:SSO与GA相比，具有更快的收敛速度［6］。本文以典型空天飞机再入轨迹混合优化问题为算例，测试SSO-SQP的有效性。

1 再入轨迹优化问题的描述

1.1 运动方程及设计变量

飞行器再入大气层时的三自由度运动学和动力学方程组如下［7］:

式中:m为空天飞机质量(kg)，R为飞行器质心到地心的距离(m)，Φ为经度(rad)，θ为纬度(rad)，v为速度(m/s)，γ为航迹角(rad)，ψ为航迹方向角(rad)，α为迎角(rad)，β为倾侧角(rad)，D为阻力，L为升力，g为不同高度的重力加速度。定义x=［R，Φ ，θ，v，γ，ψ］为状态变量，u=［α，β］为控制变量，设计变量包括状态变量和控制变量。D和L由下式确定:

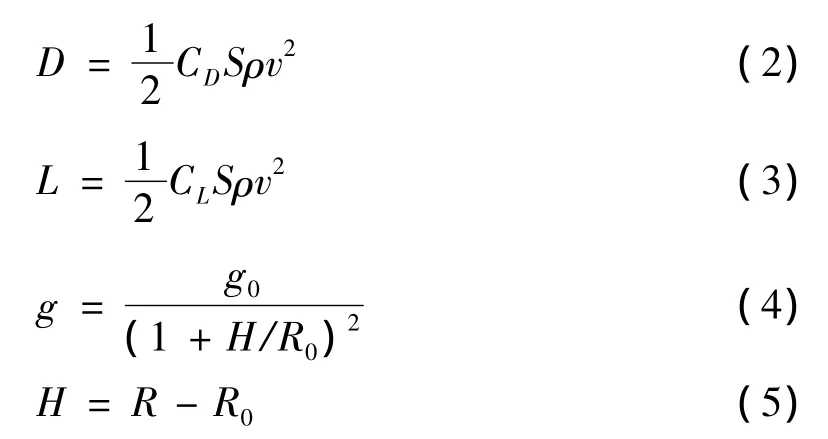
式中:g0为地球表面的重力加速度，大小为9.8m/s2;H为空天飞机离地面高度;R0为地球半径，大小为6357km;S为空天飞机参考面积;CD和CL分别为阻力系数与升力系数。

在大气飞行过程的热流密度为:

1.2 归一化处理

对于再入轨迹优化问题，不同变量之间的数值量级相差较大，例如R是106级别，而经度和纬度化为弧度后是1～10级别，两者数值上相差太大，会导致数值奇异，优化计算失败。为了增加优化计算的稳健性，需要对原始模型归一化处理。令:

1.3 优化目标

优化目标的选择主要由空天飞机的设计及任务要求确定，通常有如下4种优化目标:1)以飞行航程最大作为性能指标;2)以再入过程中总吸热量最小作为性能指标［9］;3)以最小能量消耗作为性能指标［10］;4)以到达指定目标点飞行时间最短作为性能指标。

1.4 约束条件

再入轨迹优化中的约束包括终端约束、路径约束、动压及热流峰值约束、过载约束和控制量约束［9］等。

2 SSO-SQP混合优化方法

SSO-SQP混合优化方法的思路是:首先在整个设计空间使用SSO算法进行全局搜索，迭代适当步数。待SSO迭代终止后，将SSO计算结果作为SQP优化算法的初始点，使用SNOPT软件包进行再次优化，得出收敛后的结果。以下对SSO和SQP算法进行简要介绍。

2.1 SSO算法

子集模拟优化算法的基本思想是极值问题(优化问题)，可以看作小失效概率问题(可靠性问题)［5］。在进行转换时，首先考虑如下无约束单目标全局优化问题:

其中f:Rn→Ω是一个实值函数，x是设计变量并且Ω是一个封闭有边界的集合。全局最小值fopt为满足下式的解xopt:

为了在可靠性分析框架中研究优化问题，人为设定设计变量为随机变量，这个“随机化”处理使得目标函数f也变为一个随机变量，且拥有自己的概率密度函数和累积分布函数。根据累积分布函数的数学定义可知，累积分布函数曲线是单调非减，并且右连续，有且仅有唯一的最小值fopt。构造一个可靠性问题如下:

其中，失效事件为F={f(x)≤fopt}。显然，与方程(14)有关的失效概率是0，因为fopt是全局最小。然而所关心的不是这个失效概率，而是目标函数最小值点或者包含目标函数最小值的区域。失效事件的变量区域与函数取得最小值的变量区域是对应的，从而实现了最优化问题向可靠性问题的转化，进而可用子集模拟方法解决优化问题［6］。

SSO算法的计算步骤［5］如下:

首先，定义一个约束违反函数用于处理约束条件并将样本排序。对于一个不等式约束条件，gi(x)≤0对应约束违反函数定义为

2)根据人工分布类型，利用直接的Monte Carlo模拟来生成 N个独立同分布的样本{x1，x2，…，xN}。计算所有随机样本的目标函数值，并将其用双标准排序方法升序排列，即有{W1，l:l=1，…，N}。此处，下标“1”表示这些目标函数的值对应于第1层模拟。设定xN为当前序列中的最佳求解方案，而x1为最差求解方案。合理选取p1和N，使得N(1-p1)为整数，从唯一序列中得到第N(1-p1)个样本xN(1-p1)以及相应的W1，N(1-p1)和Fcon(xN(1-p1))。选取第1组中间事件的临界值为:W1=W1，N(1-p1)以及 Fc1=F(xN(1-p1))。其中，下标“1”表示第1层模拟，则第1个中间事件F1定义为:

中间事件F1的定义也是满足双标准排序准则的，以约束条件优先。分开考虑{Fc1=0}和{Fc1＜0}两种情况，容易得到P(F1)的估计值为p1。无论何种情况，总有p1N个样本属于F1，为下一层模拟生成新样本提供“种子”样本。

3)采用改进的Metropolis-Hasting算法从中间事件中生成条件样本［5］。在第k层模拟中，从Fk-1中每个样本开始，可以生成相同分布的Markov链。再一次计算全局约束函数值和目标函数值，对该层内的所有随机样本进行双标准排序，确定序列中第N(1-pk)个样本xN(1-pk)。然后根据Fk选择样本，Fk定义如下:

2.2 SQP算法

SQP法的思想是通过一系列二次规划(QP)子问题来求解非线性问题。SQP的基本结构包括主迭代和次迭代，主迭代逐渐收敛于问题的最优解，主迭代中的QP子问题产生下次主迭代的搜索方向。QP子问题本身是一个迭代过程，即SQP的次迭代是QP子问题迭代。本文的SQP算法来源于SNOPT程序［11］。SNOPT程序采用了一种改进的序列二次规划算法(SQP)，适用于求解大规模非线性稀疏的优化问题。

3 算例

空天飞机再入轨迹优化算例取自文献［12］，并在该算例基础上增加了热流密度约束、动压约束和过载约束。

飞行器的气动模型如下:

空天飞机参考面积S=250.237m2，质量m=92162kg，前缘半径RN=1m。不同高度下大气参数参见文献［13］。

本例的设计变量包括状态变量和控制变量。x=［R，Φ ，θ，v，γ，ψ］为状态变量，u=［α，β］为控制变量。该优化问题的初始状态是:

优化目标是通过控制迎角α和倾侧角β，使航程最大，对于本例来说，与纬度最大等价。本例以纬度最大为最优目标:J=maxθ(tf)。在本例中SSO算法的参数设定为:单层样本量取100，条件概率取0.51，最大层数取100，终止精度取10-6。离散方法采用Hermite-Simpson法。

为了验证SSO-SQP算法的鲁棒性，计算了不同配点数情况下的轨迹优化问题。计算机配置为3.10GHz，内存2GB。SSO迭代100步，7s内就能计算完毕。最终结果见表1。

表1 不同配点数的SSO-SQP优化结果

由表1可见:1)随着配点数的增加，优化结果少量增加，但是当配点数增加到160时，最优值基本不变了;2)随着配点数的增加，SQP迭代步数和优化时间也逐渐增加，当配点数增加到160时，SQP迭代步数和优化时间开始大幅度增加，所以在优化计算时，配点数可以选在100～140之间，这样精度上既能满足要求，又相对节省计算时间。

当配点数为140时，迎角和倾侧角随时间变化曲线如图1和2所示。热流密度、动压和过载曲线如图3～5所示，可以看出优化结果能很好地满足约束要求。

图1 迎角随时间的变化

图2 倾侧角随时间的变化

图3 热流密度随时间的变化

图4 动压随时间的变化

图5 过载随时间的变化

4 结论

提出了一种SSO-SQP混合优化方法来求解空天飞机再入轨迹优化问题。SSO算法属于随机优化算法，不需要初始值，鲁棒性强。算例证明，仅需迭代100步(7s内就能计算完毕)就能获得一个较好的初始值，因此用SSO作为获得SQP算法初始值的手段是有效的。在SSO给出了合理初始值后，利用SQP算法收敛速度快、精度高的优点，能高效地寻到最优轨迹。算例表明:

1)该算法能有效地求解空天飞机轨迹优化问题，能根据精度和计算时间要求，设定配点数;

2)SSO-SQP算法鲁棒性较强，当配点从20增加到180时，均能优化出正确结果;

3)通常情况下，选择配点数为100～140，算例的设计变量数为809～1129，约束方程有903～1263个。经SSO优化得到初始值后，SQP仅需迭代300步左右就能收敛，可见该混合算法优化效率较高。

［1］ 张鼎逆，刘毅.基于改进遗传算法和序列二次规划的再入轨迹优化［J］.浙江大学学报(工学版)，2014，48(1):161-167.(Zhang Dingni，Liu Yi.Reentry trajectory optimization based on improved genetic algorithm and sequential quadratic programming［J］.Journal of Zhejiang University(Engineering Science)，2014，48(1):161-167.)

［2］ 陈功，傅瑜，郭继峰.飞行器轨迹优化方法综述［J］.飞行力学，2011，29(4):1-5.(Chen Gong，Fu Yu，Guo JiFeng.Survey of aircraft trajectory optimization methods［J］.Flight Dynamics，2011，29(4):1-5.)

［3］ 杨希祥，李晓斌，肖飞，等.智能优化算法及其在飞行器优化设计领域的应用综述［J］.宇航学报，2009，30(6):2051-2061.(Yang Xixiang，Li Xiaobin，Xiao Fei，et al.Overview of intelligent optimization algorithm and its application in flight vehicles optimization design［J］.Journal of Astronautics，2009，30(6):2051-2061.)

［4］ Vavrina M A，Howell K C.Global low-thrust trajectory optimization through hybridization of a genetic algorithm and a direct method［C］//AIAA/AAS Astrodynamics Specialist Conference and Exhibit.Honolulu:［s.n.］，2008:1-27.

［5］ 李红双，马远卓.结构可靠性分析与随机优化设计的统一方法［M］.北京:国防工业出版社，2015:223-260.(Li Hongshuang，Ma Zhuoyuan.Unified Methods for Structual Reliability Analysis and Stochastic Optimization Design［M］.Beijing:National Defense industry press，2015:223-260.)

［6］ Li H S，Au S K.Design optimization using subset simulation algorithm［J］.Structural Safety，2010，32(6):384-392.

［7］ Rahimi A，Kumar K D，Alighanbari H.Particle swarm optimization applied to spacecraft reentry trajectory［J］.Journal of Guidance，Control，and Dynamics，2013，36(1):307-310.

［8］ 雍恩米，唐国金，陈磊.基于Gauss伪谱方法的高超声速飞行器再入轨迹快速优化［J］.宇航学报，2008，29(6):1766-1772.(Yong Enmi，Tang Guojin，Chen Lei.Rapid trajectory optimization for hypersonic reentry vehicle［J］.Journal of Astronautics，2008，29(6):1766-1772.)

［9］ 汤亮，杨建民，陈风雨.多约束条件下的升力滑翔式再入轨迹优化［J］.导弹与航天运载技术，2013(1):1-5.(Tang Liang，Yang Jianmin，Chen Fengyu.Trajectory optimization with multi-constraints for a lifting reentry vehicle［J］.Missiles and Space Vehicles，2013(1):1-5.)

［10］ 陈刚，万自明，徐敏，等.飞行器轨迹优化应用遗传算法的参数化与约束处理方法研究［J］.系统仿真学报，2005，17(11):2737-2740.(Chen Gang，Wan Ziming，Xu min，et al.Parameterization method and constraints transformation method for RLV reentry trajectory optimization using genetic algorithm［J］.Journal of System Simulation，2005，17(11):2737-2740.)

［11］ Gill P E，Murray W，Saunders M A.User's Guide for SNOPT Version 7:Software for Large-Scale Nonlinear Programming［R］.Department of Mathematics University of California，San Diego.2010.06.16.

［12］ Zondervan K P，Bauer T P，Betts J T，Huff-man W P.Solving the Optimal Control Problem Using a Nonlinear Programming Technique Part 3:Optimal Shuttle Reentry Trajectories［C］.AIAA-84-2039.

［13］ 杨炳尉.标准大气参数的公式表示［J］.宇航学报，1983，(1):83-86.(Yang Bingwei.Formulization of standard atmospheric parameters［J］.Journal of Astronautics，1983，(1):83-86.)